浅析待定系数法在绝对值问题中的应用

陈少春

浙江省绍兴鲁迅中学 (312000)

浅析待定系数法在绝对值问题中的应用

陈少春

浙江省绍兴鲁迅中学 (312000)

二次函数的绝对值问题一直受高考命题者的青睐，缘由是它既是我们比较熟悉的知识内容，但又能考查我们的综合分析问题的能力．如何破解这类问题？本文想尝试“待定系数法”的方法解决二次函数的绝对值问题中的“证明、最值、范围”，希望给我们考生在解决此类问题带来些许帮助．

一、二次函数绝对值的“证明”问题

例1 二次函数f(x)=ax2+bx+c，当|x|≤1时，|f(x)|≤1.求证：当|x|≤2时，|f(x)|≤7．

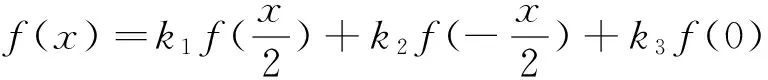
注：该例可推广到更一般的情形.

二次函数f(x)=ax2+bx+c，当|x|≤1时，|f(x)|≤1．求证：当|x|≤n时，|f(x)|≤2n2-1(n∈N*)．

例2 已知函数f(x)=x2+ax+b．

(1)设b=a，若|f(x)|在x∈[0,1]上单调递增，求实数a的取值范围；

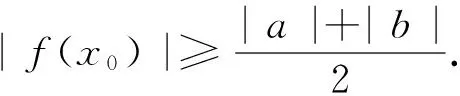
解：(1)略；

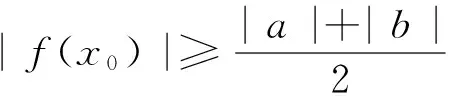
二、二次函数绝对值的“最值”问题

在各地模拟卷里我们经常碰到这样的问题：求一个带多个参数的绝对值二次函数在某个区间上最大值的最小值，解决这种常规方法是分类讨论和数形结合来解决，但是因为参数太多，很多同学无从下手．其实通过图形分析可以发现，这类问题最小值一定是在两个端点和对称轴的函数值相等取到的，为待定系数法解决这类问题提供了思路．

类型1f(x)=|ax2+bx+c|(a为常数)型最小值

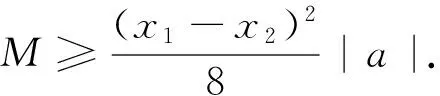
例3 (2016年嘉兴期末理18)已知函数f(x)=x2+2bx+c，设函数g(x)=|f(x)|在区间[-1,1]上的最大值为M．

(1)若b=2，试求出M；

(2)若M≥k对任意的b，c恒成立，试求出k的最大值．

解：(1)略；

例4 (2016年稽阳联考理18)已知二次函数f(x)=-x2+ax+b(a,b∈R)，设M(a,b)是函数g(x)=|f(x)|在[1,2]上的最大值．

(1)当a=1时，求M(1,b)关于b的解析式；

由于大型渠道混凝土衬砌施工作业多在1∶2或更陡的坡面上进行切缝施工，且自动行走，能使其平稳地行驶在坡面上，配重调整过重过轻、配重的位置都是影响实际应用的主要因素，所以机具的配重尤为重要。

(2)若对任意的a,b∈R，恒有M(a,b)≥M(a0,b0)，求所有满足条件的实数对(a0,b0)．

解：(1)略；

类型2f(x)=|ax2+bx+c|(b为常数)型最小值

结论f(x)=|ax2+bx+c|(b为常数)在区间[x1,x2]上的最大值是M，则

(1)当a=0，b=1时，写出函数f(x)的单调区间；

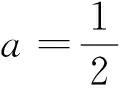
(3)若对任意实数a,b，总存在实数x0∈[0,4]使得不等式f(x0)≥m成立，求实数m的取值范围.

解：(1)、(2)略；

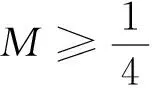
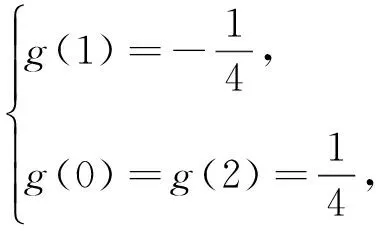
类型3f(x)=|ax2+bx+c|(b为参数且动区间)型最小值

这类问题可以通过变量换元使得区间变成定区间，从而把问题转化成类型1或者类型2.

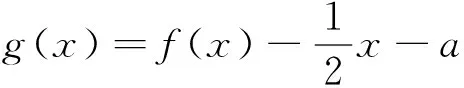
(2)记M(a,t)为函数f(x)在区间[t,t+2]上的最大值(t∈R)，求M(a,t)的最小值.

解：(1)略；

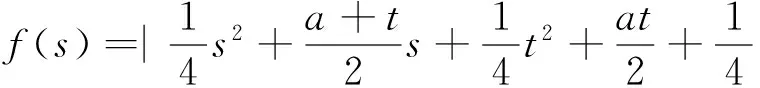
三、二次函数绝对值的“范围”问题

例7 已知函数f(x)=ax2-c，满足|f(1)|≤1,|f(2)|≤5，求f(3)的范围．