“直观感知”助你轻松求解几道数列题

吴丽琴

福建省漳州第一中学 (363000)

“直观感知”助你轻松求解几道数列题

吴丽琴

福建省漳州第一中学 (363000)

数列作为高中数学的一个重要组成部分，是历届高考试题考查的重点，也是难点．高考数列试题常与不等式、函数、方程等知识交汇在一起综合命制，对学生能力提出了较高的要求，要求学生具有较好的数学素养，较好地突出高考试题的甄别功能．正是如此，使得该类试题常成为考生高考高分路上的拦路虎，时常困扰着广大考生．那么，如何破解这类问题呢？我们知道表示数列的方法通常有图像法、列举法、通项公式an=f(n)、递推关系等，其中，递推关系最抽象，通项公式次之.高考数列试题中数列的表示往往以抽象的形式出现(一般给出其递推关系、通项公式)，如果能够将其具体化、直观化(列举法、图像法)，这有助于知道问题的来龙去脉，有助于形成正确的猜想，确立解题的思路[1]．

例1 ((2012年新课标Ⅰ，理科))数列{an}满足an+1+(-1)nan=2n-1，则{an}的前60项和为________.

例2 (2014年新课标Ⅰ理)已知数列{an}的前n项和为Sn，a1=1，an≠0，anan+1=λSn-1，其中λ为常数．

(1)证明：an+2-an=λ；

(2)是否存在λ，使得{an}为等差数列？并说明理由．

分析与解：(1)略；(2)由(1)及已知条件得出数列各项为，1，λ-1，λ+1，2λ-1，…，若{an}为等差数列，则2(λ-1)=1+λ+1，解得λ=4；当λ=4时，数列各项为1，3，5，7，…，猜想{an}为等差数列，且公差为2．下面用数学归纳法证明：当λ=4时，an+1-an=2，n∈N*．

当λ=4时，①a2-a1=3-1=2，所以n=1时，等式成立；②假设ak+1-ak=2，∀k∈N*，则由(1)及假设得，ak+2-ak+1=ak+4-ak+1=4-2=2，所以n=k+1时，等式也成立；由①②可知该等式成立．

例3 (2017年福建省高三毕业班单科质检，第12题)已知数列{an}，{bn}满足a1=b1=1，an+1=an+2bn，bn+1=an+bn，则下列结论正确的是( ).

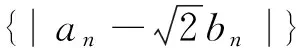
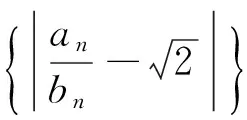
分析与解：由已知条件列出{an}、{bn}的前5项，画出如下表格.

n12345…an1371741…bn1251229…

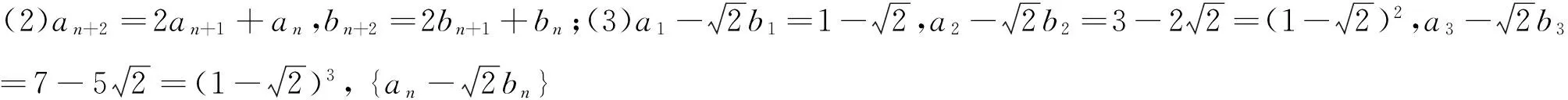
例4 (2015年陕西省理科第21题)设fn(x)是等比数列1，x，x2，…，xn的各项和，其中x>0，n∈N，n≥2．

(2)设有一个与上述等比数列的首项、末项、项数分别相同的等差数列，其各项和为gn(x)，比较fn(x)和gn(x)的大小，并加以证明．

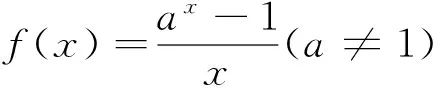
(1)求f(x)的单调区间；

(2)若f(x)的最小值为0，回答下列问题：

(ⅰ)求实数a的值；

(ⅱ)已知数列{an}满足a1=1，an+1=f(an)+2，记[x]表示不大于x的最大整数Sn=[a1]+[a2]+…+[an]，求Sn．

分析与解：(1)略；(2)(ⅰ)a=1；

图1

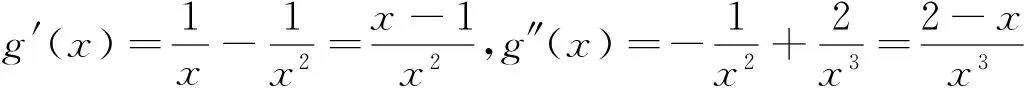
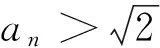
下面证明：{an}是单调递增，且当n≥2，n∈N时，2≤an

(1)先证明当n≥2，n∈N时，2≤an

(ⅰ)当n=2时，a2=2∈[2,x0)，所以n=2时，不等式成立；

由上面几道数列试题的解题过程，我们可以看出，若能将数列的项具体化、直观化，则能帮助我们从不同视角理解题意，明确这道题的解题方向，因为解题思路的产生更多的源于直觉，源于我们对这道题目的直观判断，除非它是常规的题型，预期这道题的最终结果．直觉意义往往可以超越逻辑步骤，捷足先登的直达目标，但具体到解答步骤，还是要回到数学的抽象表达，运用严密的数学推理[1]．

[1]裴光亚．从试题的直观意义上获取解题思路[J]．数学通讯，2003年第10期.