真空疏干降水与地表变形控制数值模拟研究

张冬冬，陈龙珠，孙瑞瑞(.上海交通大学船建学院安全与防灾工程研究所，上海 0040；.上海市地矿工程勘察院，上海 0007)



真空疏干降水与地表变形控制数值模拟研究

张冬冬1，陈龙珠1，孙瑞瑞2
(1.上海交通大学船建学院安全与防灾工程研究所，上海 200240；2.上海市地矿工程勘察院，上海 200072)

0 引言

近年来，城市地下空间建设越来越受重视，长三角地区地下水位埋深较浅，地铁站建设大多要采取工程降水措施.在低渗透地基中常规采用真空疏干降水方法降低基坑水位，工程降水引起地表变形不可避免，如何采取有效的围护措施减小地表变形显得尤为重要.目前对地下水问题的研究，国内学者常采取现场试验和数值模拟的方式，数值计算的成果也很多，尤其长三角地区研究成果也很多.针对基坑降水问题，对基坑减压降水国内学者也有诸多研究，张冬冬[1-4]针对工程实例针对抽水试验数据建立数学模型，对地下水渗流和地表变形进行趋势预测.Wu Yongxia等[5-6]对地下水与地表变形性状进行研究.Wang[7]等对上海轨道交通9号线宜山路站对承压含水层进行数值计算，对有限控制周边环境起到了很好的效果.骆祖江[8]，Dassargues[9]等对上海第四纪松散沉积层地下水渗流与地表变形控制进行研究.吴林高[10]等对地下水渗流与工程实践结合，解决很多地下水问题.周念清[11-12]等以徐家汇地铁站为例，根据工程条件建立地下水渗流模型，利用现场试验反演参数并建立数值模型，对地表变形进行预测控制，取得很好效果.在基坑渗流数值模拟计算方面，吴林高[1]、骆祖江[2]、Shen S L[3]、许烨霜[4]、Wu Yongxia[5-6]等人将渗流理论与工程实践结合，解决了众多的工程地下水问题；周念清[7-8]、张冬冬[9-13]针对工程实例针对承压水进行抽水试验数据建立数学模型，对地下水渗流和地表变形进行趋势预测.孙瑞瑞[14]针对软土地基中基坑渗透破坏机理和对策进行研究.其他国内外学者[15-18]也针对具体工程成功应用数值方法进行分析.本文中以宁波轨道交通樱花公园站基坑降水为例进行数值计算，结合现场试验数据进行模型拟合预测，考虑真空度为0.8 MPa，对有无围护结构的两种工况计算，对基坑降水引起的地表沉降进行预测，并分析讨论渗透系数和井深在地基中的影响，为地铁基坑降水设计施工提供指导作用.

1 工程概况

1.1 工程背景 宁波轨道交通樱花公园站位于中山东路与中兴路，车站结构型式、基坑开挖深度及施工方法见表1.地铁1号线与3号线在此交汇，站台呈“L”型相接换乘车站，如图1所示.

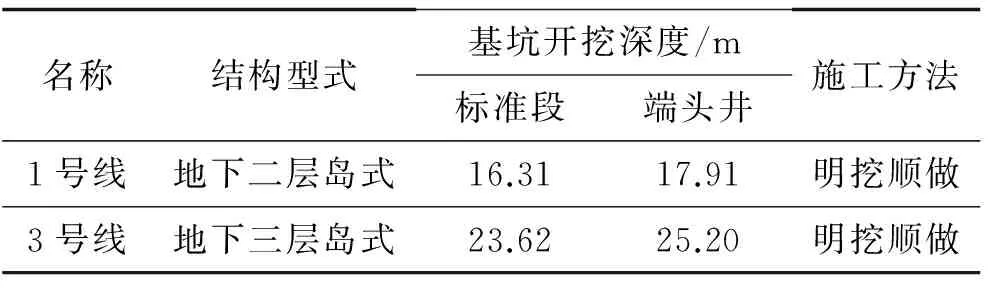
表1 基坑结构及施工方法

图1 基坑平面布置图

1号线中心里程为K13+848.130，主体结构总长为308.19 m，围护结构插入深度为32.90 m，主体东西向布置，西北侧为樱花公园，南侧紧邻中山东路.3号线中心里程为K18+105.000，主体结构总长为208.300 m，围护结构插入深度为47.50 m，西临樱花公园，北有后塘河，北端东侧枫丹公寓楼房，联络线近东航大厦4.40 m.地铁站周边环境复杂，地下管线分布密集、市区主干道路人车流繁忙，对周边环境的影响要求较高.

1.4 抽水试验 为确定场地的单井涌水量、静止水位、水位降深、影响半径等参数，进行抽水试验，当真空度为- 0.8 MPa时，单井涌水量测试结果为Q=0.14 m3/h，抽水38 h后水位观测和地表变形值见图4和图5.

2 数值模型的建立

2.1 基本思路 本计算中采用Geo-Studio软件进行平面流固耦合模拟，程序中把渗流模块SEEP/W计算的内容导入应力变形分析模块SIGMA/W，并作为应力变形分析时的孔隙水压力分布.

2.2 控制方程 假定流体密度不随时间而变化，且无源和汇情况下，根据质量守恒定律，以z为轴的轴对称柱坐标系中，土中水分运动的连续性方程为

(1)

式中，θ为体积含水量，对于饱和流，θ=n，n为土的孔隙率；qr、qφ、qz分别为相应于3个坐标方向上的水分运动通量.

2.3 地表变形 计算地下水位的下降就是土体的固结过程，从含水层抽水引起的固结作用导致地表变形.太沙基一维固结理论的基本微分方程为：

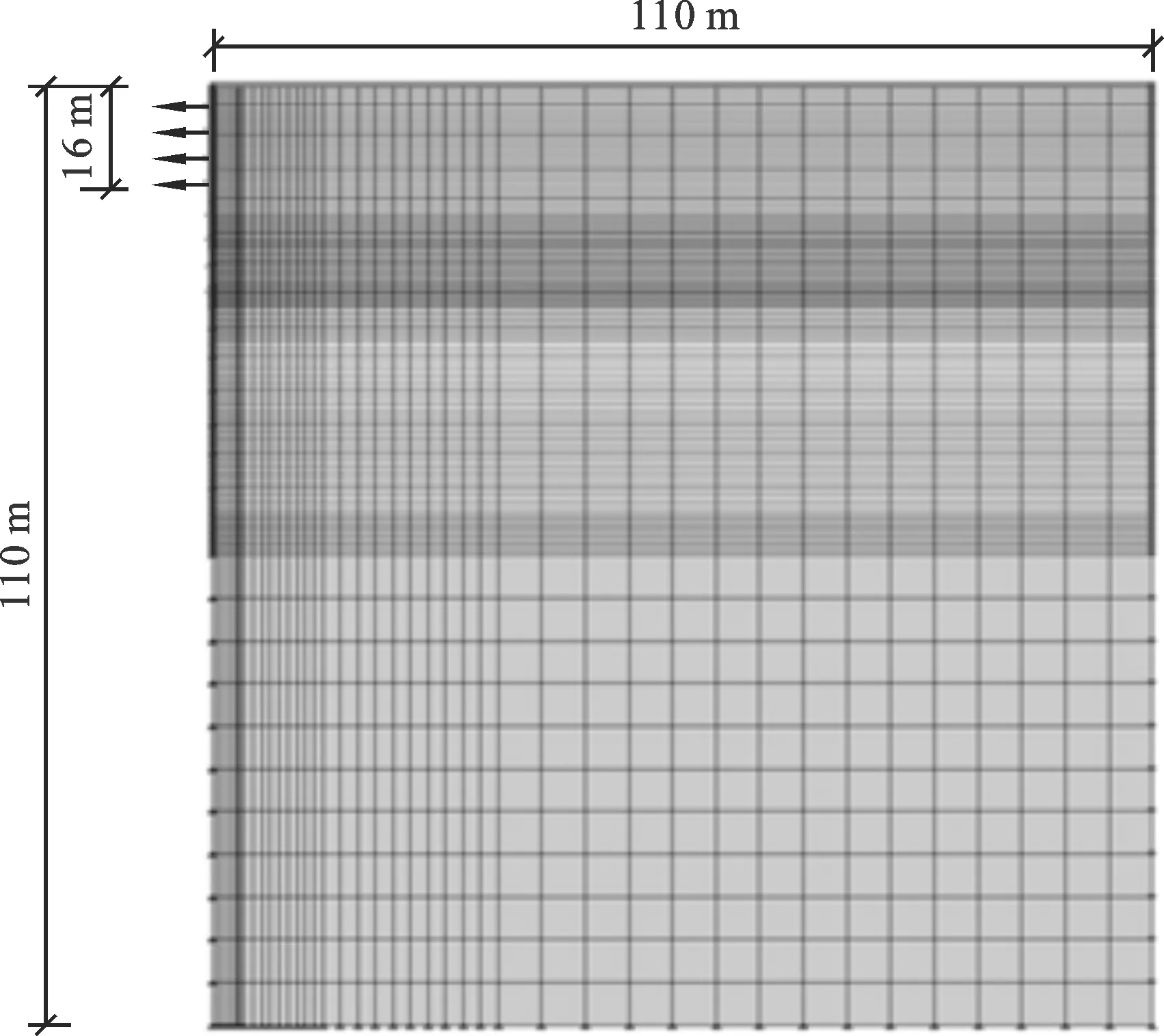
图2 试验井数值计算模型

(2)

压缩土层厚度为h时，土体的沉降量为：

(3)

2.4 模型的建立 图2为试验井数值计算模型.根据场区的实际水文地质结构条件及几何形状进行剖分.为消除地下水边界的影响，确定边界布置在降水井影响半径之外的原则，通过试算确定基坑中心点为基点，取110.00 m作为模拟计算区域，在平面尺寸上可满足模型计算精度要求.在垂向方向上，按照实际地质资料进行110.00 m深度划分.井深设置16.00 m，透水范围为12.00 m，单井涌水量按现场试验测试结果取Q=0.14 m3/h.井壁透水部位，施加孔压-0.8 MPa，计算时间取38 h.本数值模拟中仅考虑地基降水引起的地表沉降，不考虑周边施工引起的地表沉降.

3 模型验证与预测

3.1 模型的识别与验证 上述描述的数值模型需通过识别与验证后，方可用于模型预测，选取连续抽水38 h后地下水状态变化趋于稳定，对地下水位和地表沉降观测点进行拟合.图3和图4分别为连续抽水38 h地下水位和地表变形观测点拟合曲线，可见距井中心点2 m和6 m处，井内水位变化实测值分别为32 cm和18 cm，井内水位变化计算值分别为36 cm和15 cm，计算结果与现场实测结果较吻合，其他计算结果与现场实测结果也较吻合.地表沉降量较小，距井中心点5 m以上，地表沉降量均小于0.2 mm.因现场试验时，基坑周边正常施工，实测地表沉降值比计算值小.

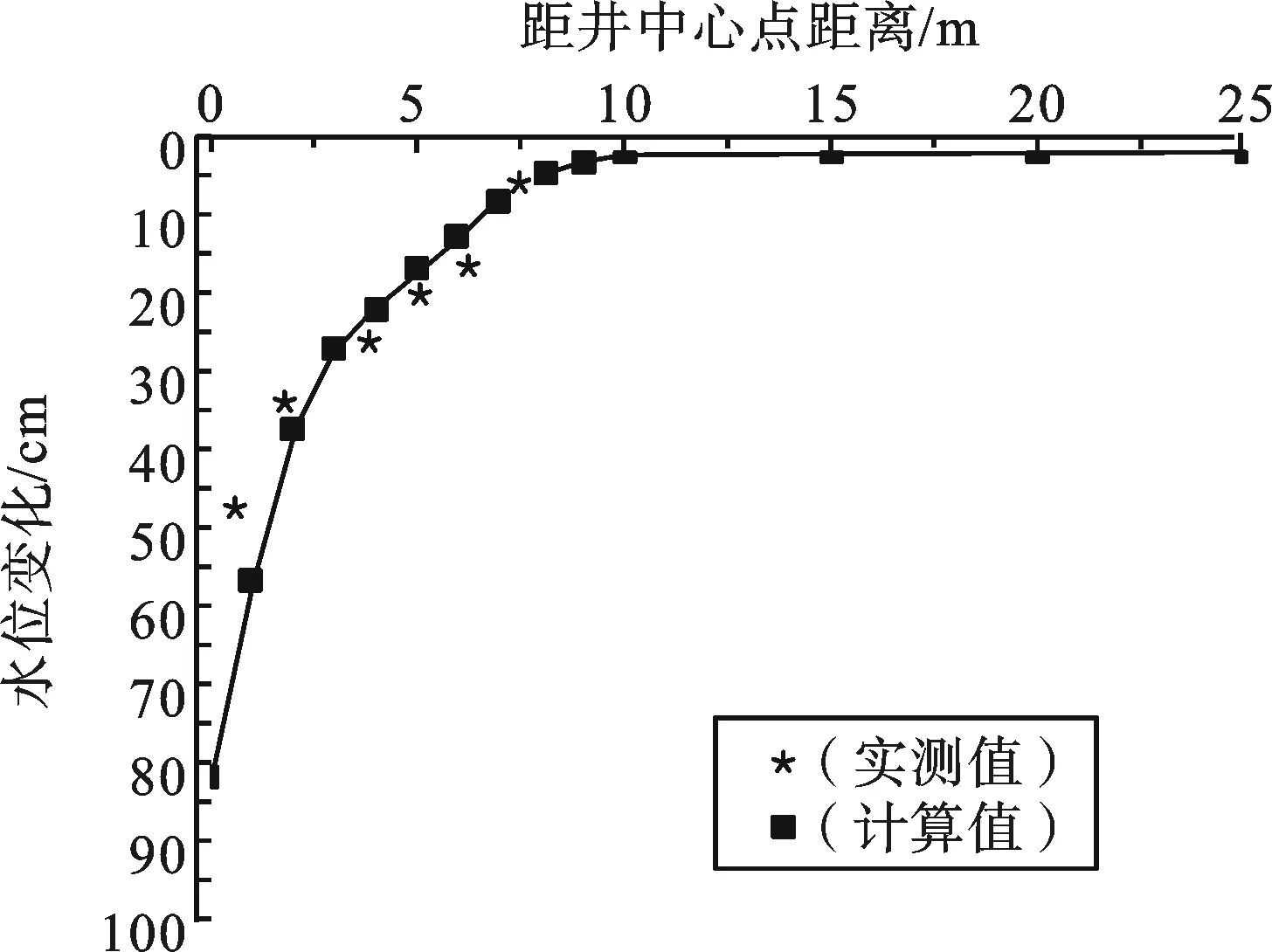
图3 连续抽水38 h地下水位观测点拟

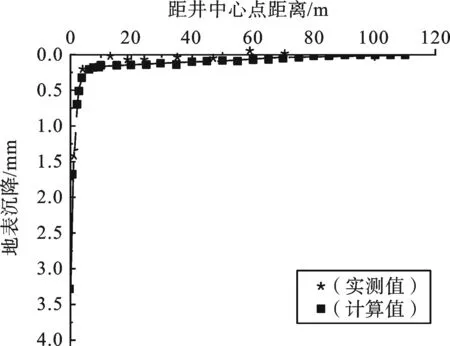
图4 连续抽水38 h地表沉降观测点拟

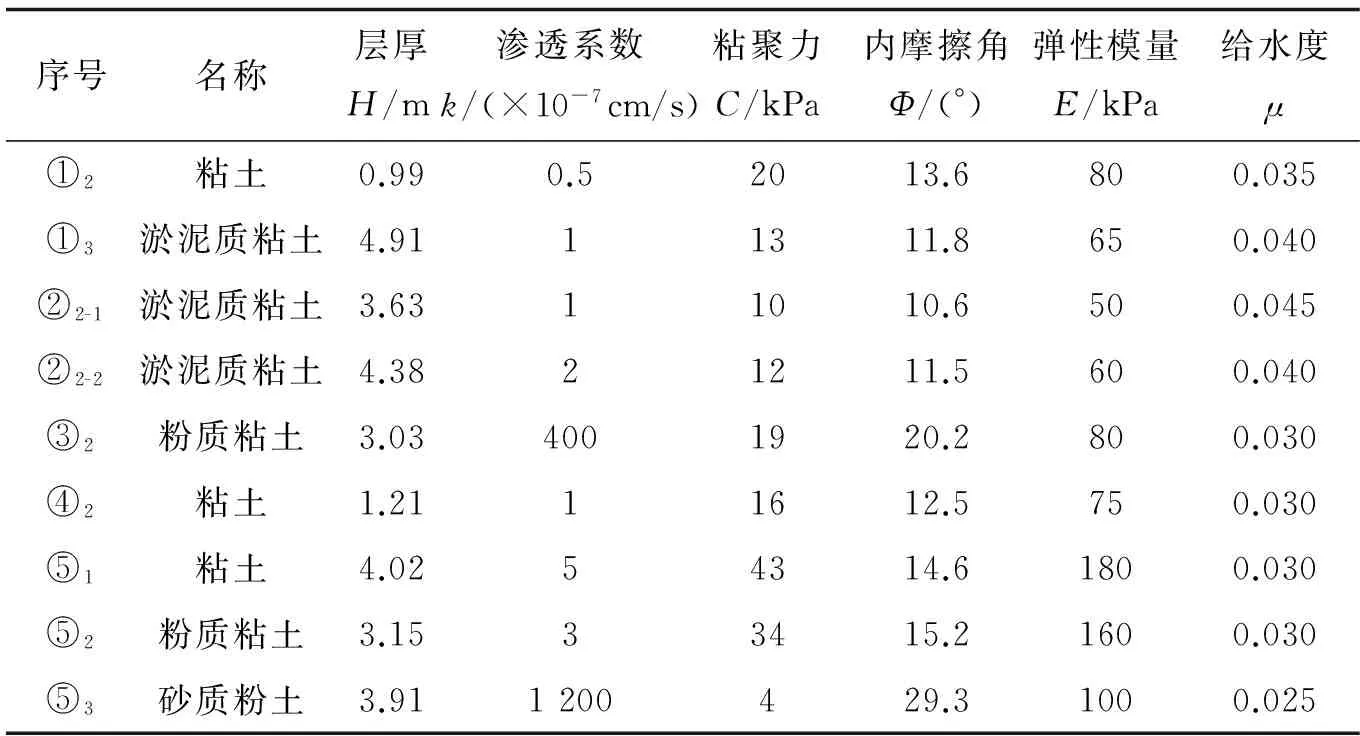
序号名称层厚H/m渗透系数k/(×10-7cm/s)粘聚力C/kPa内摩擦角Φ/(°)弹性模量E/kPa给水度μ①2粘土0.990.52013.6800.035①3淤泥质粘土4.9111311.8650.040②2-1淤泥质粘土3.6311010.6500.045②2-2淤泥质粘土4.3821211.5600.040③2粉质粘土3.034001920.2800.030④2粘土1.2111612.5750.030⑤1粘土4.0254314.61800.030⑤2粉质粘土3.1533415.21600.030⑤3砂质粉土3.911200429.31000.025

从图3和图4可看出地下水位和地表沉降的计算及实测值拟合程度较好，模型最终参数的确定也符合类似试验，因此该模型的识别具有一定精度和可信度，可以作为研究的计算依据.

通过对地下水位和地表沉降的拟合，不断调整模型参数，反演得出各土层的物理力学参数见表2. 表2为典型地质工程地质剖面数据表.

3.2 模型预测 根据建立的渗流数值计算模型，通过实测数据进行拟合效果较好，满足预测计算要求，然后进行数值模拟及地表变形计算.按照本场地地层分布及边界条件，选取井底位于②2-2淤泥质粘土层的15 m降水井，井底位于⑤1粘土层的22 m降水井，计算时考虑井内真空度为0.8 MPa，对有无围护结构的两种工况计算，分别进行抽水10 h、30 h、50 h和70 h的地表变形分析.

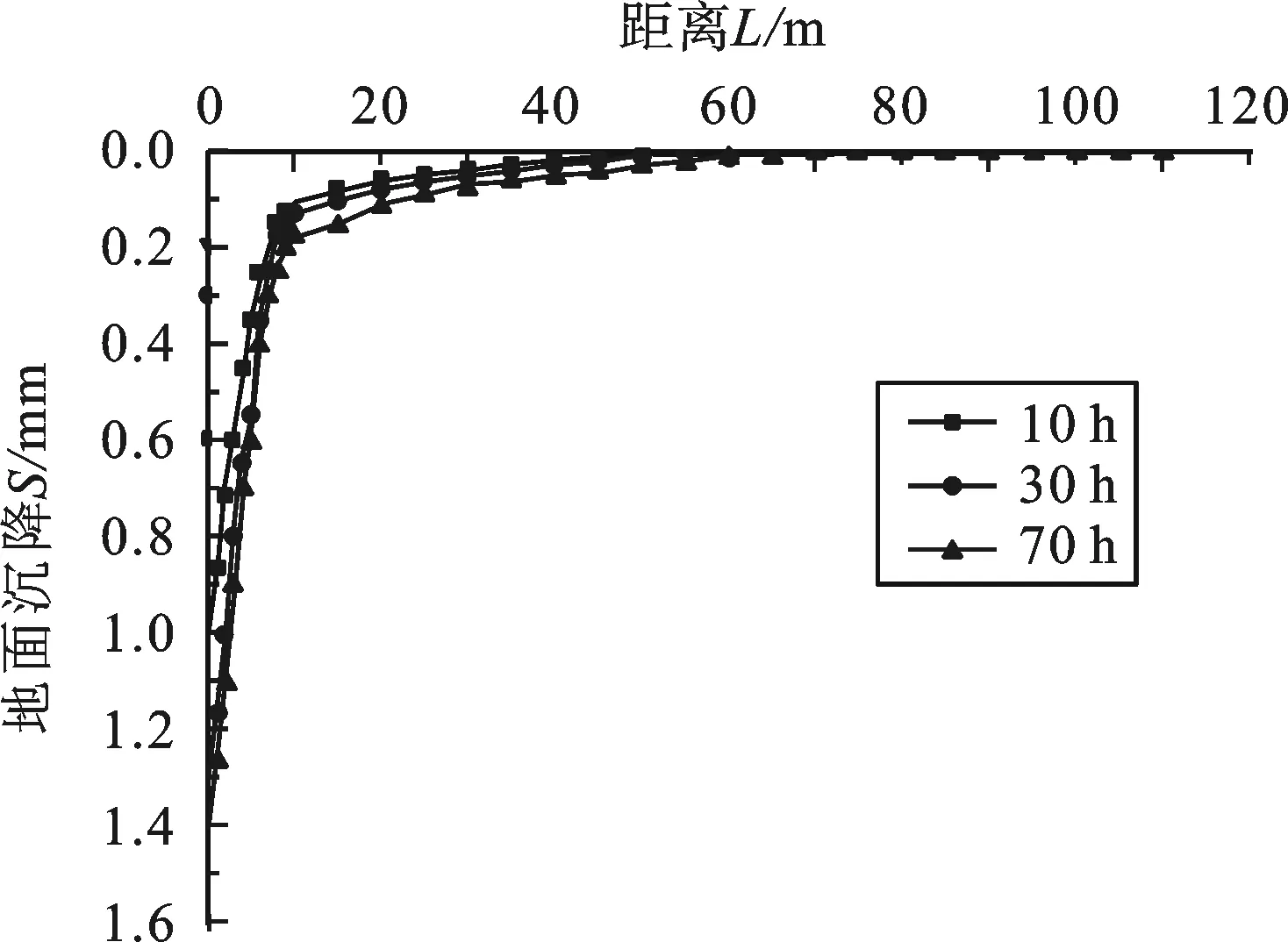
图5 无围护结构抽水引起的地表变形分布图

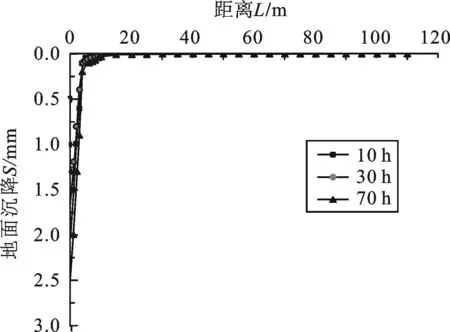
图6 有围护结构抽水引起的地表变形分布图

2) 22 m深疏干井.真空疏干降水引起的地表变形与围护结构的设置有密切关系，图7为无围护结构时，地表变形的影响范围可达60 m.图8为设置围护结构时，地表变形很小，对保护周边环境起到重要作用.围护结构对于降水引起的地表变形有积极作用.

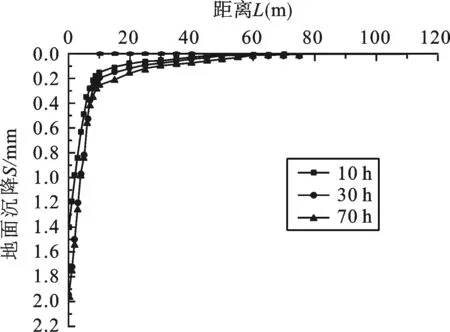
图7 无围护结构抽水引起的地表变形分布图

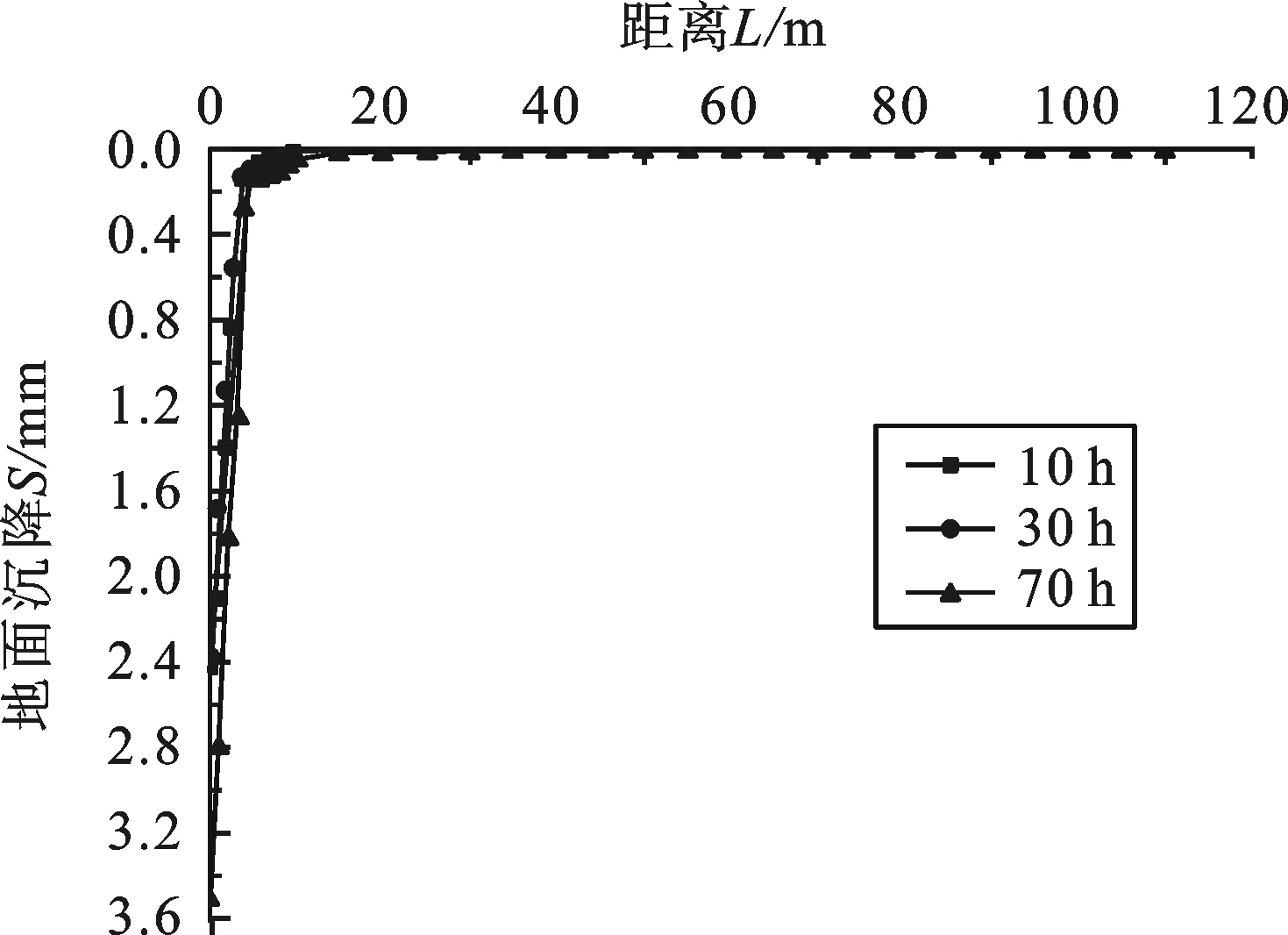
图8 有围护结构抽水引起的地表变形分布图

4 分析讨论

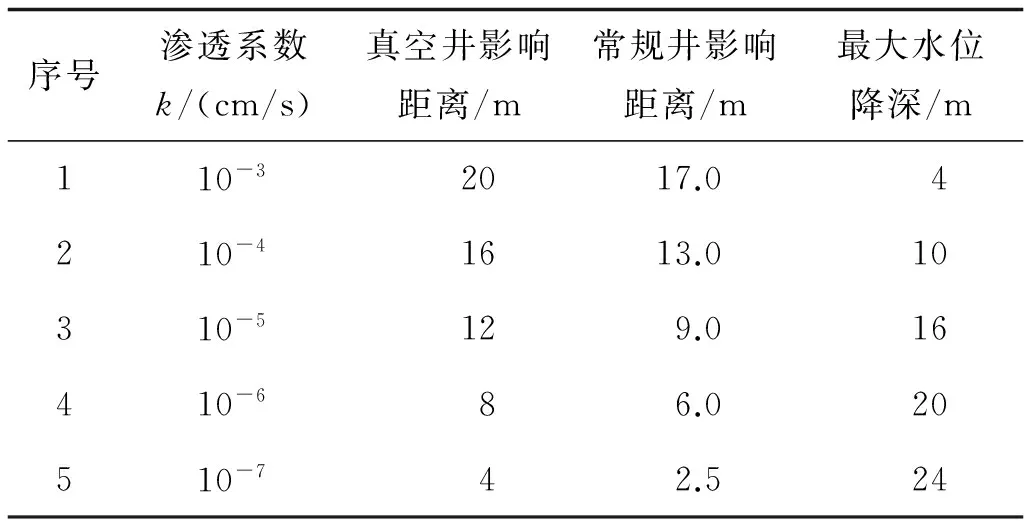
表3 渗透系数的影响分析

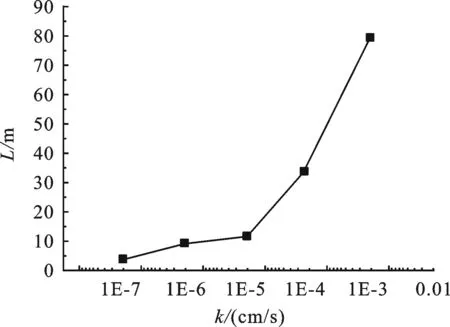
图9 水位下降的水平影响距离随渗透系数变

4.2 井深的影响分析 当土体渗透系数较低时，抽水对地下水位的影响范围较小，地基土渗透系数为k=10-7cm/s，10 m和16 m深井的地下水位下降的水平影响距离均为4.0 m.抽水流量不变的情况下，抽水井深度越大，地下水位下降的水平影响距离变化不大.因此，低渗透性地基中加大疏干井深度对地基降水的作用效果不明显.

5 结论

1) 真空疏干降水引起的地表变形与围护结构的设置有密切关系.无围护结构时，地表变形的影响范围和沉降量均明显大于有围护结构时.围护结构对于降水引起的地表变形有积极作用.

[1] 吴林高, 李国, 方兆昌, 等. 基坑工程降水案例[M]. 北京: 人民交通出版社, 2009.

[2] 骆祖江, 刘金宝, 李朗. 第四纪松散沉积层地下水疏降与地面沉降三维全耦合数值模拟[J]. 岩土工程学报, 2008,30(2): 193-198.

[3]Shen S L, Xu Y S. Numerical evaluation of land subsidence induced by groundwater pumping in shanghai[J]. Canadian Geotechnical Journal, 2011,48(9): 1378-1392.

[4] 许烨霜. 考虑地下构筑物对地下水渗流阻挡效应的地面沉降性状研究[D]. 上海：上海交通大学船舶海洋与建筑工程学院, 2009.

[5] Wu Yongxia, Shen Shuilong, Yin Zhenyu. Characteristics of groundwater seepage with cut-off wall in gravel aquifer I: field observations[J]. Canadian Geotechnical Journal, 2015, 52(10):1526-1538.

[6] Wu Yongxia, Shen Shuilong, Yin Zhenyu. Characteristics of groundwater seepage with cut-off wall in gravel aquifer II: numerical analysis[J]. Canadian Geotechnical Journal, 2015, 52(10):1539-1549.

[7] 周念清, 唐益群, 娄荣祥，等. 徐家汇地铁站深基坑降水数值模拟与沉降控制[J]. 岩土工程学报, 2011,33(12): 1950-1956.

[8] Zhou N Q, Vermeer P A, Lou R Q, et al. Numerical simulation of deep foundation pit dewatering and optimization of land subsidence controlling[J]. Engineering Geology, 2010, 116(3/4): 251-260.

[9] 张冬冬. 承压降水引起周边环境变形的数值模拟分析[J]. 上海地质, 2010, 31: 24-27.

[10] Zhang D D. Coupled numerical simulation research on dewatering and land subsidence in deep foundation pit[J]. Advanced Materials Research, 2013, 277:1549-1552.

[11] Zhang D D, Ding J W, Wang R B. Research on application of deep foundation pit decompression dewatering technology and impact on surrounding environment[J]. Advanced Materials Research, 2013, 671-674:101-104.

[12] 张卫国，肖长来，张冬冬. 深基坑工程降水技术设计和地面沉降控制措施[J]. 中国市政工程, 2011(5):55-58.

[13] Zhang D D, Zhou J F, Zhang W G, et al. The finite element analysis of the excavation on adjacent buildings based on mohr coulomb model[J]. Advanced Materials Research, 2011, 374-377:2171-2175.

[14] 孙瑞瑞. 软土地基中基坑渗透破坏机理和对策[J]. 上海地质, 2010,31:85-88.

[15] Wang J X, Hu L S, Wul G, et al. Hydraulic barrier function of the underground continuous concrete wall in the pit of metro station and its optimization[J]. Environmental Geology, 2009, 57: 447-453.

[16] Dassargues A, Biver P, Monjoie A. Geotechnical properties of the quaternary sediments in Shanghai[J]. Engineering Geology, 1991, 31:71-90.

[17] 张勇, 赵云云. 基坑降水引起地面沉降的实时预测[J]. 岩土力学, 2008, 29(6):1593-1596.

[18] 童立元, 刘松玉，郑灿政，等. 多功能孔压静力触探在基坑工程降水设计中的应用分析[J]. 岩土力学, 2015, 36(11): 3210-3216.

Numerical simulation of vacuum drying dewatering and control of surface deformation

ZHANG Dongdong1, CHEN Longzhu1, SUN Ruirui2

(1. Institute of Engineering Safety and Disaster Prevention, Ocean and Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China; 2. Shanghai Institute of Geological Engineering Exploration, Shanghai 200072, China)

Based on the monitoring data of groundwater and surface deformation about Ningbo Ying-hua park rail station of pumping test, using the Geo-Studio numerical model of fluid-solid coupling, we simulated to dewater of vacuum drying, which was prediction calculation the surface deformation of dewatering, quantitative analysis the influence of structure on surface deformation. Results show that the influence radius of vacuum wells is 1.2—1.5 times than conventional wells, as the effect of increasing the depth is not obvious, the support structure is effectively controlled the surrounding surface deformation.Key words: vacuum drying; numerical simulation; seepage head; surface deformation

2016-11-04

国家自然科学基金(51379122)资助

张冬冬(1984-)，男，博士生；陈龙珠，通信作者，教授，E-mail：mengdong02@163.com.

1000-2375(2017)03-0264-06

TU46

A

10.3969/j.issn.1000-2375.2017.03.010