课堂教学的慢艺术

周莹

[教学片段1]特异功能“慢”激趣

师：我练了一项特异功能，你们想不想知道？

师：从1开始连续奇数相加，我算得比计算器还快。想不想试试？

[赏析]开场，彭老师在告诉学生“特异功能”是什么后，开始了“人机大赛”。借着一个“太长了”的算式，学生对“用逐个相加的方法”计算的烦琐有了深刻的体会。放慢脚步，却在对话中拉近了师生之间的距离，还让学生切身体会到“特异功能”的妙处，有效地激发了学生进一步学习的欲望。

[教学片段2]数形联系“慢”感受

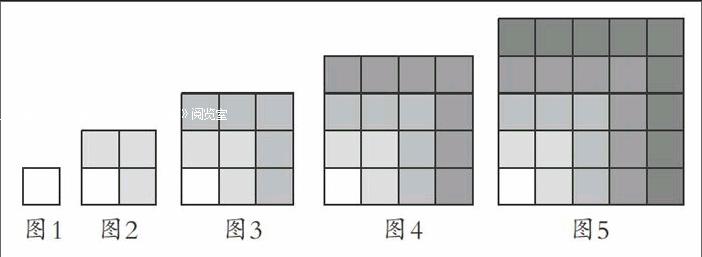
师展示图2-5：请你写出表示小正方形个数的算式。

师为每个小组下发一组图形：写出算式，计算你手上拿的那个图形的小正方形的个数。

师：怎么计算图中小正方形的个数？

生反馈：2乘2等于4个。2的平方。1+3。

师：1+3求的是什么？2求的又是什么？

生：都是求图中小正方形的数量。

师：这两个式子是？（相等的）

师：第二个图形。

生反馈：3²等于9。1+3+5=9。

师：这里的数表示？

生：l表示的是白色的小正方形，3表示蓝色的小方格，5表示红色的小正方形的数量。

生：有三层，每层三个，3乘3就是3²。

师：第三个图形的算式是什么？

生：1+3+5+7--42。

师：这里的数都表示什么？

生：1表示的是白色的小正方形，3表示蓝色的小方格，5表示红色的小正方格，7表示绿色的小正方形。

生.：我发现了老师的秘诀，那个算式就是16的平方，就是256。

师：他已经发现了我的秘诀了！刚刚我们研究了四个图形，我再补充一个（图1）。

师：它的算式怎么写？

生：1=1²。

师：我们观察一下，这些等式的左边和右边有什么规律？再结合图形来解释一下（分组讨论）。谁来汇报一下？

生：右边都是项数的平方。两个数就是2²，4个数就是4²，以此类推。

生：如果有n个加数就是n的平方。

生：左边是1+3，1和3的中间是2，右边就是22；左边1+3+5，它们的中间是3，右边就是3²？

师：观察一下，是不是都有这样的规律？

生：有的，1+3+5+7就是3和5中间是4，右边就是4²。

师：谁能结合图形来解释一下？需不需要讨论一下？小组讨论一下。

生：我还发现了一个规律，大正方形一行是几就是几的平方。

生：“1+3+5+7”这样四层小正方形，就刚好构成了一个4行4列的大正方形，所以1+3+5+7=4²。

师：猜一猜，第6个图形是什么样子的？

生反馈：1+3+5+7+9+11=6²。在黑板上最后一幅图外面再加一层。就是6行，每行有6个的一个大正方形。

师：第7个图形呢？

生反馈：在外层再加13个。1+3+5+7+9+11+13=7²。

师：刚刚看到，有的同学一边说一边在扳手指（教师模仿动作），这是在做什么？

生：在数加数的个数，第7幅图的左边应该有7个加数。

师：我的特异功能你们知道是什么了吗？如果100个连续奇数相加，得数是？

生：100的平方10000。

[赏析]彭老师放大了数形联系的过程，让学生用多种算式表示图形中小正方形的个数，建立“数与形”之间的链接：同时，从“求同一幅图中小正方形的数量”建立两种算式之间的对等关系，使学生清晰地感受到数与形的联系。以“左边和右边有什么规律？结合图形解释一下”这个问题为引，进一步引导学生以数形结合的方式考虑问题，实现数与形的相互印证。当学生一度出现困难时，彭老师没有急于登场，而是留给他们足够的时间，针对问题及时有效地组织学生再一次讨论交流，足见教者捕捉学生即时学习思维状态与灵活调控课堂的功力。

[教学片段3]以形助数“慢”运用

出示习题：

①1+3+5+7+5+3+1=（ ）

②1+3+5+7+9+1 1+13+1 1+9+7+5+3+1=（ ）

③（）=9²

师：题①的得数是多少？你是怎么想的？

生：25，先算1+3+5是9，再看后面是7，然后后面是5+3+1，其实就是两个3的平方，再加7。

生：1+3+5就是3²，后面7+5+3+1是4²，合起来就是25。

师：1+3+5就是黑板上的图几？7+5+3+1是图几？

生：这个式子其实就是黑板上图3和图4的组合。

师：第二题？

生：把这个算式分成两个部分。1+3+5+7+9+11+13=7²，11+9+7+5+3+1=6²，相加是85。

师：这是哪些图形的组合？

生：應该顺下去的第6和第7个图形的组合。

师：想一想9²是什么样子的？

生：就是这样排下去的第9个图形。

生：1+3+5+7+9+11+13+15+17=9²。（学生一边说一边用手指计数）

师：你是怎么想到的？

生：9层就是9个奇数连加！

生：从1开始，9个连续奇数相加的和就是92。

师：观察算式，你发现了什么？

生：加数个数的平方等于加数的和。

师：大家回忆一下，这个规律我们是怎么研究的呀？

师：我们就是借助黑板上这些图形，发现了这些算式的规律。

[赏析]六年级学生认知水平处于从具体运算向逻辑运算的过渡阶段，部分学生不能完全脱离直观来研究逻辑。在第一次练习的环节，教者并没有完全脱离形来研究数，而是在学生说出思考过程后，及时地让学生以形代数、以数表形，解析清楚这样计算的道理，帮助运用规律较慢的学生理解数与形的内在联系。在明确运算规律后，教师解释研究方法，进一步清晰学生对“数形结合”的认识。

[教学片段4]形数结合“慢”拓展

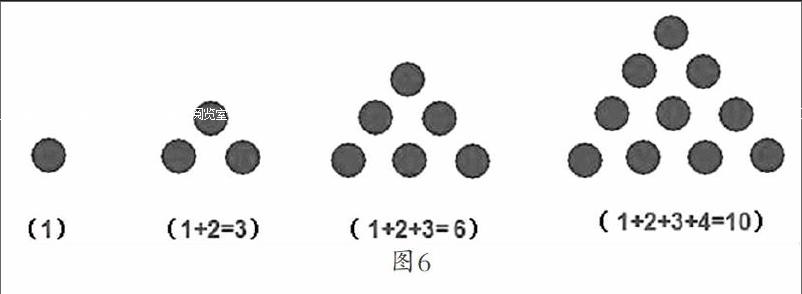
师（逐一出示图6）：这些小圆点拼成了什么图形，有多少个小圆点？

学生一一作答。

师：想象一下，第6个图形是什么样子？

生：有六层，一共是“1+2+3+4+5+6=21”个。

师：1，3，6，10……这些数我们就把它们称为三角形数。

师：那么黑板上这些数，我们就称为……

生：正方形数。

师：为什么叫正方形数？

生：因为排出来都是正方形。

师：想一想，正方形数和三角形数之间有没有什么关系呢？

生：两个三角形数的和。

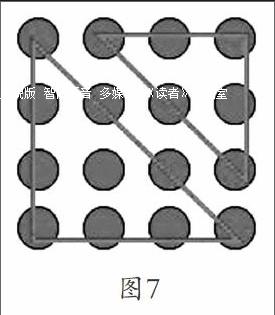
教师出示图7。

师：从刚才的研究中，我们发现.三角形数就是连续自然数的和，正方形数就是连续奇数的和，那么连续偶数的和又是什么样子的呢？大家课后可以去研究一下。

[赏析]彭老师在本环节着力于数与形两个研究对象的相互转化与印证。一边引导学生用数来精确地描述小圆片的总数与排列方式，一边引导学生从排列形式上给“数”命名，如“三角形数”与“正方形数”。随着思考的深入，进一步引导学生思考正方形数与三角形数的联系。学生从直观上很容易发现“一个正方形数就是两个三角形数的和”。教者并未止步，而是以“三角形数就是连续自然数的和，正方形数就是连续奇數的和，那么连续偶数的和又是什么样子的呢？”这个提问为基点，推动学生运用数形结合的方法思考、探究连续偶数之和的规律。