基于匹配度的目标打击武器适宜性分析

杨奇松,王顺宏,王国江,王 宁

(1.火箭军工程大学,陕西 西安 710025;2.解放军61683部队,北京 100094; 3.解放军66136部队,北京 100043)



基于匹配度的目标打击武器适宜性分析

杨奇松1,王顺宏1,王国江2,王 宁3

(1.火箭军工程大学,陕西 西安 710025;2.解放军61683部队,北京 100094; 3.解放军66136部队,北京 100043)

当前弹目适宜性分析中,仅依据弹药毁伤能力进行弹目匹配无法定量描述武器弹药对于特定目标的适宜程度。针对这一问题,对影响武器与目标之间适宜性的因素进行了分析,提出了匹配度的概念;考虑到在武器能够达到预定毁伤要求的情况下,决策者重点关注的是与作战相关的时间因素和价值因素,依据武器所消耗的相对价值和相对时间建立了匹配度的数学模型。结合实例进行了验证实验,实验结果证明该模型准确可靠,对于充分发挥武器弹药效能,进行精确火力筹划具有重要实际应用价值。

弹目匹配;匹配度;火力筹划;毁伤能力

目标打击武器适宜性分析又称弹目匹配,其研究的主要内容为武器对目标的打击可行性与毁伤效能[1]。长期以来,国内外研究的重点始终是“武器-目标分配”问题(Weapon-Target Assignment, WTA)[2],因此,弹目匹配是武器-目标分配问题的基础。本文以导弹武器为研究对象,导弹武器的武器-目标分配问题属于对地打击武器-目标分配问题,其不同于传统的防空拦截武器-目标分配问题,在进行武器-目标分配之前,首先要确定哪些武器可以打,不适合的武器将不再参与后续的武器-目标分配;而且,攻击同一类型的目标往往不会使用多种不同类型的武器,进行弹目适宜性分析可以有效缩减武器-目标分配解的范围[3]。因此只有将两者结合起来,才是完整的火力运用。

目前WTA问题的模型与算法研究已经取得了较多的成果[2],而弹目适宜性的研究长期处于一种定性研究的层面,这可以在一定程度上解决给定打击目标清单的情况下,哪些武器弹药可以打的问题,却不能清晰地描述特定武器针对特定目标的适宜程度,以至于无法确定武器弹药使用的优先顺序。本文针对这一问题,提出弹目匹配适宜度的概念,并建立了匹配度的数学模型,结合具体实例进行了仿真验证,目的在于以一种定量的指标去衡量目标打击武器的适宜程度。这对于优化配置火力资源,最大可能的发挥武器弹药的效能,降低作战风险,在信息化条件下达成决策制胜(快速、精准决策)的要求意义重大。

1 弹目适宜性的匹配度模型

从决策者的意图层面上讲,在能够达到预期作战目的的情况下,决策者关注的重点在于作战所花费的时间和消耗的价值,而武器本身的能力与这两者关系密切。因此,建立匹配度模型目的在于以作战花费时间和消耗价值客观反映出武器的能力,并能够在一定程度上体现决策者的决策思维。

1.1 射击可能性检查

在判断武器是否适合打击特定目标时,首先要满足一些基本条件[7];若不满足,则该类武器将不予考虑,本文将射击可能性检查分为:

1)射程适宜性PS,假如导弹武器的作战范围范围能够覆盖目标,则PS=1;否则,PS=0;

2)末制导适宜度PZ,如果作战环境不满足制导条件约束,那么PZ=0;否则,PZ=1;

3)附带损伤适宜性PF,如果武器对敏感设施造成附带损伤的可能性达到了一定程度,那么PF=0;否则,PF=1。

(1)

本文引入“匹配条件”的概念,即武器与目标匹配所必须满足的条件,即

(2)

若当前作战环境下,导弹武器不能满足匹配条件,则匹配度PP直接取最小值0,即可判定武器与目标不匹配;若满足“匹配条件”,则可进行后续匹配度计算,只要PP取大于0的某个值,则证明武器对于目标有一定程度的适宜性。

1.2 武器价值消耗

在武器弹药的火力控制范围可以有效覆盖目标,且末制导条件适宜的情况下,达到预定毁伤要求的弹药消耗价值可以充分体现出武器弹药的毁伤能力。在已知武器的CEP和对目标毁伤半径的情况下,弹药消耗价值可以通过模拟试验的方法进行仿真计算得到,本文主要采用像素仿真法进行计算[10]。文献[11-12]给出了导弹突防概率PT的简化计算方法,本文不再阐述。

达到预定毁伤要求消耗的弹药实际价值是在基于成功突防的假设条件下得到的,但实际作战中必然会有导弹未能成功突防而被拦截。因此,必须保证足够数量的导弹突防,才能使最终的毁伤达到预期效果,每类弹药的实际消耗价值为

(3)

其中,Ni,Vi和Vi′分别代表第i类武器弹药达到预定毁伤要求所消耗的弹药数量和考虑突防概率前后消耗的实际价值;vi为第i类武器弹药的实际单位价值。

实际进行弹目匹配的过程中,武器弹药的种类往往是一定的,问题的关键在于对其进行比较。考虑到在最终匹配度的建模中,由于概率与价值的量纲存在较大差距,会使弹目匹配结果产生较大偏差,与作战实际相悖。因此需要对武器的价值进行归一化处理,引入相对价值PV∈(0,1],基本过程如图1所示。

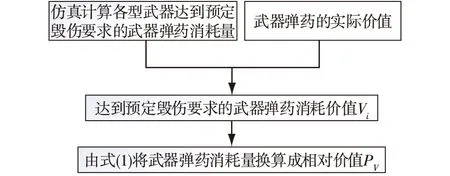
图1 相对价值计算

假设有n类待选武器弹药,其达到预定毁伤要求所消耗的价值分别为V1,V2,…,Vn。其中第k类消耗的实际价值最高,则其相对价值PVk=1,那么第i类武器弹药的相对价值为PVi:

(4)

1.3 作战时间消耗

在信息化条件下,战争节奏明显加快,战争有利时机稍纵即逝。尤其对于时间敏感目标,其往往是具有重要价值的目标,或者对己方构成严重威胁的目标,对于此类目标,需要己方迅速做出反应,以最快速度将其消灭。因此要优先选择完成整个作战过程(发现、识别到打击完成)时间最短的武器弹药,以武器所消耗的相对时间PH进行评价。

n类待选武器弹药完成整个作战过程所消耗的时间分别为T1,T2,…,Tn。其中第k类消耗的时间最长,则其消耗的相对时间PHk=1,那么第i类武器消耗的相对价值为PHi:

(5)

1.4 匹配度模型

在作战实际中,由于决策者意图的存在以及实际战场需求等方面的原因,可能导致在进行弹目匹配的过程中,对各时间因素和价值因素的关注程度有所不同,这也是在构建匹配度模型的过程中需要重点关注的因素。因此,匹配度PP绝不是几个匹配指标简单相加或者连乘得到。为了体现这种区别,特引入价值权重KV和时间权重KT,满足KV+KT=1。整个匹配度计算流程如图2所示。

图2 匹配度计算流程

那么,匹配度PP便可由下式计算得到:

(6)

2 确定指标权重

层次分析法(AnalyticHierarchyProcess,AHP)是适用范围很广的定性定量相结合的多准则决策评价方法,把复杂问题分解成各个组成因素,又将这些因素按支配分组形成递阶层次结构,通过两两对比的方式确定同一层次中诸因素的相对重要性,然后综合决策者的判断,确定备选方案相对重要性的总排序,整个过程体现了人的决策思维的基本特征,即分解、判断和综合。在匹配度模型中,虽然第二层指标数量仅有价值和时间,但各自的侧重点十分明确,适合用层次分析法确定两者的权重[14]。

2.1 构造判断矩阵

将时间因素与价值因素的重要程度进行比较,得到判断矩阵。通常采用Saaty标度法进行相对重要程度赋值,不仅直观,并且保证了精度。aij表示指标Pi相对于指标Pj“重要程度”的判断值,具体取值按表1选取。

表1 因素比较重要程度判断值表

令判断矩阵A为

(7)

根据指标之间的相互关系及矩阵的相关特性,显然有如下关系式:

(8)

在作战决策的背景下,一般由决策者给出判断矩阵,当有n名决策者共同该出判断矩阵时,采用几何平均法计算判断矩阵元素,即

(9)

2.2 权重计算

指标权重计算就是计算判断矩阵A最大特征根λmax对应的特征向量Y,该向量经归一化后的分量即为相应指标的权重。求解AY=λmaxY的方法有和积法、方根法、幂法等。本文采用Satty给出的近似计算方法,其误差在允许的范围之内,算法如下:

A中每行元素连乘后开方，有

(10)

求各指标的权重：

(11)

将A中每列元素求和：

(12)

计算最大特征值：

λmax=wVSV+wHSH

(13)

在得到各指标权重之后,需要进行一致性检验以消除判断思维和主观认识的不一致性,具体过程参考文献[14],本文不再赘述。

3 模拟实验与结果比较

3.1 实验设计

假定我方地地弹道导弹部队要携带表2所示四种武器中的一种执行对某国X空军基地的计划打击任务,以实现对其主跑道的有效封锁,为夺取制空权,掌握战争主动性创造条件。

跑道信息如表3所示,其中毁伤要求的定义为,跑道上不存在飞机最小起降窗口的概率(跑道失效率)达到规定数值。

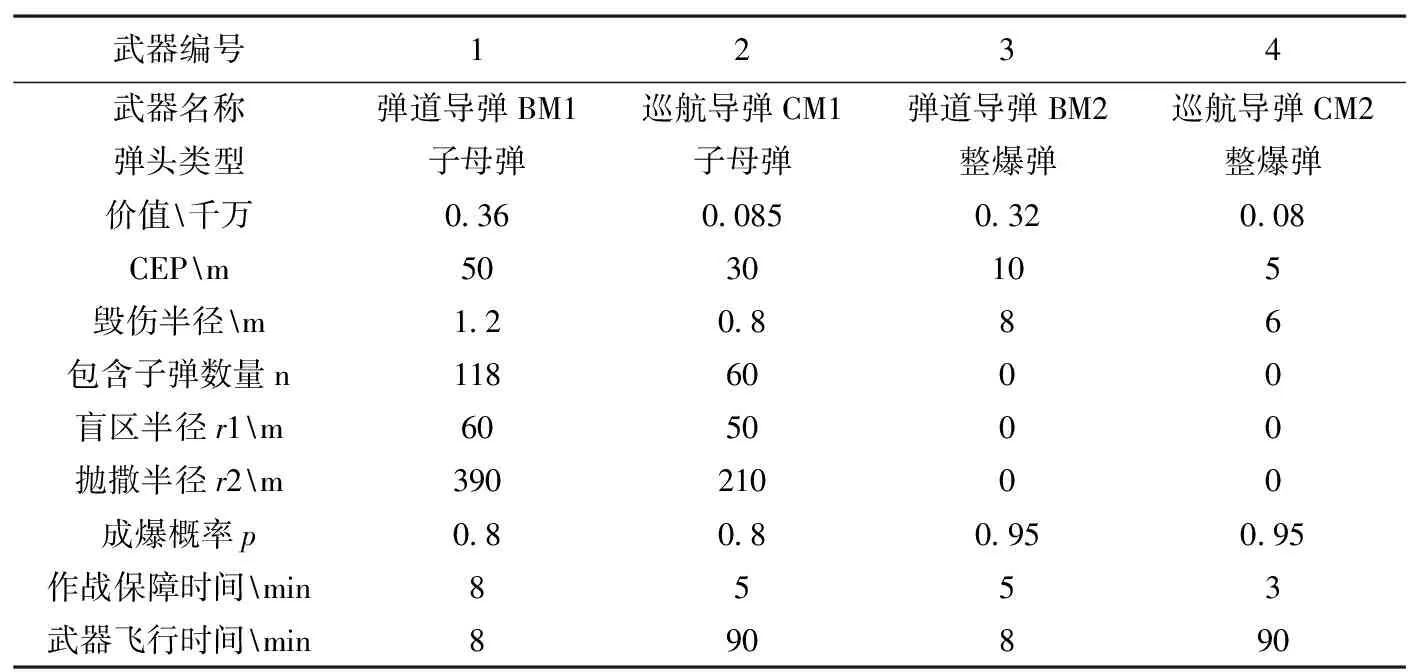
表2 武器信息

假设空军基地附近驻有防空导弹阵地Y,该导弹阵地装备了C型地空导弹,可有效实施对巡航导弹和弹道导弹的拦截。其相关参数如表4所示,其中毁伤半径指的是C型地空导弹对导弹类武器的毁伤半径,这里不作导弹武器类型的区分。

巡航导弹CM1和CM2经过航迹规划后可有效避开的拦截区;而弹道导弹武器平台虽然可以选择在敌防区外进行投射,但飞行轨迹无法绕开防空导弹阵地的拦截区,敌防空导弹阵地Y对弹道导弹采取“二拦一”的策略。

3.2 相关参数解算

依据表2和表3中的信息,使用像素仿真法计算出各型武器达到预定毁伤要求所消耗的弹药数量及价值,如表5所示。采用文献[11]中方法对弹道导弹BM1和BM2突防防空导弹阵地Y的突防概率进行估算,如表5所示。

表5 计算结果

将表2和表5中的数据代入式(4)和式(5)中,便可以得到各型武器消耗的相对时间和相对价值,如表5所示。

表6 消耗相对时间和相对价值计算结果

3.3 仿真结果与分析

随着价值因素相对于时间因素“重要程度”判断值aVH的变化,价值权重与时间权重的取值如表7所示。

表7 价值权重与时间权重的取值

算例中的四类武器均满足上文所述的最基本条件,因此,它们对于X基地的跑道目标均有一定程度的适宜性。将表6和表7中的数据代入公式(6)可以得到各型武器在不同判断值aVH下的匹配度,如表8和图 3所示。

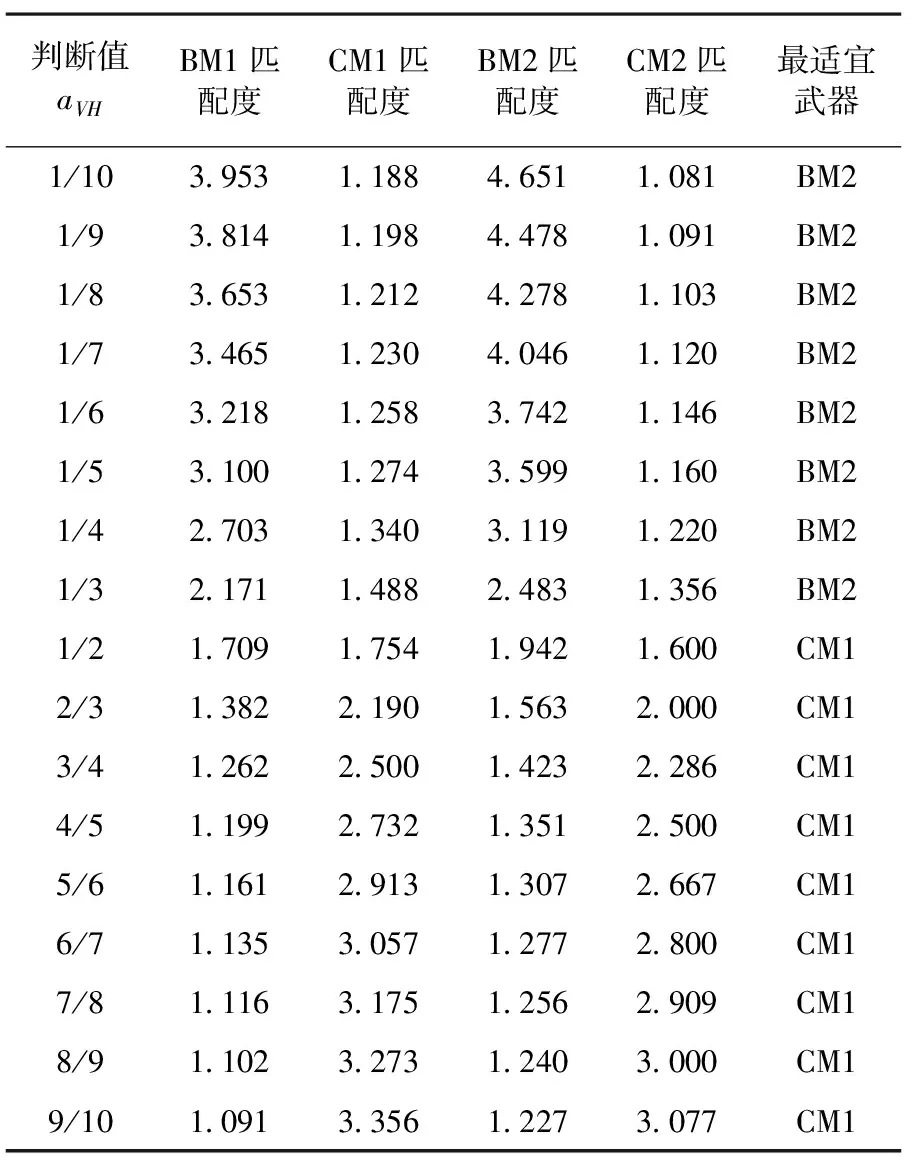
表8 匹配度计算结果

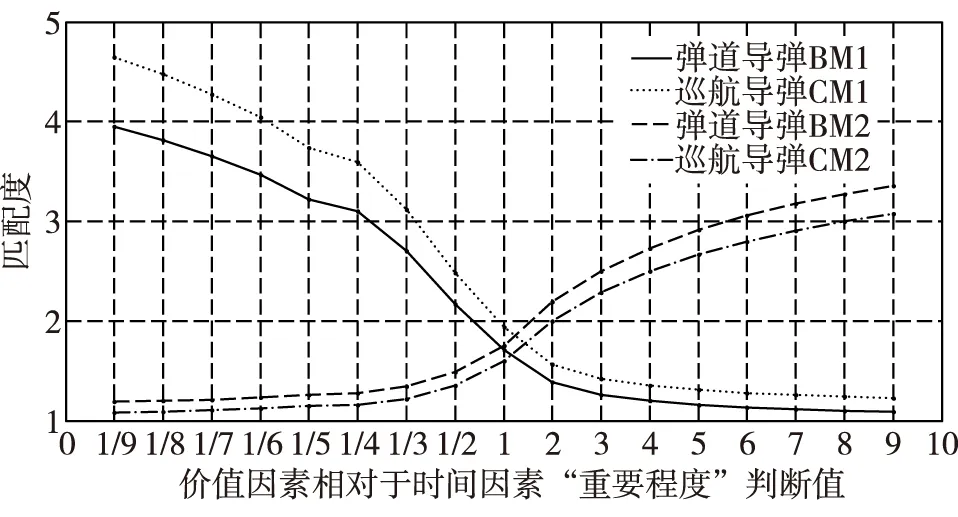
图3 匹配度计算结果

由上述计算结果可以得出以下结论:

1)当决策者对于价值因素和时间因素关注程度相当时,由于弹道导弹所耗费飞行时间较于巡航导弹优势明显,弹道导弹的匹配度计算结果要明显优于巡航导弹,此时弹道导弹BM2与目标之间的适宜程度最高。

2)当决策者认为价值因素更为重要时,巡航导弹类武器价值较低的优势(通常对于同射程的巡航导弹和弹道导弹,弹道导弹的造价是巡航导弹的4-6倍)使得CM1和CM2的匹配度要高于BM1和BM2,且随着这种关注程度的增加,BM1、BM2同CM1、CM2之间匹配度的差异越来越大,此时巡航导弹CM1与目标之间的适宜程度最高。

3)当决策者认为时间因素更为重要时,弹道导弹类武器飞行马赫数较高的优势使得BM1和BM2的匹配度要高于CM1和CM2,且随着这种关注程度的增加,BM1、BM2同CM1、CM2之间匹配度的差异越来越大,此时弹道导弹BM2与巡航导弹之间的适宜程度最高。

4 结束语

本文建立了匹配度模型,给出了详细的计算步骤。在评价武器能力方面,匹配度以量化武器目标之间的适宜程度为出发点,将武器的射程、突防能力、毁伤能力、制导因素等进行了综合,最终反映在作战花费的时间和消耗的价值上;从决策意图层面上讲,在能够达到预期作战目的的情况下,决策者关注的重点在于作战所花费的时间和消耗的价值,因此以权重系数来表征对时间和价值因素的侧重程度在一定程度上体现了决策者的决策思维。匹配度将武器能力与作战意图相结合,更加贴近战场实际。从仿真结果来看,整个计算过程简单,武器能力的优劣和决策意图的偏倚都在匹配度具体数值上得到了体现,达到了预期效果,匹配度模型为量化武器目标之间的适宜程度提供了一种有效的方法。

[1] 任富兴,王雪琴.联合火力战毁伤理论[M].北京:解放军出版社,2010.

[2] 蔡怀平,陈英武.武器-目标分配(WTA)问题研究进展[J].火力与指挥控制,2006,32(12):11-15.

[3] 李勇君,黄卓,郭波.武器-目标分配问题综述[J].兵工自动化,2009,28(11):1-4.

[4] Morris R. Driels. Weaponeering:Conventional Weapon System Effectiveness[M]. American Institute of Aeronautics and Astronautics,2004.

[5] Patrick A, Hosein M A. Preferential Defense Strategise[R]. LIDS-P-2002, 1990.

[6] Patrick A, Hosein M A. Some Analytical Results for the Dynamic Weapon-Target Allocation Problem[R]. LIDS-P-1944,1990.

[7] 卢芳云,蒋邦海,等.武器战斗部投射与毁伤[M].北京:科学出版社,2013.

[8] 李向东,杜忠华. 目标易损性[M]. 北京:北京理工大学出版社,2013.

[9] J.Terrence Kolpcic, Harry L. Reed. Historical Perspectives on Vulnerability/Lethality Analysis. US Army Research Laboratory, Apr, 1999, AD-A361861.

[10]陈立新.像素——仿真法研究[J].指挥技术学院学报,1999,10(6):80-83.

[11]马成栋.弹道式导弹突防概率的估算[J].北京航空航天大学学报,1991(4):30-40.

[12]谢邦荣.巡航导弹对地空导弹的突防概率仿真研究[J].系统仿真学报,2004,16(12):2687-2695.

[13]李勇.末修子母弹对机场跑道封锁概率计算仿真研究[J].系统仿真学报,2006,18(9):2397-2400.

[14]岳超源.决策理论与方法[M].北京:科学出版社,2001.

[15]杨世荣.多跑道机场最优瞄准点选择方法研究[J].火力与指挥控制,2000,25(2):53-55.

[16]United States Joint Forces Command/J9 Director, Engineering Experimentation Division.JWARS Joint Analyst Guide[M].The Joint Warfare System Program Office.2006.

[17]Cullenbine C. A Tabu Search Approach to the Weapon Assignment Model[R].AFIT/GOR/ENS/00M-08, 2000.

[18]Silven S. A Neural Approach to the Assignment Algorithm for Multiple-Target Tracking[J]. IEEE Journal of Oceanic Engineering. 1992, 17(4): 1-7.

[19]Lee Zne-Jung, Su Shun-Feng, Chou-Yuan Lee.Efficiently Solving General Weapon-Target Assignment Problem by Genetic Algorithms with Greed Eugenics[J].IEEE Journal on Systems,Man, And Cybernetics-Bart B Cybernetics. 2003, 33(1):119-120.

Weapon-Target Matching Analysis Based on Matching Degree

YANG Qi-song1, WANG Shun-hong1, WANG Guo-jiang2, WANG Ning3

(1. Rocket Force Engineering University, Xi’an 710025; 2. the Unit 61683 of PLA, Beijing 100094; 3. the Unit 66136 of PLA, Beijing 100043, China)

In the present weapon-target matching research, the matching standard is only the damage capacity of the warhead and weapons’ suitability for the target cannot be quantitatively described. To solve this problem, the analysis of the factors influencing weapon-target matching is carried out, and the concept of matching degree is put forward. In the case of the weapon to fulfil its mandate, the decision maker focused on the time factor and value factor, so the mathematical model is built based on the counter consuming time and value of the weapon. The results of simulated experiment indicate that this model is reliable. It’s meaningful to make full use of weapon efficiency and carry out accurate fire allocation.

weapon-target matching; matching degree; fire allocation; damage capacity

2016-06-05

2016-07-13

杨奇松(1993-),男,湖北襄阳人,硕士研究生,研究方向为飞行动力学与制导。 王顺宏(1975-),男,副教授,硕士生导师。 王国江(1974-),男,工程师。 王 宁(1982-),男,硕士。

1673-3819(2017)02-0061-06

E917

A

10.3969/j.issn.1673-3819.2017.02.013