基于折线简化的方位导引方法的可用性研究
2017-05-11徐继华袁富宇
徐继华,袁富宇
(江苏自动化研究所,江苏 连云港 222000)
基于折线简化的方位导引方法的可用性研究
徐继华,袁富宇
(江苏自动化研究所,江苏 连云港 222000)
针对方位导引过程的导引参数计算(折线转弯参数计算、曲线转弯参数计算)、导引过程模拟(折线转弯模拟、曲线转弯模拟)分别进行仿真计算,考察发现概率的差别并对比分析。仿真结果表明,主动声自导和被动声自导鱼雷可以使用折线转弯来简化导引参数计算和导引过程模拟,尾流自导鱼雷只能使用折线转弯来简化导引参数计算而不能使用折线转弯进行发现概率的计算。
方位导引;折线转弯;曲线转弯;发现概率
方位导引法是潜载鱼雷线导攻击的主要导引方法,其导引准则是将鱼雷引导到上一时刻、现在时刻或下一时刻的导引平台和目标连线上,即目标方位线[1]。
现有的方位导引法是将鱼雷曲线转弯运动简化为折线过程进行计算的,但是实际上鱼雷在每个导引周期的运动都是由先曲线转弯再直线航行组成的。另外现有线导鱼雷发现目标或尾流的仿真方法也是将鱼雷导引运动简化为折线过程后进行模拟的。那么,这样的简化是否合理有效呢?在公开出版或发表的著作和文章中都没有见到有关的论证或仿真说明。这关系到对方位导引效果的“解析”评估:如果简化(折线转弯)是可行的,将给导引效果评估[2]的“解析”评估带来方便,否则,会使得评估模型很复杂。
本文将针对方位导引过程的导引参数计算(折线转弯参数计算、曲线转弯参数计算)、导引过程模拟[3](折线转弯模拟、曲线转弯模拟)分别进行仿真计算对比分析,考察两者发现概率的差别。
1 现有方位导引法简介[4]
1.1 带符号距离
普通意义下的距离是不小于零的,在本文中为应用方便,定义一种有符号的距离,称为带符号距离。
同样,直线是无方向的,因此,也给直线定义一个方向。这是为定义带符号距离做准备。设直线方程为
Ax+By+C=0
(1)

不难证明,当直线方程由式(1)给出时,P(x0,y0)到直线(1)的带符号距离D可写为
(2)
1.2 方位导引模型
方位导引就是把鱼雷导引到某时刻导引平台量测到的目标方位线上,如图1所示,在时刻i,鱼雷位于ti点,导引平台位于Oi点,方位线为Bi,此时要计算出鱼雷下一时刻导引航向Ct1。
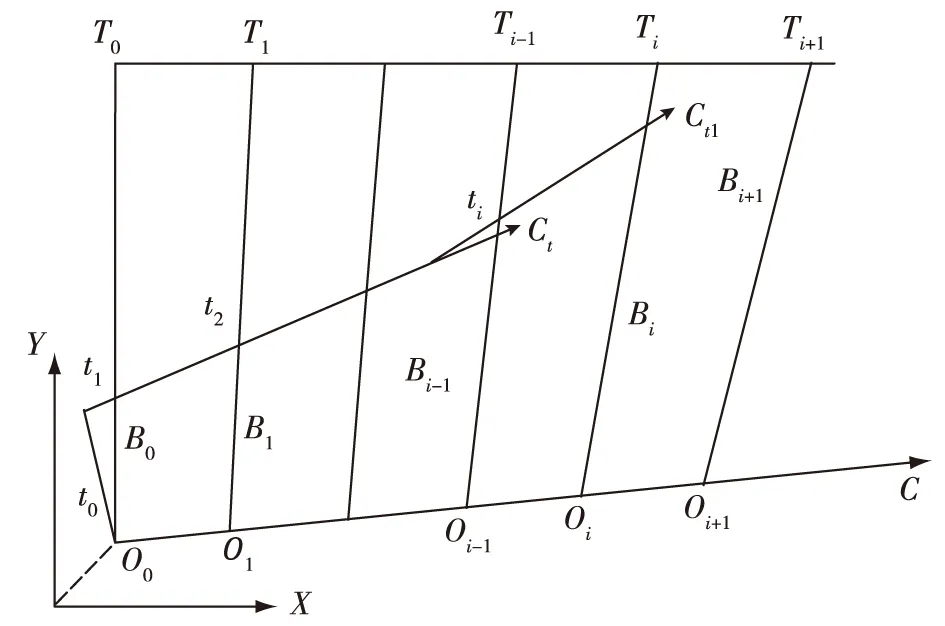
图1 折线转弯导引过程态势示意图
由图1知,求Ct1的已知条件为鱼雷位置ti(xt,yt),导引平台位置Oi(xo,yo)及目标方位Bi。假设等间隔采样,每一采样间隔鱼雷航程为St,鱼雷导引点与雷头距离为Rc,Ct1与Bi线的夹角为α,ti到方位线Bi的带符号距离为Di。
易得Bi方位线的方程为
cosBi·(x-xo)-sinBi·(y-yo)=0
(3)

图2 折线转弯导引过程的导引参数计算示意图
鱼雷到方位线Bi关于方程(4)的带符号距离为Di,由前面讨论知,从导引平台位置观察,当鱼雷位于方位线Bi左侧时Di>0,位于右侧时Di<0。
由正弦定理可得
(4)
α与Di同号。进而得到
Ct1=Bi+α
(5)
ω=Ct1-Ct
(6)
2 精确导引参数计算方法
上文描述的是鱼雷折线转弯的导引参数计算模型,本节根据鱼雷实际导引过程来推导严格的导引参数计算模型,其中鱼雷以曲线运动完成转弯(或转角),曲线用圆弧来逼近,称为“精确导引参数计算”。本文在大地直角坐标系下推导计算模型。
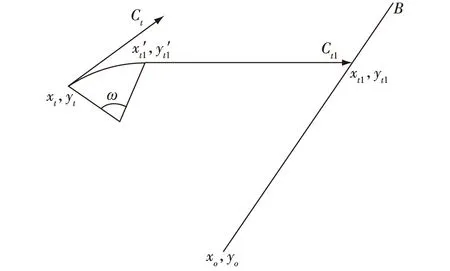
图3 曲线转弯导引过程的导引参数计算示意图

求得目标方位线方程为
(y-yo)·sinB-(x-xo)·cosB=0
(7)
导引结束后鱼雷自导扇面形心应位于目标方位线上,将(xt1,yt1)为表达式代入(8),并整理得到关于导引转角的非线性方程:
(Vt·Δt-Rt·|ω|+Rc)·sin(Ct+ω-B)+

(xt-xo)·cosB-(yt-yo)·sinB=0
(8)
3 精确导引目标发现判断方法
精确导引发现判断就是考虑鱼雷弧线转弯的情况下去计算鱼雷坐标位置和判断鱼雷是否发现目标,折线转弯导引发现判断就是考虑鱼雷瞬间完成转弯的情况下去计算鱼雷坐标位置和判断鱼雷是否发现目标,亦即仅考虑鱼雷在直航段是否发现目标。
3.1 精确被动声自导鱼雷发现目标判断方法
1) 精确被动声自导鱼雷转弯发现目标判断方法

逐步判定,i=1,2…n:

目标相对雷头的方位:
(9)
鱼雷自导扇面左右边缘线方向分别为Ctl=Cti-α和Ctr=Cti+α;
雷目距离
(10)
判断目标是否位于鱼雷自导扇面夹角内:
若(BTi-Ctl)(BTi-Ctr)<0,并且di 其中,Rmax为鱼雷声自导扇面半径,(xTi,yTi)、(xti,yti)为相应时刻目标和鱼雷位置坐标。 2) 精确被动声自导鱼直航发现目标判断方法 目标相对运动方程: rxT(t)=xT+rVTx·t (11) 其中Ct为鱼雷转角后的直航航向。 通过判断目标相对运动轨迹与上述鱼雷自导扇面各边缘线是否有交点,即可判断是否发现目标。 3.2 精确主动声自导鱼雷发现目标判断方法 主动声自导鱼雷发现目标的判断方法与被动声自导鱼雷基本相似,唯一的不同在于被动声自导的命中点在螺旋桨(点目标),而主动声自导的命中点在目标舰身(线目标)。对于线目标来说,只要有其上任意一点进入鱼雷发现范围,则标记发现目标,具体做法不再赘述。 3.3 精确尾流自导鱼雷发现目标判断方法 1) 精确尾流自导鱼雷转弯发现目标判断方法 设有效尾流近点坐标为(xw1,yw1),有效尾流远点坐标为(xw2,yw2)。 若(xc-xw1)·(xc-xw2)<0或者(yc-yw1)·(yc-yw2)<0,并且入尾流角满足设定条件,则标记发现目标尾流。 2) 精确尾流自导直航发现目标判断方法 假定目标不动,鱼雷做相对运动,计算有效尾流近点远点坐标分别为(xw1,yw1)和(xw2,yw2),鱼雷雷头到有效尾流两端点的方位为Cw1,Cw2。 鱼雷相对航向为 (12) 若(rCt-Cw1)·(rCt-Cw2)<0,并且鱼雷能够穿越目标航线,则标记发现目标。 4.1 仿真态势 目标初距设定为5km、10km、15km、20km、25km、30km,目标速度设定为10kn、20kn、30kn,目标初始舷角设定为30°、60°、90°、120°、150°,导引平台初始舷角分别为0°、±30°、±60°、±90°,共630个不同态势,设定鱼雷航程为50km。 鱼雷速度设定为40kn,主/被动自导扇面半径设定为1000m,自导扇面半角设定为42°。 目标长度设定为130m,目标尾流有效长度设定为3min×目标航速(m/s),无效长度设定为60m。 4.2 仿真次数 每个态势模拟10000次,统计每个态势下的发现概率。 4.3 叠加误差 目标方位量测误差:σB=0.5°。 平台导航误差:平台航向误差σCO=0.2°;平台速度误差σVO=0.15kn。 鱼雷速度、转角、偏航、导航误差:速度误差σVt=2kn;转角误差σω=1°;偏航误差σCt=2.5%(弧度);导航误差σVtn=0.1kn,σCtn=0.1°。 4.4 计算结果 各种组合情况下得到的发现概率如图4-图6所示,横坐标为不同的态势,初始态势为导引平台舷角-90°,目标初距5km,目标速度10kn,目标舷角30°,态势由目标舷角(最内层循环)开始递增组合变化。纵坐标为发现概率之差。 4.4.1 方位导引+被动声自导(图4) 图4 被动声自导鱼雷仿真对比结果 1)“折线转弯参数计算+折线转弯发现判断”与“曲线转弯参数计算+折线转弯发现判断” 比较结果: 误差大于10%的态势0个;误差在5%到10%的态势1个,占总态势的0.16%;误差小于5%的态势629个,占总态势的99.8%。 2)“折线转弯参数计算+曲线转弯发现判断”与“曲线转弯参数计算+曲线转弯发现判断”的比较结果: 误差大于10%的态势有0个;误差在5%到10%的态势有2个,占总态势的0.32%;误差在5%以下的态势有628个,占总态势的99.7%。 3)“折线转弯参数计算+折线转弯发现判断”与“折线转弯参数计算+曲线转弯发现判断”的比较结果: 误差大于10%的态势有7个,占总态势的1.1%,误差在5%到10%的态势有47个,占总态势的7.5%;误差在5%以下的态势有576个,占总态势的91.4%。 4)“曲线转弯参数计算+折线转弯发现判断”与“曲线转弯参数计算+曲线转弯发现判断”的比较结果: 误差大于10%的态势有1个占总态势的0.16%,具体态势为本艇舷角-30°,目标初距10km,目标速度30kn,目标舷角150°,发现概率之差为14.26%;误差在5%到10%的态势有53个,占总态势的8.4%;误差在5%以下的态势有576个,占总态势的91.4%。 4.4.2 方位导引+主动声自导(图5) 1)“折线转弯参数计算+折线转弯发现判断”与“曲线转弯参数计算+折线转弯发现判断”的比较结果: 误差大于10%的态势有0个;误差在5%到10%的态势有4个,占总态势的0.48%;误差在5%以下的态势有627个,占总态势的99.5%。 2)“折线转弯参数计算+曲线转弯发现判断”与“曲线转弯参数计算+曲线转弯发现判断”的比较结果: 误差大于10%的态势有0个;误差在5%到10%的态势有4个,占总态势的0.64%;误差在5%以下的态势有626个,占总态势的99.4%。 3)“折线转弯参数计算+折线转弯发现判断”与“折线转弯参数计算+曲线转弯发现判断”的比较结果: 误差大于10%的态势有80个,占总态势的12.7%;误差在5%到10%的态势有57个,占总态势的9%;误差在5%以下的态势有493个,占总态势的78.3%。 4)“曲线转弯参数计算+折线转弯发现判断”与“曲线转弯参数计算+曲线转弯发现判断”的比较结果: 误差大于10%的态势有91个,占总态势的14%;误差在5%到10%的态势有53个,占总态势的8.4%;误差在5%以下的态势有486个,占总态势的77.1%。 4.4.3 方位导引+尾流自导(图6) 图6 尾流自导鱼雷仿真对比结果 1)“折线转弯参数计算+折线转弯发现判断”与“曲线转弯参数计算+折线转弯发现判断”的比较结果: 误差大于10%的态势有0个;误差在5%到10%的态势有8个,占总态势的1.3%;误差在5%以下的态势有622个,占总态势的98.7%。 2)“折线转弯参数计算+曲线转弯发现判断”与“曲线转弯参数计算+曲线转弯发现判断”的比较结果: 误差大于10%的态势有0个;误差在5%到10%的态势有6个,占总态势的0.95%;误差在5%以下的态势有624个,占总态势的99%。 3)“折线转弯参数计算+折线转弯发现判断”与“折线转弯参数计算+曲线转弯发现判断”的比较结果: 误差在10%以上的态势有336个,占总态势的53.3%;误差在5%到10%的态势有103个,占总态势的16.3%;误差在5%以下的态势有191个,占总态势的30.3%。 4)“曲线转弯参数计算+折线转弯发现判断”与“曲线转弯参数计算+曲线转弯发现判断”的比较结果: 误差在10%以上的态势有331个,占总态势52.5%;误差在5%到10%的态势有109个,占总态势的17.3%;误差在5%以下的态势有190个,占总态势的30.2%。 4.5 结果分析 通过以上结果对比可以看出,对于被动声自导鱼雷来说,在折线与曲线参数计算方法的对比中,无论是使用折线还是曲线转弯发现判断都没有大于10%的误差,这表明使用折线转弯来简化导引参数计算是可以的。在折线转弯发现判断和曲线转弯发现判断的对比中出现了一些误差大于10%的态势,可以看出大于10%的误差主要的影响因素是目标舷角。误差在10%以上的态势基本上都是目标舷角为120°和150°。误差在5%到10%的态势最高占总态势的8.4%,这是完全可以接受的。 对于主动声自导鱼雷,在折线与曲线参数计算方法的对比中没有大于10%的误差,因此主动声自导鱼雷也是可以使用折线转弯来简化导引参数计算。在折线转弯发现判断和曲线转弯发现判断的对比中,误差大于10%的态势稍多,通过统计误差分布(数据较多,由于本文篇幅所限就不再罗列),发现影响这些误差的因素主要为目标舷角,次要为目标速度,与目标初距和本艇舷角的关系不大,因此在避开目标舷角和目标速度较大的态势(通常在实战中也不会选择这些态势来发射鱼雷)的情况下,用折线过程来简化模拟导引过程也是没有问题的。 对于尾流自导鱼雷来说,通过折线和曲线参数计算方法对比的结果可以看出,尾流自导鱼雷同主被动声自导鱼雷一样可以使用折线参数计算方法来简化参数计算过程。但是无论是使用折线参数计算方法还是曲线参数计算方法,其折线与曲线转弯发现判断的发现概率差别都很大,折线参数计算情况下,误差10%以上的态势有336个,占总态势的53.3%,曲线参数计算情况下,误差10%以上的态势有331个,占总态势52.5%。这是因为尾流自导鱼雷不像被动声自导和主动声自导鱼雷有自导扇面,它必须要穿越目标有效尾流上某一点才能发现目标,这样鱼雷是曲线转弯还是折线转弯对发现概率的影响就会变得很大(因为折线转弯相当于鱼雷没有转弯过程),因此,不能使用折线过程来简化模拟尾流自导鱼雷的转弯运动。 本文通过大量的仿真实验验证了被动声自导鱼雷和主动声自导鱼雷(大部分态势)可以使用折线转弯来简化导引参数计算和导引过程模拟,尾流自导鱼雷可以使用折线转弯来简化导引参数计算,但是不能使用折线转弯来简化导引过程模拟。 下一步的工作将考虑鱼雷折线过程的“解析”评估模型,这种模型在保证一定精准度的前提下会大大加快得到鱼雷发现概率的速度。本文的研究结果也为“解析”模型的进一步研究打下了基础。 [1] 赵正业.潜艇火控原理[M].北京:国防工业出版社,2003. [2] 孟庆玉,张静远,宋保维.鱼雷作战效能分析[M].北京:国防工业出版社,2003. [3] 张静远.鱼雷作战使用与作战能力分析[M].北京:国防工业出版社,2005. [4] 袁富宇.现在方位导引方法的一种变形[A].1993年数学建模与软件学术会议论文集[C].连云港,1993:402-405. [5] 张旭.线导鱼雷使用中若干问题的探讨[J].鱼雷技术,2001,9(2):42-44. Research on Usability of Directional Guidance MethodBased on Simplification of Polyline XU ji-hua, YUAN Fu-yu (Jiangsu Automation Research Institute, Lianyungang 222061, China) The calculation of guiding parameters (calculation of curve turning parameters, calculation of curve turning parameters), guidance process simulation (turning curve simulation, curve turning simulation) of the azimuthal guidance process are carried out respectively, and the difference of probabilities is found and compared. Simulation results show that active acoustic homing and passive acoustic homing torpedoes can simplify the calculation of guiding parameters and guide process simulation by using polyline turning. The trajectory homing torpedo can only use the polyline turning to simplify the calculation of guiding parameters and can not use the polyline Turning to calculate the probability of discovery. directional steering; polyline turning; curved turning; probability of discovery 2016-12-02 2017-01-09 徐继华(1990-),男,山东济宁人,硕士研究生,研究方向为鱼雷武器。 袁富宇(1964-),男,博士,研究员。 1673-3819(2017)02-0031-05 TJ630;E917 A 10.3969/j.issn.1673-3819.2017.02.007
ryT(t)=yT+rVTy·t
rVTx=VT·sinCT-Vt·sinCt
rVTy=VT·cosCT-Vt·cosCt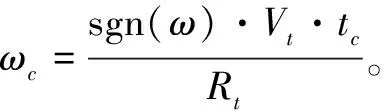
4 仿真实验
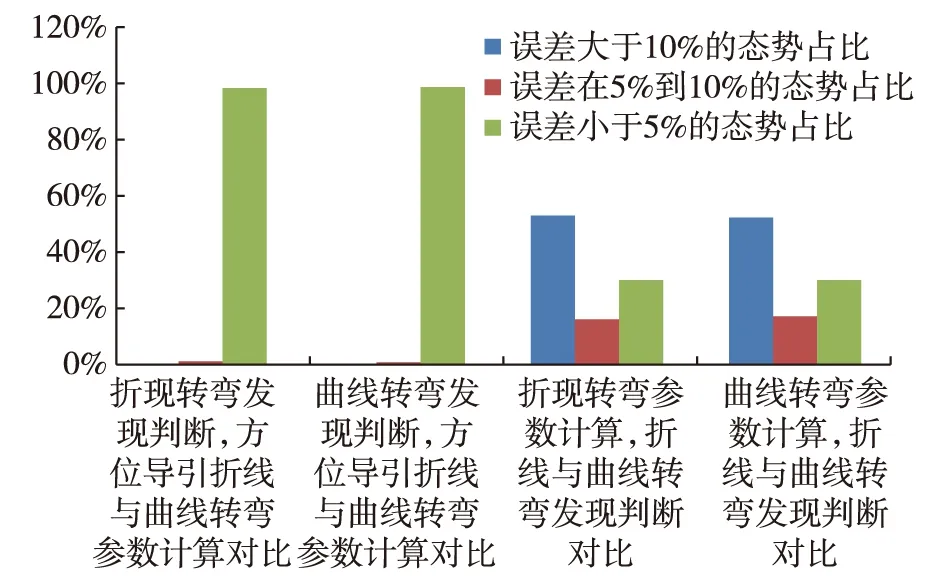
5 结束语
