SVR和BP在对空威胁评估中的应用*

王 芳,张军辉,吴志泉

(1.海军大连舰艇学院,辽宁 大连 116018;2. 91982部队,海南 三亚 572000)



SVR和BP在对空威胁评估中的应用*

王 芳1,张军辉2,吴志泉1

(1.海军大连舰艇学院,辽宁 大连 116018;2. 91982部队,海南 三亚 572000)

为提高对空中目标威胁值评估的灵活性和适应性,首先设计了基于回归型支持向量机和BP神经网络的空中目标威胁值评估流程图;选择了空中目标的威胁因素,确定了数据归一化的处理标准;细化了SVR模型和BP模型的训练步骤。通过实例分别对两个模型进行了应用,并使用Matlab软件验证了威胁值评估结果的正确性和准确性;最后对SVR模型和BP模型的优缺点进行了分析和比较,得出SVR模型更适用于当前对空威胁评估的结论。

支持向量机;神经网络;空中目标;威胁评估

随着科学技术的迅猛发展,未来的海战中,水面舰艇对空防御将面临战场环境复杂多变、敌我态势变化迅速、战机稍纵即逝的形势。如何对空中目标的威胁值进行合理、准确地评估,为指挥员合理分配火力提供重要依据,是一个需要深入研究的关键问题。目前威胁值的评估模型很多,有层次分析法、专家系统法、灰色聚类法、贝叶斯网络法、模糊理论法[1],这些模型的威胁判断规则是固定不变的,即事前确定好模型所需的输入变量个数与类型、模型威胁值的计算公式等;同时模型也是在特定的作战背景下建立的,这一定程度上影响了威胁值评估的准确性,特别是当战场环境发生变化时,威胁判断结果的可靠性无法保证。随着计算机技术的不断发展和各种智能算法的推陈出新,威胁判断必然向信息化和智能化方向发展。本文根据未来水面舰艇单舰对空防御的作战特点,分别应用回归型支持向量机和误差逆向传播神经网络的算法解决威胁值评估的问题,以提高空中目标威胁判断结果的准确性和可靠性。

1 基本理论

对空威胁判断中,目标威胁值的确定本质上是对威胁值进行非线性分类。分类是通过某个分类函数把输入数据映射到给定类别中的某一个,达到预测未知数据类别的目的,支持向量机和神经网络都具有良好的分类能力。

1.1 支持向量机

支持向量机(Support Vector Machine, SVM)是由Vapnik于20世纪90年代最先提出的一种建立在统计学习理论基础上的机器学习算法[2],它可以分为分类型支持向量机(SVM for classification, SVC)和回归型支持向量机(SVM for Regression, SVR)。

令分类函数为:

f(x)=wTx+b

(1)

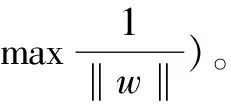
(2)

1.2 神经网络

误差逆向传播神经网络(Back Propagation Neural Networks, BPNN,简称BP)是一种包含三层(或三层以上)的多层前馈神经网络[3],在每一层中都有若干个神经元,左右相邻层之间的神经元相互连接,上下层的神经元没有连接,如图1所示。

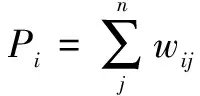
(3)

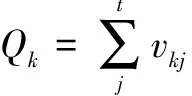
(4)

式(4)是神经网络计算得出的实际输出,如果与其期望的输出ok不一样或误差大不能满足要求,就需要对神经网络进行从后往前的网络校正,即通过改变隐含层、输出层的权值和阈值来实现。式(3)和(4)也可以认为是神经网络的数学模型,只是wij、θi、vkj和θk是未知的、动态变化的,需要在模型训练中计算得出。

图1 BP神经网络结构

2 SVR和BP在威胁判断中的应用原理

2.1 威胁判断模型设计

构建基于SVR或BP的对空威胁判断模型流程图,首先对训练数据、测试数据和待预测数据进行归一化处理,确保这些输入数据符合威胁评估模型的输入要求。然后用训练数据对威胁评估模型进行训练,使模型学习到训练数据之间包含的知识或规则,即各威胁因素与威胁值的对应关系;用测试数据对模型的准确性进行检验,即验证模型学习到的知识或规则是否准确、合理,如果准确性达到要求就分别得到基于SVR算法和BP算法的威胁值评估系统;最后使用该威胁值评估系统对新目标的威胁值进行预测,即把新目标的各因素取值输入到模型中,模型根据已学到的知识或规则,对新目标的威胁值进行评估,进而确定目标的威胁等级或进行威胁排序，其流程如图2所示。

图2 威胁判断模型流程

2.2 数据预处理

2.2.1 威胁因素确定

在水面舰艇对空威胁判断中,影响来袭目标威胁程度的因素众多,如果考虑所有的因素,并通过某个数学等式计算威胁值与各因素间的函数关系,难度特别大[4]。本文根据作战实际,选择以下六种典型的威胁因素作为威胁值评估系统的输入:航路捷径、目标类型、临舰时间、电磁信号、目标舷角、目标毁伤能力。其中航路捷径越小,导弹末制导雷达越容易搜索到我方舰艇,则目标威胁越大;临舰时间越短,留给我方舰艇作战准备的时间越少,我方受攻击的可能性越大,则目标威胁越大;如果收到导攻、制导等雷达信号,则目标威胁大,否则威胁小;敌舷角越小,目标越向我舰艇方向飞行,对我实施攻击的可能性越大,则目标威胁大。

2.2.2 数据归一化处理

由于不同威胁因素的单位不一样、各威胁因素的取值范围相差较大,为消除各属性之间不同量纲的影响,在对空中目标进行威胁判断时需要把所有数据转换成无量纲的纯数值数据,即对数据集按不同属性分别进行归一化处理,本文选用[1-2]归一化标准,其计算方法如下:

(5)

式(5)中x和y分别代表归一化前后的数据,xmin和xmax分别代表所有数据集中各属性的最大值和最小值,归一化后原始数据都被映射到的范围内。为得到准确的威胁值评估结果,需要把包括训练数据集、测试数据集和待预测数据集在内的所有数据当作一个整体,同时进行归一化处理,而不能对各训练集分别进行归一化处理。

2.3 模型的训练

模型的训练主要是让威胁值评估系统学习训练数据中包含的知识,即威胁值的评估规则;然后用测试数据对模型的准确性进行检验,把准确性最高的那组参数作为最优参数组。模型的预测是在训练好的威胁值评估系统上,用待预测数据作为模型的输入,威胁值评估系统根据之前学习的知识,对这些未知的空中目标进行威胁值预测。

2.3.1 基于SVR的对空威胁值评估模型

1)核函数选择和参数寻优

引入核函数后,提高了威胁判断模型的计算速度和准确性。常用的核函数包括高斯径向机核函数k(x1,x)=exp{-g‖x1-x‖2}、线性核函数k(x1,x)=x1Tx等,但在实际使用过程中,需要选择一个最优的核函数来解决特定的问题。常用的确定核函数的方法有以下两种:一是专家指定法,即特定领域的专家根据相关专业知识和经验,人为选择最优核函数;二是实验法,即利用Matlab等软件对常用核函数逐一实验,找到准确性最高、计算速度最快的核函数作为最优核函数。本文根据对空作战实际和经验,采用专家指定法,选择径向机核函数作为威胁值评估系统的核函数。

选择好核函数后,还要根据训练数据对模型的参数c、b和核函数的参数g进行确定,进而得到基于SVR的威胁值评估模型:

(6)

2)模型的训练步骤

根据专业知识和经验可以确定各参数的取值范围,也可以通过仿真实验确定各参数的大概取值范围。然后通过以下方法对模型进行训练:

①对参数c、b和g在各自取值范围内取某一值,取值的方法有可以用基于网格法、基于遗传算法或基于二分法等。由于本文的各参数取值不大,可以用网格法确定参数如何取值。为提高寻优的效率和准确性,寻优过程需要分两次进行：第一次粗选择,找到相对最优的概略范围;第二次概略范围内进行细选择,找到最优的参数组。

②用训练数据(假设N个样本)和测试数据(假设M个样本,通过N>M)对模型进行训练。为了提高模型的训练准确性和可靠性,对同一参数组可以进行多次(例如5次)训练,即把训练数据和测试数据合并一起(N+M个样本),随机选择N个样本作为训练数据,剩下的M个样本作为测试数据。经过多次训练,取准确性的平均值作为评价本参数组的性能。

③取上一步中准确性最高的参数组作为模型的最优参数组,代入式(2)就得到基于SVR的对空威胁值评估模型。

2.3.2 基于BP的对空威胁值评估模型

1)神经网络初始值的确定,权值wij、vkj和阈值θi、θk选取会影响到模型是否陷入局部最优值和模型的训练时间长短。在本文中取(-1,1)之间的随机数。

2)选择Sigmoid函数作为激活函数,按照式(3)对模型进行训练,求出模型的实际输出yk。如果yk-ok(k=1,2,…,m)不能满足要求,对权值和阈值的修正量Δwij、Δvkj、Δθi和Δθk进行修改,即从输出层经隐含层再到输入层,逐层修改权值和阈值,直到输出层所有神经元的实际输出值与期望输出值误差达到要求。

3)取上一步最后停止训练时的权值和阈值作为基于BP的对空威胁值评估模型的参数,代入式(4)得到输出层第k个输出的计算模型为:

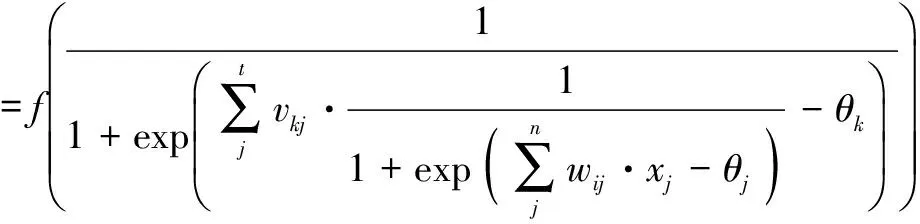
(7)

其中权值和阈值是动态变化的,即包含修正量Δwij、Δvkj、Δθj和Δθk。

3 模型仿真与比对

3.1 数据归一化处理

本文选取200批空中目标,为保证数据的准确性,各目标威胁因素值和威胁值由同一组专家在相同条件下给定。按照式(5)进行归一化处理后,得到威胁值评估模型可以直接使用的训练、测试和待预测数据集,部分数据如表1所示。

3.2 实例应用

利用Matlab软件对基于SVR和BP的对空威胁值评估模型(以下简称SVR模型和BP模型)分别进行仿真实验,仿真结果如图3、图4所示。

3.3 仿真结果分析

基于SVR和BP的威胁值评估模型有各自的优缺点:

1)SVR模型对未知数据的预测能力比较准确，而且结果稳定,所有威胁值误差大小都在0.3以内,如图3所示。

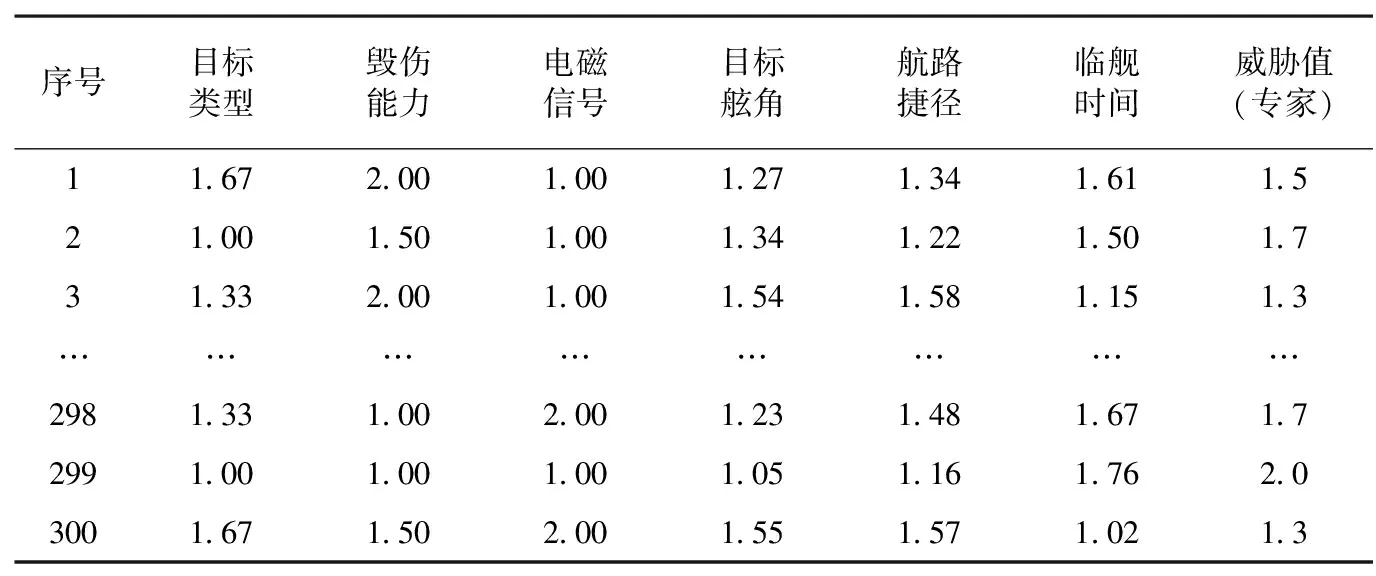
表1 预处理后的部分训练与测试数据

图3 基于SVR的对空威胁值评估仿真图

图4 基于BP的对空威胁值评估仿真图

2)BP模型对未知数据也有较好的预测能力,但是输出值不稳定。有时候准确性较高,误差大小在0.2左右,如图4(1);有时候准确性较低,误差大小在0.5左右,如图4(3)。

3)BP模型的训练时间比SVR模型的训练时间短,但相差不多。

导致以上结果的原因是多方面的,但主要由SVR和BP工作原理决定的。

首先SVR模型在小样本条件下进行训练时,也能很好地学习到输入数据与输出数据之间的非线性映射关系;而BP模型训练时需要提供大样本的训练数据,否则容易导致“欠学习”的情况发生。其次是SVR模型可以在全局范围内寻找到最优解,以提高对未知数据的预测能力;而BP模型很容易因权值和阈值的初始值选取不合适,导致“局部最优解”的情况发生。综合以上分析,SVR模型的准确性好、可靠性强。

在对空中目标进行威胁判断中,基于SVR和BP的威胁值评估模型可以提高威胁的灵活性和适应性,但是目前还无法提供大量的数据样本,所以为提高模型的稳定性和可靠性,应采用基于SVR的对空威胁值评估模型。

4 结束语

本文介绍了支持向量机和BP神经网络的基本理论;设计了威胁判断模型的流程图,确定了威胁因素和数据归一化标准,细化了SVR和BP模型的训练步骤。最后通过Matlab软件对两种模型分别进行了仿真,对仿真结果进行了分析,得出SVR模型更适用于当前对空威胁评估的结论。

[1] 张杰,徐志宇,王磊,等. 空间目标识别技术与威胁评估算法综述[J]. 机电一体化, 2011(3): 13-16.

[2] 方瑞明. 支持向量机理论及其应用分析[M]. 北京: 中国电力出版社, 2007.

[3] 史峰. MATLAB智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2015.

[4] 王玮,史红权,王磊等. 基于风险型多属性决策的编队空中目标威胁评估[J]. 舰船科学技术, 2014, 36(9): 146-149.

Application of Anti-air Threat Assessment Based on SVR and BP

WANG Fang1, ZHANG Jun-hui2, WU Zhi-quan1

(1.Dalian Naval Academy, Dalian 116018; 2.the Unit 91982 of PLA, Sanya 572000, China)

To improve the flexibility and adaptability of the anti-air threat assessment, the flow diagram of anti-air threat assessment is established based on Support Vector Machine for Regression (SVR) and Back Propagation Neural Networks (BP). The threat factors of anti-air threat assessment are selected, and the standard on normalization are ascertained. The training steps of the SVR models and BP models are detailed. An example is applied to the two models respectively, and the correctness of the conclusion is validated by Matlab. The advantages and disadvantages of the SVR models and BP models are analyzed, which concludes that the SVR models is more suitable for the anti-air threat assessment at the present stage.

support vector machine; neural networks; anti-air target; threat assessment

2016-10-31

2016-12-05

中国博士后科学基金项目(2014m562557)

王 芳(1979-),女,黑龙江哈尔滨人,硕士，研究方向为舰艇指控系统。 张军辉(1986-),男,助理工程师。 吴志泉(1986-),男,硕士。

1673-3819(2017)02-0051-04

TJ83；E072

A

10.3969/j.issn.1673-3819.2017.02.011