策略性等待下Y型瓶颈的单步拥堵收费模型

张梦婷，丁建勋,2，郑杨边牧，龙建成

(1. 合肥工业大学汽车与交通工程学院，安徽 合肥 230009；2. 合肥工业大学过程优化与智能决策教育部重点实验室，安徽 合肥 230009)

【交通运输】

策略性等待下Y型瓶颈的单步拥堵收费模型

张梦婷1，丁建勋1,2，郑杨边牧1，龙建成1

(1. 合肥工业大学汽车与交通工程学院，安徽 合肥 230009；2. 合肥工业大学过程优化与智能决策教育部重点实验室，安徽 合肥 230009)

本文针对包含至少一个上游瓶颈路段和一个共用的下游瓶颈路段的Y型交通路网，研究了策略性等待单步收费条件下早高峰期间通勤者的出行行为和最优道路拥挤收费方案。基于出行者的出发时间选择遵循用户均衡准则的假设，推导出了不同汇合规则下用户均衡的流入率和个人出行成本。依据出行者的出发时间选择规律，进一步推导出了最优的道路拥挤收费时段和费率。研究发现，策略性等待单步收费可以有效降低交通网络的系统总阻抗，但可能会增加出行者的个人出行成本。此外，还发现收费的有效性不但与汇合规则有关，还取决于上下游瓶颈路段通行能力的相对大小。该研究验证了Y型交通路网上存在Braess诡异现象，即扩大上游路段的瓶颈通行能力可能会引起系统总出行成本的增加。

道路拥挤收费；Y型瓶颈；策略性等待；单步收费模型；出发时间选择

随着城市化进程的加快，城市机动车拥有量不断增长，但与此同时城市道路的通行能力却无法随车辆的增加而扩充，两者之间的矛盾导致了严重的道路拥堵问题，影响着人们的工作和生活，也制约着城市的有效发展。

国外对交通拥堵问题研究的较早，Vickrey[1]于1969年首次应用确定性排队理论构建了单通道“经典瓶颈模型”，并运用模型计算出基于时间变化的收费方案以消除瓶颈处的排队。而后,许多学者针对这一开创性工作进行扩展研究，一方面，考虑到时变收费方案在现实中实施难度大，有些研究者开始寻找其替代方案[2-5]；另一方面，学者们对“经典瓶颈模型”中过于理想化的假设条件(如假设所有出行者是均质的、道路通行能力恒定不变、出行需求固定、仅存在单一瓶颈通道等)进行了修正，开始考虑出行需求变动[6]、出行者异质[7]、瓶颈路段通行能力变化[8-9]等。Kuwahara[10]首次建立了两个串联型瓶颈模型。Arnott等[11]分析了Y型通勤廊道中不允许晚到情况下的出行行为，研究发现Y型瓶颈模型中会出现Braess诡异现象，即上游瓶颈路段通行能力扩大将会使得系统总出行成本增大。

国内许多学者也就交通拥堵问题做了许多有意义的工作。Yang等[12]利用最优控制理论探讨了出行需求变动下的时变收费方案。朱广芹等[13]基于博弈论的分析方法，设计了基于博弈模型的拥堵收费算法。吴子啸等[14]从经典瓶颈模型入手，论述了道路系统达到最优使用状态的可能性及措施，由此提出了动态收费策略并讨论了该策略在我国道路系统中的应用。Xiao等[15]在单步拥堵收费方案下观察到出行者的策略性等待行为，并推导出此情形下最优的收费水平和收费时段。Xiao等[16]进一步扩展Arnott等[11]的研究成果，在考虑下游瓶颈路段通行能力随机变化的基础上，分析了两种不同汇合策略下出行者的出行行为。

综上所述，已有的研究主要集中于单一瓶颈模型假设条件的拓宽或拥堵收费策略的探讨，缺乏流量汇合的Y型通勤廊道的拥堵收费研究。本文基于已有研究成果，建立了策略性等待下Y型瓶颈的单步拥堵收费模型，通过研究Y型瓶颈通勤廊道早高峰期间出行者的出行行为，推导出最优的道路拥挤收费方案，并对方案的实施效果进行了验证。

1 Y型瓶颈模型简介

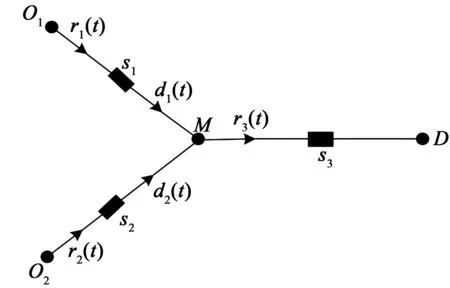
图1 Y型瓶颈模型结构图Fig.1 The structure diagram of Y shaped bottleneck model

与单一瓶颈模型[1]一样，我们在瓶颈处采用点排队模型，即不考虑车辆排队的物理长度。于是，t时刻瓶颈i处的排队长度可以表示为：

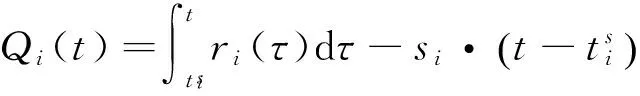
(1)

出行者从居住地到工作地的出行时间包括自由流走行时间和排队等待时间，其中，自由流走行时间与出发时间无关，为出行时间中的固定成分。不失一般性，我们假设每条路段的自由流走行时间为0。于是，各OD对出行者的总出行时间可表示为

(2)

不收费时，出行者的出行成本由出行时间成本和计划延误成本(上班早到或晚到的延误成本)两部分构成，即

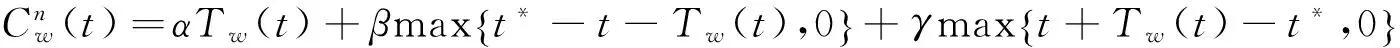
(3)

其中，α、β和γ分别为单位出行、单位早到和晚到时间费用。根据实证研究[17]有γ>α>β。

2 策略性等待单步收费下的均衡

由出行者的出行费用分析可知，出行者在不收费情形下需要在出行时间成本和计划延误成本之间做出权衡，选择最佳的出发时间以最小化个人出行费用。当没有出行者可以通过单边改变其出发时间来减小他的出行成本时，系统则达到用户均衡(UE)状态。在UE状态下，同一OD对的出行者具有相等且最小的出行成本。Xiao等[16]详细分析了GW和FR两种汇合规则下，下游路段瓶颈通行能力随机变化时出行者在UE均衡状态下的通勤出行行为。当瓶颈通行能力随机性降低为0时，可以得到确定性Y型瓶颈模型。

与不收费条件下的均衡分析一样[16]，我们分别研究GW和FR两种汇合规则下策略性等待单步收费对出行者均衡时的流入率及个人出行成本的影响，进而依据出行者的出发时间选择规律确定最优的道路拥挤收费时段和费率。

2.1 GW汇合规则

情形A1 :s1>s3

如图2所示，我们将从起点O1出发的出行者高峰出行时间划分为6段：(I)仅起点O1的出行者出行；(II) 起点O2的出行者开始出行；(III)收费开始前无出行者出行；(IV)起点O1的出行者在收费时段内出行；(V)起点O2的出行者完成出行；(VI)起点O1的出行者结束出行。下面就起点O1的出行者在各个阶段的出行行为进行分析。

图2 情形A1用户出行示意图(累计到达、离开)Fig.2 User equilibrium departures in case A1(cumulative arrivals and cumulative departures)

根据定义，我们有：

(4)

(5)

(6)

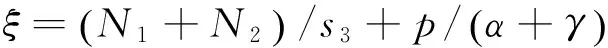
根据UE均衡准则，由(6)式可以得到策略性等待单步收费下出行者的个人出行成本：

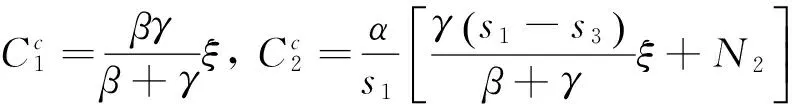
(7)

(8)

其中：

情形A2 ：s1≤s3

(9)

此外，起点O1的出行者的个人出行成本为：

(10)

与情形A1类似，可以求得最优的收费水平为：

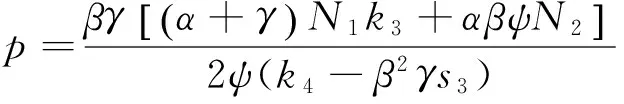
(11)

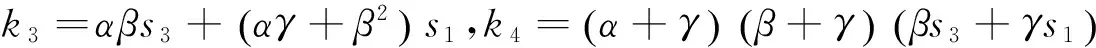
2.2 FR汇合规则

情形B1 ：s1>s3

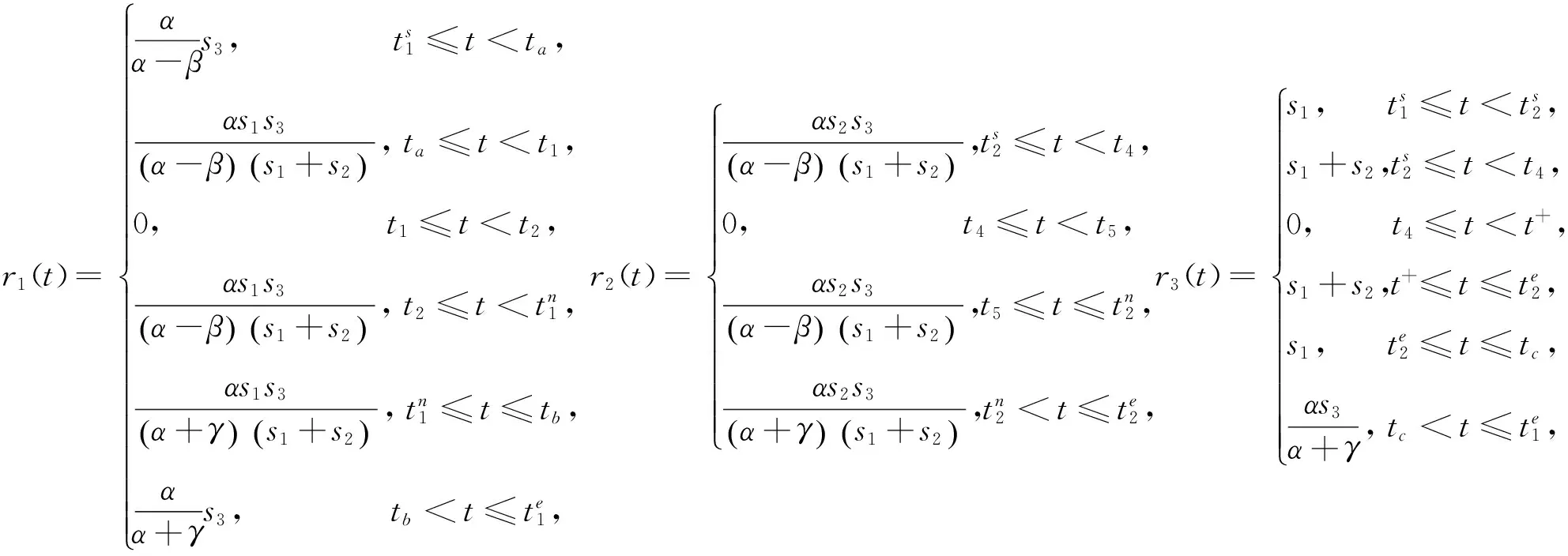
(12)

其中，t5为起点O2中第一个收费通过瓶颈3的出行者的出发时间。

受汇合规则影响，以下时间点的个人出行成本与情形A1有所不同:

(13)

根据(12～13)式，可以求解得到该情形下的临界时间点。结果表明除了以下时间点发生改变外，其他时间点与(6)式相同：

(14)

其中，φ=(α+γ)(s1+s2)-αs3。

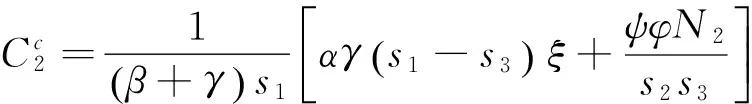
(15)

利用最优性条件可以推导出此种情形下最优的收费水平为：

(16)

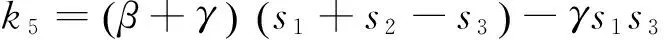
情形B2：s1≤s3

(17)

此时，起点O2的出行者的个人出行成本与同等条件不收费情形下保持相同。由(17)式可以求出起点O1的出行者个人出行成本为：

(18)

进一步利用最优性条件，可以得出此情形下最优的收费水平：

(19)

式中

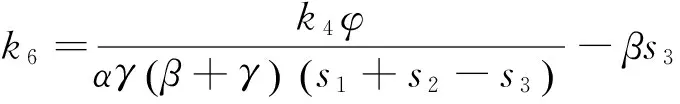
定理1 当s1>s3时，无论在哪种汇合规则下，策略性等待单步收费条件下两个OD对的出行者的个人出行成本较同等条件下不收费情形都有所增大，而系统总出行成本与不收费均衡相比则有所减小。

证明 在GW汇合规则下，根据(7)和Xiao等[16]的研究结果可得:

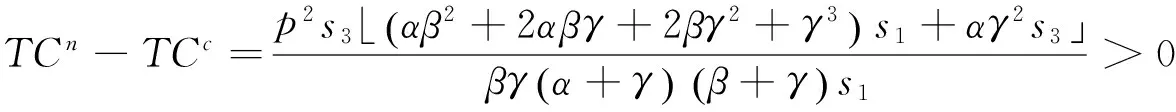
由此可判定TCn-TCc>0。

定理2 当s1≤s3时，无论在哪种汇合规则下，策略性等待单步收费条件下起点O2的出行者的个人出行成本与同等条件不收费情形相同，起点O1出行者的个人出行成本较同等条件不收费情形有所增大，而系统总出行成本与不收费均衡相比则有所减小。

此时，两种收费方案下系统总出行成本差值为

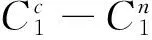
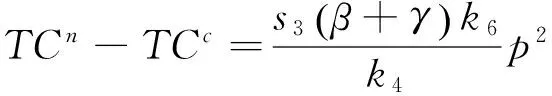
把φ和k4的表达式带入k6并整理，可得

由前面分析可知s1+s2-s3>0, 故k6>0, 从而TCn>TCc成立。

3 算例

本节采用一个数值算例来验证前面的理论分析结果。我们采用的模型参数设置为：N1=1 000(辆)，N2=500(辆)，α=6.4(元/时)，β=3.9(元/时)，γ=15.21 (元/时)，t*=9(时)，s2=800(辆/时)，s3=800(辆/时)。上游路段1的瓶颈通行能力分两种情况进行考虑：(1)s1>s3，s1=1 000(辆/时)； (2)s1≤s3,s1=800(辆/时)。

图3给出当s1>s3时，两种汇合规则下，上游路段的流入率随时间的变化情况。从图3可知，上游两个路段的流入率随汇合规则的不同而有所不同。在不收费的GW汇合规则下，路段2的流入率在其出行时间内恒定不变；而路段1的流入率随出行时间分段恒定。具体表现为：在高峰期前期r1(t)>s1，各瓶颈处的排队长度呈线性上升；在起点O2的出发时间段内，r1(t)=s1；高峰期后期r1(t)

图3 Y型交通路网上游路段的流入率Fig.3 The inflow rate of upstream bottleneck link in Y shaped traffic network

图4给出两种汇合规则下的个人出行成本和系统总出行成本随路段1的通行能力s1的变化关系。可以发现：当s1≤s3时，起点O1的出行者的个人出行成本随s1的增大而减小；当s1>s3时，起点O1的出行者的个人出行成本随s1的增大而增大。不同的是，起点O2的出行者的个人出行成本一直随s1的增大而增大；还可以观察到系统总出行成本的变化趋势取决于不同的汇合规则。当s1>s3时，在GW汇合规则可能会引起Braess诡异现象，即增大路段1的通行能力s1反而使得系统总出行成本增大。相反，在FR汇合规则下策略性等待收费策略能有效减小总出行成本。

图4 单步收费下的个人出行成本和系统总出行成本随上游路段1通行能力的变化情况Fig.4 Variation of the individual cost and system total cost with the change of capacity of upstream link 1 under the single-step toll

图5给出了两种汇合规则下，当s1=1 000(辆/时)时,两个OD对的出行者的个人出行成本和系统总出行成本随下游路段通行能力s3的变化关系。可以看到，无论在哪种汇合规则下，两OD对的个人出行成本和系统总出行成本都随下游瓶颈通行能力的增大而减小。因此，在策略性等待单步收费条件下扩大下游路段的瓶颈通行能力对于出行者个人和整个系统都是有益的。

图5 单步收费个人出行成本及系统总出行成本随下游路段3通行能力的变化情况 Fig.5 Variation of the individual cost and system total cost with the change of capacity of downstream link 3 under the single-step toll

图6给出了两种汇合规则下的策略性等待单步收费带来的系统总出行成本减少量随路段1的通行能力的变化关系。可以看到，扩大路段1的瓶颈通行能力有利于增强单步收费策略的实施效果。当路段1的通行能力较小时，GW汇合规则下实行单步收费对于缓解系统拥堵更为有效；但随着通行能力不断扩大，FR汇合规则对于减少系统总出行成本效果更为显著。

图6 系统总出行成本的减少量随上游路段1通行能力的变化情况Fig.6 Variation of the system total cost reductionwith the change of capacity of upstream link 1

4 结论

本文研究了早高峰期间Y型通勤廊道下游路段实行策略性等待单步收费时的出行者的出行行为，并给出了最优收费方案，以缓解由于通行能力限制带来的交通拥堵。基于Xiao等[16]设计的汇合规则，分析了不同汇合规则对用户出行行为的影响。在出行者的出发时间选择遵循用户均衡准则假设下，推导得到了不同的汇合规则下用户均衡的流入率、临界的时间点以及个人出行成本。在收费的刺激下，出行者通过调整出发时间以最小化个人出行成本，导致系统最早出发时间提前，最晚出发时间推后，从而使得整个早高峰出行时间延长。同时，进一步确定了不同汇合规则下的最优道路拥挤收费时段和费率。结果发现，与不收费均衡解相比，策略性等待单步收费方案可能会增大出行者的个人出行成本，但是能够有效降低系统总出行成本，本文的研究可以为制定合理的Y型交通路网上的道路拥堵收费策略提供理论依据。本文假设通行能力固定不变，且出行者都是均质的，这可能与实际情况存在一定差异，因此，今后将考虑出行者异质和随机通行能力等情况，以进一步优化此方案。

[1]VICKREY W S. Congestion theory and transport investment[J]. The American Economic Review,1969，59(2):251-260.

[2]ARNOTT R, de PALMA A, LINDSEY R. Departure time and route choice for the morning commute[J]. Transportation Research Part B: Methodological, 1990, 24(3):209-228.

[3]LAIH C H. Queueing at a bottleneck with single-and multi-step tolls[J]. Transportation Research Part A: Policy and Practice, 1994, 28(3):197-208.[4]LAIH C H. Effects of the optimal step toll scheme on equilibrium commuter behaviour[J]. Applied Economics, 2004, 36(1):59-81.

[5]LINDSEY C R, van den BERG V A C, VERHOEF E T. Step tolling with bottleneck queuing congestion[J]. Journal of Urban Economics, 2012, 72(1):46-59.

[6]ARNOTT R, de PALMA A, LINDSEY R. A structural model of peak period congestion: A traffic bottleneck with elastic demand[J]. American Economic Review, 1993, 83(1):161-179.

[7]RAMADURAI G, UKKUSURI S, ZHAO J,et al. Linear complementarity formulation for single bottleneck model with heterogeneous commuters[J]. Transportation Research Part B: Methodological, 2010, 44(2):193-214.

[8]LI H, BOVY P H, BLIEMER M C. Departure time distribution in the stochastic bottleneck model[J]. International Journal of Its Research, 2008, 6(2):79-86.

[9]LINDSEY R. Cost recovery from congestion tolls with random capacity and demand [J]. Journal of Urban Economics, 2009, 66(1):16-24.

[10]KUWAHARA M. Equilibrium queuing patterns at a two-tandem bottleneck during the morning peak[J]. Transportation Science, 1990, 24(3):217-229.

[11]ARNOTT R, de PALMA A, LINDSEY R. Properties of dynamic traffic equilibrium involving bottlenecks, including a paradox and metering[J]. Transportation Science, 1993, 27(2):148-160.

[12]YANG H, HUANG H J. Analysis of the time-varying pricing of a bottleneck with elastic demand using optimal control theory [J]. Transportation Research B: Methodological, 1997, 31(6):425-440.

[13]朱广芹, 佟光霁, 代磊磊. 城市道路交通拥挤收费的博弈分析[J]. 系统工程理论与实践, 2009, 29(7): 147-152.

[14]吴子啸, 黄海军. 瓶颈道路使用收费的理论及模型[J]. 系统工程理论与实践, 2000, 20(1):130-135.

[15]XIAO F, SHEN W, ZHANG H M. The morning commute under flat toll and tactical waiting[J]. Transportation Research Part B: Methodological, 2012, 46(10):1346-1359.

[16]XIAO L L, LIU R, HUANG H J. Stochastic bottleneck capacity, merging traffic and morning commute[J]. Transportation Research Part E: Logistics and Transportation Review, 2014, 64:48-70.

[17]SMALL K A. The scheduling of consumer activities: Work trips[J]. American Economic Review, 1982, 72(3): 467-479.

The single-step congestion toll model of Y-shaped bottleneck under tactical waiting

ZHANG Meng-ting1, DING Jian-xun1,2, ZHENG-YANG Bian-mu1, LONG Jian-cheng1

(1.School of Automative and Transportation Engineering, Hefei University of Technology, Hefei 230009, China; 2.Key Laboratory of Process Optimization and Intelligent Decision-Making Ministry of Education, Hefei University of Technology, Hefei 230009, China)

∶In this paper, according to the Y-shaped traffic network containing at least one upstream bottleneck and a common downstream bottleneck, the departure time choice behavior and the optimal road congestion pricing scheme during morning peak hours were investigated under tactical waiting and single step toll. Based on the assumption that the departure time choice followed the user equilibrium (UE) principle, the equilibrium departure rate and individual trip cost under different merging rules were derived. According to the departure time choice behavior, the optimal road congestion charging period and toll level were further derived. Research showed that the proposed pricing scheme could effectively decrease the total congestion of the traffic network system, however, it might lead to the increase in individual trip cost. In addition, it also found that the effectiveness of the proposed pricing scheme not only depended on the merging rules, but also depended on the relative magnitudes of the capacities of the upstream and downstream bottlenecks. Finally, the results showed that there was Braess paradox in the Y-shaped traffic network, which meant that the total system travel cost could be increased when the capacity of the upstream bottleneck was increased.

∶road congestion pricing；Y-shaped bottleneck；tactical waiting；single-step toll model；departure time choice

10.3976/j.issn.1002-4026.2017.02.011

2016-12-27

中国博士后科学基金(2014T70588，2013M530295)；国家自然科学基金(71201041，71371026， 71431003)

张梦婷(1992—)，女，硕士研究生，研究方向为交通拥堵收费。E-mail：18855170302@163.com

U491

A

1002-4026(2017)02-0067-11