基于改进粒子群算法的油料消耗量优化组合预测方法
2017-05-10雍歧东秦朝臻张晓峰
龚 杰,雍歧东,秦朝臻,张晓峰,刘 洲
(1.后勤工程学院 油料应用与管理工程系,重庆401311;2.96201部队,昆明 650200; 3.92403部队,福州350000)
● 基础科学与技术 Basic Science & Technology
基于改进粒子群算法的油料消耗量优化组合预测方法
龚 杰1,2,雍歧东1,秦朝臻3,张晓峰1,刘 洲1
(1.后勤工程学院 油料应用与管理工程系,重庆401311;2.96201部队,昆明 650200; 3.92403部队,福州350000)
油料消耗量预测是实施精确保障的关键环节,而预测精度是油料消耗量预测的重要评价标准。为提高预测精度,以GM(1,1)、平滑指数法(ES)及广义回归神经网络(GRNN)3种单一预测模型为基础,构建一种基于改进粒子群算法确定权重分配的优化组合预测模型。以某部队执行某任务的消耗量数据为依据,分别采用3种单一预测模型和基于改进粒子群算法的优化组合预测模型对油料消耗量进行拟合预测。结果表明:后者较前3种单一预测模型的拟合精度更高、预测误差更小,充分验证了该组合预测模型的可靠性和精确性。
油料消耗量预测;优化组合预测方法;粒子群算法
油料是重要的后勤保障物资,是武器装备发挥作战效能的动力源泉。随着作战样式的推陈出新,未来战争对油料的依赖性越来越强。如何准确预测油料消耗量,为确定油料储备、组织筹措调运、编配保障力量、实施精确保障提供决策依据,显得尤为重要。 油料消耗量通常是依据油料供应标准、任务持续时间、装备出动数量及装备出动频率等因素,凭经验大致估算,这种方法简洁高效,但主观性太强。近年来,灰色系统理论、小波分析、支持向量机、神经网络、粒子群算法、指数平滑等方法[1-4]被广泛应用于油料消耗量预测,取得了一定的预测效果,但这些单一模型预测的精度还不够高,预测数据波动较大。为此,有学者提出了优化组合预测模型[3-5],有效克服了单一模型的局限性,提高了预测精度,但又出现了组合预测模型最优权重难以选取的问题。目前,采用遗传算法、熵权法、层次分析法、粒子群算法等[6-9]来确定组合预测模型中各单一预测模型的权重,使得最优权重的选取更加可靠,提高了预测精度,但这些方法运算时间长、收敛速度慢、编程较复杂。
本文借鉴已有研究成果,对基本粒子群算法进行改进,构造基于改进粒子群算法的优化组合预测模型,通过算法求解,使得各单一模型的权重达到最优。最后,通过实例验证该优化组合预测模型的可行性、有效性及优越性。
1 粒子群优化算法
1.1 基本粒子群优化算法
粒子群优化算法[10](particle swarm optimi-zation,PSO)是由美国社会心理学家Kenned和电气工程师Eberhad于1995年共同提出的一种群体智能随机寻优算法。该算法模拟鸟群觅食行为,通过个体之间的竞争与合作来搜索复杂空间的最优解,具有简单易实现、收敛速度快、参数设置少等优点。
假设在一个D维的目标搜索空间中,由N个粒子组成一个种群G=(G1,G2,…,GN),其规模为N。向量X=(Xi1,Xi2,…,XiD)T为第i个粒子在搜索空间中的位置,也代表优化问题的一个潜在解。将Xi代入目标函数计算其适应度函数值,根据适应度函数值的大小来衡量Xi是否为最优解[11]。向量V=(Vi1,Vi2,…,ViD)T为第i个粒子的速度,向量Pi=(Pi1,Pi2,…,PiD)T为第i个粒子迄今为止搜索到的最优值,向量Pg=(Pg1,Pg2,…,PgD)T为群体搜索到的最优值。
粒子按照下列公式来更新自身的速度和位置,以此来实现迭代寻优。即:
(1)
(2)
式中:i=1,2,…,N;d=1,2,…,D;k为当前迭代次数;Vid为粒子的当前速度;c1和c2为加速因子,是非负的常数;r1和r2是服从[0,1]均匀分布的随机数;ω为惯性权重。
1.2 改进粒子群优化算法
在粒子群算法中,粒子是向自身历史最佳位置和群体历史最佳位置聚集,形成粒子种群快速趋同效应,容易陷入局部寻优、早熟收敛等现象[12],同时,粒子群算法的精度和效率与惯性权重ω及加速因子c密切相关。因此,本文就从这两个系数入手来改进基本粒子群算法。
1.2.1 改进惯性权重
惯性权重ω会影响算法的收敛性,其大小决定了粒子对当前搜索速度的保留程度。文献[12]建议ω的取值随迭代次数的增加,从0.9线性递减至0.4。ω取值越小,粒子速度和粒子位置更新的幅度就越小,粒子会继续原来的搜索轨迹进行细部搜索,有利于小范围内寻优,加速算法收敛,提高搜索精度,但容易陷入局部最优;ω取值越大,粒子速度和粒子位置更新的幅度就越大,粒子会偏离原来的搜索轨迹进行搜索,有利于大范围内寻优,提高全局搜索能力,但收敛速度较慢。
为平衡该算法的局部寻优能力和全局搜索能力,通过调整ω的大小来控制上一次搜索速度对当前搜索速度的影响。因此,本文构造如下函数来更新惯性权重,其变化公式为
(3)

1.2.2 改进加速因子
加速因子c1和c2是调整自身学习能力和群体协作能力在搜索过程中的比重,通常取c1=c2=2。文献[10]也提出c1和c2随迭代次数增加而线性改变的方法。如果c1=0,就只有群体协作能力,而没有自身学习能力,此时容易陷入局部最优;如果c2=0,就只有自身学习能力,而没有群体协作能力,此时很难搜索到最优位置。c1=c2=2的设置不能体现粒子自身学习能力和群体协作能力随迭代次数的变化而变化,且在寻优过程中,粒子自身学习能力和群体协作能力是一个非线性变化的过程,加速因子c1和c2的线性改变不能体现这种变化。
在理想状态下,迭代初期应使粒子尽可能地进行全域搜索,这就要求粒子自身学习能力大一些,迭代后期应尽量避免陷入局部最优,这就需要粒子群体协作能力大一些,也就是随着迭代次数的增加,c1逐渐减小,而c2逐渐增大。基于以上考虑,本文采用tan函数构造的非线性函数来改进加速因子,设置最大默认的加速因子为2,构造单调递减函数c1,单调递增函数c2,其表达式为
(4)
1.3 改进粒子群算法求解步骤
用改进粒子群算法求解优化组合预测模型中各单一预测模型的权重,可通过Matlab软件编程来实现。
步骤1:选定改进粒子群优化算法的种群规模N、最大迭代次数Tmax、最大惯性权重ωmax、最小惯性权重ωmin等相关参数。
步骤2:随机初始化粒子的速度和位置。其中粒子的位置代表优化组合预测模型中各单一模型的权重。
步骤3:计算每个粒子的适应度函数值fitness(i)。
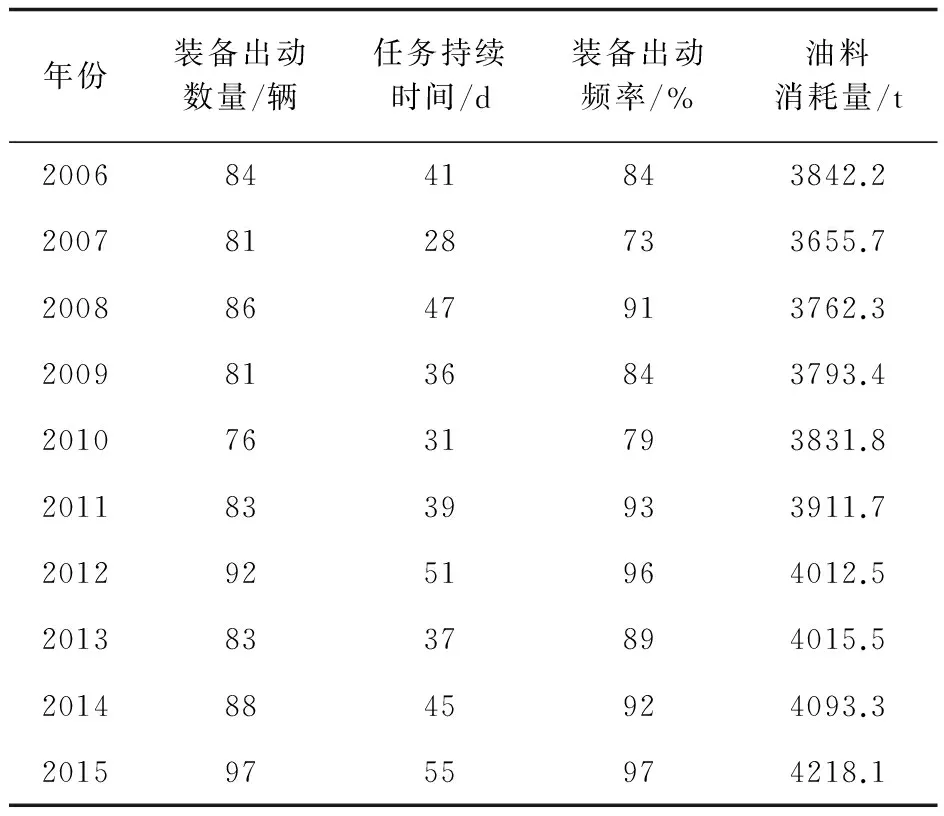
步骤4:比较计算适应度函数值fitness(i)与粒子当前最优值fitnessPbest的大小,若fitness(i) 步骤5:比较所有粒子的最佳适应度函数值fitnessPbest与当前的全局极值fitnessGbest,如果fitnessPbest 步骤6:按照式(3)和式(4)更新惯性权重和加速因子,再根据式(1)和式(2)更新粒子的速度和位置。 步骤7:判断当前迭代次数是否达到最大迭代次数Tmax。若不是,则返回步骤3进行下一次迭代;若是,输出fitnessGbest和Gbest。 2.1 组合预测模型 组合预测模型是将两种及以上的单一预测模型进行组合,通过某种方法为各单一预测模型分配权重。其数学模型为 (5) 为得到最佳的组合预测结果,就需要为各单一预测模型分配权重。本文以均方误差MSE(即误差平方和的平均数)最小为目标函数,来求解和优化各单一预测模型的权重ωi。即 (6) (7) 当均方误差(MSE)取得唯一最小值时,ωi即为优化组合预测模型中各单一预测模型的最优权重。 2.2 确定优化组合预测模型权重 以式(6)为适应度函数,式(7)为约束条件,按照改进粒子群算法的7个求解步骤,求出的fitnessGbest即为优化组合预测模型的均方误差MSE,Gbest即为各单一预测模型的权重ωi,代入式(7)即可求出优化组合预测模型的预测值。 某部队执行某任务的油料消耗量数据(经脱密处理)见表1。 表1 某部队执行某任务的油料消耗量数据 某部队执行某任务的油料消耗量受任务持续时间、装备出动数量、装备出动频率等诸多因素的影响,鉴于数据本身具有非线性、随机性、复杂性等特点,本文选用GM(1,1)、广义回归神经网络(GRNN)、指数平滑法(ES)这3种单一模型来预测历年油料消耗量,并建立优化组合预测模型来预测该部队历年执行某任务的油料消耗量。 3.1 GM(1,1)预测模型 灰色预测模型是基于原始数据累加生成序列并建立指数模型来实现数据预测与拟合[13]。GM(1,1)为一阶且只含一个变量的微分方程预测模型,主要用于时间序列预测,具有运算简便、易于检验,不用考虑分布规律和变化趋势等优点。本文根据文献[5,13]的分析,利用Matlab仿真软件编写求解程序,将表1中历年的油料消耗量作为输入数据,得到预测值与真实值的曲线拟合如图1所示,预测数据见表2。 图1 GM(1,1)模型预测值与真实值的曲线拟合 3.2 广义回归神经网络预测模型 广义回归神经网络(GRNN)是一种基于非线性回归理论的前馈式神经网络模型,由输入层、模式层、求和层和输出层组成,有着较强的非线性映射能力和柔性网络结构,且逼近能力、分类能力及学习速度较强[14]。GRNN只需给出对象的输入样本,通过网络自身训练,就能达到输入与输出的映射关系。 表2 各预测模型预测值与真实值的对比 本文借鉴文献[14-15]的研究思路,选取装备出动数量、任务持续时间、装备出动频率作为输入变量,油料消耗量为输出变量,以2006—2014年油料消耗量数据为网络训练样本,2015年的油料消耗量数据为外推测试样本。当spread=0.7时,训练数据的预测效果较好,得到预测值与真实值的曲线拟合如图2所示,预测数据见表2。 图2 GRNN预测值与真实值的曲线拟合 3.3 指数平滑预测模型 油料消耗量随时间变化波动,其数据分布无规律、较分散,很难用线性关系来表示。而指数平滑法则认为时间序列的态势具有稳定性和规则性[12],它是通过前期真实值的加权来表示预测值,对不同时期的历史数据赋予不同的权重[16],远期数据赋予较小的权重,近期数据赋予较大的权重。 本文采用二次指数平滑法预测油料消耗量,以预测值与真实值的均方误差MSE最小来选取平滑指数α。设油料消耗量的时间序列为y1,y2,…,yt。 则一次、二次指数平滑值为 (8) t+T年的预测值为 (9) 将表1中历年的油料消耗量作为输入数据,利用Matlab仿真软件编程求解。经过多次试算,当α=0.393时,预测值与真实值的均方误差MSE最小,此时的曲线拟合如图3所示,预测数据见表2。 图3 指数平滑预测值与真实值的曲线拟合 3.4 优化组合预测模型 针对以上3种单一预测模型精度不高,数据波动较大等问题,基于以上3种单一预测模型构造组合预测模型,并采用改进粒子群算法求解并优化各单一预测模型的权重。按照改进粒子群算法的求解步骤,在Matlab中编程求解。设置种群规模N=30,粒子维数D=3,最大迭代次数Tmax=200,最大惯性因子ωmax=0.9,最小惯性因子ωmin=0.4。以式(6)为约束条件,以式(7)为适应度函数,适应度函数值即为均方误差MSE。求解得到最优粒子的位置为(0.255 4,0.179 7,0.564 9),分别对应GM(1,1)、指数平滑、广义回归神经网络3种单一预测模型的权重,将其代入式(5),求出组合模型的预测值见表2,此时的曲线拟合如图4所示。算法迭代过程的适应度曲线如图5所示,基本粒子群算法迭代到100次时,得到适应度函数值(即均方误差MSE)为95.288;而改进粒子群算法迭代到18次时,得到适应度函数值为69.017。对比可发现,改进粒子群算法减少了迭代寻优次数,提高了预测精度。 图4 组合模型预测值与真实值的曲线拟合 图5 迭代过程的适应度曲线 3.5 预测结果评价 为评价优化组合预测模型的预测效果,本文引入平均相对误差(MAPE)和均方误差(MSE)两个指标加以评价。 表3是利用上述指标评价各模型的预测效果。 表3 各预测模型预测效果对比 由表3可知,改进PSO优化组合模型的平均相对误差(MAPE)和均方误差(MSE)远远小于GM(1,1)、ES、GRNN这3种单一预测模型。表明该优化组合预测模型拥有较高的预测精度,为部队准确预测油料消耗量提供了理论依据和实践参考。 (1)本文构建基于改进粒子群算法确定单一预测模型权重的优化组合预测模型,并将其用于某部队执行某任务的油料消耗量预测,充分证明该优化组合预测模型的可行性。 (2)本文对比分析各模型的预测结果(见表2),改进粒子群优化组合预测模型大大减小了预测误差,验证了该优化组合预测模型的可靠性和精确性。 (3)由图5和表2可知,改进粒子群算法在寻优能力、收敛速度及预测精度等方面要优于基本粒子群算法,体现了改进PSO优化组合预测模型的优越性和普适性。 [1] 张德亮,杨国利,郭嘉,等.小波分析在油料消耗预测中的应用[J].军事交通学院学报,2014,16(11):86-90. [2] 陆思锡,周庆忠,熊彪.基于支持向量机的舰艇部队作战油料消耗量预测研究[J].物流技术,2013,32(3):468-470. [3] 夏秀峰,刘权羲.基于灰色神经网络的装甲部队油料消耗预测[J].火力与指挥控制,2014,39(9):91-100. [4] 周庆忠,曾慧娥.基于改进微粒群神经网络的油料储备预测[J].计算机仿真,2013,30(9):314-315. [5] 倪聪,周庆忠,刘磊,等.基于GM-SVM的边境封控油料保障需求预测[J].军事交通学院学报,2016,18(3):90-94. [6] 都国兵.基于遗传算法的变权重组合预测模型研究及应用[D].兰州:兰州大学,2011. [7] 詹斌,吕腊梅,黄馨.基于熵权法的公路货运路组合预测[J].物流技术,2013,32(3):468-470. [8] 黄家亮,何宏,杨军.基于层次分析法的军队油料消耗组合预测模型[J].后勤工程学院学报,2009,25(2):83-87. [9] 贾义鹏,吕庆,尚岳全.基于粒子群算法和广义回归神经网络的岩爆预测[J].岩石力学与工程学报,2013,32(2):343-348. [10] 魏秀业,潘宏侠.粒子群优化及智能故障诊断[M].北京:国防工业出版社,2010. [11] 马军杰,尤建新,陈震.基于改进粒子群优化算法的灰色神经网络模型[J].同济大学学报,2012,40(5):740-743. [12] 余胜威.MATLAB优化算法案例分析与应用[M].北京:清华大学出版社,2014. [13] 司守奎,孙玺菁.数学建模算法与应用[M].北京:国防工业出版社,2013. [14] 张德丰.MATLAB神经网络应用设计[M].北京:机械工业出版社,2012. [15] 史峰. MATLAB智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011. [16] 曹军海,杜海东,陈小龙,等.基于平滑指数仿真优化的装甲装备器材消耗预测[J].系统仿真学报,2013,25(8):1961-1965. (编辑:史海英) POL Consumption Optimal Combination Forecast Method Based on Particle Swarm Optimization GONG Jie1,2, YONG Qidong1, QIN Zhaozhen3, ZHANG Xiaofeng1, LIU Zhou1 (1.Military Oil Application and Management Engineering Department, Logistical Engineering University,Chongqing 401311, China; 2.Unit 96201, Kunming 650200, China; 3.Unit 92403, Fuzhou 350000, China) POL consumption forecast is the key link in precise support, and forecast accuracy is the important evaluation index of POL consumption forecast. In order to improve forecast accuracy, this paper firstly establishes an optimal combination forecast model with improved particle swarm optimization to determine weight distribution on the base of three single forecast models: grey model(GM) (1, 1), exponential smoothing(ES) and general regression neural network(GRNN). Then, it forecasts POL consumption with three single forecast models and optimal combination forecast model based on improved particle swarm optimization respectively according to the consumption data of a troop. The result shows that the optimal combination forecast model has higher fitting accuracy and the less forecast error compare with three single forecast models, which has proved the reliability and accuracy of this combination forecast model. POL consumption forecast; optimal combination forecast method; particle swarm optimization 2016-11-23; 2016-12-20. 全军军事类研究生资助课题(2013JY366). 龚 杰(1989—),男,硕士研究生; 雍歧东(1964—),男,教授,博士研究生导师. 10.16807/j.cnki.12-1372/e.2017.04.020 E233 A 1674-2192(2017)04- 0084- 062 改进粒子群算法确定优化组合预测模型的权重
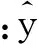
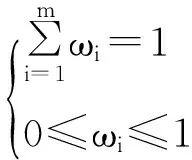
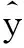
3 实例应用
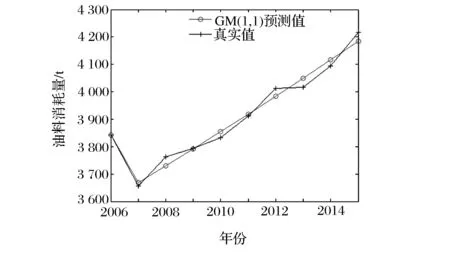

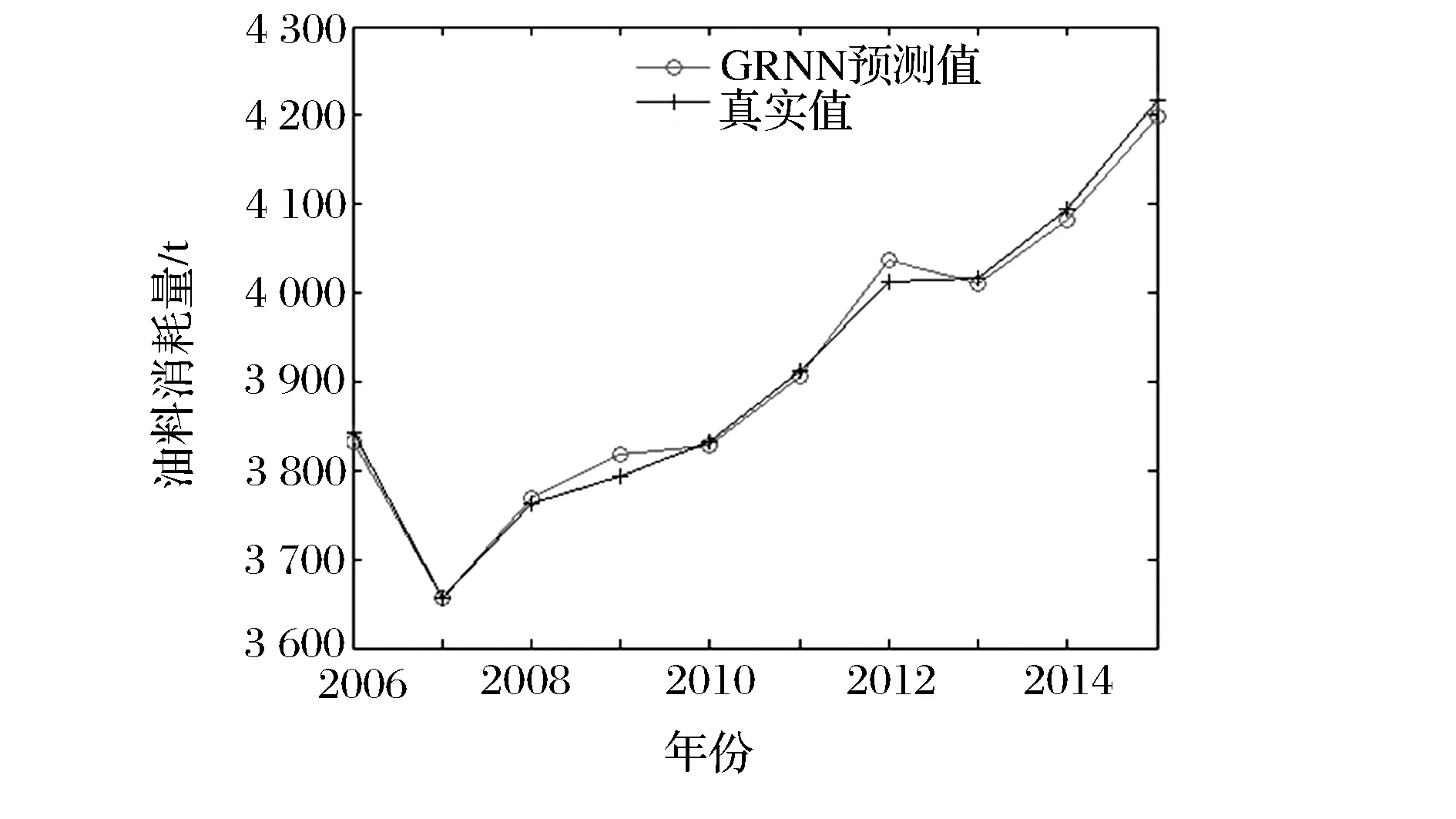
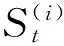

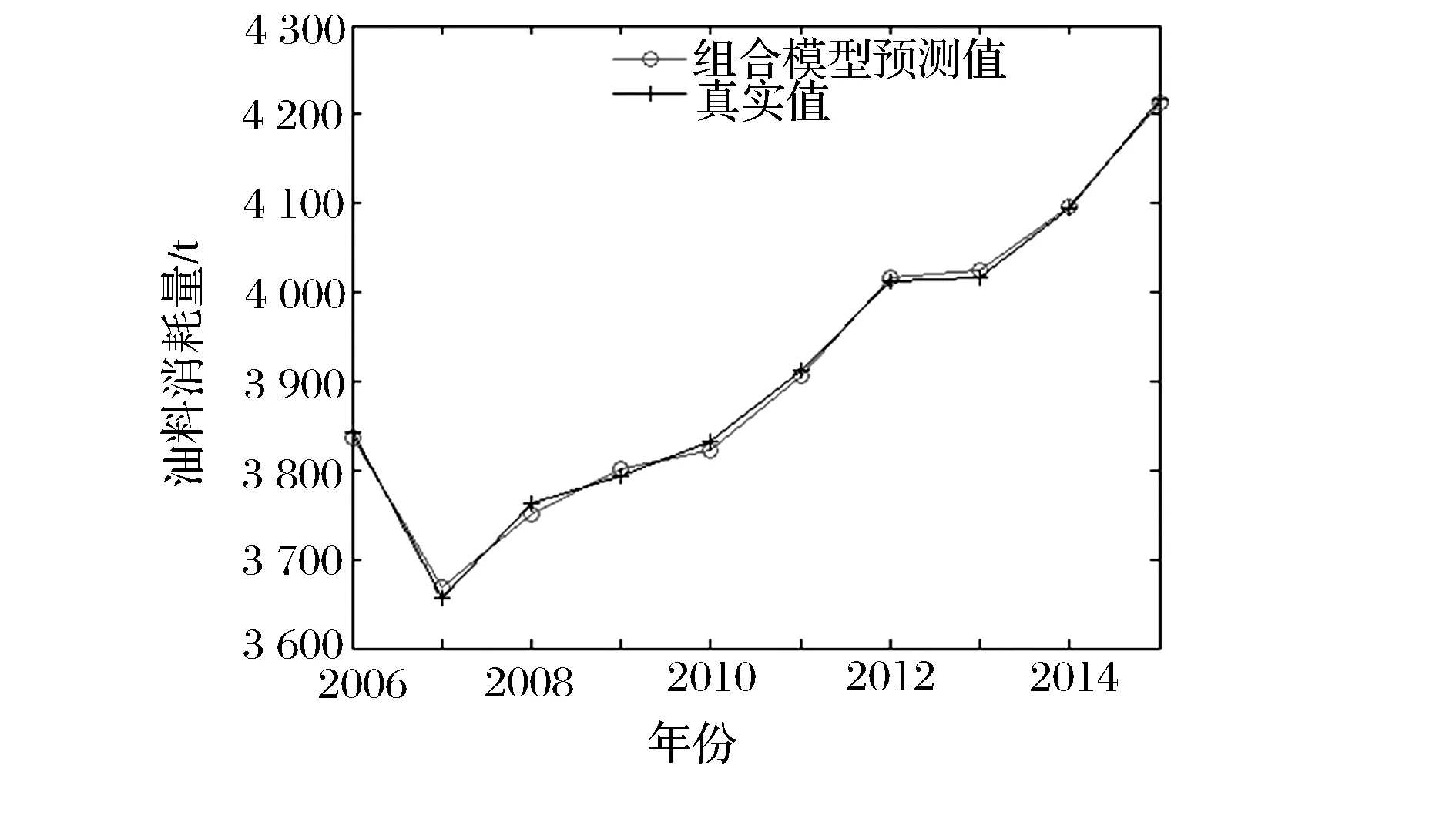
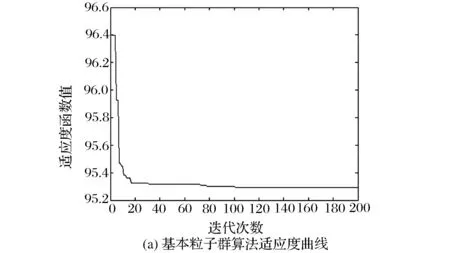

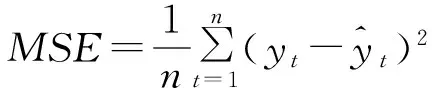
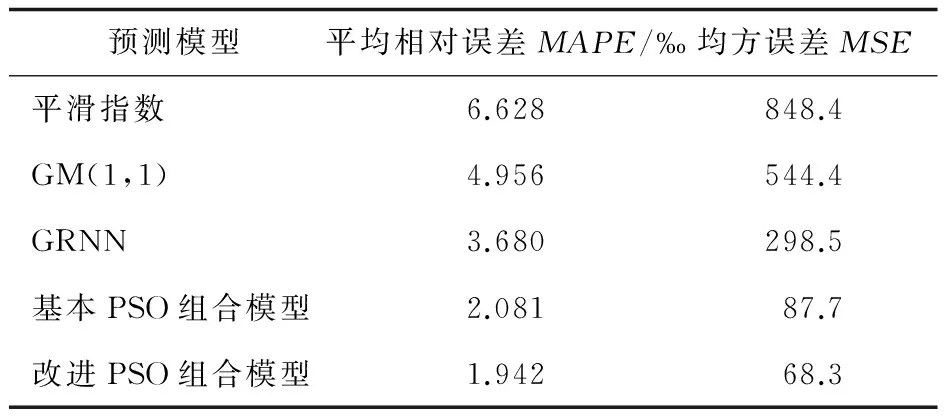
4 结 论
