研究型教学在军事运筹学教学中的探索实践

陈淑珍，钟 敏，陈博文

(军事交通学院 基础部，天津 300161 )



● 教育训练 Education & Training

研究型教学在军事运筹学教学中的探索实践

陈淑珍，钟 敏，陈博文

(军事交通学院 基础部，天津 300161 )

通过在军事运筹学的教学中采用研究型教学模式，探索“课内理论—课外研究”的具体教学方式。从线性规划理论的一个具体下料问题案例的教学应用、优化实现与结论研讨的角度，探索和实践在教学中采用研究型教学模式的设计原理、实施过程、注意事项，从而培养学员的科研素养及提高学员对知识的渴求和兴趣。

研究型教学；线性规划；建模求解

研究型教学是指教师以问题研究的形式组织教学，学员在研究中获得知识和研究方法的教学模式。研究型教学[1]是目前高等教育教学发展的重要方向，对培养满足社会需求的高级应用型创新人才，具有十分重要的意义。

研究型教学旨在通过教学与研究的结合，在教员指导下，学员以个人或团体为主体，自主地学习、探索、思考，从而调动学员学习的积极性，引导学员获取创造性运用知识的经验，教学目的不仅仅是使学员获得知识，更重要的是培养学员的创新意识、批判性思维等科研素养。在基础和专业基础课程的教学中，由于课程内容距离实际应用较远且学时紧张，具体实践研究型教学并不容易[2-4]。笔者在军事运筹学课程教学中，创造性地进行了“课内理论—课外研究”的研究型教学的尝试，并将尝试的过程与结果进行了梳理和总结。

1 课内理论及案例讨论

1.1 线性规划模型及其建立

在军事后勤的指挥和管理中，经常会提出一类问题，即如何合理利用有限的人力、物力、财力等资源，以便达到最好的军事效果。这类问题[5]都可以用一组决策变量(x1，x2，…，xn)表示某一方案；决策方案都受到一定的限制，这些限制条件可以用决策变量的一组线性等式或线性不等式来表示，称之为约束条件；都有一个要求达到的目标，它可以用决策变量的线性函数来表示，称之为目标函数。满足以上3个条件的数学模型称为线性规划的数学模型，其一般形式为

一般地说，建立线性规划问题的数学模型应包括3个步骤：一是分析问题。应先搞清楚实际问题的背景，抓住主要矛盾，明确该问题所要实现的目标与受到的限制。为了建模方便，可以将已知的条件列成表格形式。二是将问题中关键的、可以控制的量设为决策变量，然后将问题的限制条件表示成决策变量的线性等式或不等式，同时还要注意决策变量是否受到非负约束，构成问题的约束条件。三是明确所要求的目标是求最大值还是求最小值，将其表示成决策变量的线性函数——目标函数。

1.2 下料问题案例的讨论

某工程分队需要做某种钢架100套，每套用长2.9 m、2.1 m和1.5 m的相同规格的圆钢各1根。已知原材料长7.4 m，问应如何下料，使用的原材料最省。

案例分析：原材料7.4 m，如果截取2.9 m、2.1 m、1.5 m的各1根，余0.9 m。做100套钢架需用100根原材料。引导学员思考，如果想节省原材料，不能采取单一的下料方案，而应寻找尽可能多的套裁下料方案。经课堂讨论给出8种较好的套裁方案(见表1)。

模型建立：设第i种套裁方案下料xi(i=1,2,…,8)根为决策变量，以各规格的圆钢数达到要求为约束，以总根数最小为目标，建立模型为

表1 所有套裁下料方案

minz=x1+x2+x3+x4+x5+x6+x7+x8

以课堂案例引导学员进一步思考讨论5个方面的问题：一是如何寻找所有的下料方案， 如何求得最优解决方案；二是约束中“=型”和“≥型”的约束是否有区别；三是“料头和”与“根数和”作为目标函数哪个更合理；四是不同目标应怎样与不同类型的约束结合，怎样找到更确切的模型；五是实际中还有哪些问题需要注意。

2 课外研究——问题的实际延伸及研究实践

2.1 研究案例及设计原理

研究案例：某部需为工兵分队建造100副专用钢架。每副钢架需用同种材料的角钢，1.5 m的2根，1.45 m的2根，1.36 m的6根，0.35 m的12根。若现有的角钢原材料每根长为8 m，请给出优化的解决方案。

这个问题作为研究型教学案例是因为它既是课堂教学的延伸，又复杂于课堂案例。在研究型教学案例的设计上遵循的是“跳一跳，摘到桃”[6]的原理。研究型教学案例设计的关键是案例研究的难度，教员把握好这个度，才能提高学员的“跳跃”能力。“桃子”不是一伸手就能摘到，要摘到必须“跳一跳”，学员必须通过自己的一番努力而摘到“桃子”，才会带给他们一种自豪感和成就感，进而激发他们继续解决问题的欲望。同时，问题的难度又不能够太大，就是说只要学员努力地去“跳”，或者借助于“梯子”等工具，“桃子”应该是可以够得到的，否则，学员将会失去奋斗的动力。

2.2 研究案例的研究实践过程

这个问题看似与课堂上讨论的案例一样，但由于它截取的材料较短，而原材料的长度又比较长，使得套裁的方案会很多，如何寻找套裁方案而达到优化的目的就成为难题。要求学员在两天时间内分组讨论、建模求解，汇报解决问题的思路、方法和结论。

在实施中，由于套裁方案众多，学员普遍把套裁方案的料头小于最小材料的长度(0.35 m)作为判断套裁方案是合理方案的标准，不再考虑料头长度达到或超过0.35 m的方案。同时，为了寻找最优的下料方案，学员使用了多种方法。

(1)第1种思路。考虑所需的角钢有3种尺寸接近：1.5 m、1.45 m、1.36 m，称其为长角钢；另一种0.35 m的，称其为短角钢。所以尽量先截取长角钢(3种)，然后利用余料截取短角钢，且考虑短角钢需求较多，不足部分需用整根原材料截取(1种)，从而做出下料方案(见表2)。

表2 “3+1”下料方案

设第i种方案下料xi(i=1,2,3,4)根为决策变量，以各规格的角钢数达到要求为约束，以总根数最小为目标，建立模型

minz=x1+x2+x3+x4

求解，得出使用原材料233根。

(2)第2种思路。学员觉得寻找所有方案有困难，并发现有一种套裁方案没有料头。即一根原材料可正好截取1.5 m和1.45 m角钢各两根，0.35 m角钢6根。

受工程所需的1.50 m和1.45 m各200根的总数限制，先拿出100根原材料按该方案截取，可得1.5 m和1.45 m各200根，0.35 m的600根。然后只需考虑截取1.36 m和0.35 m的两种规格的材料，方案就容易寻找了，共有6种方案(见表3)。

表3 两种规格角钢下料方案

设第i种方案下料xi(i=1,2,…,6)根为决策变量，以两种规格的角钢数达到要求为约束，以总根数最小为目标，建立模型

minz=x1+x2+x3+x4+x5+x6

求解，得出使用原材料131根。

综合前面的100根，最终使用原材料231根。

(3)第3种思路。利用枚举法列出下料方案的学员最多，但限于列举方法和耐性，大家列出的下料方案数参差不齐，所以得到的使用根数也不尽相同。设第i种套裁方案下料xi(i=1,2,…,k)根为决策变量，以各规格的角钢数达到要求为约束，以总根数最小为目标，建立模型

其中ai，bi，ci，di(i=1,2,…,k)分别表示在第i种套裁方案中截取1.50 m、1.45 m、1.36 m和0.35 m的根数，求解。学员中最多的列出了所有的56种下料方案，得出使用原材料229根。方案不齐的，一般得不到这么好的结果。

(4)第4种思路。学员运用了计算机课程中二叉树的知识寻找下料方案，共列出了56种方案。设第i种方案下料xi(i=1,2,…,56)根为决策变量，以各规格的角钢数达到要求为约束，以总根数最小为目标，建立模型

式中：aij(i=1,2,3,4;j=1,2,…,56)分别表示第i种所需角钢( 1.50 m、1.45 m、1.36 m和0.35 m)在第j种套裁方案中截取的根数；bi(i=1,2,3,4)分别为4种角钢所需的总数200根、200根、600根和1 200根，求解得出使用原材料229根。

(5)第5种思路。利用选修课matlab数学软件寻找下料方案。考虑针对每根原材料(8 m)的截取应满足下面约束

约束中的yi(i=1,2,3,4)分别表示一根8 m原材料能截取1.50 m、1.45 m、1.36 m和0.35 m的根数，y5表示所剩的料头。用matlab编程计算，也得出全部56种下料方案。

设第i种方案下料xi(i=1,2,…,56)根为决策变量，以各规格的角钢数达到要求为约束，以总根数最小为目标，建立模型求解，得出使用原材料229根。

3 “课内—课外”研究型教学对课堂教学的提升

3.1 优化理论的实现——线性规划软件的运用

课堂教学中，模型的建立、解决理论与方法的教学，都是以一些比较小的问题为例进行的，这时教学的重点是理论与方法的理解，如果把课内案例搞得太复杂，会冲淡主要教学目标，降低学员对理论与方法本质的理解程度。

但实际问题往往是比较复杂的，至少规模是比较大的，此时利用手算往往是不可能实现的，此研究案例的求解过程中，不管哪一种思路，学员建立的线性规划模型，用课堂上讲的单纯形法手工计算都是很复杂的，模型中最多的有56个决策变量，还需4个松弛变量，4个人工变量，这就要求学员用所学的运筹理论方法建立模型，利用软件Lindo或Lingo实现求解。这个研究型案例的解决过程，提升了课堂教学中求解理论到现实实现的飞跃。求出的最优下料方案见表4。

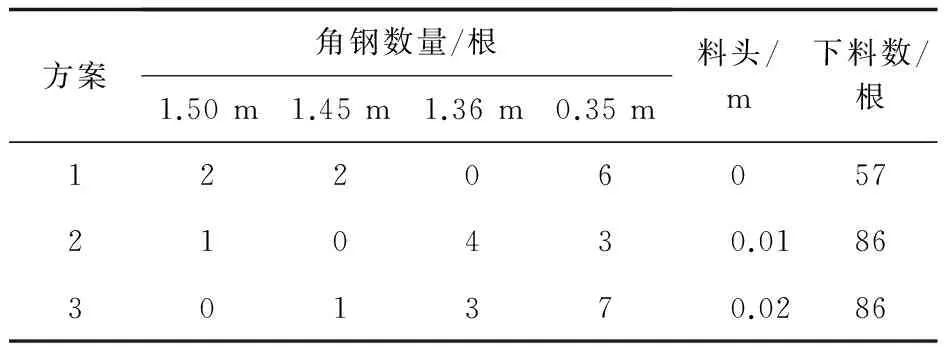
表4 最优决策的下料方案及根数

3.2 优化思想的完善——局部优化与全局优化

“课内—课外”研究型教学，首先让学员建立了优化的意识，并通过课内理论掌握了优化的方法，课外研究实现了优化的目标，这个研究型案例的解决过程也暴露了学员优化思想理解中的偏差。对2013—2016年度学习运筹学学员的案例研究的思想、方法、模型和结论进行分析汇总(见表5)，发现第2种思路中，学员认为第一步100根料头为0的截取方法应是最优的，第二步两种规格角钢的下料方法全都考虑了，也是最优的，所以采用两步下料方法，用料一定为最少的。但通过多种思路的讨论、计算、比较，看到第2种思路中给出的结果并不是最优的，这点很好的说明在实际问题中，局部优化不一定达到全局优化。这个研究型案例的解决过程提升了课堂教学中优化思想的高度。

表5 案例研究数据汇总

3.3 优化方法的实践——优化意识在现实中的灵活实践

从计算结果的进一步讨论中发现，一共有56种下料方案，但表4最优决策中只用了3种，依次是料头0 m、0.01 m、0.02 m最少的3种。所以在实际问题中，分析下料方案时，可以不求出所有方案，而只考虑料头在限制范围内的方案，问题会变得简洁，也可以得到比较优的结果。所以由Matlab数学软件计算时，可变更约束为

式中r为套裁方案对料头的要求。经计算得出结果：r为0.05，即料头小于0.05 m的套裁方案9种；r为0.1，即料头小于0.1 m的套裁方案16种；r为0.2，即料头小于0.2 m的套裁方案24种，3种情况下建立模型、求解，得到的最优解决方案都是需要截取229根原材料。这个研究型案例的解决过程，提示我们利用线性规划解决实际问题时，约束条件依实际背景考虑应更全面，这样既达到了优化的目的，同时也减少了计算量。这一点提升了课堂教学中理论应用的灵活性。

4 结 语

军事运筹学课程不单是理论与方法的学习过程，更是一个应用过程，是一个主动建构的过程。一切知识、技能和思想都是活的，必须经过学习者主体感知、消化、改造，使之适应自己的认知结构，才能理解和掌握。研究型案例教学，通过问题的研究、建模、求解的过程，为学员建立了一个很好的“发散思维、激发创新”的平台。通过讨论、研究，积极寻找解决问题的思路和工具，创造性地用到相关课程的知识和方法，提高了学员综合运用交叉课程知识解决实际问题的能力。这个研究型案例中，学员就很好地运用了计算机课程中二叉树的知识和选修课中matlab数学软件的工具，达到了提升课堂教学宽度的目的。但使用此工具的学员比例还很少，充分说明了加强研究型案例教学和开设matlab数学软件课程的必要性。研究型教学“课内理论—课外研究”的模式，增强了学员的优化意识，锻炼了综合其他课程、利用数学软件解决实际问题的能力，实现了军事运筹学课程从理论到实践的飞跃。

[1] 张安富．改革教学方法——探索研究型教学[J]．中国大学教学，2012(1)：65-67.

[2] 王晓，刘雄伟．《微分方程》课程研究型教学的探索与实践[J]．高等教育研究学报，2013(2)：27-30.

[3] 苏永美．第一型线面积分的研究型教学方案探析[J]．大学数学，2015(6)：110-115．

[4] 毛琪莉．理工科专业高等数学研究型教学的探讨[J]．湖北理工学院学报，2013(6)：67-70.

[5] 钱颂迪．运筹学[M]．4版.北京：清华大学出版社，2013：16-17.

[6] 郭永发．数学教育理论的实践[M]．北京：中国林业出版社，2004：228-229.

(编辑：凌春霞)

Exploration and Practice of Research-oriented Teaching in Military Operations Research

CHEN Shuzhen, ZHONG Min, CHEN Bowen

(General Courses Department, Military Transportation University, Tianjin 300161, China)

The paper explores concrete teaching method of “theory in class and research out of class” by applying research-oriented teaching mode in military operations research. In order to cultivate students’ scientific research capacity and arouse their aspiration and interest of learning, it analyzes the design principle, operation process and announcements of research-oriented teaching mode from teaching application, optimal implementation and conclusion research of a specific application example of linear programming theory.

research-oriented teaching; linear programming; model solving

2016-10-14；

2016-12-29．

陈淑珍(1966—)，女，硕士，副教授.

10.16807/j.cnki.12-1372/e.2017.04.016

E251

A

1674-2192(2017)04- 0066- 05