小型风机叶片结构损伤识别实验模拟研究

张 为，韩延琴，张 鑫

(1.甘肃东兴铝业有限公司陇西分公司，甘肃 陇西 748199； 2.兰州铁路局兰州电务段，兰州 730000)

小型风机叶片结构损伤识别实验模拟研究

张 为1，韩延琴1，张 鑫2

(1.甘肃东兴铝业有限公司陇西分公司，甘肃 陇西 748199； 2.兰州铁路局兰州电务段，兰州 730000)

风机叶片由于受到复杂荷载和各种突然因素的作用而极易发生结构损伤;针对传统无损检测技术效率较低、需要先验知识、精度不高的缺点，文中采用基于振动特性的结构损伤识别方法辨识并比较研究叶片损伤前后结构参数的变化，同时对损伤进行定位;首先搭建小型风机叶片振动检测实验平台，采集叶片损伤前后的振动响应数据；其次利用自互功率谱法辨别叶片损伤前后的模态参数，通过实验数据对比其损伤前后固有频率的变化；最后利用轴向振型差法对叶片损伤进行定位;实验结果表明，在实验室条件下，基于振动的特性的结构损伤识别方法能准确辨别叶片损伤前后结构特性的变化，风机叶片各阶固有频率的下降能够作为判断其发生损伤的依据，轴向振型差法能准确实现损伤的定位。

风机叶片；振动检测；自互功率谱法；损伤识别

0 引言

风机叶片是风力发电系统能量转化的关键部分，在长期的服役过程中，由于材料老化、疲劳、腐蚀以及长期在恶劣环境下运行，极易造成叶片的损伤累积及抗力衰减等问题，风机叶片一旦损毁将造成巨大的经济损失甚至是人员伤亡。因此，针对风机叶片进行结构损伤检测，能够准确地判断损伤的发生、位置和程度，对于风机的安全运行具有重要的现实意义[1-2]。

目前研究中经常能采用的基于动力测试的全局损伤检测法主要是通过检测整体结构损伤前后的模态参数等结构动力特性的变化，来判断结构是否存在损伤以及损伤的程度[3-4]。风机叶片结构发生损伤后，其频率、振型等模态参数也会随着出现改变，基于风机叶片结构振动特性的损伤识别方法就是通过风机叶片结构的振动响应信息分析其动力特性的变化，实现其损伤的判断与定位[5-6]。本文通过在实验室条件下检测风机叶片振动特征的变化来识别叶片结构损伤，通过数据对比研究叶片出现裂纹损伤前后固有频率等振动特性的变化，并通过轴向振型差实现损伤的定位。

1 自互功率谱法

自互谱密度法是运行模态分析中的一种简单、方便的识别结构在环境激励下的模态参数的方法，是由峰值法改进和发展而来[7]。求解思想是：结构的自身振动频率将出现在其频响函数曲线的峰值处，同时可以成为上述自振频率的良好估计。对于由外界环境激励而产生的结构振动，其激励本身是未知的，因而并不能计算出它的结构频响函数，仅可以通过振动在其参考点与响应点间的自互功率谱的幅值、相位、相干函数以及传递率等来识别结构的模态参数。

由激励xi(ω)和响应fk(ω)的关系可得频响函数为：

在仅有响应输出时，可以将结构上的某点作为参考点，将其响应看作输入，根据响应点与参考点间所具备的线性相关性，建立它们的传递函数，根据求取的传递函数进行系统识别。取结构上一点为固定点，则其传递率为：

(1)

由风作用引起的地脉动或者由自然界引起的脉动激励，均可看作为平质谱，则满足：

fk(ω)=f(ω)=C1

对于结构的频率点ωi，序列gi(ω)即为该频率对应的工作模态，结构上任一位置的动态位移响应xi(ω)都能用k点的激励力fk(ω)以及系统对应的传递函数hik(ω)来表示：

(2)

其中:C1是常数。

将式(2)代入式(1)得到：

(3)

其中:C2是常数。

由式(3)可知，直接读取在wr处曲线gi(ω)的幅值及相位，就能够得到结构在对应频率下的工作振型，可将它近似看作结构在第r阶的振型。

采用自互谱密度法对结构模态参数进行识别的基本步骤如图1所示。

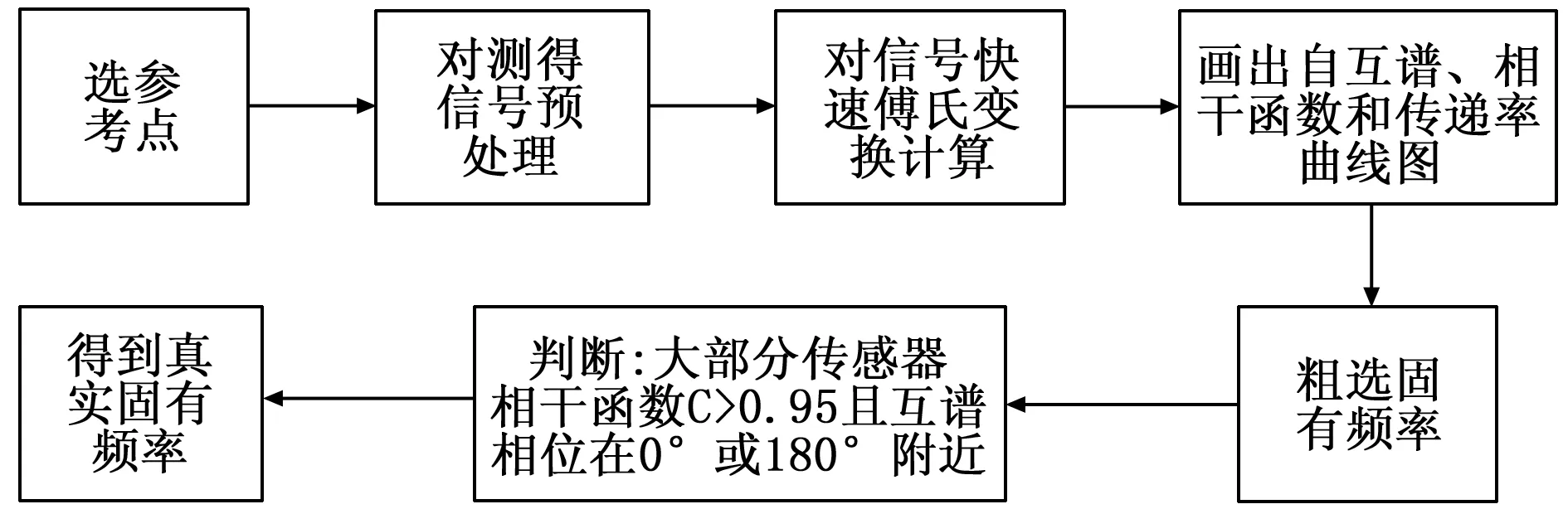
图1 自互功率谱法步骤框图

2 风机叶片振动检测实验

本次实验的主要设备有传感器、激励锤、振动数据采集系统、玻璃钢材料的小型风机叶片(长1.5 m)、微型计算机等。布置实验装置时，利用夹具把小型叶片的尾部固定，通过专用耦合剂将4个9818型压电加速度传感器依次粘在叶片表面，传感器连接线另一端与DH5937振动数据采集系统连接，每一个传感器对应振动测试仪的一个通道，计算机与DH5937振动数据采集系统相连用以储存和处理所采集的各种信号数据。叶片振动检测系统组成如图2所示。

图2 风机叶片振动检测系统组成

实验时采用单点激励、多点拾振的方式来获取同一激励下各测点的振动响应[8]。通过力锤激励的方式使小型叶片结构产生振动，由传感器来采集叶片结构动态响应信息。传感器用来检测待测信号，并对待测信号进行处理，将其转换为能够被后面仪器读取的电信号，实验中采用的传感器为9818型压电加速度传感器，其测量范围为0.2～10 kHz。

叶片的振动形式主要为挥舞和摆振[9]。因此，将4个加速度传感器等距分布在叶片的表面，间距为20 cm，用于测量叶片在挥舞和摆振两个方向的振动响应情况如图3所示，用首位编号1和2来分别表示挥舞和摆振方向的模态测点分布情况。

图3 叶片模态测点分布示意图

将加速度传感器采集到的信号传递给信号调理电路，由信号调理电路对加速度信号进行平移、放大等处理后转换为标准信号。本文选用高性能采集系统DH5937数据采集仪来读取叶片的振动响应数据。采用自互功率谱法识别结构参数时参考点的选取尤为重要，应当选取测试到的各阶频率响应比较大的传感器作为参考点[10]，本文选取四号传感器作为参考点。实验时通过力锤给叶片施加激励使其发生自由振动，通过DH5937数据采集系统采集到叶片振动信号数据，交给计算机上的专业软件DHDAS进行存储、分析及显示，然后经过图1所示的自互功率谱法各步骤求取风机叶片的自振频率和模态振型等结构模态参数。

3 风机叶片振动模态参数的辨识

3.1 完好叶片的结构模态参数辨识

通过DH5937数据采集系统采集叶片在瞬时激励下4个通道的振动时域信号如图4所示，采样时设置的采样频率为500 Hz，分析频率为195.31 Hz，分析点数为512。

图4 叶片在瞬态激励下的振动响应时域信号

对所采集到时域信号进行加窗、平均、重叠等预处理，以抑制噪声信号的随机干扰；预处理后通过FFT变换将信号转化到频域下，再通过自互功率谱法识别叶片结构的模态参数。如图5所示是各个加速度传感器的自功率谱叠加图，图6为以第四通道为参考点，其他通道与第四通道之间的叶片在挥舞方向上的互功率谱叠加图。

图5 4个通道的自功率谱图

图6 各通道与第四通道间的互功率谱幅值叠加图

由于互功率谱相比自功率谱而言，对毛刺等噪声有一定的抑制作用[11]，因此，一般选用互功率谱幅值图来对结构的自振频率进行辨识，从图6中可以粗略得到各峰值对应的频率分别为3.905 Hz、23.46 Hz、62.5 Hz、119.2 Hz和179.7 Hz。

为获得叶片结构的真实频率，需要根据互功率谱所对应的相位与相干函数对粗选频率进行判断，从而剔除毛刺等虚假模态。在频响函数理论中，如果结构幅频响应图峰值频率处的互功率谱相位在0°或者±180°左右(上下波动±30°)，同时在该峰值频率处的相干函数值能够达到0.95以上，则该峰值频率即为结构的真实固有频率[12]。互功率谱对应的相位与相干函数如图7所示。从图7可以看出叶片互功率谱幅值图中5个峰值频率所对应的互谱相位分别是180°，180°，180°，0°和-180°，且每个峰值频率所对应的相干函数均大于0.95，这说明各个峰值频率就是风机叶片的各阶固有频率。用同样的方法可辨识完好叶片在挥舞方向和摆振方向的各阶固有频率，如表1和表2所示。

图7 互功率谱对应的相位与相干函数图

表1 叶片挥舞方向的频率检测结果 Hz

表2 叶片摆振方向的频率检测结果 Hz

由模态分析法可知，通过传递率在结构固有频率位置处的幅值可以得到振型的大小，该频率处振型的方向可由互功率谱在对应频率位置的相位或传递率实部所对应的符号来确定。在实际操作时，先归一化处理各个传感器所对应的振型幅值，然后通过曲线拟合的方法便可获得小型叶片整体结构的振型拟合曲线。一般来说，分析叶片振动时只需前两阶振型即可，图8和图9为小型叶片在无损状态下挥舞方向上的第一、二阶振型曲线拟合图。

图8 无损叶片一阶挥舞方向振型拟合曲线 图9 无损叶片二阶挥舞方向振型拟合曲线

3.2 损伤叶片的结构模态参数辨识

根据叶片在实际运行中的裂纹损伤特点，本文实验采用在叶片距离叶根40%l(l为叶片长度)的位置处通过开裂纹的方式模拟结构损伤，以不同的裂纹深度来模拟叶片的不同损伤程度[13]。损伤模拟以叶片裂纹的存在对其质量分布没有影响为前提进行。叶片横向裂纹损伤位置如图10所示。

图10 叶片横向裂纹损伤位置示意图

实验中模拟小型风机叶片分别出现了损伤程度(h/D,D为叶片宽度,h为裂纹长度)为10.0%、15.0%的损伤。进行含损伤叶片的振动检测实验，对损伤叶片进行模态分析，得到叶片损伤后的动态特性参数如表3和表4所示。

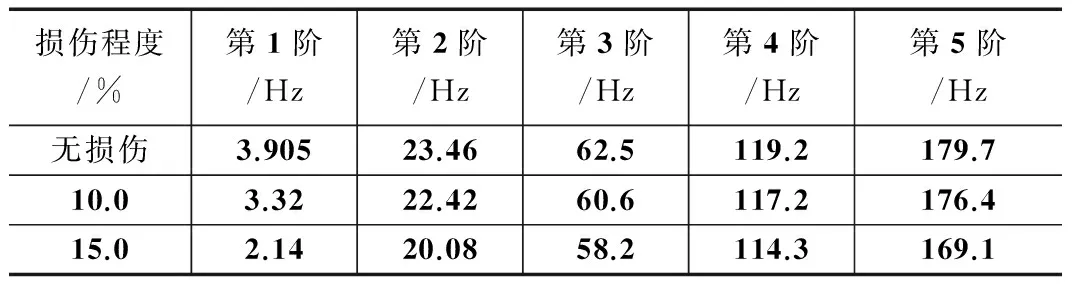
表3 损伤后叶片挥舞方向的频率检测结果

表4 损伤后叶片摆振方向的频率检测结果

从表3和表4的叶片挥舞方向和摆阵方向的固有频率检测结果可以看出，当小型风力机叶片受到损伤时，随着损伤程度的增加，叶片在挥舞方向和摆阵方向的各阶固有频率均会降低，并且高阶频率的下降更加明显。风机叶片结构损伤会导致各阶固有频率下降，各阶固有频率的下降能够作为判断风机叶片是否发生损伤的依据指标。

4 风机叶片结构损伤定位

本文通过轴向振型差变化率[14-15]对叶片结构进行损伤诊断的方法主要是因为叶片具有轴向空间结构，所谓轴向空间结构是指其轴向尺寸远远超过其他方向。结构破损导致其局部刚度的改变以及模态振型在结构局部区域的变化。当在结构的某单元处出现损伤时，其轴向振型差变化率值在损伤位置处会发生大的变化，而其他未损伤单元变化不明显。假设结构在无损伤情况下的振型为Φij，i为振型的阶次，j即振型的节点号，*表示损伤振型，则第i阶轴向振型差变化率ηij定义为:

(4)

其中:j≥2。

根据上述计算得到的损伤前后小型叶片的固有频率和振型，采用式(4)计算轴向振型差变化率对小型叶片的损伤进行定位，结果如图11所示。由图11可以看出，裂纹所在位置与曲线峰值是相对应的，即裂纹所在位置为峰值点处所代表的传感器的区域附近。与图10中模拟的叶片横向裂纹的位置相符，从而证明了采用轴向振型差变化率法对叶片损伤进行定位的可行性。

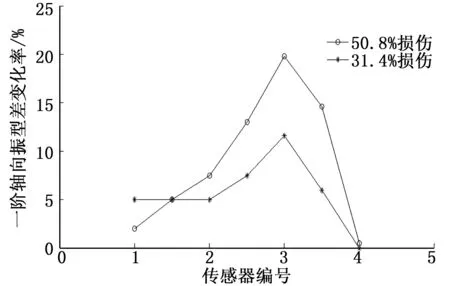
图11 两种损伤程度的一阶轴向振型差变化率曲线截图

5 结论

本文在实验室条件下搭建了小型风机叶片振动检测实验平台，利用自互功率谱法辨识了叶片在损伤前后的频率、振型等振动特性，通过对比研究发现风机叶片结构损伤会导致各阶固有频率下降，各阶固有频率的下降能够作为判断风机叶片是否发生损伤的依据指标；同时利用轴向振型差法实现了叶片损伤的定位，裂纹所在位置与曲线峰值点处相吻合，也就是裂纹所在位置为峰值点所代表的传感器的区域附近。

[1] 陶 金,张 雪,刘煜龙,等.我国风力发电的现状和前景探讨[J].现代机械,2013(3):26-28.

[2] 徐金龙.风机叶片疲劳损伤的DPP-BOTDA监测与评价方法研究[D].哈尔滨:哈尔滨工业大学,2013.

[3] 李芒芒,李录平,晋风华.模态应变能理论及其在风力机叶片损伤识别中的应用[J].可再生能源,2012,30(3):27-31.

[4] 韩红飞.基于振动模态参数和神经网络的管道裂纹损伤识别研究[D].上海:华东理工大学,2013:18-61.

[5] 乔印虎.风力发电机叶片振动研究与保护[D].乌鲁木齐:新疆大学,2006:1-8.

[6] 李芒芒.风力机叶片机械损伤动态监测方法与技术研究[D].长沙:长沙理工大学, 2012.

[7] 姜大正,洪 明.运行模态分析技术在船舶结构振动中的应用[J].中国船舰研究,2010,6(5):22-26.

[8] 孙 杰.基于多模态参数的桥梁结构损伤识别方法研究[D].武汉:武汉理工大学,2013.

[9] 李成良,王继辉,薛忠民,等.基于ANSYS的大型风机叶片建模研究[J].玻璃钢/复合材料,2009(2):52-55.

[10] 王 峥.大型风机叶片结构损伤诊断方法研究[D].兰州:兰州交通大学,2015.

[11] 孙鑫晖.频域模态参数识别研究及其软件实现[D].南京:南京航空航天大学,2010.

[12] 康剑飞.车桥动态特性的试验模态分析及数值模拟分析方法研究[D].西安:长安大学,2006,7-15.

[13] 李录平,李芒芒,晋风华,等.振动检测技术在风力机叶片裂纹故障监测中的应用[J].热能动力工程,2013(2):207-212.

[14] 方治华,岳鹏飞,张微娜.基于轴向振型变化率的空间刚架结构损伤研究[J].桂林理工大学学报,2013,33(1):56-61.

[15] 顾桂梅,王 峥,汪芳莉.基于轴向振型差变化率的风轮叶片结构损伤识别方法研究[J].玻璃钢/复合材料,2014(11):12-16.

SimulationResearchforDamageIdentificationofSmall-scaleWindTurbineBlade

ZhangWei1，HanYanqin1，ZhangXin2

(1.GansuDongxingAluminumIndustryCo.Ltd,Longxi748199,China;2.LanzhouRailwayBureau,Lanzhou730000,China)

Wind turbine blade is prone to be damaged because of suffered alternating load and other kinds of factors. Aiming at the shortcomings of the traditional nondestructive identification technology, a damage identification method is used to identify structural parameters of blade and compare the change before and after damaged. The localization of the structural damage of wind turbine blade is realized at the same time. Firstly, the wind turbine blade vibration identification experimental platform set up, the blade vibration response data is collected. Then the self-cross spectrum density method is used to identify model parameters of wind turbine blade before and after damaged. The change of natural frequency of the blade before and after damaged is compared by the experimental data. Finally axial mode difference method is used to fix a position on the blade damage. Experimental results show that the damage identification method can accurately identify the structural characteristics of the leaves before and after damaged. The decrease of the natural frequency of the wind turbine blade can be used as a basis for judging the occurrence of the damage, and axial mode difference method can accurately realize the location of damage.

wind turbine blade; vibration detection; self-cross spectrum density method; damage identification

2016-10-23；

2016-11-18。

张 为(1987-),男，甘肃定西人,大学,助理工程师，主要从事机械故障诊断方向的研究。

1671-4598(2017)04-0240-04DOI：10.16526/j.cnki.11-4762/tp

TK

A