镀层表面轮廓曲线分形维数计算方法的评价

吴成宝*，田巨，刘传生，陈峥华，王舰，龚煜，李璐瑶

（1.广州民航职业技术学院飞机维修工程学院，广东 广州 510430；2.华南理工大学机械与汽车工程学院，广东 广州 510640；3.广州白云国际机场地勤服务有限公司机务工程部，广东 广州 510470）

镀层表面轮廓曲线分形维数计算方法的评价

吴成宝1,2,*，田巨1，刘传生1，陈峥华3，王舰1，龚煜1，李璐瑶1

（1.广州民航职业技术学院飞机维修工程学院，广东 广州 510430；2.华南理工大学机械与汽车工程学院，广东 广州 510640；3.广州白云国际机场地勤服务有限公司机务工程部，广东 广州 510470）

镀层表面轮廓曲线具有分形结构，可以用分形维数(D)来定量表征。为了验证现有D值测算方法的准确性，利用W–M分形函数生成了具有不同D值的标准表面轮廓曲线，并用垂直截面法、尺码法、盒维数法、方差法、结构函数法、协方差加权法、功率谱法、均方根法共8种方法计算了其D值。研究表明，尺码法的相对误差范围在6.20% ～ 22.77%之间，平均相对误差最大，为16.76%；其次是协方差加权法，其相对误差范围为2.17% ～ 21.35%，平均相对误差为11.73%；盒维法、功率谱法和方差法的平均相对误差分别为8.61%、6.92%和5.25%；均方根法和垂直截面法的相对误差范围分别为0.51% ～ 9.84%和0.19% ～ 3.97%；结构函数法的最大相对误差仅为1.21%，最小相对误差低至0.01%，平均相对误差仅为0.45%。因此，结构函数法最准确，是计算分形维数的最佳方法。

镀层；表面轮廓曲线；分形函数；分形维数；计算

镀层的表面形貌和粗糙度对镀层的耐磨性、减摩性，被加工零件的精度以及光学、热学等性能有影响[1-4]，因此，如何准确地表征镀层的表面形貌受到广泛关注。在传统分析中，镀层表面被看作是对某一平均平面的偏差，且与描述其他粗糙平面一样，通常用统计学参数和粗糙度指数进行量化描述[1]，并以此来考察镀层的表面形貌特征与其咬合力、附着力、耐磨性、硬度等性能的相关性，以及对工件光学特性、传热特性、抗化学腐蚀等性能的影响。但是，对表面细节特征研究发现：在扫描电镜下，如果这种表面轮廓被不同的倍数重复放大时，更加精细的结构不断出现，而且轮廓在不同放大倍数下都是不光滑的，在任何点都不存在切线，所以轮廓函数是处处不可微的。另外，当轮廓被放大时，放大后的表面和原始表面的概率分布非常相似[5-6]。然而，上述参数只能描述表面形貌沿表面单一方向的统计特征，并不能准确地反映这种自相似性的特征。

早在1978年，Sayles等[7]认为，表面形貌是一种非稳定的随机过程，传统的统计学参数不能全面表征断面形貌的随机行为和细节特征。随着分形几何学的诞生，1984年Mandelbrot[8]首次提出用分形维数定量描述表面形貌特征。从此以后，分形理论已广泛应用于包括电镀表面在内的表面形貌特征的定量表征[9-11]。目前，表面轮廓分形维数计算的常用方法主要有8种[12-15]：垂直截面法、尺码法、盒维数法、方差法、结构函数法、协方差加权法、功率谱法和均方根法。尽管这些方法的原理都基于相同的分形理论模型，但其测算方法都不尽相同，进而使得各方法的稳定性和偏差均存在差异。在应用这些方法计算具体的表面轮廓分形维数时，研究工作者往往无法快速地选择一种最合适的计算方法。为使计算所得轮廓分形维数能准确地表达出表面轮廓的真实不规则行为，本文在标准轮廓曲线的基础上，对比分析了以上8种计算方法的准确性，为镀层表面轮廓分形维数的计算优选方法。

1 表面轮廓曲线分形维数的测算方法

1. 1 垂直截面法

轮廓曲线的长度L在一定的尺度范围内与测量标尺r之间具有如下关系[15-17]：

式中，L0为断面轮廓起始图形的边长，是具有长度量纲的常数；DL为轮廓曲线分形维数，对同一个断面而言为常数。

式(1)可改写为：

1. 2 尺码法

用某个选定尺码以分规方式沿着轮廓曲线测量，保持尺码分规两端的落点始终在轮廓曲线上，如此测量全部曲线后，所得曲线长度就是选定尺码与分规度量步数之积。选择n个尺码ri(i= 1, 2, ···,n)测量轮廓曲线，每个尺码测得的曲线长度为li，ri和li均具有长度量纲。由此得到一组数据：[r1,l1]，[r2,l2]，···，[rn,ln]。在双对数坐标中以最小二乘法原理对尺码和曲线长度两参数进行线性回归，根据回归直线的斜率α就可以按式(3)得到轮廓曲线分形维数估计值[12-13,18]。

1. 3 盒维数法

用一个边长等于1(长度量纲)的方盒子将轮廓曲线覆盖，将此方盒分割成含有2n个小方盒的网格集，小方盒的边长为2n−，用这个网格集覆盖轮廓曲线，统计出与轮廓相交的小盒子数量(M)n，则曲线的分形维数[12, 19-20]：

1. 4 方差法

该求算方法[12,21]是尺码法的一种变异方法，以宽为r的矩形框首尾相接地将轮廓曲线覆盖起来，令第i个框内轮廓的最大值与最小值之差为Hi，若尺度r很小，则Hi的值就逼近曲线的长度。因此，等价的测度数V(r)的表达式为：

式中，r和Hi具有长度量纲。在双对数坐标中对V(r)与r作线性回归分析，由直线斜率α可以得到轮廓曲线的分形维数：

1. 5 结构函数法

将轮廓曲线视为一个时间序列Z(x)，则具有分形特征的时间序列能使其采样数据的结构函数S(t)满足[12, 14, 22-24]：

在本研究中，式(7)中的t代表数据点的间隔个数，任意选择，无量纲；S(t)是t的函数，无量纲；x为轮廓曲线上的横坐标；Z(x)为坐标x上所对应的轮廓高度，为长度量纲；[Z(x+t)−Z(x)]2表示差方的算术平均值；c为常数，无量纲。

针对若干个t对轮廓曲线的离散信号计算出相应的S(t)，然后在对数坐标中得到lgS(t)−lgt直线的斜率α，则DL与斜率α的转换关系为：

1. 6 协方差加权法

具有分形性质的时间序列Z(T)满足以下标度关系：

在本研究工作中，Z(T)为轮廓曲线的函数，T为坐标间隔，T0为起始坐标，ζ为常数.

设T0= 0，Z(T)= 00，则时间序列的方差或协方差[12]为：

式(11)表达了时间序列的协方差与时间区间的标度律，它表明时域T内的协方差与时域尺度T呈幂指数关系，而这个幂指数与分形维数有关。对于一条数字化的轮廓曲线，将其视为时间序列，用n个时域iT(i= 1, 2, ···,n)来计算它的协方差σ(T)，在对数坐标中回归出lg[σ(T)]−lgT直线，于是回归直线的斜率α与DL的转换关系如式(6)所示。

1. 7 功率谱法

若以功率谱S(ϖ)为测度，以频率ϖ为尺度，则有[14,25-26]：

拟合lgS(ϖ)−lgϖ数据点，设直线斜率为α，则分形曲线的分形维数为：

1. 8 均方根法

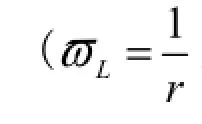
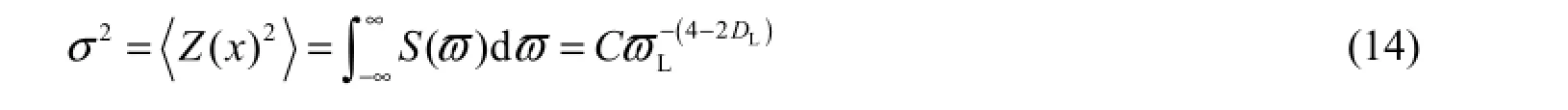
式中C为常数，亦即：

所拟合的lgσ−lgL直线的斜率α与DL的关系如式(6)所示。

2 标准轮廓曲线的生成

W–M分形函数是由1875年发现的连续但处处不可微的函数演变而成。1980年，M. V. Berry详细讨论了W–M分形函数的数学性质，奠定了W–M分形函数广泛传播和适用的基础。随后，Mandelbrot和Peitgen等人提出了轮廓曲线具有统计自相似分形特征，可用W–M分形函数来刻画表征。1990年，为了适合工程表面的应用，M. Majumdar和B. Bhushan提出了对原W–M分形函数的修正形式，简称M–B模型。其表达式如下：

由式(16)可知，W–M函数主要由D、G、λ、n所确定，同时要避开λ= 0的点。另经大量计算发现，n不可能取无穷大，也不需要取过大值，实际应用中一般取10 ～ 100之间的值。x在[0.5, 0.8]区间取值。

在Matlab中，D为1.1时的模拟程序如下(其他情况只需将程序中的D值改成相应的分形维数值)：

D为1.1、1.3、1.5、1.7、1.9时W–M分形函数的模拟图如图1所示。

图1 不同D值的W–M分形曲线Figure1 W–M fractal curves having differentDvalues

由图1可明显地看出曲线的复杂程度随D值的增大而不断增加。D值越大，轮廓结构越复杂，轮廓细节越丰富。

3 结果及分析

为对比垂直截面法、尺码法、盒维法、方差法、结构函数法、协方差加权法、功率谱法和均方根法的准确性，用上述方法计算了理论D值分别为1.1、1.3、1.5、1.7及1.9的W-M分形曲线的D值，结果见表1。

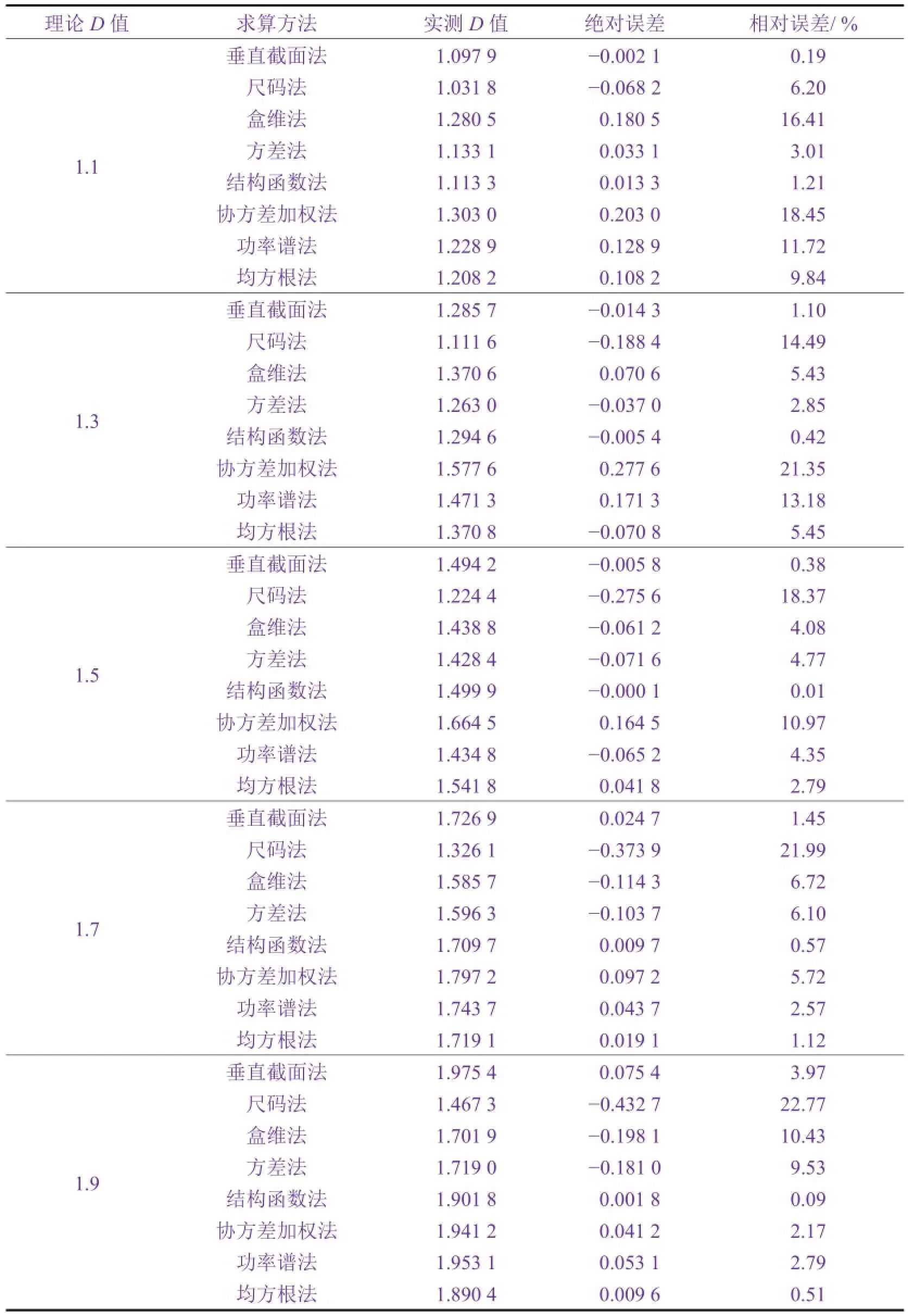
表1 不同方法求算的W–M分形曲线的D值Table1 Dvalues of the W–M fractal curves calculated by different methods

比较表1中的求算结果可以看出，尺码法求算的D值相对误差范围在6.20% ～ 22.77%之间，平均相对误差最大，高达16.76%；其次是协方差加权法求算的D值的相对误差，范围为2.17% ～ 21.35%，平均相对误差为11.73%；盒维法、功率谱法和方差法求算的D值的相对误差范围依次为4.08% ～ 16.41%、1.05% ～ 13.18%、0.73% ～ 9.53%，平均相对误差分别为8.61%、6.92%和5.25%；均方根法、垂直截面法和结构函数法求算的D值相对误差都比较小(分别为0.51% ～ 9.84%、0.19% ～ 3.97%和0.01% ～ 1.21%)，其中结构函数法求算的D值的平均相对误差仅为0.45%。由此可知，用结构函数法求算D值可以保证相当理想的计算精度。

4 结论

利用现有8种常用的表面轮廓曲线分形函数计算方法计算了具有一定分形维数的W–M分形函数的模拟曲线的分形维数。研究发现，尺码法的平均相对误差最大，其次是协方差加权法，再次为盒维法、功率谱法和方差法，均方根法和垂直截面法的相对误差比较小，而结构函数法的相对误差最小，准确度最高。

[1] 孔磊, 胡会利, 于元春, 等. 工艺参数对三价铬镀铬层粗糙度的影响[J]. 电镀与环保, 2013, 33 (1): 17-20.

[2] 朱亚哲, 李保成, 李慧. 脉冲参数对Q235钢上镍镀层表面形貌和显微硬度的影响[J]. 电镀与涂饰, 2011, 30 (12): 13-16.

[3] 李远会, 张晓燕, 李广宇, 等. 电沉积铜–钨复合镀层的表面形貌和性能研究[J]. 电镀与涂饰, 2010, 29 (5): 6-8.

[4] CUBILLOS G I, ROMERO E, ALFONSO J E. Influence of corrosion on the morphology and structure of ZrOxNy–ZrN coatings deposited on stainless steel [J]. Materials Chemistry and Physics, 2016, 176: 167-178.

[5] 许志倩, 闫相祯, 杨秀娟, 等. 粗糙表面几何形貌特征的分形参数描述[J]. 润滑与密封, 2015, 40 (9): 1-9.

[6] ZHANG X H, XU Y, JACKSON R L. An analysis of generated fractal and measured rough surfaces in regards to their multi-scale structure and fractal dimension [J]. Tribology International, 2017, 105: 94-101.

[7] SAYLES R S, THOMAS T R. Surface topography as a nonstationary random process [J]. Nature, 1978, 271 (5644): 431-434.

[8] MANDELBROT B B, PASSOJA D E, PAULLAY A J. Fractal character of fracture surfaces of metals [J]. Nature, 1984, 308 (5961): 721-722.

[9] 汪笑鹤, 徐滨士, 胡振峰, 等.n-Al2O3/Ni–Co纳米复合电刷镀层表面形貌的分形维数研究[J]. 电镀与涂饰, 2010, 29 (11): 33-36.

[10] 徐金来, 吴成宝, 刘钧泉. 镀层表面形貌的分形维数定量表征[J]. 电镀与涂饰, 2009, 28 (5): 31-34.

[11] PIASECKI R. Detecting self-similarity in surface microstructures [J]. Surface Science, 2000, 454/455/456: 1058-1062.

[12] ZHONG L, ZENG F, XU G X. Comparison of fractal dimension calculation methods for channel bed profiles [J]. Procedia Engineering, 2012, 28: 252-257.

[13] FENG Z G, SUN X Q. Box-counting dimensions of fractal interpolation surfaces derived from fractal interpolation functions [J]. Journal of Mathematical Analysis and Applications, 2014, 412 (1): 416-425.

[14] YUAN C Q, LI J, YAN X P, et al. The use of the fractal description to characterize engineering surfaces and wear particles [J]. Wear, 2003, 255 (1/2/3/4/5/6): 315-326.

[15] 丰杰, 谭云, 陶萍, 等. 内部氢对奥氏体不锈钢拉伸断口分形维数的影响[J]. 材料导报, 2014, 28 (4): 118-121, 133.

[16] 张彦华, 曾祥恒, 陈丙森. 材料断口分形维数分析[J]. 材料科学与工艺, 1995, 3 (2): 14-18.

[17] 吴成宝, 梁基照. 无机粒子填充高分子复合材料断口的分形特征及其测定方法[J]. 塑料科技, 2007, 35 (8): 60-64.

[18] Brown C A, Savary G. Describing ground surface texture using contact profilometry and fractal geometry [J]. Wear, 1991, 141 (2): 211-226.

[19] DUBUC B, QUINIOU J F, ROQUES-CARMES C, et al. Evaluating the fractal dimension of profiles [J]. Physical Review A, 1989, 39 (3): 1500-1512.

[20] GAGNEPAIN J J, ROQUES-CARMES C. Fractal approach to two-dimensional and three-dimensional surface roughness [J]. Wear, 1986, 109 (1/2/3/4): 119-126.

[21] STUPAK P R, KANG J H, DONOVAN J A. Fractal characteristics of rubber wear surfaces as a function of load and velocity [J]. Wear, 1990, 141 (1): 73-84.

[22] MAJUMDAR A, BHUSHAN B. Role of fractal geometry in roughness characterization and contact mechanics of surfaces [J]. Journal of Tribology, 1990, 112 (2): 205-216.

[23] WU J J. Characterization of fractal surface [J]. Wear, 2000, 239 (1): 36-47.

[24] GANTI S, BHUSHAN B. Generalized fractal analysis and its applications to engineering surfaces [J]. Wear, 1995, 180 (1/2): 17-34.

[25] 葛世荣, TONDER K. 粗糙表面的分形特征与分形表达研究[J]. 摩擦学学报, 1997, 17 (1): 73-80.

[26] TRICOT C, FERLAND P, BARAN G. Fractal analysis of worn surfaces [J]. Wear, 1994, 172 (2): 127-133.

[ 编辑：温靖邦 ]

Evaluation on the methods for calculating the fractal dimension of surface profile curve of coating

WU Cheng-bao*, TIAN Ju, LIU Chuan-sheng, CHEN Zheng-hua, WANG Jian, GONG Yu, LI Lu-yao

The surface profile curve of coating is fractal and can be quantitatively characterized by the fractal dimension (D). To verify the accuracy of the present methods for calculating theDvalue, the W-M fractal function was used to generate the standard surface profile curves with different fractal dimensions, and then theDvalues were calculated by eight methods including the vertical section method, yard stick method, box counting method, variation method, structure function method, weighted covariation method, power spectrum density method and root mean square method. The results indicated that the yard stick method has a maximum relative error ranging from 6.20% to 22.77% with a mean relative error of 16.76%, which is the largest among those of all the methods; the relative error of weighted covariation method is in a range between 2.17% and 21.35%, and 11.73% averagely; the mean relative errors of box dimension method, power spectrum density method, and variation method are 8.61%, 6.92% and 5.25%, respectively; the mean relative errors of mean square root method and vertical section method are 0.51%-9.84% and 0.19%-3.97%, respectively; and the structure function method has a relative error of 1.21% maximum, 0.01% minimum, and 0.45% averagely. Therefore, the structure function method has the highest accuracy and is most suitable for calculating the fractal dimension.

coating; surface profile curve; fractal function; fractal dimension; calculation

TQ153

A

1004 – 227X (2017) 08 – 0403 – 06

10.19289/j.1004-227x.2017.08.004

2017–02–14

2017–04–03

中国民用航空局2015年民航科技创新引导资金；广东省二类品牌专业建设项目；广州民航职业技术学院校级科研项目。

吴成宝（1978–），男，湖南邵阳人，博士，博士后，副教授，主要从事粉体工程材料及高分子复合材料成型加工过程中的物理与化学和民用飞机结构的研究。

作者联系方式：(E-mail) wuchengbao@126.com。

First-author’s address:School of Aircraft Maintenance Engineering, Guangzhou Civil Aviation College, Guangzhou 510430, China