大区域含水层中局部复杂水流过程的多尺度模拟
2017-05-07曾季才查元源杨金忠
曾季才,查元源,杨金忠
(武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072)
1 研究背景
长期以来,大区域地下水流运动数值模拟受到计算精度与成本的相互制约。在区域尺度问题的模拟中,往往通过尺度提升来将点尺度实测信息高度平滑地离散到大时间和空间网格上,进而与区域尺度模型进行尺度匹配[1-3],本质上放弃了对局部小尺度问题的精细刻画。而保留全区域大尺度过程描述,并将研究重点放在具有小尺度水流运动特征的局部区域,符合许多实际问题的求解需求,因此产生了一系列在区域尺度和局部尺度上实现多尺度水流运动模拟的数值模型。这些模型往往借助非均匀网格离散方法来求解地下水方程,例如基于有限单元法的地下水模型求解软件(如FEFLOW[4]和S3D[5]),它们主要采用直接局部加密方法对全区域内不同分辨率的网格节点进行统一求解,容易在小尺度模拟范围外增加大量不必要的渐变节点,同时其计算效率和精度易受非均匀网格剖分质量的显著影响,从而增大实际应用的难度。此外在溶质运移等非对称矩阵问题的求解中,这类方法的网格加密速度和加密极限受算法收敛性和跨尺度网格混叠误差的影响[6];与此同时,基于有限差分法的地下水模型求解软件(如MODFLOW-USG[7]),则因为非结构化的网格容易产生不规则的稀疏带状矩阵以及条件对角占优问题,增大了应用于大区域尺度时的矩阵求解难度;此外,基于有限差分局部网格加密的多网格耦合模型(如MODTMR[8-9]和MODFLOW LGR[10-11]),主要通过连接不同分辨率的独立网格节点来求解不同尺度的地下水流运动问题,这类模型方法在处理小尺度复杂边界条件及源汇项等问题上的灵活性及刻画精度受到有限差分网格几何形态的限制[11],目前尚不能实现大区域含水层中的多时空尺度水流过程的高效模拟[8-10],且用不同网格之间进行迭代耦合(如MODFLOW-LGR[10])来求解高度非均质含水层等存在复杂水力条件的问题时,其计算效率和精度并不能占绝对优势[12]。
本文提出一种多时空尺度耦合模型,它采用尺度分离策略,在获取区域大尺度模型粗网格解的同时,精细刻画局部小尺度水流运动过程,将不同尺度模型的时间和空间信息进行关联和传递。即在大尺度含水层构建粗网格母模型,在局部小尺度构建三维精细网格子模型,采用自由非匹配网格及自适应时间步长加密的非迭代耦合方案,进行多时空尺度的子母模型耦合,从而实现对复杂小尺度地下水流运动过程更高效和更精细的模拟。本文模型将不同尺度模型的参数输入、边界条件、初始条件和源汇项等信息进行尺度分离,通过模型边界信息传递来耦合不同时空尺度的模型。其中,大区域尺度问题求解采用有限差分单元网格地下水模型MODFLOW 2005[13],该模型对大区域地下水模拟问题有较高的稳定性和求解效率[14]并已有较大量的代码维护和改进[15-17];而局部小尺度问题求解则采用控制体积有限单元模型S3D[5],该模型能较好地适应小尺度高密度不规则网格的求解,并能适应局部大水力梯度、复杂边界条件、非均质倾斜含水层等特殊问题[5]。区别于传统多网格耦合模拟软件(如MODFLOW-LGR[10]及MODTMR[8]),本文模型为独立开发,并侧重体现小尺度模型在求解局部复杂水流运动过程时所具有的优势。在后期的研究中,该模型已衍生出饱和三维溶质运移模型[5]、拟三维饱和非饱和水流运动及溶质运移模型[18],以及三维饱和非饱和水流运动及溶质运移模型[19],对于本文模型的持续开发具有较好的延续性及扩展性。
2 三维地下水多尺度耦合模型
2.1 多尺度模型耦合框架 本文模型采用的地下水流运动控制方程及边界条件可以归纳如下:

本文模型对不同尺度的概念模型进行不同方法的数值离散,其中区域尺度模型为有限差分网格[13],而局部尺度模型则为控制体积有限单元网格[5],如图1所示。在空间上,两种空间尺度的网格可以通过各自的网格密度、分层密度和边界形状进行独立创建。对于本文区域大尺度模型而言,其继承了MODFLOW 2005软件的所有子程序包,能有效处理区域尺度地下水流的入渗、蒸发、排水、抽水等问题[13],而本文局部尺度模型S3D[5]则侧重于刻画高密度网格上具有小尺度特征的地下水流运动过程。模型为非迭代耦合,基本框架分为4部分(见图2):(1)求解区域尺度粗网格模型,并得到全局节点水头;(2)通过三维水头插值得到局部尺度模型在大时间尺度节点上的边界节点水头;(3)通过自适应时间步长调整及二阶时间插值得到任意时间节点上的小尺度模型边界水头;(4)求解小尺度模型,得到局部小尺度模型高精度解。相比MODFLOW-LGR[10]的迭代耦合方案,本文模型的非迭代耦合方案虽然损失了一定的计算精度,但由于不存在小尺度解的反馈机制,在大区域复杂水流过程及非均质问题中具有更高的计算效率[12]。
2.2 多空间尺度信息传递 在多空间尺度耦合问题中,本文模型采用三维Darcy水头插值方法来实现区域尺度模型水头信息向局部尺度模型边界节点的传递,该方法基于二维平面水头Darcy-Planar插值公式[10],主要通过地下水流运动的水头和通量本构关系——Darcy定律,来求解任意小尺度模型边界节点相对于大尺度模型节点水头所存在的水头差,从而得到其插值水头[20-21]。相比传统线性空间插值,三维Darcy水头插值方法代码实现简单,且更多地考虑了节点水力参数的空间变异性,因而更适用于有限差分模型中任意空间位置节点的水头插值。设任意小尺度模型边界节点为C,其最临近的大尺度模型节点为P0。P0在j=xyz三个轴向相邻节点之间的水流通量qpj满足达西定律:

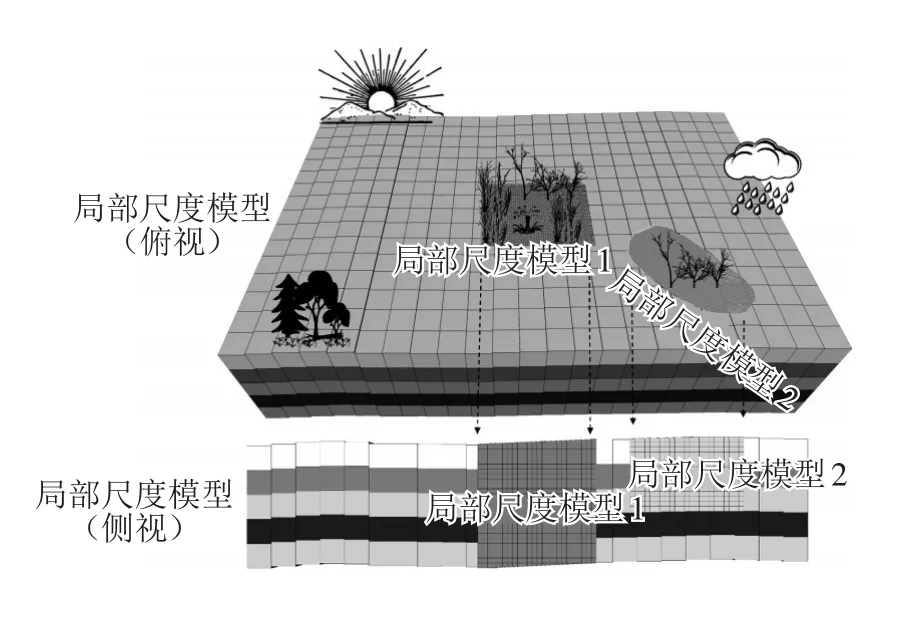
图1 多子域自由网格匹配的多尺度耦合模型示意图
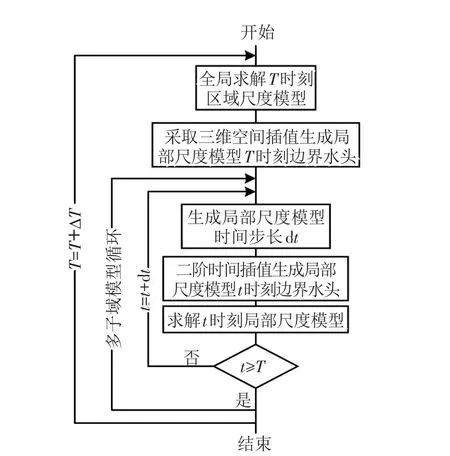
图2 本文模型流程图
式中:Cj为P0在j=x,y,z三个轴向上与相邻节点之间的导水度(定义及公式见文献[13]),m2/d;H0为大区域尺度模型节点P0的水头解,m;H0′为j轴向上与P0相邻的大区域尺度模型节点Pi(i=1,2,…,6)的水头解,m。同时,节点P0控制范围内的j方向流量qc j可以表示为:

式中:Kj为节点P0在j=x,y,z三个轴向上的水力传导度,m/d;Aj为节点P0在j=x,y,z三个轴向上的过水横截面积,m2;δlj为节点C与P0在j=x,y,z方向上的坐标差值,m;δhj为节点C与P0在j=x,y,z方向上的水头差值。
本文插值方法假设相邻母网格之间的水流通量与单个母网格内部的水流通量相等,即qpj=qcj,则由式(2)和式(3)可以得到

将j=x,y,z三个轴向上的δhj累加到P0节点的水头H0,得到节点C的插值水头hC:

2.3 多时间尺度信息传递 在多时间尺度耦合问题中,本文模型采用自适应时间步方法[22]获取小尺度模型的时间步长,用以获取自适应时间步长加密条件下的小尺度模型边界信息。该方法主要依据当前求解结果的水头变化值来调整子模型时间步长:

式中:Δt′为上一次完成求解所采纳的时间步长,d;Δhe为控制参数,用于限定某个时间步长内子模型节点所容许的水头差,m;为当前子模型解h1与上一时刻有效解h0的最大绝对差值,m;Δt为更新的时间步长,d。式可用于评估当前所使用时间步长Δt′的合理性,当ε≥ 1时认为时间步长Δt′合理,则Δt用于估算下一步时间步长;当ε<1时,认为Δt′不合理,则采纳Δt重新求解子模型。
求解子模型前,通过二阶插值方法得到任意t时刻的小尺度模型一类边界条件(图3),该二阶曲线拟合公式如下:
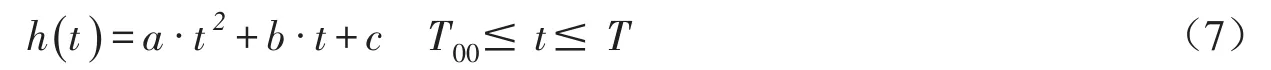
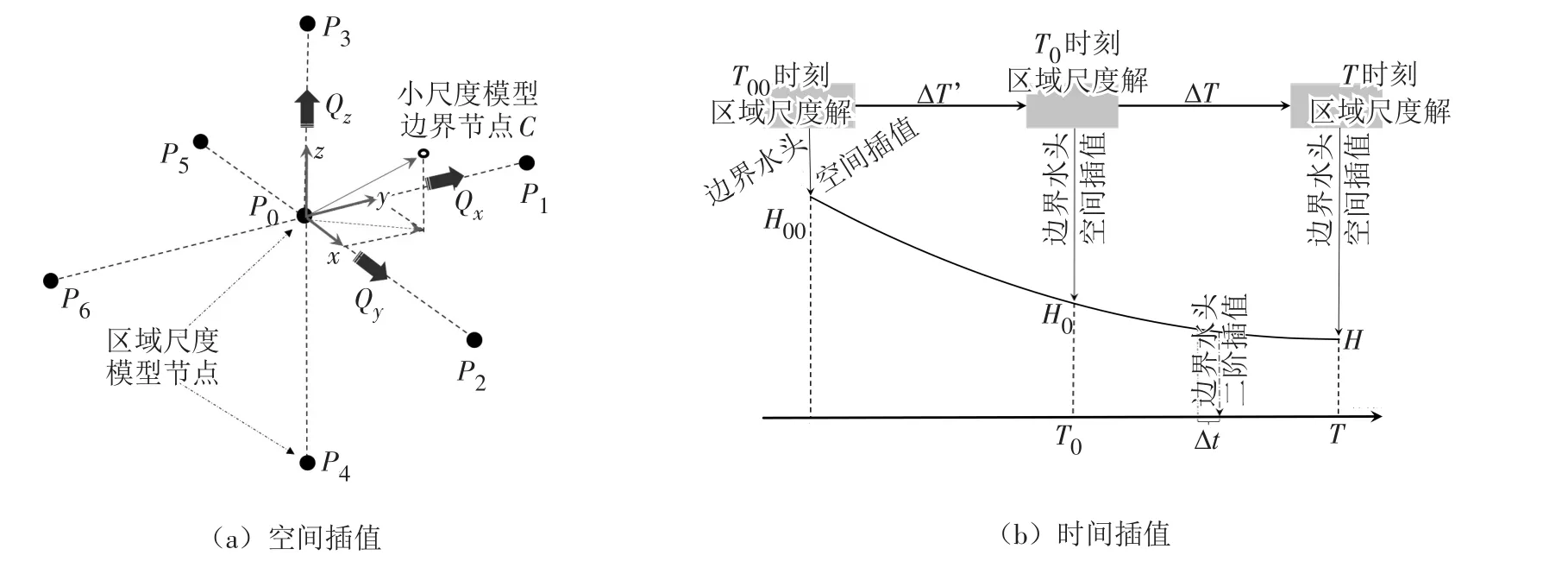
图3 基于边界水头插值的多时间和多空间尺度模型耦合
3 模型验证及分析
为验证本文模型在多空间尺度模拟、多时间尺度模拟和复杂小尺度水流运动过程模拟上具有的优势,设计了均质含水层中的2个数值验证算例,包括(1)多空间尺度大水力梯度模拟,和(2)多时空尺度复杂局部水流运动过程模拟。本文模型的验证算例建立在一个长×宽×高为1 000 m×1 000 m×50 m的均质潜水含水层内(水力传导度ks=10 m/d,给水度Sy=0.068 6,弹性释水系数μs=1.0×10-5m-1),为避免相同边界条件下不同网格密度对模型解的影响[23],将四周和底板设为隔水边界,含水层初始水头为42 m。算例在子域1内(见图4中矩形点划线方框范围)以I=300 mm/d进行持续均匀灌溉。在含水层获取了具有全区域大尺度补给系数随机场(均值为=0.167,相关长度为100 m,标准差为0.01)。
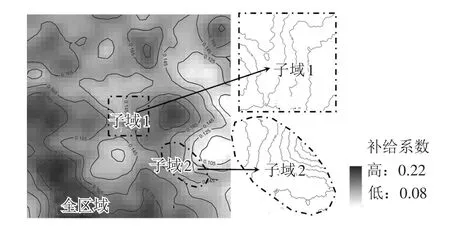
图4 多空间尺度模型参数(补给系数为例)获取示意图
3.1 多空间尺度大水力梯度模拟 本算例布设了两个分别位于(x,y)=(500 m,500 m)和(550 m,500 m),滤水段均为zbottom~ztop=20~30 m的独立抽水井,各以定流量500 m3/d和250 m3/d进行为期60 d的持续抽水。采用克里金插值方法得到如图4子域1内的复杂不规则边界形态的补给系数分区。算例将全区域划分为均匀有限差分粗网格(节点间距Δx=Δy=22.222 m),将局部尺度上的子域1采用高密度非结构化有限单元三角网(节点间距Δl≈2.5 m),等效的局部网格水平向加密比为8.9∶1,垂向加密比为1∶1。算例以通用地下水数值模拟软件MODFLOW[13]在高密度网格(节点间距Δx=Δy=2.5 m)和最小时间步长(Δt=0.1 d)下的计算结果作为高精度参照解。
图5给出了子域1在持续60 d大流量抽水条件下的末时刻水头剖面。其中,本文模型小尺度解在抽水井附近节点出现极大水头误差(0.094 m),子域1内平均水头绝对误差为0.003 9 m,其中92%的节点水头绝对误差低于0.005 m;同时,本文模型大尺度解与精细网格参照解的绝对水头误差在抽水井附近达到最大(约1.74 m)。图5中虚线代表了粗网格大尺度模型解,两个抽水井产生的漏斗降深、形状和方位均发生失真,这是由于粗网格区域尺度模型解难以用于刻画局部尺度细节,其在小尺度区域的指示精度不再作为参考。由于小尺度模型解的误差较小,可以认为这粗网格处理方式在局部大水力梯度问题中对全局大尺度解的精度影响不大。
对于大流量持续抽水问题而言,末时刻(t=60 d)误差将累积到最大值。统计显示,该时刻小尺度模型边界插值节点水头误差均值为0.001 8 m,极大值为0.008 m,且90%的插值点水头误差低于0.003 m,这些误差主要来自大尺度模型解的自身误差,并通过时间和空间的水头插值向小尺度模型节点传递并累积。小尺度模型解所获取的误差传递相比大尺度模型解在子域1范围内的巨大误差仅占比0.46%,因而可以忽略。同时从图5可以看出,子域1范围内的粗网格节点源汇项(井2)输入存在不可避免的空间错位,这种错位对子域1外的大区域尺度解影响较小,但在子域1范围内影响较大,证明了对于局部尺度问题采用小尺度模型求解的必要性。对比子域1内小尺度模型解与MODFLOW高密度时空网格下的参照解等值线图(见图6),可见本文模型在大区域尺度的局部大水力梯度问题的模拟中能实现较高精度。
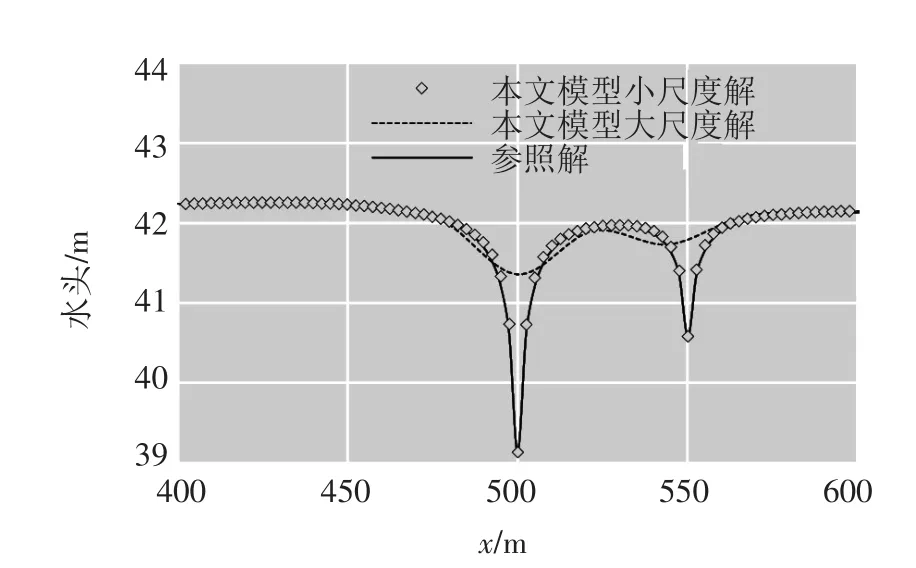
图5 对比子域1内本文模型大尺度和小尺度解与参照解(y=500 m处的x轴向剖面)
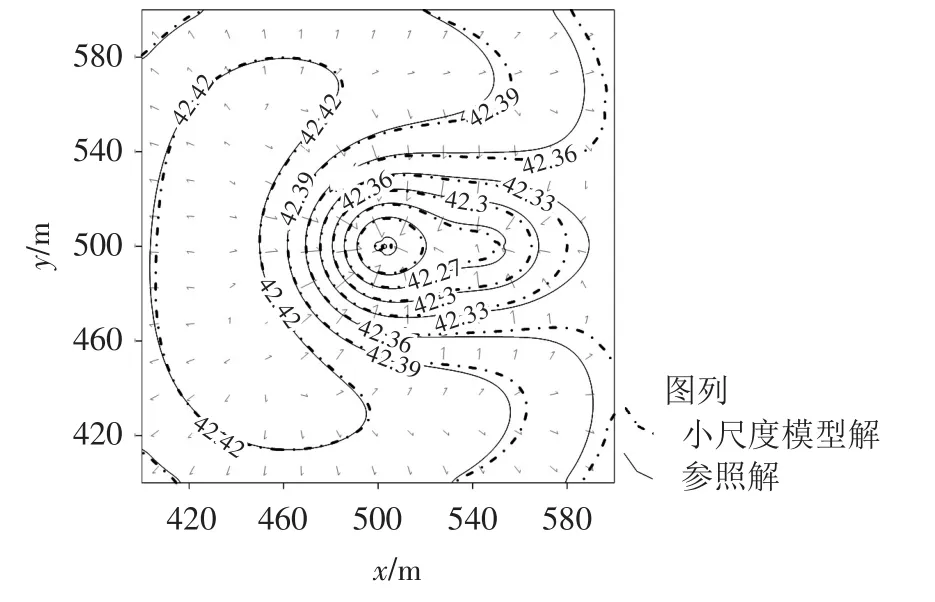
图6 对比末时刻子域1内本文模型小尺度解(虚线)与参照解(实线)
3.2 多时空尺度局部复杂水流过程模拟 在3.1节中验证算例的基础上,针对复杂时变抽水井问题,在井1处设置了如图7所示带有随机扰动(6个应力期内的抽水量均值为500、400、600、400、550和350 m3/d,标准差分别为28.9和10.7 m3/d)的抽水量时间序列,各应力期持续10 d不间断抽水;井2处抽水量设置为井1的0.5倍。其中,本文模型在局部尺度上的模拟则采用自适应时间步长,为子域1中井1和井2施加的随机扰动来表征实际抽水量的剧烈波动。此外,在子域1内,仍然以算例1中相同的入渗补给系数随机场进行相同灌溉量下的人工补给。在如图8所示的子域2内构建变密度非结构化Delaunay三角网。模型垂向模拟范围位于局部含水层(z=20~50 m高程范围内),并根据源汇项求解需要将子域2剖分为8层(见图8),该子网格无需与母网格进行严格的空间匹配,底部节点高程无需与区域尺度模型底板高程匹配。算例在子域2内设置如图8所示6个定流量(Q=-50 m3/d)抽水井(编号为3,4,…,8),滤水段高程均为zbottom~ztop=30~40 m。
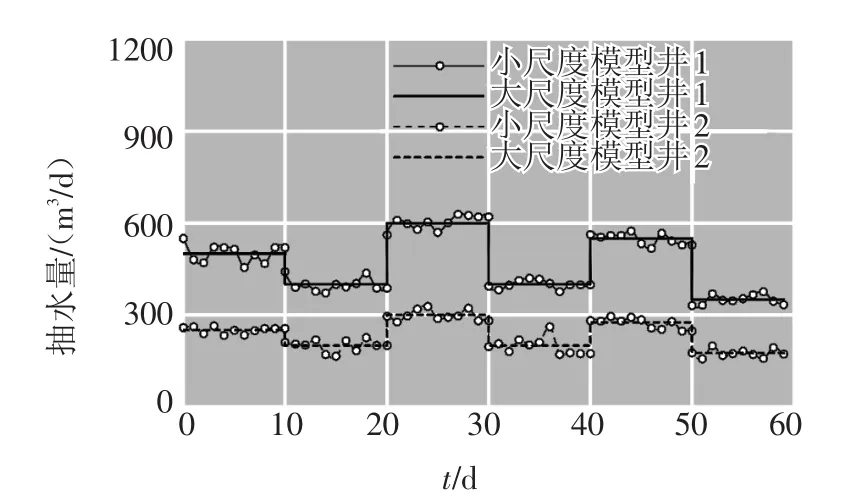
图7 子域1内井1和井2抽水流量均值和随机扰动实值时间序列
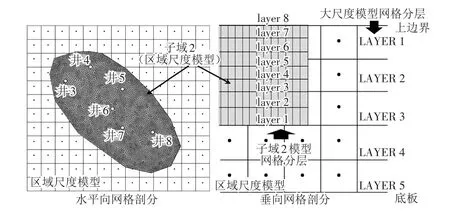
图8 子域2模型非匹配网格示意图
算例在井1和井2上施加剧烈扰动的变流量抽水井,并设置观测点A1(x=500 m,y=500 m,z=25 m)和A2(x=525 m,y=500 m,z=25 m),得到如图9(a)和(b)中观测水头随时间的变化。图9中,观测点的小尺度模型解均能较好地与参照解进行匹配,并能精细刻画局部水头变化过程;而点A1的大尺度模型解则由于施加了大时间尺度应力项而产生显著误差(图9(a)),点A2的大尺度模型解则由于稀疏网格解自身误差而与参照解之间存在大幅度偏离(图9(b))。针对本文小尺度模型在子域1内的求解精度,统计z=25 m水平剖面上所有节点的绝对水头误差随时间的变化,得到小尺度模型水头误差极大值保持在0.026 m以下(位于抽水井附近),而模拟期内所有节点平均绝对水头误差为0.005 6 m,大尺度模型“传递误差”均值为0.004 2 m,可以认为本文模型对于多时间尺度、大水力梯度问题的模拟具有较高的计算精度。统计子域1的小尺度模型边界插值节点的绝对水头误差,均低于1.0×10-4m,且均值约为2.0×10-5m,该均值约占粗网格大尺度模型“传递误差”均值的1.1%,可见本文时间和空间尺度水头插值方法能获取较高精度的小尺度模型边界水头。
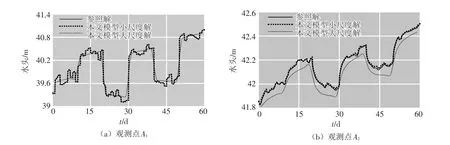
图9 对比在观测点A1和A2处的本文模型解粗网格大尺度解、高密度网格小尺度解与参照解随时间的变化
图10(a)细虚线为全区域内粗网格大尺度模型解;实线为高密度网格参照解;粗点划线为高密度网格小尺度模型解。统计得到粗网格模型解在全区域的绝对水头误差均值为0.003 1 m,可见对于存在局部时变大水力梯度的复杂流场之外的大尺度区域,本文模型粗网格解能满足大部分范围内的精度,而局部区域内(子域1和子域2)则需要采用小尺度模型进行刻画。在复杂多时空尺度、多子域、非匹配自由网格模拟条件下,图10(b)对比了本文模型在子域2中的小尺度解与参照解,其绝对水头误差均值为0.004 m,极大值为0.028 m,其中95%的子网格节点绝对水头误差低于0.01 m,对于大水力梯度条件下的区域尺度模拟而言计算精度较高。统计末时刻子域1内本文模型小尺度解的绝对误差,当单独运行子域1模型时,其均值为0.005 6 m;当同时运行子域1和2模型时,其均值为0.006 3 m。子域1内的误差出现明显增长,主要是由于子域1临近的子域2区域出现持续大水力梯度干扰,对母网格在子域1边界节点处的求解精度有微弱影响,因此在实际应用中,应尽量采用单个高密度子网格求解(覆盖)所有临近大水力梯度问题。
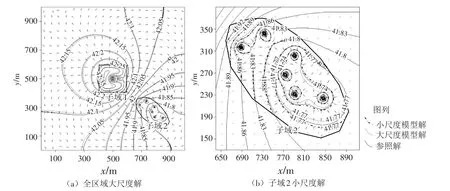
图10 对比本文模型解(等高线)与参照解

表1 本文模型计算成本及误差统计(对比参照模型)
3.3 优势与不足 本文模型继承了MODFLOW[13]作为区域尺度地下水模拟软件所具有的先天优势,将其应用于粗网格大区域尺度模型求解,能获得较高的计算效率和精度;而本文小尺度模型S3D则作为一种能精细刻画局部水流运动过程的小尺度模型被提出,其非结构化网格能极大程度上满足小尺度空间离散的需求,此外自适应时间步长方法能高效处理小尺度大水力梯度及剧烈时变源汇项。与此同时,由于S3D模型尚处于开发阶段,计算效率有较大的优化和提升的空间。考虑到不同数值算法在数据封装和矩阵求解方法上的差异,本文耦合模型的计算效率难以简单通过计算耗时进行评价。表1对比了各算例中本文模型与参照模型的时间步数、节点总数、计算耗时和平均绝对水头误差的统计结果。相比传统单一尺度高密度网格模型,本文模型能将矩阵规模和求解工作量减少90%以上,并在一定程度上降低计算耗时,同时在局部尺度复杂水流运动过程的模拟中保持较高的求解精度。
4 结论
针对传统单一尺度模型在模拟大区域含水层中的小尺度复杂水流运动过程上的不足,本文建立了一种能进行多时空尺度非匹配自由网格模拟的多网格耦合模型。通过一系列数值试验,验证了该模型在带有小尺度特征的大水力梯度问题的模拟上具有良好的适应性和计算精度。相比传统单一尺度模型方法,本文模型在区域大尺度和局部小尺度水流问题的求解上进行了空间和时间尺度的分离,有利于不同尺度模型的稳定性和收敛性。而非匹配自由时空网格耦合方法的应用,则极大地保证了本文模型对局部尺度问题中复杂边界条件及源汇项和非均质含水层参数的高效数值离散,且子域模型网格可自由划分及加密,能较大程度上降低网格节点数量并提升局部问题的求解精度。
为了更准确地刻画大区域含水层中的小尺度复杂水流运动过程,本文模型需要对模型中不同水力参数、边界条件、初始条件和源汇项进行尺度匹配,进一步的研究可将升尺度和降尺度方法联合运用到不同尺度模型之间的信息交互中,以提高模型在长时间序列模拟中的稳定性和可靠性。此外,由于小尺度模型中需要考虑非达西流的近似解析解[24],目前S3D模型尚不能精确模拟抽水井附近小范围内的井流。通过本文模型来精细刻画局部尺度复杂水流运动过程,对于模拟小尺度复杂的溶质运移、饱和-非饱和水量交换、作物根系吸水等过程具有重要意义。
参 考 文 献:
[1] 张祥伟,竹内邦良.大区域地下水模拟的理论和方法[J].水利学报,2004(6):7-13.
[2] DURLOFSKY L J,JONES R C,MILLIKEN W J.A nonuniform coarsening approach for the scale-up of displace⁃ment processes in heterogeneous porous media[J].Advances in Water Resources,1997,20(5):335-347.
[3] KARIMI-FARD M,DURLOFSKY L J.Accurate resolution of near-well effects in upscaled models using flowbased unstructured local grid refinement[J].Spe Journal,2012,17(4):1084-1095.
[4] TREFRY M G ,MUFFELS C.Feflow:A finite-element ground water flow and transport modeling tool[J].Ground Water,2007,45(5):525-528.
[5] LIN L,YANG J,ZHANG B,et al.A simplified numerical model of 3-D groundwater and solute transport at large scale area[J].Journal of Hydrodynamics,2010,22(3):319-328.
[6] ODMAN M T,RUSSELL A G.On local finite-element refinements in multiscale air-quality modeling[J].Envi⁃ronmental Software,1994,9(1):61-66.
[7] PANDAY S,LANGEVIN C D,NISWONGER R G,et al.MODFLOW-USG version 1:An unstructured grid ver⁃sion of MODFLOW for simulating groundwater flow and tightly coupled processes using a control volume finite-dif⁃ference formulation[R].US Geological Survey,2013.
[8] LEAKE S A,CLAAR D V.Procedures and computer programs for telescopic mesh refinement using MODFLOW[R].Center for Integrated Data Analytics Wisconsin Science Center,1999.
[9] BOOTH C J,BREUERE P.Using MODFLOW with TMR to Model Hydrologic Effects and Recovery in the Shal⁃low Aquifer System Above Longwall Coal Mining[C]//10th IMWA Congress:Mine Water and the Environment.Karlocy Vary,Czech Republic,2008.
[10] MEHL S W,Hill M C.MODFLOW-LGR—Documentation of Ghost Node Local Grid Refinement(LGR2)for Multiple Areas and the Boundary Flow and Head(BFH2)Package[R].Section A Ground Water in Book Model⁃ing Techniques,2013.
[11] 杨杨,邵景力等,基于LGR的不规则MODFLOW模型嵌套技术研究[J].水文地质工程地质,2015(1):22-28.
[12] MEHL S,HILL M C.Development and evaluation of a local grid refinement method for block-centered finite-dif⁃ference groundwater models using shared nodes[J].Advances in Water Resources,2002,25(5):497-511.
[13] HARBAUGH A W.MODFLOW-2005,the US Geological Survey modular ground-water model:The ground-wa⁃ter flow process.2005:US Department of the Interior[R].US Geological Survey Reston,VA,USA,2005.
[14] 陈皓锐,高占义,王少丽,等.基于MODFLOW的潜水位对气候变化和人类活动改变的响应[J].水利学报,2012,43(3):344-353.
[15] VERMEULEN P T M,HEEMINK A W,ESTROET C B M T.Reduction of large-scale numerical ground water flow models[C]//Computational Methods in Water Resources Proceedings.Elsevier Science Bv:Amsterdam.2002,397-404.
[16] 刘路广,崔远来.灌区地表水-地下水耦合模型的构建[J].水利学报,2012,43(7):826-833.
[17] JEPPESEN J,CHRISTENSEN S.A MODFLOW infiltration device package for simulating storm water infiltration[J].Groundwater,2015,53(4):542-549.
[18] ZHU Y,SHI L,LIN L,et al.A fully coupled numerical modeling for regional unsaturated-saturated water flow[J].Journal of Hydrology,2012,475:188-203.
[19] ZHA Y,SHI L,YE M,et al.A generalized Ross method for two-and three-dimensional variably saturated flow[J].Advances in Water Resources,2013,54:67-77.
[20] WASSERMAN M.Local grid refinement for three-dimensional simulators[C]//SPE Symposium on Reservoir Sim⁃ulation.Society of Petroleum Engineers.1987.
[21] HAEFNER F,Boy S.Fast transport simulation with an adaptive grid refinement[J].Ground Water,2003,41(2):273-279.
[22] FORSYTH P,SAMMON P.Practical considerations for adaptive implicit methods in reservoir simulation[J].Journal of Computational Physics.1986,62:265-81.
[23] MEHL S,Hill M C.Grid-size dependence of Cauchy boundary conditions used to simulate stream-aquifer inter⁃actions[J].Advances in Water Resources,2010,33(4):430-442.
[24] 文章,黄冠华,刘壮添,等.越流含水层中抽水井附近非达西流两区模型近似解析解[J].地球科学:中国地质大学学报,2011,36(6):1165-1172.
