水力机械运行中的拍振和共振问题探讨
2017-05-07徐洪泉廖翠林王万鹏李铁友
徐洪泉,廖翠林,王万鹏,李铁友
(中国水利水电科学研究院,北京 100038)
1 研究背景
在水电站、泵站及各类旋转机械的运行中,可能会遇到各种各样的振动和压力脉动等不稳定现象,共振和拍振都可能对安全稳定运行产生非常大的危害,因而倍受关注[1]。
当两个扰动频率比较接近时,且两个振动幅值也相差不大或相等时,会产生如图1所示的拍振现象,拍振幅值可能达到或接近两个频率幅值的代数和,会产生幅值时大时小的振动现象,常伴有类似于哮喘的严重噪音,属比较严重的不稳定现象之一。该现象常见于许多旋转机械中,例如内燃机[2]、电动机[3]、机床[4]、航空发动机[5]、压路机[6]和风机[7]等等。因此,国内外各界对拍振现象都非常重视,并对此进行了广泛而深入的研究[8-9],以避免或减轻其危害。
而共振则不同,是指机械系统所受激励的频率与该系统的某阶固有频率相接近时,系统振幅显著增大的现象。对于水力机械而言,共振是非常有害的,会引起机械和结构很大的变形和动应力,甚至造成破坏性事故,在水电站运行中不乏工程实例[1,10-11]。
共振和拍振现象都比较复杂,均为两个频率共同作用的结果,看上去很相似,如果不进行深入的分析和研究,有可能形成一些似是而非的见解,影响我们对共振和拍振的认识和辨别,有可能错误地将拍振和共振混淆,误认为“共振”或“趋于共振”,夸大了拍振的危害;也可能把一些波形和拍振近似的现象误解为拍振,在制定解决措施方面产生误导,导致错误的结果。
因此,为进一步认清拍振的本来面目,防止将拍振和共振混淆,避免被假拍振误导,我们对拍振现象进行了比较深入的研究分析,发现了部分问题和现象,而这些问题和现象有可能影响对水力机械压力脉动的本质认识,需深入分析探讨,为解决这些问题扫清道路。
2 拍振
2.1 基本原理 拍振是一种多个振源系统相互干涉的振动现象,是两种频率接近、幅值也比较接近的两个扰动因素共同产生的合成扰动现象[6]。
如假定两个不同频率的周期性扰动均为正弦波,A1、A2分别为两个不同扰动分量的幅值,ω1、ω2分别为两个扰动分量的旋转角速度,φ1、φ2分别为两个扰动分量的相位角,则由这两个扰动合成的扰动如式(1)所示:
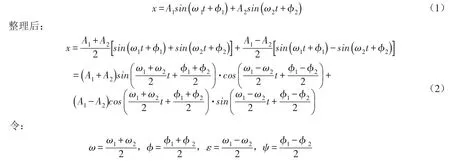
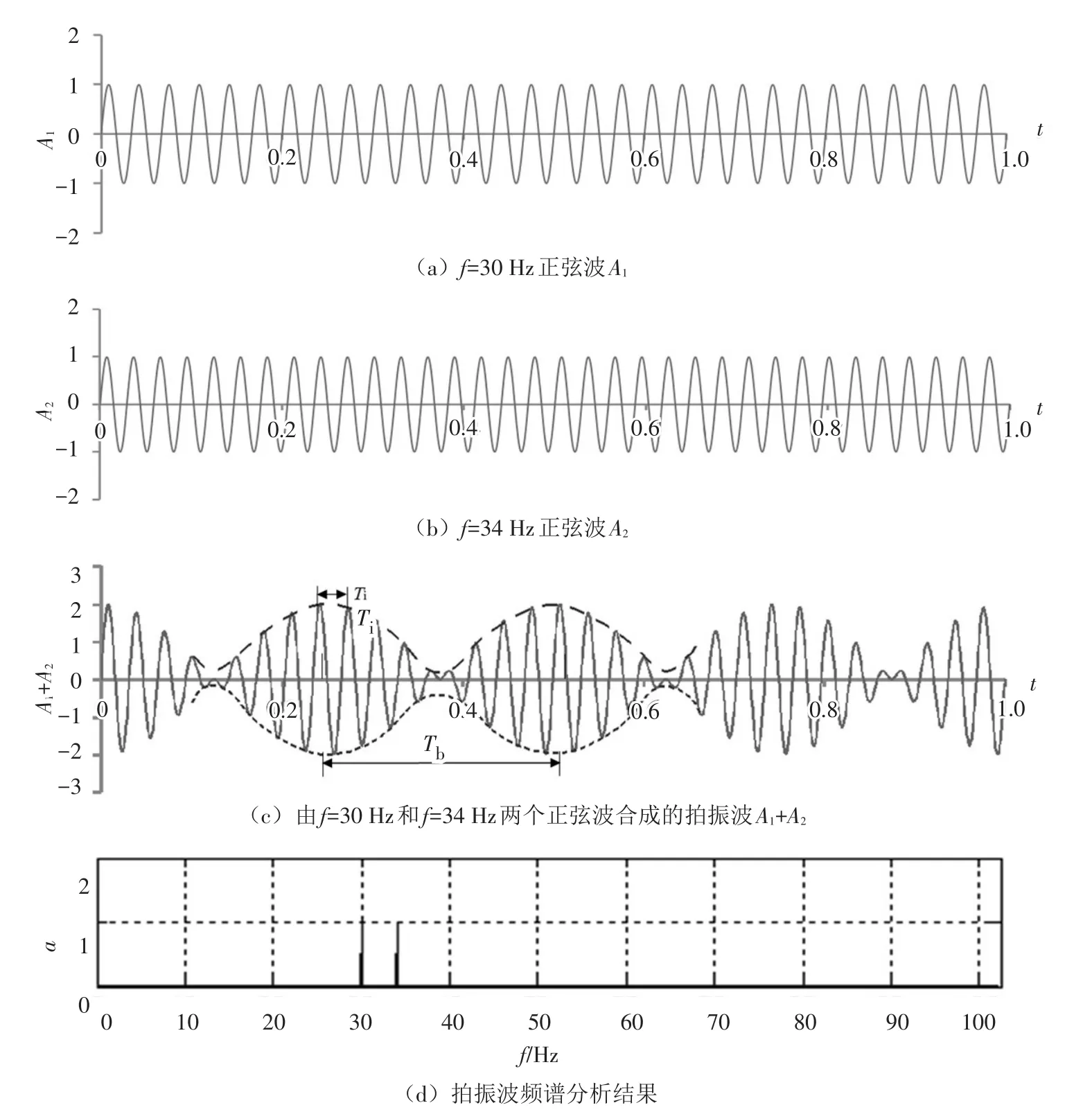
图1 两个频率相近的调谐波及其合成的拍振波、频谱分析结果
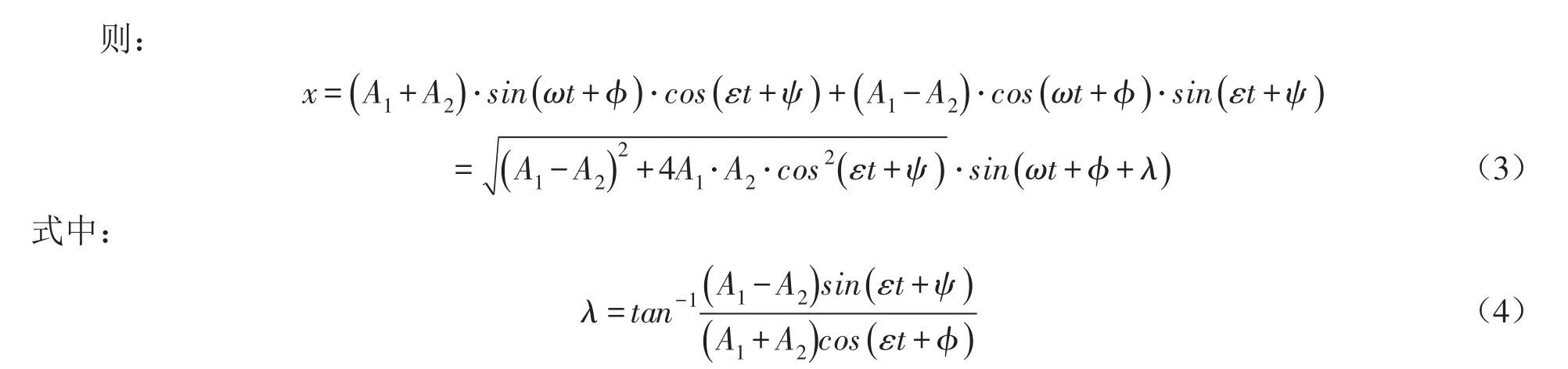
如将式(3)分解成两个部分,前一部分为幅值部分,并命:
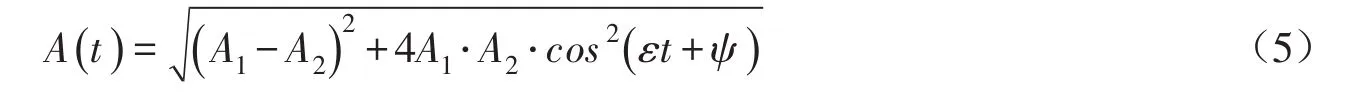
则式(3)变化为:

2.2 拍振频率 参考式(6),可如图1(c)所示将拍振波分解成两个部分,其一是变化的振动幅值A(t),是图1(c)中的虚线部分;其二是以fc为合振动频率的正弦波,在虚线勾勒出的包络线范围内波动[6]。这其中,包络线的频率即所谓的拍振频率fb:

则拍振周期:

而合振动频率:

合振动周期:

需要说明的是,拍振频率fb并不是式(5)中余弦函数的频率ε/(2π)=(ω1-ω2)/(4π),而是余弦函数频率的2倍,是因为幅值函数A(t)是一非负函数,在余弦函数值为负的半个周期内,A(t)却开启了和余弦函数值为正时相似的新周期。也就是说,A(t)的周期是余弦函数周期的一半,其频率fb自然是余弦函数频率的2倍。可能是由于误将余弦函数周期当A(t)的周期,有部分文献提出了“拍振频率是两个相近频率之差一半”的见解[1,4]。
3 拍振和共振的区别
3.1 拍振特殊情况讨论 为深入了解和认识拍振,特别是弄清拍振和共振的区别,对拍振的以下特殊情况进行讨论分析。
(1)若角速度ω1=ω2=ω,则:ε=0,式(3)变为:
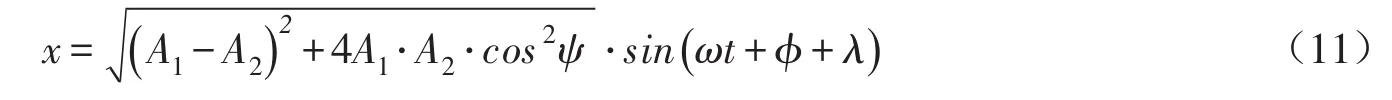
这是频率为ω的规则正弦曲线,其振幅最大值是A1+A2。也就是说,当拍振的极端情况(两个频率相等)发生时,并没有发生所谓的“共振”。这说明,共振并非拍振的一种特殊情况,两个扰动频率即使相等也不可能产生共振。
在我国的两个抽水蓄能电站中,曾遇到水泵水轮机转轮叶片和导叶动静干涉产生的压力脉动频率等于2倍工频(100 Hz),即等于发电电动机磁极个数与转频的乘积。这两个电站转速n=333.3 r/min,转速频率fn=5.555 Hz,发电电动机18个磁极,磁间隙引起的振动频率f=5.555×18=100 Hz。水泵水轮机转轮叶片数Zr=9,活动导叶数Zg=20,其转轮叶片过流频率fr=50 Hz。在其中一个的模型试验中,固定导叶间水轮机工况压力脉动的频谱分析结果如图2所示,其主频为叶片过流频率的2倍,对于真机而言也是100 Hz。但是,由于电磁激振频率和水力激振频率都是扰动频率,两者即使频率相同,其合成的振动也不是共振,只不过是拍振的特殊情况,其最大值不可能超过两个扰动幅值的代数和。实际情况也是如此,这两个电站尽管机组振动和厂房振动都比较大,噪声也比较严重,但没有发生共振。
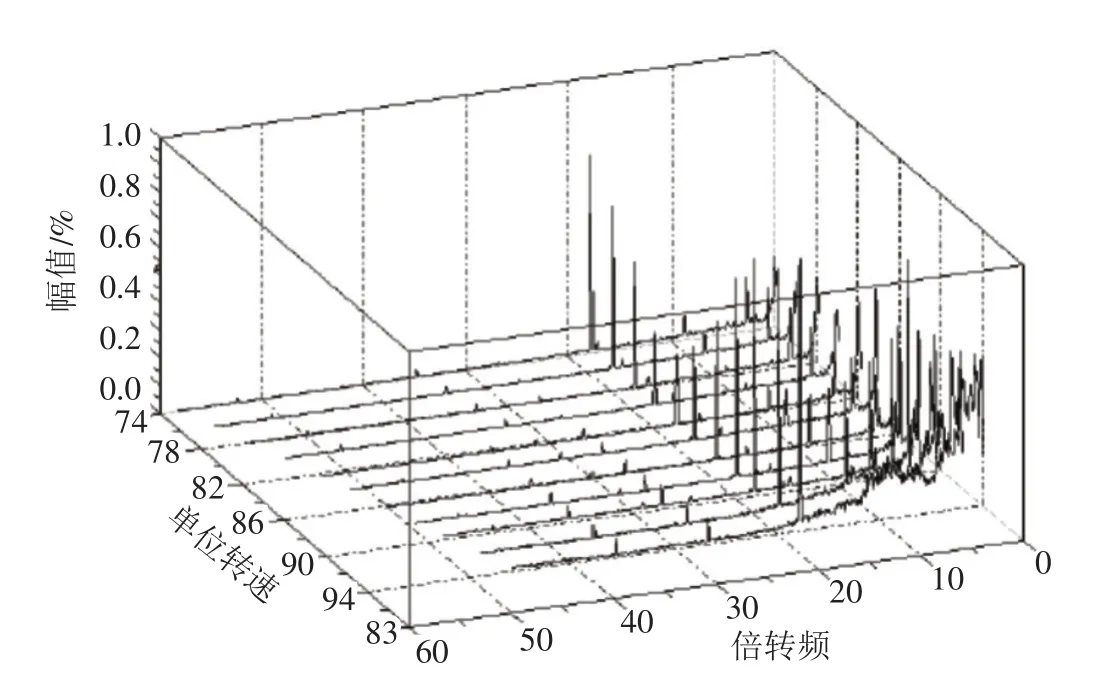
图2 某水泵水轮机在水轮机工况下固定导叶间模型压力脉动频谱曲线
(2)若ω1≠ω2,根据式(5)的包络线方程计算的拍振有如下两个极端值:
也就是说,在一般情况下,拍振振幅在A1+A2和|A1-A2|之间周期性变化。
3.2 关于共振与拍振的区别 如前所述,共振是激振频率接近甚至等于固有频率时发生的物理现象,而拍振则是两个相近扰动频率共同扰动下发生的物理现象。二者之间本质的区别不在于共振的两个频率比拍振的两个频率离得远还是近,而在于后者的两个频率都是扰动频率,前者的两个频率一个是扰动频率,另一个是固有频率。而扰动频率具有主动性,属主动频率;固有频率只能被激励或扰动,不具有主动性,属被动频率。
但是,也有观点认为,拍振也可能是激振频率接近但不等于系统固有频率[4]的干涉现象,因此而提出这两个频率“接近时产生拍振,相等时产生共振”的见解。其实不然,一个扰动频率和与其相近的固有频率不可能形成拍振,这是因为固有频率是被动的频率,其只能被激发,不能主动起作用。当该固有频率被扰动频率激励时,其只能以扰动源的频率被激振,此时系统内只有一个频率,没有两个频率,不满足拍振必须的“两个频率”条件,自然不能产生拍振。因此,拍振就是拍振,共振就是共振,不能将二者混为一谈,拍振也不是共振的前奏。扰动频率等于固有频率会引起共振,但当二者相近时只不过会激励起幅值远低于共振振幅的单频率振动,而不是拍振。
就二者的时域振动波形而言,共振波和拍振波也存在着本质区别。在工程实践中,实际的拍振波波形和图1(c)模拟波形非常接近,差别在于多了部分杂波,也不如图1(c)规范。而实际的共振波波形和图1(a)或图1(b)所示的单一频率波形更相似,其区别在于幅值会非常大,有杂波但杂波所占比例大幅降低。通过这些固定频率的时域曲线,很难发现共振特征,也难以判断是否发生共振。在工程实践中,常遇到图3所示频率发生变化的时域曲线,可记录到共振发生过程。在图3[10,12]中,记录了小浪底电站在停机过程中水轮机叶片上的应力变化。在机组转速由60%下降到20%的过程中,叶片上产生了很高的交变应力,其频率由87 Hz过渡到55 Hz,具有明显的共振特征。通过测量该波形幅值最大区段的波长可估算共振频率。
4 拍振波的辨识
在水力机械的振动和压力脉动信号中确实存在拍振波,它们的危害也很大。但是,也确实会遇到虚假的拍振波信号,有可能对我们产生误导,需要认真辨识,谨慎处理。

图3 小浪底电站停机过程中叶片上的应变
在水力机械行业也存在这种“伪拍振”现象,至少有如下两种振动或压力脉动信号有可能被当作拍振:其一是信号频率接近信号采集频率的1/2形成的和拍振波相似的波形(见图4(a)),其二为高频信号在低频信号上的载波(见图5中的pp_502部分)。总之,这两种形状和拍振波比较接近的波形都不是真正的拍振波。
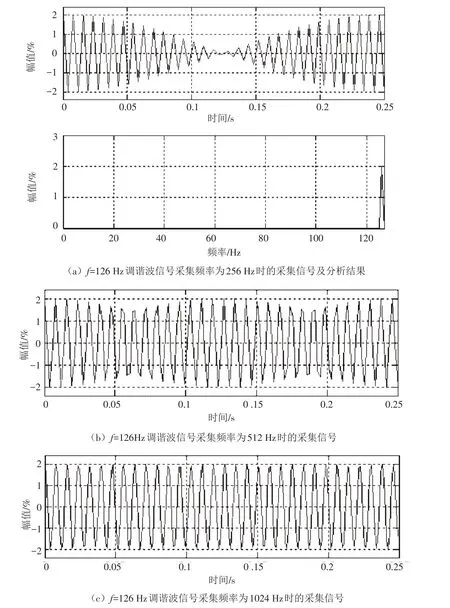
图4 f=126Hz调谐波信号采集频率不同时的采集信号比较
4.1 拍振波的特征 拍振波的特征主要包含两个方面。一是其时域曲线特征,其波动幅值时大时小,且周期性变化,总体呈现为糖葫芦形波形。二是其频率特征,其频率必须满足两个条件:首先,拍振波必须是两个相近频率波动的合成波,也就是说,在对该波形进行FFT分析后,应存在两个频率比较接近的分频f1和f2;其次,两个波动合成的拍振波的拍振频率fb应为两个相近频率之差的绝对值,即fb=|f2-f1|。
其实,葫芦形波形只是拍振波的表面特征,其频率特征才是其本质特征,据此可比较准确地区分前面介绍的两种类拍振波。
4.2 采集频率低形成的类拍振波 在采集振动或压力脉动等周期性波动信号时,如信号频率接近采集频率的1/2时,即使信号是单一频率的调谐波,其采集到的信号波形也会像图4(a)所显示的那样,呈现出与拍振波非常相似的“类拍振波”。
其实,图4(a)所示的幅值在不断变化的“类拍振波”只有一个频率(f=126 Hz),并不像真正的拍振波那样由两个相近的频率合成。之所以产生这一现象是因为其采集频率只有256 Hz,信号频率f非常接近能分析出最高频率fmax=256/2=128 Hz。正如图4(b)所示,只要将采集频率增加到512 Hz(此时fmax=512/2=256 Hz),其采集信号基本消除“类拍振波”特征。如像图4(c)所示,将采集频率增加到1024 Hz,fmax=512 Hz,同一信号的采集结果则全无拍振波特征。这说明,为避免类似的类拍振波出现,提高信号采集频率是最好的办法。
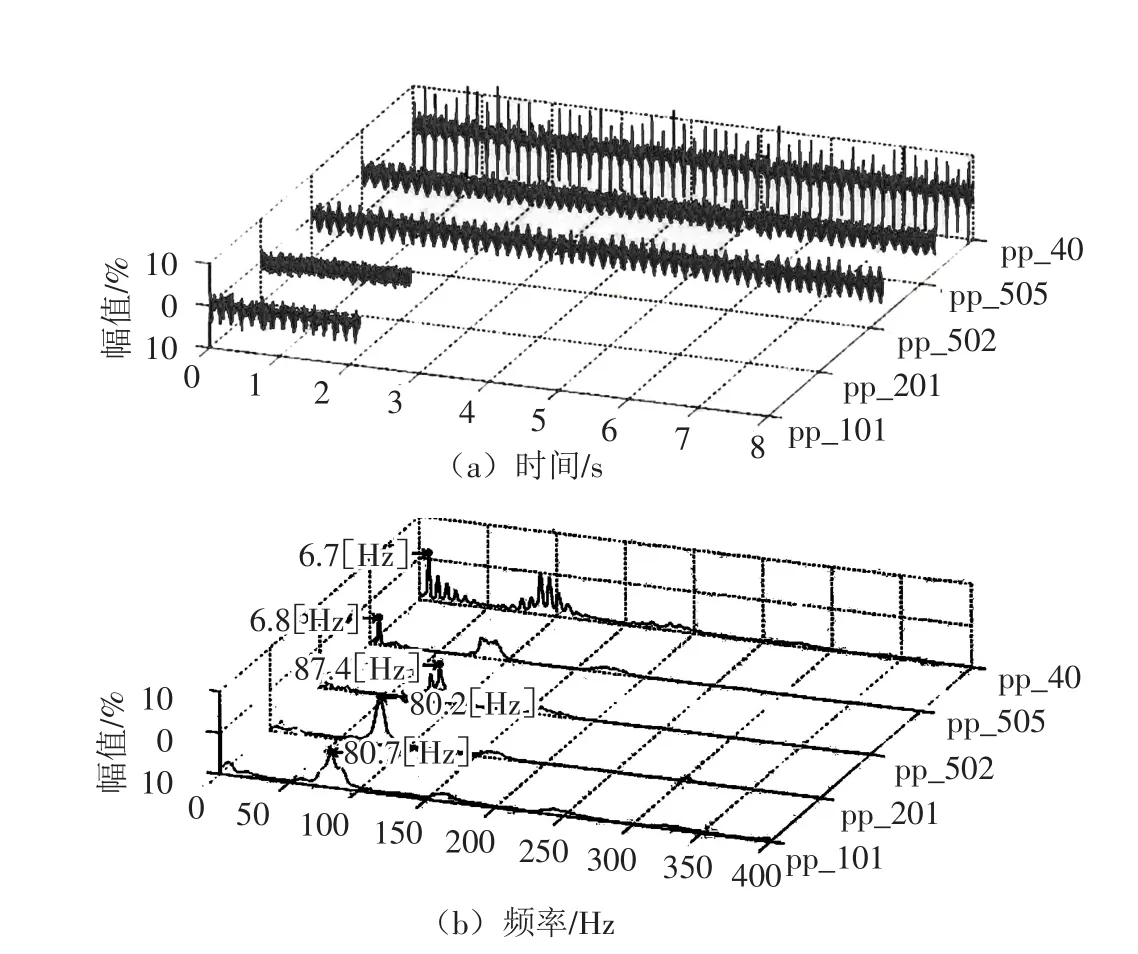
图5 某混流式水轮机模型压力脉动
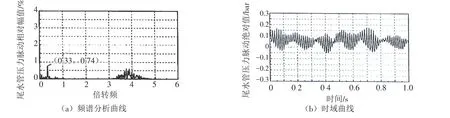
图6 某混流式水轮机尾水管锥管压力脉动
4.3 高频载波现象 在水力机械实际测量的压力脉动信号中,常遇到图5中pp-502位置所示的压力脉动信号,其波形和图1所示的真实拍振波非常相似。如单凭其时域波形来辨识,很容易将其错当作拍振波,但其实质上是高频压力脉动(fH=87.4 Hz)和低频压力脉动(fL=6.8 Hz)叠加合成的“载波”现象。尽管在用FFT分析的频谱曲线中,也发现了两个高频分量(其中f1=78.7 Hz,f2=87.4 Hz),如该波形是二者合成的拍振波,其拍振频率应为Δf=f2-f1=8.7 Hz;但是,在8s时间内,该波形有近55个“类拍振波”,其频率f≈6.85 Hz,与分析出的低频fL(即涡带频率)非常接近,故可认为其为高频分量在低频分量上的载波,而非真正的拍振波。因此,在对压力脉动或振动信号进行采集和分析时,当在其时域曲线中发现如图5(pp-502位置)等和图1比较相似的所谓“类拍振波”(整体呈糖葫芦形,幅值周期性变化)时,应加以区别辨识,不能想当然地将其作为拍振波处理。
与其类似,图6所示的压力脉动波形也和拍振波比较接近,其高频波频率为66 Hz,是转频fn(fn=17.8 Hz)的3.71倍,其附加到涡带频率(0.33fn)上,就形成了图6所示波形。其低频部分为涡带频率,其传递方式为随波逐流;高频部分为涡带自转频率的叶片倍数,其传播方式是压力波传播[13],在尾水管边壁测点测量的压力脉动幅值和该涡带离测点距离有关。离测点越远,衰减越严重,幅值越小,反之则越大,如此便形成了图5和图6所示的波形。
5 结论
(1)拍振波是两个频率相近的扰动波合成的幅值不断变化的合成波动,其最大幅值是两个扰动幅值的代数和,拍振频率是两个频率之差;(2)共振是扰动频率等于系统固有频率时发生的物理现象,当两个频率相差较小时,系统即不会发生共振,也不会发生拍振,只能以唯一的扰动频率振动;(3)两个不同的扰动波即使频率相同也不可能产生共振;(4)信号采集频率低可能会形成葫芦状波形,部分尾水管压力脉动波形也形似拍振波,对这两种“类拍振波”应区别对待。
参 考 文 献:
[1] 李启章,张强,于纪幸,等.混流式水轮机水力稳定性研究[M].北京:中国水利水电出版社,2014.
[2] 贺小龙,张立民,邱飞力,等.内燃动车组辅助机组拍振现象分析[J].噪声与振动,2016(1):83-87.
[3] MA Yunpeng.Analysis of the beat vibration for AC induction motor[J].S&M Electric Machines,1985(6):16-20.
[4] 卞斌,刘淑琴,贺恩艳,等.磁悬浮轴承磨床电主轴中拍振现象的分析[J].山东大学学报,2012,42(3):133-137.
[5] 韩军,高德平,胡绚,等.航空发动机双转子系统的拍振分析[J].航空学报,2007,28(11):1369-1373.
[6] 徐倩.双钢轮振动压路机拍振现象研究[D].西安:长安大学,2011.
[7] 姚运仕,冯忠绪,马芳武,等.冷却风扇“拍振”对转向盘抖动影响的研究[J].广西大学学报:自然科学版,2011,36(2):211-215.
[8] 赵晴,贾民平,黄跃光,等.回转机械中的拍频分析[J].东南大学学报,2003,33(1):312-315.
[9] 游斌,吴彦东,马丽华,等.多联机双风轮系统拍振分析与性能优化研究[J].工程热物理学报,2011,32(2):223-226.
[10] 胡宝玉,张立新,钟光华,小浪底转轮叶片裂纹原因分析及处理措施[J].中国水利,2004(12):41-43.
[11] 李启章,大朝山转轮叶片的卡门涡共振[M]//第十五次中国水电设备学术讨论会论文集.西宁:青海人民出版社,2004.
[12] 黄源芳,刘广宁,樊世英.原型水轮机运行研究[M].北京:中国电力出版社,2010.
[13] 徐洪泉,王万鹏,廖翠林,等.空腔危害及压力脉动传递机理研究[C]//第二十次中国水电设备学术讨论会论文集.2015:377-385.
