基于离散元的颗粒材料三维临界状态与剪胀特性研究
2017-05-07刘嘉英常晓林
刘嘉英 ,马 刚 ,周 伟,常晓林
(1.武汉大学 水资源与水电工程科学国家重点实验室,湖北 武汉 430072;2.水工岩石力学教育部重点实验室,湖北 武汉 430072)
1 研究背景
临界状态是砂土等颗粒材料变形过程中达到的极限状态。经过几十年的发展,Roscoe等[1]提出的临界状态理论[2]已成为砂土本构框架的重要组成部分。剪胀性也是砂土、粗粒土等颗粒材料的一个重要特性。经典的应力剪胀理论[3]构建了土体的变形特性与应力状态之间的关系,被广泛应用于砂土弹塑性本构模型中,但忽略了其内部结构特性对剪胀的影响[4]。因此,不少学者[5-9]引入不同形式的状态参量,提出了状态相关的剪胀模型,并建立了相关的本构关系。如Li等[7-9]引入了与临界状态孔隙比相关的状态参量,所提出的剪胀模型在Toyoura砂的室内试验中得到了验证。
目前常采用常规三轴试验研究砂土等颗粒材料的力学特性,大多数的本构模型、经典临界状态理论等也建于此基础上。而在实际工程中,由于各种因素的影响,砂土等材料常处于三向不等的应力状态,属于典型的三维问题。真三轴试验是研究土体三向不等应力状态的重要手段,Lade等[10-15]分别对Monterey砂、Santa Monica Beach砂、Nevada砂进行了真三轴试验,研究了强度、变形、剪切带以及各向异性等问题。扈萍等[16]、张敏等[17]、施维成等[18-19]研究了中主应力系数对粉细砂、福建标准砂及粗粒土应力-应变关系及强度指标的影响。然而受试验条件的限制,真三轴物理试验能够加载到临界状态且不产生局部化变形的很少[20]。此外,离散单元法(DEM)[21-26]、连续-离散耦合方法(FDEM)[27-29]等非连续介质力学方法,使得从宏细观两个层面研究了砂土、粗粒土等颗粒材料在三维应力条件下的变形和强度特性成为可能。
在三维应力条件下,颗粒材料的临界状态和剪胀特性有别于轴对称的应力条件,然而受限于试验条件等因素,所涉及的研究不多且存在一些不同看法。关于颗粒材料在三维应力条件下临界状态线的唯一性,学术界没有一致的结论,如Zhao等[30]根据离散元数值试验结果,认为颗粒材料在三维应力条件下临界状态线有唯一性,但Huang等[31]同样采用离散元方法,却得出不同中主应力系数对颗粒材料临界状态线有所影响的结论。而在理论上[32]、室内试验[18]中,关于临界状态线的唯一性亦有不同的论述。此外,砂土等颗粒材料在三维应力条件下的剪胀特性亦较为复杂,不同的学者采用不同的方法,对颗粒材料的剪胀特性进行了多种数学描述。施维成等[18-19]、Xiao等[33-34]根据粗粒土真三轴试验结果,研究了三维空间的应力剪胀关系,并提出了多个剪胀模型。马刚等[28-29]采用连续-离散耦合的数值分析方法,研究了堆石体在真三轴应力路径下的非共轴性和剪胀特性。总体而言,尽管在颗粒材料三维应力条件下的临界状态和剪胀特性方面有了一些研究成果,但由于缺乏足够的试验数据,仍需要作进一步的研究和探讨。
砂土等颗粒材料是由大量离散的固体颗粒相互作用组成的复杂体系,采用细观数值模拟方法(如离散单元法DEM)可以再现颗粒材料的宏观力学特性,并揭示其复杂力学特性背后的细观机理。在细观数值模拟中,在对颗粒的形状、级配和接触特性等做了一些简化,但其能准确控制试样的级配、排水等条件,精确实现预定的加载条件和加载路径,避免试样在加载过程中受外界因素的影响。采用周期性边界控制试样的加载,能够最大程度地避免剪切带的产生,使试样整体能够在剪切过程中达到临界状态。
本文将基于颗粒离散元方法,采用开源软件LIGGGHTS(LAMMPS Improved For General Granular and Granular Heat Transfer Simulations)[35]进行多组颗粒材料的真三轴数值试验,研究了中主应力对颗粒材料剪胀特性和临界状态的影响。根据离散元数值试验数据,分析三维应力条件下颗粒材料临界状态的唯一性,对Li等[8]提出的状态相关剪胀方程进行验证,并通过角隅函数修正三维情况下的模型参数,为建立合理的颗粒材料本构模型提供一定的参考。
2 真三轴数值试验
2.1 周期性边界应力控制 进行DEM模拟时,不同的边界条件会对颗粒材料的力学响应有一定的影响。刚性边界、柔性边界以及周期性边界为较为常用的边界条件。本文研究需要将试样加载到临界状态,并尽量避免应变局部化现象的发生。周期性边界条件下,边界溢出颗粒将循环出现在对称的边界上。采用周期性边界进行数值模拟,能够反映局部推广到整体的性质,减小试样在加载过程中受边界的影响,并且使试样在空间中保持较为均匀的应变场[21,31]。因此本文采用周期性边界进行真三轴数值试验。

采用周期性边界进行应力控制时,颗粒集合体的应力张量可以表示为:式中:V为体积单元的体积;Np为体积单元内颗粒的数量;为颗粒p的应力张量;Vp为颗粒p的体积。
在对周期性边界进行应力控制时,Thornton等[36]、Huang等[31]采用控制加载过程中应变率的方法,使颗粒集合体的应力状态(由式(1)计算所得)达到预定的值以满足真三轴应力路径。本文应用Huang等[31]的算法进行周期性边界应力控制,加载过程中各个方向的应变率采用如下方法控制:

式中:ε˙为试样加载的应变率;σ*为试样在某方向需要达到的应力值;σ为当前的应力值;g为增益参数;ε˙max为加载过程中允许的最大应变率。通过试算得到合适的ε˙max,使应变率ε˙在加载过程中合理变化,从而使颗粒集合体的应力状态符合预定的应力路径。
2.2 数值试样与参数 制样时,首先在立方体空间随机生成19 436个无接触的圆球颗粒,粒径分布如图1所示,平均粒径d50为6.25 mm。为了避免由制样产生的初始各向异性,首先在试样的各个方向采用位移控制等速地压缩试样直至目标大小,然后给试样施加三向等压应力直至达到预定的围压值。本文数值试验考虑了6个级别的围压(0.5、1.0、2.0、4.0、8.0和16.0 MPa),其对应的初始孔隙比、平均配位数如表1所示。在数值试验中不考虑重力,采用位移等速压缩进行制样,与室内试验有所区别,但这种制样方法能减小制样过程产生的各向异性,生成初始各向同性数值试样,从而避免加载过程中试样的原生各向异性的影响。
颗粒间接触模型采用Hertz-Mindlin模型,并引入了转动阻抗[37],即在颗粒动力平衡系统中添加一个转动阻力矩,采用转动摩擦系数控制材料的抗转动特性。本文数值试验采用的细观参数如表2所示。

图1 数值试样与粒径分布
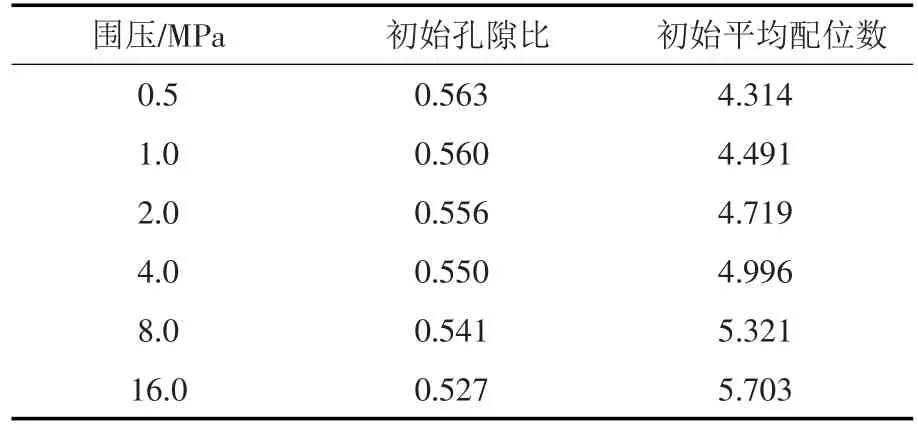
表1 不同围压试样表

表2 数值模拟细观参数
2.3 真三轴加载路径 采用中主应力系数b或应力罗德角θσ反映3个主应力之间的关系:

式中:中主应力系数b的取值范围为0≤b≤1。当b=0时,σ2=σ3,应力罗德角θσ=0,试样处于三轴压缩状态;当b=1时,σ2=σ1,应力罗德角试样处于三轴拉伸状态。本文进行的真三轴数值试验的b值分别取为0.0,0.25,0.5,0.75和1.0。
采用应力不变量广义剪应力q、平均静水压力p描述颗粒材料的应力状态:

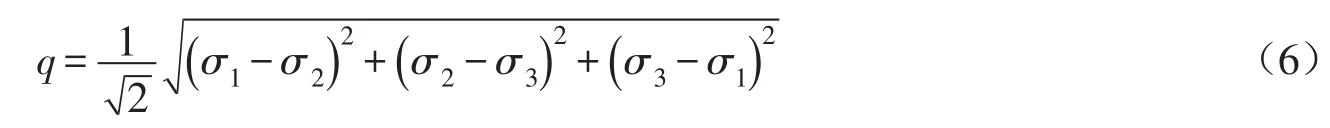
体积应变εv、剪应变εq用3个主应变表示为:
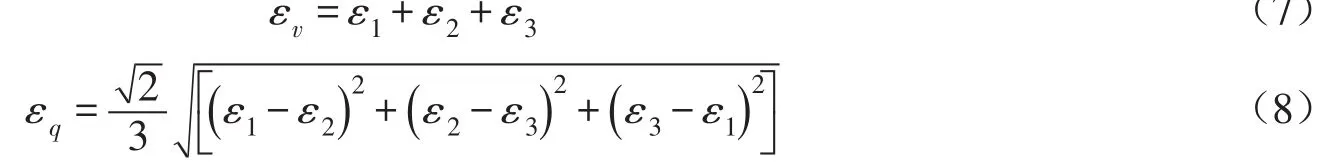
本文通过控制周期性边界的移动速率来控制试验各个方向应力的大小。进行等p等b数值试验时,施加在试样上的中主应力σ2和小主应力σ3分别为:
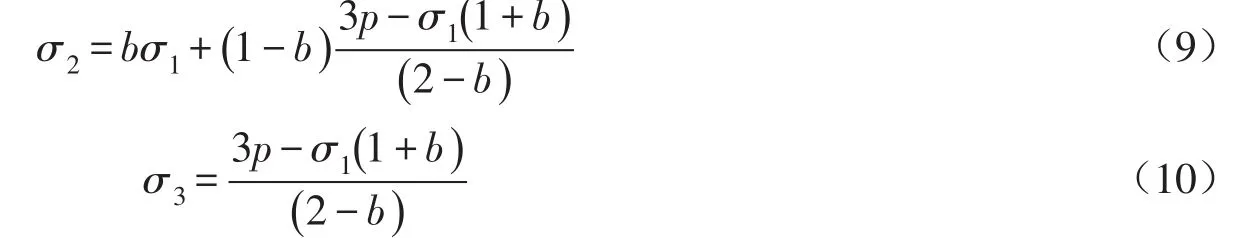
进行等σ3等b数值试验时,小主应力σ3不变,施加在试样上的中主应力σ2为:

2.4 宏观力学响应 初始围压为0.5 MPa的等p等b数值试验结果如图2、图3所示,各试样在加载过程中保持平均应力p=0.5 MPa。
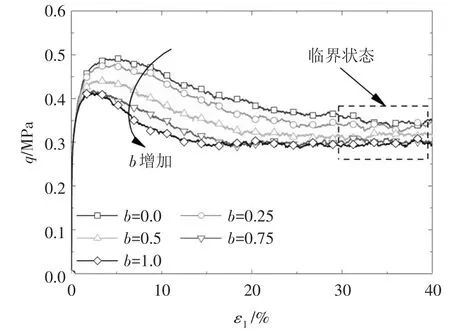
图2 不同加载路径的广义剪应力演化曲线
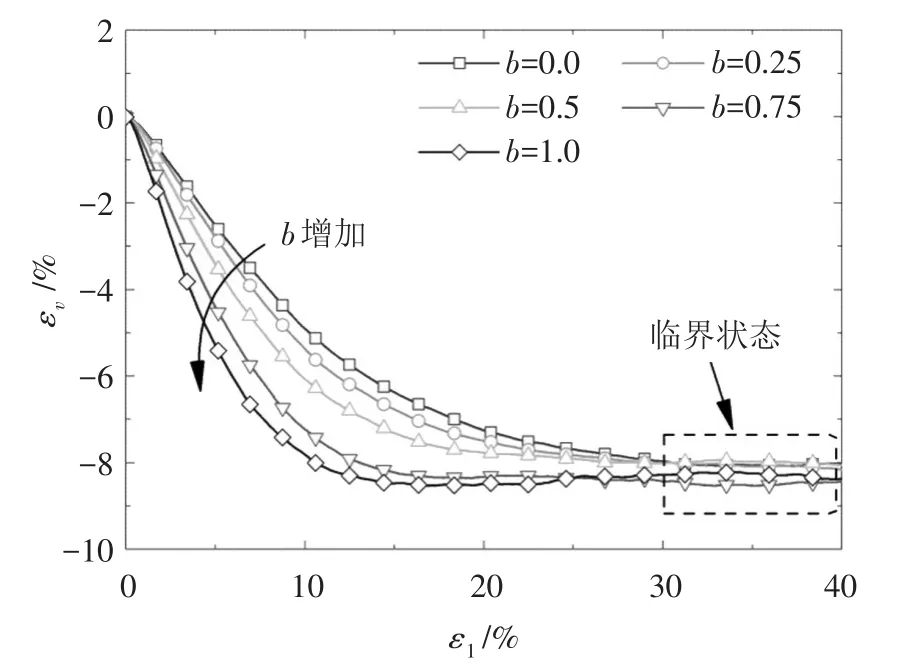
图3 不同加载路径的体积应变演化曲线
图2为广义剪应力q随大主应变ε1的演化曲线。中主应力系数的影响体现在,随着b的增加,峰值广义剪应力减小,其对应的大主应变和临界值也逐渐减小。图3为体积应变εv随大主应变ε1的演化曲线,体积应变以剪缩为正,剪胀为负。由于试样比较密实,且不可破碎,在加载初期未出现明显的剪缩。加载过程中不同中主应力系数对应的试样均产生了明显的剪胀,且b值越大,剪胀越明显。综合图2和图3,当加载到轴向应变为30%~40%时,试样的应力状态、体积应变均不再变化,可以认为试样均达到了临界状态。
3 复杂应力路径下的临界状态
3.1 临界状态线 Li等[38]对有效静水压力进行归一化,提出了砂土等无黏性颗粒材料的临界状态线表达式:

式中:ec、p′c分别为临界状态下的孔隙比与有效静水压力;pa为标准大气压;eΓ、λ、ξ为模型参数。根据式(12)拟合不同初始围压下等p等b、等σ3等b应力路径试验得到的临界状态点,得到的临界状态线如图4所示。拟合参数值eΓ=0.699,λ=0.0002,ξ=0.971。由图4可见,不同中主应力系数对应的临界点有所离散,但离散程度较低,基本落在拟合临界线附近。而在对式(12)进行数据拟合时,其相关系数达到0.96,因此,本文认为,在不同的中主应力系数的真三轴试验,其临界状态线CSL是唯一的。
对于真三轴加载路径下临界状态线的唯一性问题,目前的研究存在一定分歧。Zhao等[30]认为临界状态线是唯一的,与中主应力系数无关,而Huang等[31]则认为临界状态线与中主应力系数相关。将Zhao等[30]、Huang等[31]的临界状态数据点绘于图5中。二者数值模拟所得的临界状态数据点在e-lgp平面内的临界状态线附近也仅有较小的离散,二者结论的差异可能是因为其临界状态线的坐标取值范围不同而造成的。Huang等[31]对于不同中主应力系数的临界状态数据较大的离散性,可能是因为其计算所得的临界状态孔隙比变化范围较小,从而使同一围压下对应的孔隙比的随机性差异放大所致。而在图5中,在孔隙比变化较大的坐标范围下,Huang等[31]的不同的临界状态线也基本重合。Li等[32]也通过理论证明了临界状态线(CSL)的唯一性,因此可认为本文对临界状态线的唯一性的认识是合理的。本文的后续工作也是基于临界状态线唯一性的前提。
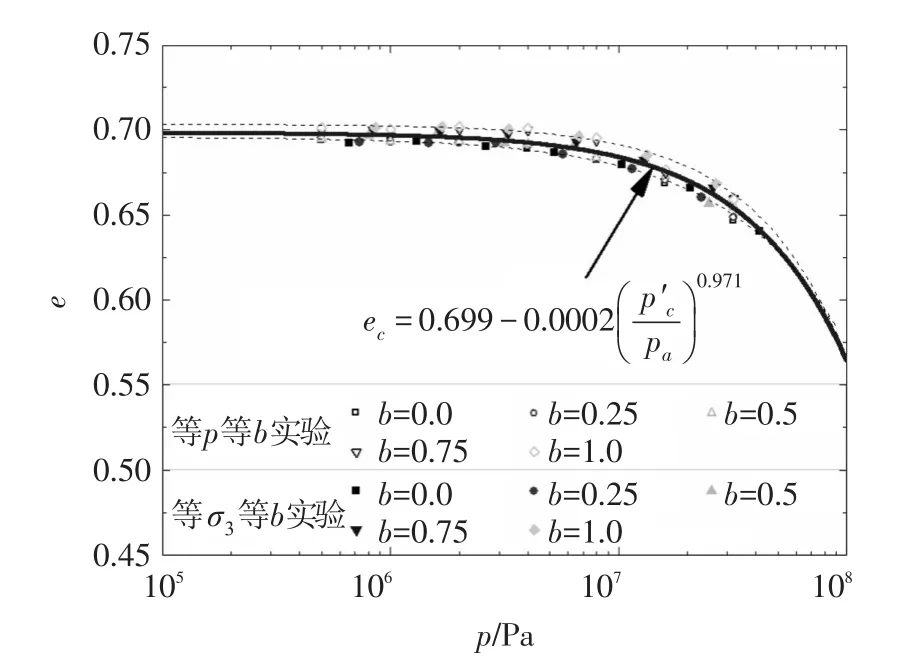
图4 临界状态线
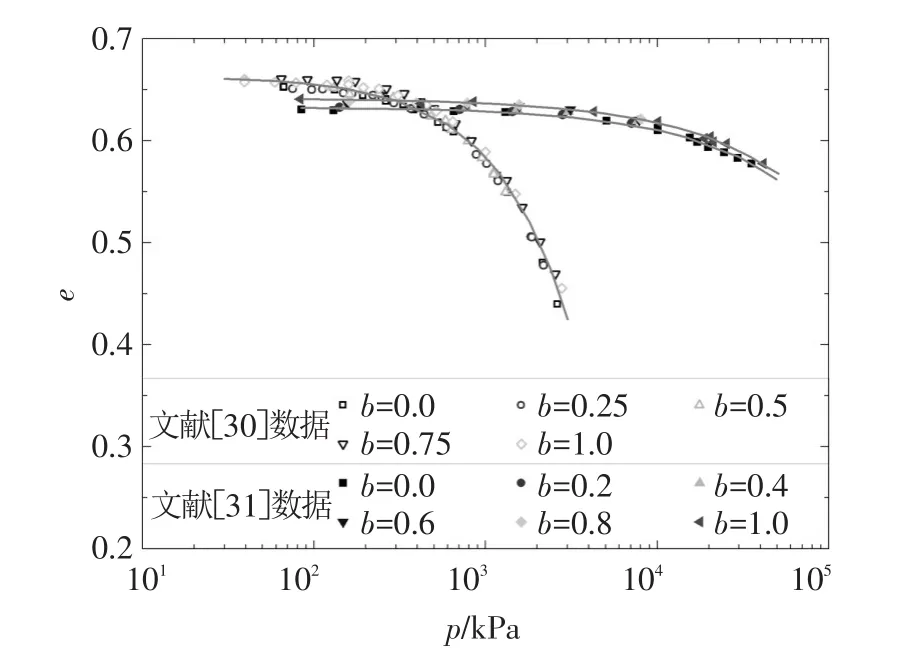
图5 其他文献中的临界状态数据
3.2 临界应力比 为了反映中主应力对应力比的的影响,一般将临界应力比M表示为应力罗德角θσ的函数

式中Mc为三轴压缩条件(b=0)对应的临界状态应力比。
角隅函数g(θσ)有多种形式,本文数值试验中试样的摩擦角较小(φ<22°),因此,采用形式较为简单的角隅函数即可满足不同应力罗德角对应的应力比关系[39]
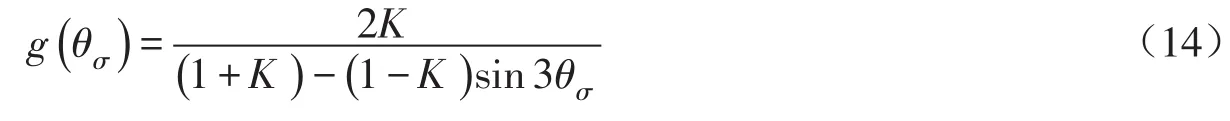
式中K为三轴拉伸与压缩条件下的临界状态应力比的比值。
将数值试验得到的临界应力比与式(13)预测的临界应力比绘于π平面内,如图6所示。可以看出,根据公式计算所得的临界应力比与数值试验结果基本一致。关于颗粒材料在三维条件下临界状态线以及临界状态应力比的规律,与以往的试验研究结果相似,也进一步验证了本文离散元数值模拟结果的合理性。
4 真三轴试验的剪胀特性
4.1 状态相关剪胀模型 在三维应力空间,颗粒材料的剪胀因子d定义为塑性体变增量与塑性剪应变增量之比:

砂土等无黏性颗粒材料的剪胀特性不仅与应力比有关,还与材料的内部结构有关。Been等[40]将砂土的临界状态作为参考状态,定义了状态参量ψ,其值为当前有效静水压力下的孔隙比e与临界孔隙比ec之差:

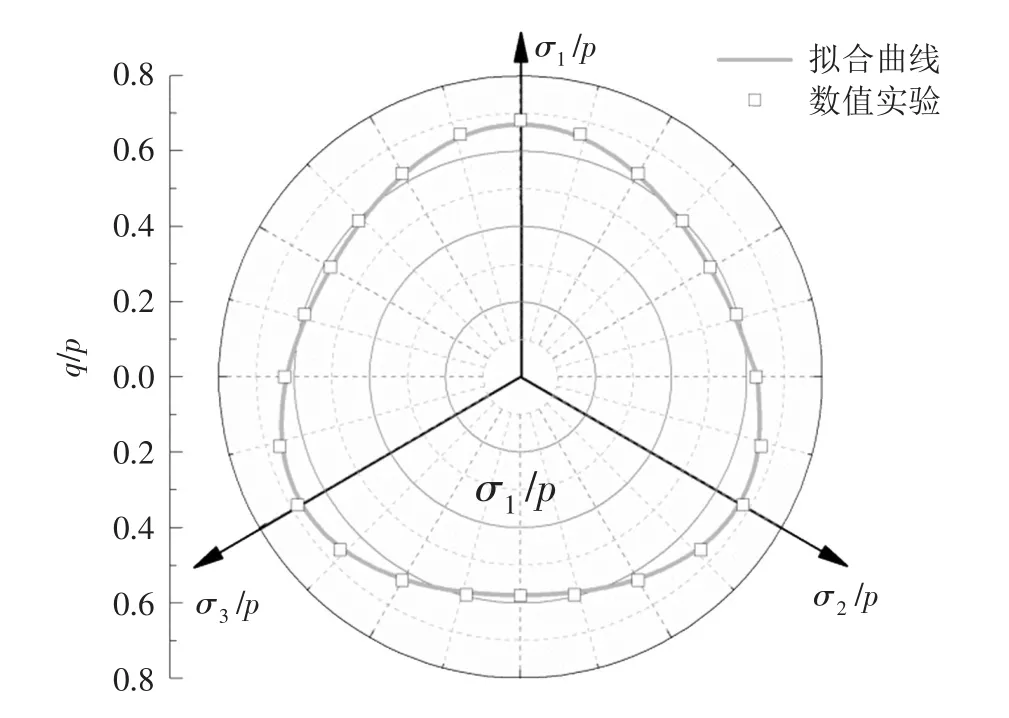
图6 π平面内临界状态应力比
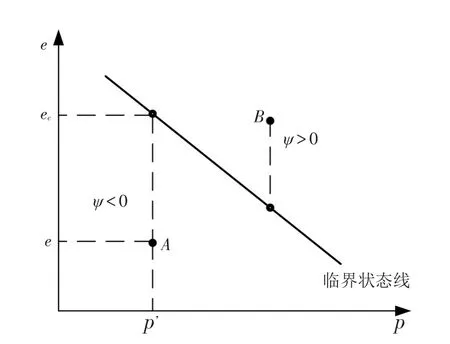
图7 状态参数量示意
图7为状态参量在e-p平面内的示意,A点在临界状态线下方,ψ<0,表示砂土的状态较为紧密,剪切时会发生剪胀;B点在临界状态线上方,ψ>0,表示砂土的状态较松,剪切时会发生剪缩。
在经典剑桥模型中,应力剪胀关系表示为d=M-η,其中M为临界状态应力比,η为当前应力比。此模型未考虑砂土的内部状态。Li等[8]提出了基于状态相关的砂土剪胀模型,将剪胀因子d与应力比η的关系表示为:
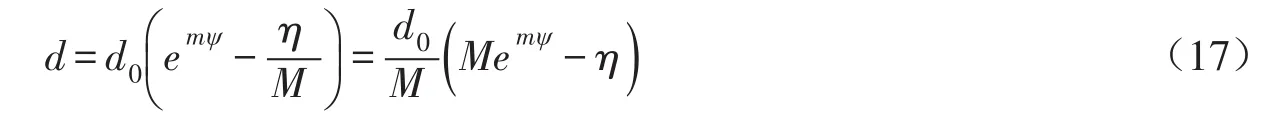
式中d0和m为模型参数,可从常规三轴试验结果得到。当M=0d0=M时式(17)还原为剑桥模型的剪胀方程。
采用围压0.5 MPa,b=0条件下的等p等b数值试验数据,根据式(17)进行拟合,得到m=4.570,d0=0.619。将式(17)预测的d-η关系曲线绘于图8。由于本文数值试验采用的试样较为密实,因此d-η曲线存在一个明显的转折点,即剪胀因子在峰值应力比时达到最小值,此时试样的剪胀速率最快。在该点之前,d-η曲线大致呈直线型式;达到该点以后,应力比逐渐减小,剪胀因子逐渐增加直至为0,此时应力比和剪胀因子均不再变化,达到临界状态。除了少数数据点偏离预测值外,式(17)较为准确地预测了数值试验中剪胀因子d与应力比η的关系曲线,因此可应用状态相关剪胀理论描述颗粒材料的剪胀特性。
4.2 剪胀方程的三维化 砂土的实际应力条件并非轴对称,是典型的三维问题。Li[9]在原始模型的基础上,将剪胀模型三维化,即将式(18)中的临界应力比表示为Lode角的函数。黄茂松等[41]在构建松砂静态液化本构模型时也采用了类似的型式:

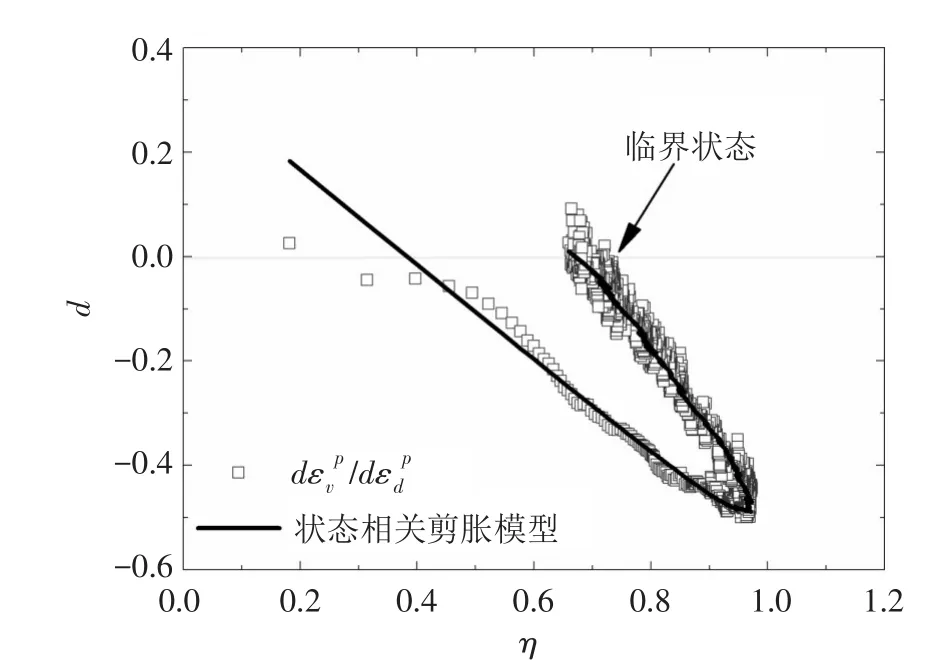
图8 三轴压缩条件下的剪胀-应力比关系
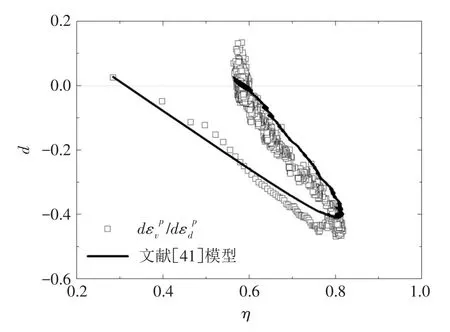
图9 b=1.0条件下式(18)预测的应力-剪胀曲线与数值实验结果对比
式(18)所描述的剪胀模型,当状态参量ψ变化很小时(如加载初期),d-η曲线近似为直线。该直线的斜率为与应力罗德角无关,即不同中主应力系数对应的d-η曲线初始段的斜率是相同的。而本文的离散元数值模拟结果表明,应力-剪胀曲线的初始段斜率是与中主应力系数有关的,如图8、图9所示。已有试验研究也表明应力-剪胀曲线的初始直线段的斜率随着应力罗德角的变化而变化[21],因此需要对三维剪胀模型进一步修正。由于颗粒材料在三维应力条件下的应力-剪胀关系跟应力罗德角有关,因此本文拟根据式(17),结合数据拟合的结果,将其中的模型参数d0和m表示为与角隅函数g(θσ)有关的形式,即:

式中d0与m为b=0.0即三轴压缩条件下的模型参数值。
采用式(19)预测中主应力系数为0.25,0.5,0.75和1.0的d-η关系曲线,将其与数值试验结果绘于图10。由图10(a)—(d)可知,根据式(19)预测的应力剪胀关系与数值试验结果基本吻合。图10(e)为不同b值对应的剪胀曲线,可以发现,在初始的近似直线段,随着中主应力系数的增加,其斜率和截距均不断增加。图10(f)对比了在中主应力系数为1.0时,本文模型与黄茂松等[41]采用模型的预测结果。由此可以明显看出,本文提出的剪胀方程在较大的中主应力系数条件下对应力-剪胀曲线的拐点及斜率预测能力较好。为量化式(18)与式(19)的拟合结果,表3给出了二者的预测值与离散元数值模拟值的平均均方差,可以看出,随着中主应力系数b的增加,文献[41]给出的模型的预测值与数值模拟结果的相离程度较大,而本文给出的公式计算所得的均方差则基本都保持在一个相对小的范围内。

表3 公式预测与离散元数值模拟的平均均方差

图10 本文模型预测的三维剪胀-应力比关系
4.3 三维剪胀模型的验证 采用不同应力加载路径的数值试验数据验证本文提出的三维剪胀模型。图11为初始围压为2 MPa的等p等b应力路径对应的剪胀曲线,图12为围压为0.5 MPa的等σ3等b应力路径对应的应力剪胀曲线。由图11、图12可知,式(19)预测的d-η关系曲线与离散元数值试验结果非常接近,且不同中主应力系数对应的应力-剪胀曲线规律与图10类似。因此,本文提出的剪胀方程在一定程度上可以描述颗粒材料在三维应力条件下的剪胀特性。
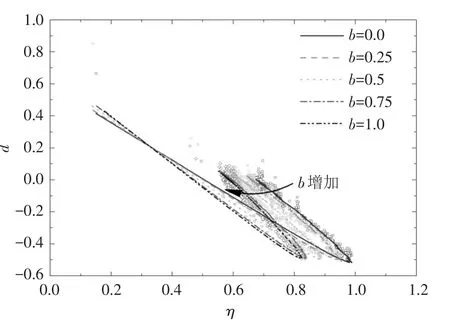
图12 等σ3等b实验对应的剪胀-应力比关系
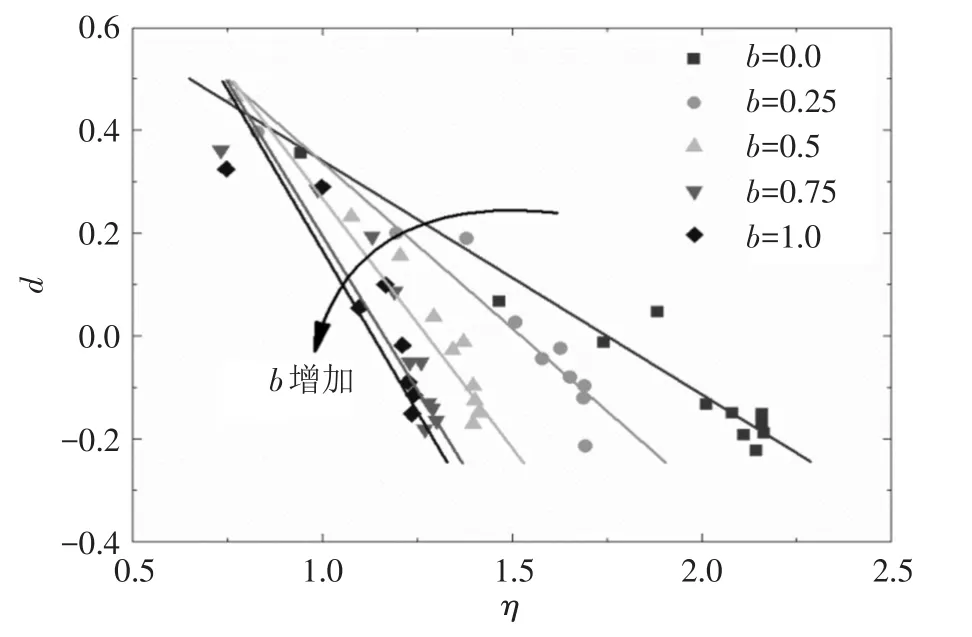
图13 Xiao等[21]的试验数据
5 剪胀模型的讨论
本文提出的基于临界状态相关的三维剪胀模型,是基于离散元数值试验建立的。该剪胀模型在初始加载直线段的规律较好。Xiao等[21]进行了堆石体真三轴室内试验,并拟合了剪胀与应力比之间的直线关系。将Xiao等[21]的实验数据绘于与本文一致的坐标中,如图13所示。可以发现直线的斜率以及截距随中主应力系数的变化趋势与本文提出的剪胀模型基本一致。由于Xiao等[21]的室内试验没有出现应变软化段,故其可以采用直线较好地描述堆石体的剪胀性。
本文提出的剪胀方程,是在Li等[8]提出的状态相关剪胀模型的基础上,将模型参数表示为角隅函数的型式。该公式可以较好地描述离散元模拟条件下的应力-剪胀关系,可以反映中主应力系数对颗粒材料剪胀特性影响的一般规律,但是其适用性以及适用范围等仍然需要更多的理论分析以及物理试验验证。
现如今关于砂土、粗粒土等材料的真三轴试验很多,然而能真正达到临界状态的真三轴试验数据并不多,因此本文没有采用更多的试验数据进行验证。笔者拟开展真三轴物理试验,采用松砂、密砂两种特征的土对本文提出的公式进行验证。
采用离散元细观数值模拟探讨颗粒材料的宏观临界状态与剪胀特性,是本文的一个尝试,希望能够从数值模拟中得到一定规律以对颗粒材料的性质有更深入的认知。颗粒材料的剪胀性从本质上是颗粒间、颗粒与孔隙等结构之间的相互影响和共同作用的结果。本文进行的数值试验及提出的剪胀方程,亦可从微观的角度进行探讨和解释,如组构量、各向异性等,进一步探讨剪胀的产生机理,从而加深对土体变形本质的认识。而在离散元数值模拟中,对于颗粒形状、颗粒尖角等因素的考量也是必要的,本文采用的转动阻抗还不足以模拟这种效应,因此对复杂颗粒形状的离散元模拟以及其对应力-剪胀关系的影响也将是笔者下一步要展开的工作。
6 结论
本文采用颗粒离散元方法,进行了颗粒材料的真三轴数值试验,分析了颗粒材料在真三轴应力状态下的临界状态和剪胀特性,主要结论如下:
(1)在等p等b真三轴应力路径加载试验中,应力应变规律符合已有的物理试验和数值模拟结果。随着中主应力系数的增大,广义剪应力的峰值和临界值均减小,体积应变在初期表现出明显的剪胀,到加载结束时基本保持不变。
(2)试样加载结束时各试样均达到了临界状态。拟合e-lgp平面临界状态线,不同中主应力系数对应的e-lgp数据点落在唯一的临界状态线附近;q-p平面的临界状态应力比可以采用角隅函数近似描述。
(3)状态相关剪胀理论可以较好地预测密实颗粒集合体的剪胀特性。通过引入角隅函数修正模型参数,提出了一个三维条件下状态相关的剪胀模型,可以近似反映真三轴应力状态下的应力剪胀关系。离散元数值结果可以从一定程度上反映颗粒材料的应力-剪胀规律,但该公式仍需更多的理论研究和物理试验验证。
参 考 文 献:
[1] ROSCOE K H,SCHOFIELD A N,WROTH C P.On the yielding of soils[J].Geotechnique,1958,8(1):22-53.
[2] SCHOFIELD A,WROTH P.Critical State Soil Mechanics[M].US:Mc Graw Hill.1968.
[3] ROWE P W.The stress-dilatancy relations for static equilibrium of an assembly of particles in contact[J].Proc R Soc London Ser A,1962,269(1339):500-527.
[4] 蔡正银,李相菘.砂土的剪胀理论及其本构模型的发展[J].岩土工程学报,2007,29(8):1122-1128.
[5] MANZARI M T,DAFALIAS Y F.A critical state two-surface plasticity model for sands[J].Geotechnique,1997,47(2):255-272.
[6] WAN R G,GUO P J.A simple constitutive model for granular soils:modified stress-dilatancy approach[J].Computers and Geotechnics,1998,22(2):109-133.
[7] LI X S,DAFALIAS Y F,WANG Z L.State-dependent dilatancy in critical-state constitutive modelling of sand[J].Canadian Geotechnical Journal,1999,36(4):599-611.
[8] LI X S,DAFALIAS Y F.Dilatancy for cohesionless soils[J].Geotechnique,2000,50(4):449-460.
[9] LI X S.A sand model with state-dependent dilatancy[J].Geotechnique,2002,52(3):173-186.
[10] LADE P V,DUNCAN J M.Cubical triaxial tests on cohesionless soil[J].Journal of Geotechnical and Geoenvi⁃ronmental Engineering,1973,101(10):793-812.
[11] WANG Q,LADE P V.Shear banding in true triaxial tests and its effect on failure in sand[J].Journal of Engi⁃neering Mechanics,2001,127(8):754-761.
[12] LADE P V,WANG Q.Analysis of shear banding in true triaxial tests on sand[J].Journal of Engineering Mechan⁃ics,2001,127(8):762-768.
[13] ABELEV A V,LADE P V.Effects of cross anisotropy on three-dimensional behavior of sand.I:Stress-strain be⁃havior and shear banding[J].Journal of Engineering Mechanics,2003,129(2):160-166.
[14] LADE P V,ABELEV A V.Effects of cross anisotropy on three-dimensional behavior of sand.II:Volume change behavior and failure[J].Journal of Engineering Mechanics,2003,129(2):167-174.
[15] RODRIGUEZ N M,LADE P V.True triaxial tests on cross-anisotropic deposits of fine Nevada sand[J].Interna⁃tional Journal of Geomechanics,2013,13(6):779-793.
[16] 扈萍,黄茂松,马少坤,等.粉细砂的真三轴试验与强度特性[J].岩土力学,2011,32(2):465-470.
[17] 张敏,许成顺,杜修力,等.中主应力系数及应力路径对砂土剪切特性影响的真三轴试验研究[J].水利学报,2015,46(9):1072-1079.
[18] 施维成,朱俊高,代国忠,等.粗粒土在π平面上的真三轴试验及强度准则[J].河海大学学报:自然科学版,2015,43(1):11-15.
[19] 施维成,朱俊高,代国忠,等.球应力和偏应力对粗粒土变形影响的真三轴试验研究[J].岩土工程学报,2015,37(5):776-783.
[20] XIAO Y,SUN Y,LIU H,et al.Critical state behaviors of a coarse granular soil under generalized stress condi⁃tions[J].Granular Matter,2016,18(2):1-13.
[21] THORNTON C.Numerical simulations of deviatoric shear deformation of granular media[J].Géotechnique,2000,50(1):43-53.
[22] NG T T.Macro-and micro-behaviors of granular materials under different sample preparation methods and stress paths[J].International Journal of Solids and Structures,2004,41(21):5871-5884.
[23] MAHMUD SAZZAD M,SUZUKI K,MODARESSI-FARAHMAND-RAZAVI A.Macro-micro responses of gran⁃ular materials under different b values using DEM[J].International Journal of Geomechanics,2012,12(3):220-228.
[24] ZHOU W,LIU J,MA G,et al.Three-dimensional DEM investigation of critical state and dilatancy behaviors of granular materials[J].Acta Geotechnica,2017,12(3):527-540.
[25] ZHOU W,YANG L,MA G,et al.Macro-micro responses of crushable granular materials in simulated true triaxi⁃al tests[J].Granular Matter,2015,17(4):497-509.
[26] 周伟,谢婷蜓,马刚,等.基于颗粒流程序的真三轴应力状态下堆石体的变形和强度特性研究[J].岩土力学,2012,33(10):3006-3012.
[27] 周伟,刘东,马刚,等.基于随机散粒体模型的堆石体真三轴数值试验研究[J].岩土工程学报,2012,34(4):748-755.
[28] 马刚,刘嘉英,常晓林,等.堆石体在真三轴应力状态下的非共轴性与剪胀特性[J].中南大学学报:自然科学版,2016,47(5):1697-1707.
[29] MA G,CHANG X L,ZHOU W,et al.Mechanical response of rockfills in a simulated true triaxial test:A com⁃bined FDEM study[J].Geomechanics and Engineering,2014,7(3):317-333.
[30] ZHAO J,GUO N.Unique critical state characteristics in granular media considering fabric anisotropy[J].Géotechnique,2013,63(8):695-704.
[31] HUANG X,HANLEY K J,O’SULLIVAN C,et al.DEM analysis of the influence of the intermediate stress ratio on the critical-state behaviour of granular materials[J].Granular Matter,2014,16(5):641-655.
[32] LI X S,DAFALIAS Y F.Anisotropic critical state theory:role of fabric[J].Journal of Engineering Mechanics,2011,138(3):263-275.
[33] XIAO Y,LIU H L,ZHU J G,et al.Dilatancy equation of rockfill material under the true triaxial stress condition[J].Science China Technological Sciences,2011,54(1):175-184.
[34] XIAO Y,LIU H,SUN Y,et al.Stress-dilatancy behaviors of coarse granular soils in three-dimensional stress space[J].Engineering Geology,2015,195:104-110.
[35] KLOSS C,GONIVA C.Liggghts-a new open source discrete element simulation software[C]//Proc.of The 5th In⁃ternational Conference on Discrete Element Methods.2010:25-26.
[36] THORNTON C,ZHANG L.On the evolution of stress and microstructure during general 3D deviatoric straining of granular media[J].Geotechnique,2010,60(5):333-341.
[37] AI J,CHEN J F,ROTTER J M,et al.Assessment of rolling resistance models in discrete element simulations[J].Powder Technology,2011,206(3):269-282.
[38] LI X S,WANG Y.Linear representation of steady-state line for sand[J].Journal of Geotechnical and Geoenvi⁃ronmental Engineering,1998,124(12):1215-1217.
[39] 郑颖人,沈珠江,龚晓南.岩土塑性力学原理[M].北京:中国建筑工业出版社,2002.
[40] BEEN K,JEFFERIES M G.A state parameter for sands[J].Géotechnique,1985,35(2):99-112.
[41] 黄茂松,曲勰,吕玺琳.基于状态相关本构模型的松砂静态液化失稳数值分析[J].岩石力学与工程学报,2014,33(7):1479-1487.
