分层型水库取水水温量纲分析及其影响因素研究

郑铁刚，刘之平，孙双科，柳海涛，牛志攀，李广宁

（1.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，北京 100038；2.四川大学 水力学与山区河流开发保护国家重点实验室，四川 成都 610065；3.中国三峡建设管理有限公司，四川 成都 610023）

1 研究背景

“水电建设开发与生态环境保护”是人与自然和谐相处中的一个重要课题，也是目前备受关注的热点问题［1］。水库温度分层是随着大规模水利水电工程兴建带来的系列生态环境问题之一，如新安江水库建成后，下游河道水温降低，影响鱼类的繁殖和生长，鲥鱼产量显著减少［2-3］。为缓解水库下泄水温对下游河道生态环境的不利影响，分层取水已经成为水电生态友好实践的重要组成部分，其主要型式分为多层取水口与叠梁门取水口结构等，目前我国的高坝电站分层取水采用叠梁门取水结构居多［4］。

鉴于分层取水对生态环境的重要性，目前国内外针对分层取水开展了大量研究，而水温结构作为影响分层取水效果的关键因素之一，更是国内外学者的研究热点，并已取得了一定的成果。如：邓云等［5］和任华堂等［6］分别采用数学模型分析了水库调度对水温结构的影响；刘兰芬等［7］采用三维数学模型对漫湾水电站水温分布进行了预测研究；Ma等［8］针对Kouris水库研究了分层取水方案对库区水温分层结构的影响；Hamblin等［9］则分析了蓄水过程对Kootenay湖水温结构的影响。此外，文献［10-12］还研究了气象条件改变对库区水温结构的影响；张士杰等［13］基于MIKE3平台，以二滩水电站为例，分析了上游来流水温与大坝出水位置对库区水温结构的影响。由此可见，不同因素对库区水温结构的影响研究目前已趋于成熟。

实施分层取水方案的聚焦点为下泄水温，但迄今为止关于下泄水温的针对性研究成果较少，且多数是结合某实际工程，研究不同取水方案下下泄水温的量值大小。高学平等［14-15］依托糯扎渡水电站工程，对叠梁门分层取水下泄水温进行了模拟预测，指出下泄水温与叠梁门高度和水库水温垂向分布有关，并根据研究结果建立了下泄水温经验估算公式；张少雄等［16］基于EFDC软件平台，对溢流式取水口下泄水温进行了数值模拟，指出取水口引水流量越大，下泄水温越高。由此可见，叠梁门分层取水下泄水温与坝前水温梯度、取水高程和取水流量等相关，然而，关于影响因素对下泄水温的影响规律及影响权重研究目前则少见报道。作者曾利用三维数学模型专门开展了下泄水温对取水高程的敏感性分析，并提出了合理的取水高程建议［17］。在此基础上，本文拟通过量纲分析法，建立下泄水温估算模型，然后结合数值计算与物理实验研究成果，采用专业统计软件，对下泄水温数据进行多元线性回归分析，提出溢流式分层取水下泄水温估算方程，基于回归结果进一步分析水温梯度、取水高程及取水流量等对下泄水温的影响规律，为实际工程应用提供参考。

2 研究方法

2.1 物理实验方法 由于水温分层效应将引起变密度流动，因此实验模型设计过程中，应遵循重力相似准则，同时保持原型与模型的密度弗劳德数相等原则，即满足：

式中：下标P和M分别表示原型和模型值；u为流速，m·s-1；g为重力加速度，m·s-2；l为长度，m；Δρ为密度差，kg·m-3；ρ为密度，kg· m-3。

将式（1）带入式（2），则式（2）可以简化为：

忽略压力对密度的影响，根据密度与温度的关系式导出温度差与密度差的关系为：

式中：T为水温，℃；ΔT为水温差，℃。分析研究表明［18］，在10～75℃范围内，系数k(T)≈-1×10-5。在本文实验过程中，供水水库的水温在15～30℃，故本文将k(T)视为常数。因此，由式（3）和式（4）导出水温相似关系：

实验系统集合供水系统、加热系统、测试系统及取水系统为一体，如图1所示。实验过程中，通过调整供水系统和加热系统，以0-0断面为监控断面，同时确定该断面为库区远区断面（原型大于取水口上游600 m范围），当断面水温分布与目标分布吻合且稳定后，开始实验数据监测。1-1断面代表取水口近区断面，距离取水口约150 m，2-2断面为取水水温断面。模型目标水温分布根据式（5）由原型目标水温分布换算得出，具体方法为：（1）按照水温分层特性，将水深划分为若干层Δhi；（2）从基底水层开始，由原型底部水温温差与模型底部水温求出该层模型温差为则该层顶部模型水温为（3）根据第二层的原型底部水温温差及该层模型底部水温求出该层顶部模型水温为（4）按照上述方法，向上逐层求解，直至水面。

由于库区水温分布发生变化，下泄水温测试结果无法直接应用于数据分析中，因此需要采取方法将下泄水温换算成原型值。考虑到水温分布对库区流态影响较小，本研究根据模型下泄水温量值对应的库区分布垂向位置，根据式（5）反算出原型水温。具体方法为：假定模型中下泄水温为TM，该值在模型水温垂线分布中的位置，介于某一层上下水温之间，即有该层上下部水温分别对应原型水温为与则原型中取水水温应为：

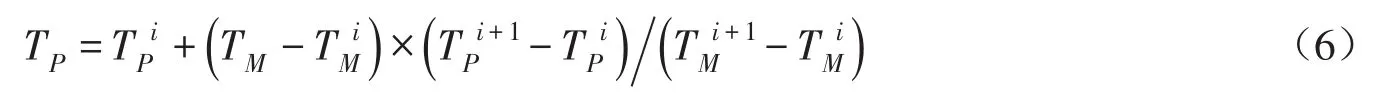
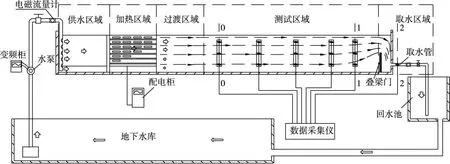
图1 水温分层试验系统简化示意

2.2 水温数学模型

2.2.1 水动力学控制方程 本文基于Boussinesq假定，采用RNGk-ε紊流模型，结合传热方程，建立了全三维取水口近区数学模型，在已知库区水温分布条件下，对下泄水温进行预测，控制方程及参数取值参考文献［17］。模型模拟库区长度为1.5 km，采用结构网格与非结构网格结合的方法，计算网格单元在主流方向上尺寸为5～30 m，在水深方向上为0.25～0.5 m，在宽度方向上为5～10 m，并在取水口近区等区域进行网格加密，网格数量为70万左右，计算时间步长为0.2 s。

2.2.2 水面热交换模型 水气界面的热交换是水体的主要热量来源，在本文已知边界条件下，起到了维持库区水温分布的作用。水面热交换包括净太阳短波辐射、净长波辐射、蒸发和传导4个方面。结合水面热交换原理，建立水面综合散热系数计算关系式为［19］：

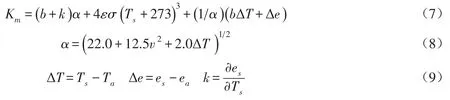
式中：α为水面蒸发系数，W·m-2·hPa-1；Km为水面综合散热系数，W·m-2·℃-1；b取为0.66P/1000，hPa·℃-1；P为水面以上1.5 m处的大气压，hPa；v为水面以上1.5 m处的风速，m/s；ε为水面辐射系数，取0.97；σ为Stefan-Boltzman常数，σ=5.67×10-8，W·m-2·℃-4；Ta为水面以上1.5 m处的气温，℃；Ts为水面水温，℃；es为水温为Ts时的相应水面饱和水汽压，hPa；ea为水面以上1.5 m处的水汽压，hPa。

2.2.3 边界及初始条件 上游设定为流速边界，y方向和z方向无速度分量，压力假设为静水压，进口边界水温分布给定固定水温分布；假定下游出口断面为充分发展的紊流，边界上各变量均取零梯度条件；初始条件库区为零流速，并给定研究工况水温分布，水面采用“刚盖假定”，库底和坝体采用无滑移边界条件，且为绝热边界。

2.3 模型验证 为验证本文物理实验与数值计算结果的准确性，本文依托某实际工程资料，选取典型工况的断面水温和流速分布及下泄水温进行验证。将库区上游1.3 km现场监测断面水温分布作为计算边界条件，选取库区上游600 m断面位置水温分布及对应尾水下泄水温进行验证，如图2所示。电站库区水温分布和发电尾水水温均为2015年6月22日和9月22日现场监测完成，由于库区水温日内变化较小，因此采用上午10时监测数据代表日内水温分布；电站尾水日内波动最大为0.5℃左右，因此本文验证采用24 h平均水温进行对比分析；库区水温传感器精度为±0.15℃，发电尾水水温传感器精度为±0.2℃。图2（a）为2015年9月22日取水口近区库区水温分布原型观测与数值模拟结果对比，图2（b）为2015年6月22日和9月22日下泄水温对比情况，对比结果显示，库区水温分布吻合较好，而发电尾水水温计算值与原型观测值误差分别为0.1℃和0.2℃，相对误差分别为0.8%和1.4%，满足研究要求。由此说明，本研究采用的数学模型可靠，研究结果可信。

由于实验工况和原型工况存在差异，因此本文结合数值计算结果对物理实验结果进行相互验证。数值计算与物理实验上游均假定一致的水温分布边界，选取取水口近区1-1断面（见图1）水温及流速分布数据进行对比，如图3所示，具体验证边界及测点说明详见参考文献［17］。由图可知，水温分布和流速分布的计算值与实验值相互吻合较好，均表现出相同的分布规律。综上所述，本文物理实验中采用的换算及模拟方法可行，研究数据可信，可以用于下泄水温的预测研究。

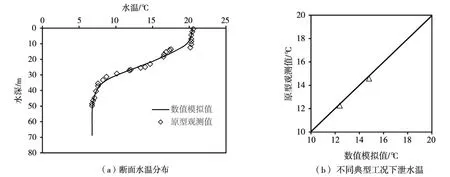
图2 数值计算结果与原型观测结果对比

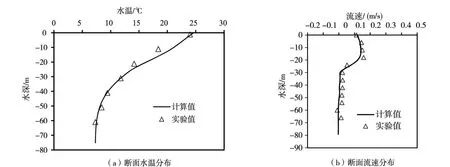
图3 物理实验与数值计算1-1断面水温、流速垂向分布对比

3 量纲分析

取水口上游的取水层厚度对分层取水下泄水温起到决定性作用。文献［20］中指出，异重流取水层的厚度与库区密度分布和取水流量有关。对于分层型水库而言，密度分布可以由水温分布代替，即分层取水下泄水温的影响因素主要可以概括为库区水温分布、取水流量和取水高程等，为研究各影响因素对下泄水温的影响程度，首先建立下泄水温估算模型。

本文假设水温分布为单温跃层分布型式，且取水范围均在温跃层范围内，则采用温跃层水温梯度来量化水库温度分层的强度，将温跃层水温分布假设为线性分布，即水库温度分层强度可以由温跃层表层水温、温跃层底层水温和温跃层厚度来表示。假设影响下泄水温的物理量有温跃层强度、温跃层厚度、取水水头、取水流量、取水口宽度和重力加速度等，则分层型水库下泄水温可以近似表示为：

式中：Tg为温度分层强度，℃/m，Ts为温跃层表层水温，℃，Tb为温跃层底层水温，℃；S为温跃层厚度，m；H为取水水头，m，等于水面高程与取水高程的差值；Q为取水流量，m3·s-1；g为重力加速度，m·s-2；B为取水口宽度，m；Tw为取水水温，℃。

将7个变量与基本量纲长度［L］、质量［M］、时间［T］和温度［θ］，建立量纲矩阵如表1所示。

表1 量纲矩阵关系

由表1可知，这些变量涉及的基本量纲为r=3，根据Buckingham提出的π定理［21］，下泄水温要求有7-3=4个独立的无量纲组π的关系式来表示。结合取水层厚度文献资料［20］，建立无量纲组为：

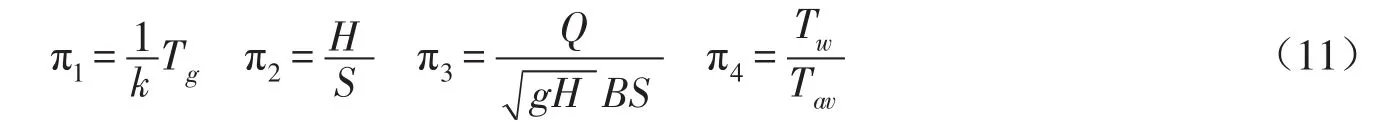
式中：Tav为温跃层平均水温，℃；k为温度分层强度修正系数，℃/m，修正温跃层分布凹状或凸状产生的影响，其取值与温跃层平均水温和厚度有关，当时，0＜k＜1，当时，k≥ 1；S为取水层厚度，m。

将温跃层内水体分成若干层，每层高度记为ds，每层水温和流速分别记为t和v，则温跃层平均温度可以表示为：

将式（11）带入方程（10），可得：

根据式（13）建立方程为：

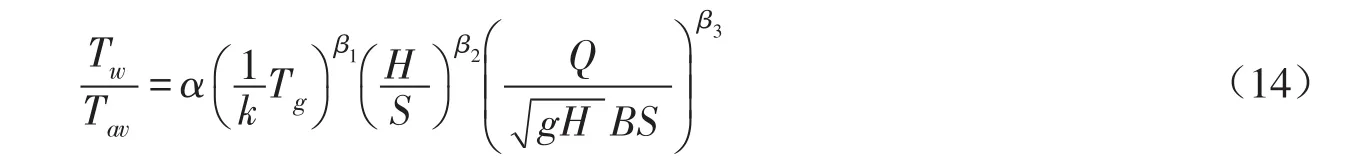
式中：α为经验系数；β1、β2和β3分别为经验指数。

4 结果与分析

4.1 基本数据资料 分层水体中，当水温分布中某一段的垂向温度梯度大于深水温度跃层的临界值时，确定该段为温跃层。以此为判断标准，将水温分布划分为若干层，逐层对水温梯度进行判断，连续满足温跃层临界值要求的合并为一个温跃层，该段的厚度为温跃层厚度S，上端和下端的水温分别记为Ts和Tb。对于温跃层的临界值，不同资料提出了不同的取值（0.05～0.2℃·m-1）［22-24］，结合本文的水温分布特点，本研究温跃层临界值取0.2℃·m-1。

前文指出，影响下泄水温的关键因子主要包括坝前水温梯度、取水水头和取水流量等。结合作者多年开展的数值计算与物理实验研究，本文共建立39组研究工况，其中取水流量为100～2 500 m3·s-1，水温分层梯度采用库区上游距坝1.5km左右断面深泓处水温垂向数据，为0.1～0.4℃·m-1，下泄水温为7～23℃，取水水头为15～25 m，温跃层厚度为40～60 m，修正系数k取1.0～1.25℃·m-1。将数值计算结果与物理实验结果归类，共计854个数据点，下文统称为实验数据，采用统计分析软件SAS 9.3对数据结果开展回归处理，并进行误差分析［25］。

表2 下泄水温多元回归分析结果

4.2 下泄水温无量纲关系研究 根据式（14），对实验数据进行多元线性回归分析，分析结果如表2所示。由表可知，回归分析结果中，每项无量纲组均达到了99%以上的显著水平。根据回归分析结果，建立下泄水温多元线性关系式为：

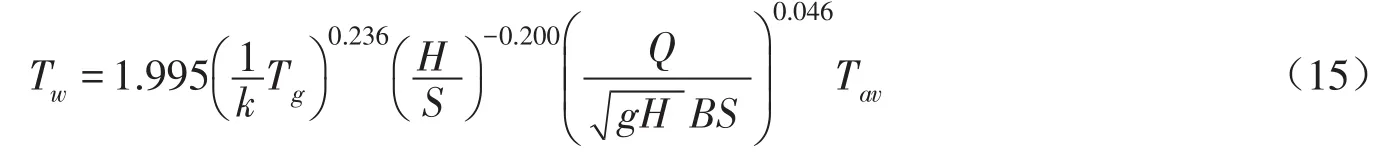
分析结果显示，温跃层强度Tgk为下泄水温计算公式的最主要影响因子，对下泄水温估算的决定系数达到81.70%，随着其它无量纲项的增加，决定系数逐渐增加，如表2所示。由表可知，下泄水温估算式中，项为第二影响因素，加上坝前水温梯度对下泄水温计算的决定系数达到88.55%。相比之下，为第三影响因素，即流量改变对下泄水温的影响相比最小。随着最后一项的增加，下泄水温估算式（15）的决定系数为91.39%。由此表明，与取水高程和取水流量相比，坝前水温梯度为影响下泄水温的最显著因素。

用单宽流量q取代Q/B项，g=9.81 m·s-2，则式（15）可以转换为：

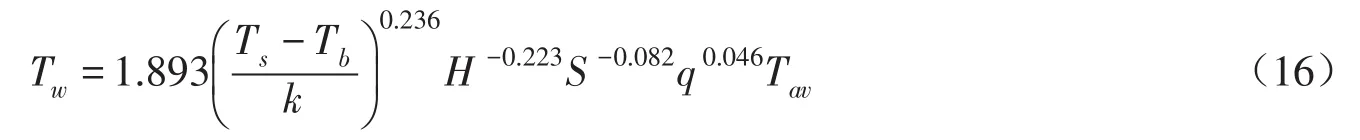
由式（16）可以看出，下泄水温与运行条件和水温分布相关，在本文研究范围内，估算模型的预测结果较为理想。图4为下泄水温公式预测结果与实验结果对比情况，由图可以看出，两者结果表现出很好的吻合性，预测数据与实验数据的相关性达到99.4%。

4.3 关键因子对下泄水温的影响研究

（1）坝前水温梯度影响。为分析坝前水温梯度对下泄水温的影响，本文选取取水水头为18.3 m工况开展研究。根据表2结果显示，Tw/Tav与（Ts-Tb）/S呈幂函数相关关系，且相关性较高。但由于Tav受Ts与Tb影响，无法直接判断下泄水温Tw和温跃层强度（Ts-Tb）/S的函数关系。为此，将实验及式（16）预测结果数据绘制于图5，由图5可知，实验水温与预测水温基本吻合，最大相对误差仅为2%；根据实验数据拟合下泄水温与坝前水温梯度关系如图5所示，下泄水温和温跃层强度呈较好的指数相关关系，拟合经验关系的决定系数R2为93.4%。当取水流量和取水高程不变时，随着坝前水温温跃层水温梯度增大，下泄水温逐渐升高，且下泄水温增幅逐渐增大。因此，根据下泄水温与坝前水温梯度拟合的单一因素经验关系表明，坝前温跃层水温梯度越大，水温梯度对下泄水温的影响越明显。

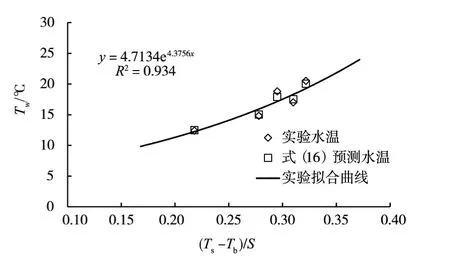
图5 下泄水温与坝前水温梯度计算公式和观测数据对比

（2）取水水头影响。根据式（16）可知，下泄水温与取水水头可近似为幂函数关系。当取水流量和坝前水温梯度不变时，下泄水温随取水水头的增加呈下降趋势，且下泄水温下降幅度明显小于取水水头的增加幅度，表2显示，取水水头项对下泄水温项的决定系数远小于坝前水温梯度项，即取水高程变化对下泄水温产生的影响明显小于坝前水温梯度变化产生的影响。

为研究单一因素条件下，取水水头对下泄水温的影响，本文选取坝前温跃层水温梯度为0.278℃/m工况进行分析，将实验与式（16）预测结果绘制于图6。由图6可知，根据实验结果，当取水水头处于某临界值时，随着取水水头的增加，下泄水温下降明显，而当取水水头从临界值逐渐减小时，下泄水温虽然处于上升趋势，但变化不再明显，下泄水温与取水水头整体表现出较好的多项式相关关系，决定系数R2达到99.77%。而本文在采用量纲分析法处理估算模型时，将下泄水温与取水水头的关系简化为幂函数相关关系，如图6预测拟合曲线，预测结果显示下泄水温随着取水水头的增加逐渐下降，且取水水头越高，下泄水温下降趋势越缓慢。虽然预测趋势与实验结果拟合曲线存在一定的误差，但对比数据可知，预测水温结果和实验水温结果最大相对误差仅3%，满足预测精度要求，且式（16）对取水水头与下泄水温关系的整体预测趋势与实验结果一致。

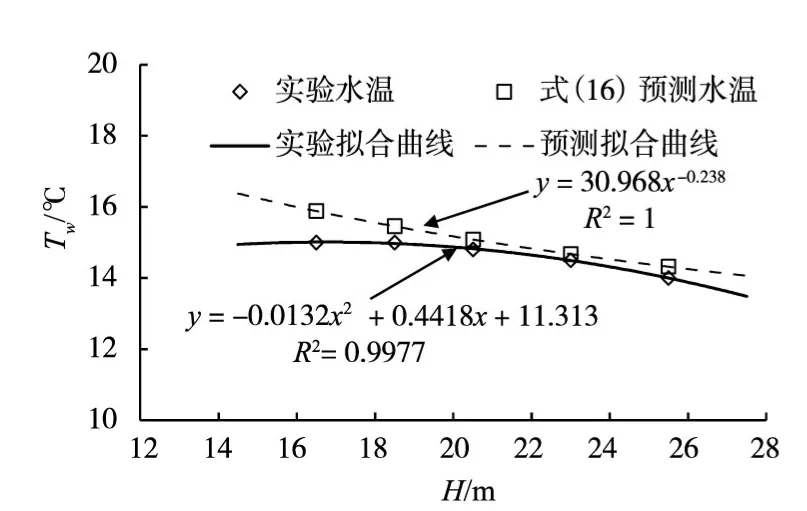
图6 下泄水温与取水水头的关系

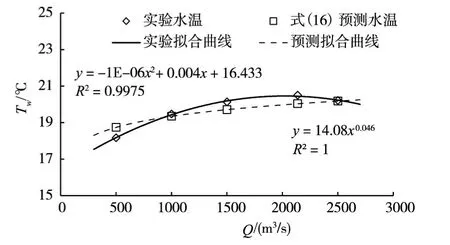
图7 下泄水温与取水流量的关系

（3）取水流量影响。由式（16）可知，单宽流量q的指数为0.046，表示随着流量的增加，下泄水温呈缓慢上升趋势，与文献［16］预测趋势相同，且采用式（16）预测文献［16］下泄水温结果，相对误差仅为2%～4%。由此表明，本文建立的式（16）预测下泄水温与流量关系具有一定的可信性。

为研究取水流量对下泄水温的影响，本文选取坝前温跃层水温梯度为0.322℃/m工况进行分析，图7为本文在多种取水流量下建立的下泄水温-取水流量关系，实验结果显示，随着取水流量的增加，下泄水温呈上升趋势，但到达某一临界值后，随着取水流量的增加，下泄水温又呈下降趋势，下泄水温与取水流量呈很好的二次多项式关系，决定系数达到99.75%。分析其原因，当取水流量较小时，叠梁门顶流速较小，叠梁门顶热通量较小，随着取水流量的增大，热通量逐渐增大，下泄水温升高；当取水流量大于某临界值时，取水层厚度明显增大，温跃层内下部低温水被提取，从而导致下泄水温降低。本文在水温预测模型建立时，将下泄水温与取水流量关系假定为幂函数关系，预测曲线与实验曲线产生了一定的误差，但误差分析发现，研究范围内最大相对误差仅为2.5%，最小为0.5%，可以满足下泄水温估算要求。

5 结论与讨论

影响溢流式分层取水下泄水温的因素有：温跃层强度、温跃层厚度、取水水头、取水流量、取水口宽度和重力加速度等。本文采用量纲分析法，尝试建立了下泄水温估算模型，并采用SAS 9.3统计分析软件对实验数据进行了多元线性回归分析，估算方程与实验数据的决定系数达到91.39%，由此表明本文建立的估算方程可以用于下泄水温估算。在本文研究工况范围内，通过单因素影响分析可知，当取水流量和取水高程不变时，随着坝前水温温跃层水温梯度增大，下泄水温升高，且水温梯度越大，对下泄水温的影响越显著；当取水流量和坝前水温梯度不变时，下泄水温随取水水头的增加而降低，下泄水温降低幅度明显小于取水水温变幅；当取水流量单因素改变时，随着取水流量的增大，下泄水温逐渐升高，但取水流量大于临界值时，下泄水温转而表现出缓慢下降趋势。总体分析表明，坝前水温梯度对下泄水温的影响最为显著，其次为取水高程，最后为单宽流量。

在本文考虑变量的研究范围内，估算模型同样适用于其他水库，只要已知库区水温分布、取水高程和取水流量等参数，均可采用模型估算该取水条件下的取水水温，如采用模型估算文献［16］中水库下泄水温相对误差仅为2%～4%。虽然本文建立了相关性很好的下泄水温无量纲估算式，但由于本文数据范围有限，并缺乏原型观测数据资料，导致方程（16）尚具有一定的局限性，式中各项的指数β需进一步修正，进而调整各影响因素对下泄水温估算的影响程度，估算模型适用范围目前仅限于本文参数所在研究范围。此外，本研究将取水高程及取水流量的影响简化为幂函数相关，尽管预测结果与实验结果产生了一定误差，但整体预测结果与实验结果相关系数达0.994，可以满足估算需求。为进一步提高下泄水温估算精度及适用性，下一步将对下泄水温的关键因子影响规律开展深入研究，结合原型观测数据等，补充样本数量，拓展模型应用范围。

参 考 文 献：

［1］ 董哲仁，孙东亚，赵进勇，等.生态水工学进展与展望［J］.水利学报，2014，45（12）：1419-1426.

［2］ 段文刚，王才欢，杜兰，等.大型分层取水电站进口水力学研究进展［J］.长江科学院院报，2013，30（8）：5-9.

［3］ 李倩，李翀，骆辉煌.长江上游珍稀、特有鱼类生态水温目标研究［J］.中国水利水电科学研究院学报，2012 ，10（2）：86-91.

［4］ 傅菁菁，李嘉，芮建良，等.叠梁门分层取水对下泄水温的改善效果［J］.天津大学学报：自然科学与工程技术版，2014，47（7）：589-595.

［5］ 邓云，李嘉，李然，等.水库调度对溪洛渡电站下游水温的影响［J］.四川大学学报：工程科学版，2006，38（5）：65-69.

［6］ 任华堂，陶亚，夏建新.不同取水口高程对阿海水库水温分布的影响［J］.应用基础与工程科学学报，2010，18（S1）：84-91.

［7］ 刘兰芬，张士杰，刘畅，等.漫湾水电站水库水温分布观测与数学模型计算研究［J］.中国水利水电科学研究院学报，2007，5（2）：87-94.

［8］ MA S，KASSINOS S，KASSINOS D，et al.Effects of selective water withdrawal schemes on thermal stratification in Kouris Dam in Cyprus［J］.Lake&Reservoirs：Research and Management，2008，13：51-61.

［9］ HAMBLIN P F，McADAM S O.Impoundment effects on the thermal regimes of Kootenay Lake，the Arrow Lakes Reservoir and Upper Columbia River［J］.Hydrobiologia，2003，504（1）：3-19.

［10］ JOHNSON B M，SAITO L，ANDERSON M A，et al.Effects of climate and dam operations on reservoir thermal structure［J］.Journal of Water Resources Planning and Management，2004，130（2）：112-122.

［11］ MAHSA M，AMIR E，EBRAHIM J.Effects of climate change on the thermal regime of a reservoir［J］.Proceed⁃ings of the Institution of Civil Engineers-Water Management，2014，167（10）：601-611.

［12］ 孙昕，王雪，许岩，等.一个分层水库温跃层的模拟与验证［J］.湖泊科学，2015，27（2）：319-326.

［13］ 张士杰，彭文启.二滩水库水温结构及其影响因素研究［J］.水利学报，2009，40（10）：1254-1258.

［14］ 高学平，张少雄，张晨.糯扎渡水电站多层进水口下泄水温三维数值模拟［J］.水力发电学报，2012，31（1）：195-201.

［15］ 高学平，陈弘，宋慧芳.水电站叠梁门多层取水下泄水温公式［J］.中国工程科学，2011，13（12）：63-67.

［16］ 张少雄，高学平.水库溢流式取水口下泄水温数值模拟［J］.应用基础与工程科学学报，2015，23（1）：145-153.

［17］ 郑铁刚，孙双科，柳海涛，等.大型分层型水库下泄水温对取水高程敏感性分析研究［J］.水利学报，2015，46（6）：714-731.

［18］ 柳海涛，孙双科，王晓松，等.大型深水库分层取水水温模型试验研究［J］.水力发电学报，2012，31（1）：129-134.

［19］ GB/T 50102-2003，工业循环水冷却设计规范［S］.

［20］ 范家骅.异重流运动的试验研究［J］.水利学报，1959（5）：30-48.

［21］ 李家星，赵振兴.水力学［M］.南京：河海大学出版社，2001.

［22］ 王银珠，濮培民.抚仙湖水温跃层的初步研究［J］.海洋湖沼通报，1982（4）：1-9.

［23］ 国家海洋局.海洋调查规范海洋调查资料处理［S］.北京：海洋出版社，1992.

［24］ SPRINTALL J，TOMCZAK M.Evidence of the barrier layer in the surface layer of the tropics［J］.Journal of Geo⁃physical Research，1992，97（C5）：7305-7316.

［25］ SAS.SAS/STAT 9.3 User’s Guide［M］.Cary，NC：SAS Institute Inc.，2011.