基于Voronoi细观数值模型预测PBX的有效弹性模量

王竟成, 罗景润

(中国工程物理研究院总体工程研究所, 四川 绵阳 621999)

1 引 言

高聚物粘结炸药(Polymer Bonded Explosive, PBX)是一种颗粒高度填充复合材料,具有复杂的微细观结构。颗粒的性能、形貌、尺寸分布以及粘结剂的性质都对PBX的宏观性能有着密切的影响。细观力学逐渐发展了多种理论方法预测复合材料的有效性能[2-3],如上下界限法、稀疏法、Mori-Tanaka法、自洽法、微分法等,这些方法应用于PBX存在以下问题:

(1)PBX的颗粒含量很高,而传统细观力学方法预测颗粒含量较高的复合材料有效性能会出现很大偏差;

(2)PBX组分中颗粒与基体的弹性模量相差3～4个数量级,以致这些方法预测的结果具有量级上的差异;

(3)PBX炸药颗粒是典型的不规则多面体,而细观理论方法通常假设夹杂颗粒为球形或椭球形,难以很好地刻画PBX的细观结构特征。

由于上述细观力学理论方法的局限性,构建合适的细观数值模型,采用有限元法计算PBX的有效性能是一种有效途径。目前,PBX的细观数值模型主要有: 圆形颗粒规则排布和随机排布[6-9]、六边形颗粒规则排布、正方形颗粒模型。基于这些模型,采用有限元方法,可以实现对PBX有效性能的预测,但是,这些数值模型并未反映PBX炸药颗粒的不规则多面体特征,其预测结果与实测值差异较大。本研究采用Voronoi法以种子点为中心生成随机多边形颗粒,颗粒的平均尺寸通过种子数进行控制,建立了Voronoi细观数值模型,力图较真实反映PBX细观颗粒特征,实现炸药颗粒的高度填充。

2 数值模拟

2.1 细观模型的建立

为考察颗粒形貌和排列分布方式对PBX有效模量的影响,首先建立四种构型的二维RVE模型: circle_r(图1a)为圆形颗粒随机排布模型,circle_1(图1b)为圆形颗粒规则排布模型1,circle_2(图1c)为圆形颗粒规则排布模型2,hexagon(图1d)为六边形颗粒规则排布模型。其中,图1a,图1b,图1c为圆形颗粒的不同分布形式,颗粒含量均为49%,用于分析颗粒排列分布对有效模量的影响; 图1d与图1c的颗粒含量、分布形式相同,用于分析颗粒形貌的影响。

图2a为超声波下PBX的细观形貌: 炸药颗粒为不规则多面体,含量极高。为接近PBX的细观形貌,实现炸药颗粒的高度填充,更有效地模拟PBX的有效力学性能,建立不规则多边形颗粒的Voronoi模型。在一定区域内播撒随机种子点,采用Voronoi法[10]以种子点为中心生成随机多边形颗粒。颗粒的平均尺寸通过种子数进行控制。为保证颗粒生成的形态质量,有必要筛选种子点。图2b为具有周期性结构的Voronoi图,炸药颗粒的平均粒径为100 μm。进一步生成粘结剂层后,将节点信息导入ANSYS获得有限元模型(图2c),它与PBX真实的细观形貌(图2a)具有较好的相似性。将种子点固定,改变粘结剂的厚度构建不同颗粒含量的Voronoi模型,其颗粒形貌和分布形式完全相同,有利于研究颗粒含量对PBX有效性能的影响。

a. circle_rb. circle_1c. circle_2d. hexagon

图1不同排布或形貌的代表性体积单元(RVE)模型

Fig.1RVE models with different particle distributions or shapes

a. digital image[11]b. Voronoi imagec. Voronoi model

图2超声波下PBX细观形貌和Voronoi模型

Fig.2Digital image under ultrasonic and Voronoi model for PBX

计算中炸药颗粒选用奥克托今(HMX)晶体,粘结剂选用聚酯型聚氨酯(Estane),均采用各向同性的弹性本构模型,其理想材料参数见表1[12]。从表1中可见基体Estane和炸药颗粒HMX之间的弹性性能有巨大的差异,泊松比相差一倍,杨氏模量相差四个数量级。

表1各组分弹性参量

Table1The elastic properties of ingredients

ingredientE/MPaνmatrix：Estane0．770．499particles：HMX2．5325×1040．25

Note:Eis the Young′s modulus,νis the Poisson′s ratio.

2.2 RVE尺寸的选择

代表性体积单元(Representative Volume Element, RVE)是细观力学中的一个基本概念,需要满足尺度的二重性: 宏观上可以看成一个物质点,RVE中的宏观应力、应变场可视为均匀的; 细观上包含了足量的细观结构信息,可以代表局部连续介质的统计平均。细观应力应变场只通过它们的体积平均值对材料的宏观性能产生影响[13]。不同材料选取的RVE尺寸有很大的差别,一般来说需要满足:Lc≪LRVE≪LM,Lc为材料组分特征尺寸,LRVE为RVE尺寸,LM为结构宏观特征尺寸。只有当LRVE/Lc足够大时,非均匀材料组分结构的统计平均性质才能趋于稳定,细观结构的不确定影响才能忽略不计。

适当尺寸的RVE,其有效弹性性质不受边界条件类型的影响[14-15]。Lemaitre[16]曾对各种典型材料代表性单元的最小尺寸进行了粗略估计,金属: 0.1 mm×0.1 mm×0.1 mm,混凝土: 100 mm×100 mm×100 mm,木材: 10 mm×10 mm×10 mm,高分子和颗粒复合材料: 1 mm×1 mm×1 mm。Ostoja-Starzewski[17]研究片状或针状颗粒复合材料的有效刚度后发现,在最大许可误差为5%和颗粒刚度是基体刚度100倍的情况下,RVE最小尺寸是颗粒特征尺寸的10～20倍。真实炸药颗粒的平均尺寸约100 μm,因此选择PBX二维RVE模型的尺寸为1000 μm×1000 μm。

2.3 有限元计算方法

采用周期性的RVE模型(图3)来模拟均匀化介质的力学行为,平行于边界面的边界节点位移通过以下关系耦合起来:

ui-uj=0

(1)

式中，ui,uj分别为边界节点i和j平行于边界面的位移,μm。采用易于实现的均匀应变边界条件进行有效模量的计算,即左边界和下边界分别约束住x和y向位移,上边界和右边界进行耦合约束,上边界通过施加位移载荷来模拟单轴压缩试验,见图4。有限元模拟采用平面应变假设和平面八节点单元plane183。

图3周期性的Voronoi模型

Fig.3Periodic Voronoi models

图4边界条件

Fig.4Boundary conditions

根据平面应变假设和边界条件,由:

(2)

可得:

(3)

(4)

式中,Ux为右边界节点x向位移,μm;Uy为上边界节点y向位移,μm。

根据文献[18],平均应力既可以使用体积分得到,也可以通过面积分得到:

(5)

式中，F代表作用反力,N为RVE边界上节点的个数。对于当前二维问题,可简化为:

(6)

式中，Fre为ANSYS后处理中提取的上边界节点反力之和,N。利用式(3)、(4)、(6)有:

(7)

进一步求解出体积模量K和剪切模量G:

(8)

式中,Uy为采用均匀应变边界条件时,在上边界节点施加的位移载荷,μm;Ux为后处理中提取的右边界节点位移Ux,μm;Fre为上边界节点反力之和,N;ν为泊松比,E为杨氏模量,Pa;K为体积模量,Pa;G为剪切模量,Pa。

3 结果与讨论

表2列举了圆形颗粒不同分布形式之间的有限元结果,用于分析颗粒分布形式对有效模量的影响。circle_r与circle_1各项差异都较小; 在相同颗粒含量下,不同分布形式之间泊松比ν和体积模量K的变化相对较小,而杨氏模量E和剪切模量G的差异却较大,说明E和G对颗粒分布形式更为敏感。以circle_2为标准,c=49%时,circle_1中E高出76.97%,G高出78.22%;c=64%时,E和G分别高出158.96%和160.56%。可见,这两种排布方式随着颗粒含量的增加,差异在进一步增大。以上分析说明,颗粒的排布方式对PBX的有效模量有显著影响,且其影响随着颗粒含量的上升有增大的趋势; 颗粒含量很高时,使用炸药颗粒规则排布的简单模型可能引起PBX有效性能预测的极大偏差; 因此,在构建细观模型时应当考虑炸药颗粒空间分布特征。

表2不同分布形式的有限元结果

Table2Finite element results of different particle distributions

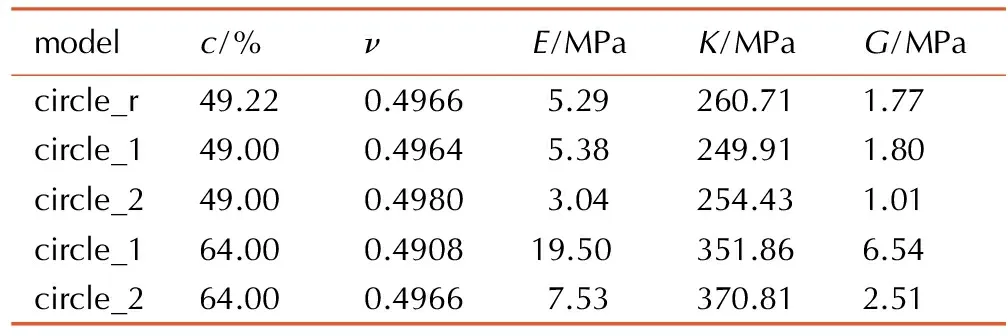
modelc/%νE/MPaK/MPaG/MPacircle＿r49．220．49665．29260．711．77circle＿149．000．49645．38249．911．80circle＿249．000．49803．04254．431．01circle＿164．000．490819．50351．866．54circle＿264．000．49667．53370．812．51

Note:νis the Poisson′s ratio;Eis the Young′s modulus;Kis the bulk modulus;Gis the shear modulus;cis content.

图1c(圆形颗粒circle_2)和图1d(六边形颗粒)拥有完全相同的排布形式,颗粒尺寸也大小相当,用于分析颗粒形貌对PBX有效模量的影响。有限元结果见表3,从表3中可以看出不同颗粒形貌间ν和K的偏差均低于2%,E和G对颗粒形貌也更为敏感; 以circle_2为标准,三种颗粒含量下,六边形颗粒的杨氏模量E分别高出36.18%,114.08%,125.48%,剪切模量G分别高出36.63%,115.14%,126.53%。随着颗粒含量的增加,颗粒形貌对有效模量的影响在逐渐增大; 颗粒含量很高时,粗略地将颗粒近似为圆形或六边形也会给有效模量的预测结果带来较大的偏差; 因此,构建细观模型时有必要更精准地刻画PBX的颗粒形貌,而Voronoi模型提供了一种较好的方法。

表3不同颗粒形貌的有限元结果

Table3Finite element results of different particle shapes

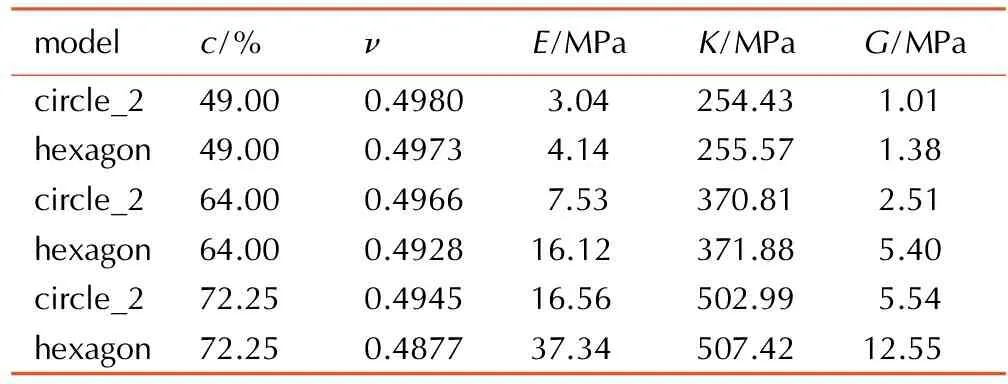
modelc/%νE/MPaK/MPaG/MPacircle＿249．000．49803．04254．431．01hexagon49．000．49734．14255．571．38circle＿264．000．49667．53370．812．51hexagon64．000．492816．12371．885．40circle＿272．250．494516．56502．995．54hexagon72．250．487737．34507．4212．55

PBX颗粒含量约90%,颗粒的分布形式和形貌对有效模量的影响非常大。因此与PBX真实细观形貌更接近的Voronoi模型能更好地预测其有效模量。此外,Voronoi模型能够实现炸药颗粒的超高填充度,这是圆形颗粒很难满足的。表4列举了颗粒含量为49%～94.9%的Voronoi模型有效模量的有限元结果。随着颗粒含量的增加,泊松比不断减小,E、K、G均迅速增大。c=94.9%时有限元结果E=1.410 GPa,而准静态下相同含量PBX杨氏模量实验值为(1.015±0.11) GPa[19]。有限元计算中使用理想的材料参数,炸药晶体与粘结剂之间的界面处理为共节点的完美粘接。而实际上组分材料内部存在众多微裂纹、微孔洞等细观损伤形式,组分界面间也存在各种缺陷,这都对PBX有效性能有弱化作用,因此有限元结果较实验值偏大。此外,目前有限元模型中未考虑颗粒粒径的分布,这可能也是造成差异的原因。

表4不同颗粒含量下Voronoi模型的有限元结果

Table4Finite element results of Voronoi models with different particle contents

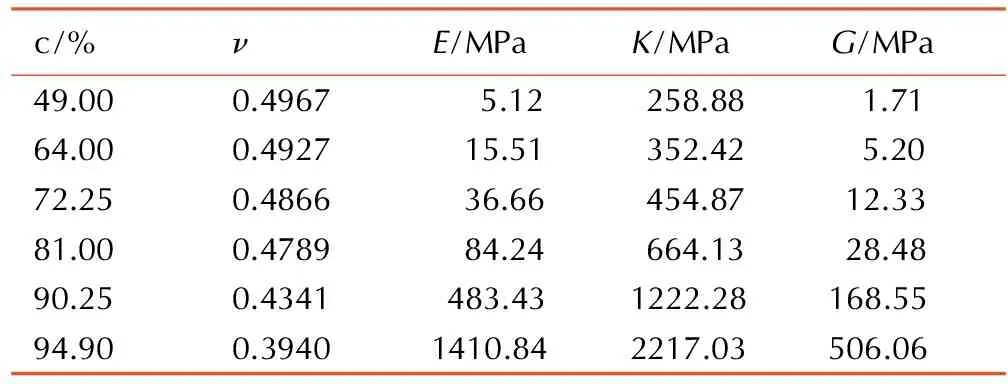
c/%νE/MPaK/MPaG/MPa49．000．49675．12258．881．7164．000．492715．51352．425．2072．250．486636．66454．8712．3381．000．478984．24664．1328．4890．250．4341483．431222．28168．5594．900．39401410．842217．03506．06

图5展示了不同颗粒含量下Voronoi模型计算结果的变化趋势,同时给出了circle_2模型、hexagon模型的计算结果作为对比。由于组分Estane与HMX的模量相差巨大,颗粒含量对有效模量的影响十分明显。泊松比ν随颗粒含量的增加快速下降(图5a),杨氏模量E(图5b)、体积模量K(图5c)、剪切模量G(图5d)三者随颗粒含量的增加近似指数上升。各模型之间体积模量差异相对最小。颗粒含量低于75%时,hexagon模型与Voronoi模型计算结果较为一致; 颗粒含量高于75%时,两者出现明显差异,hexagon模量更明显地高估了PBX的有效模量。

a. Poisson′s ratio

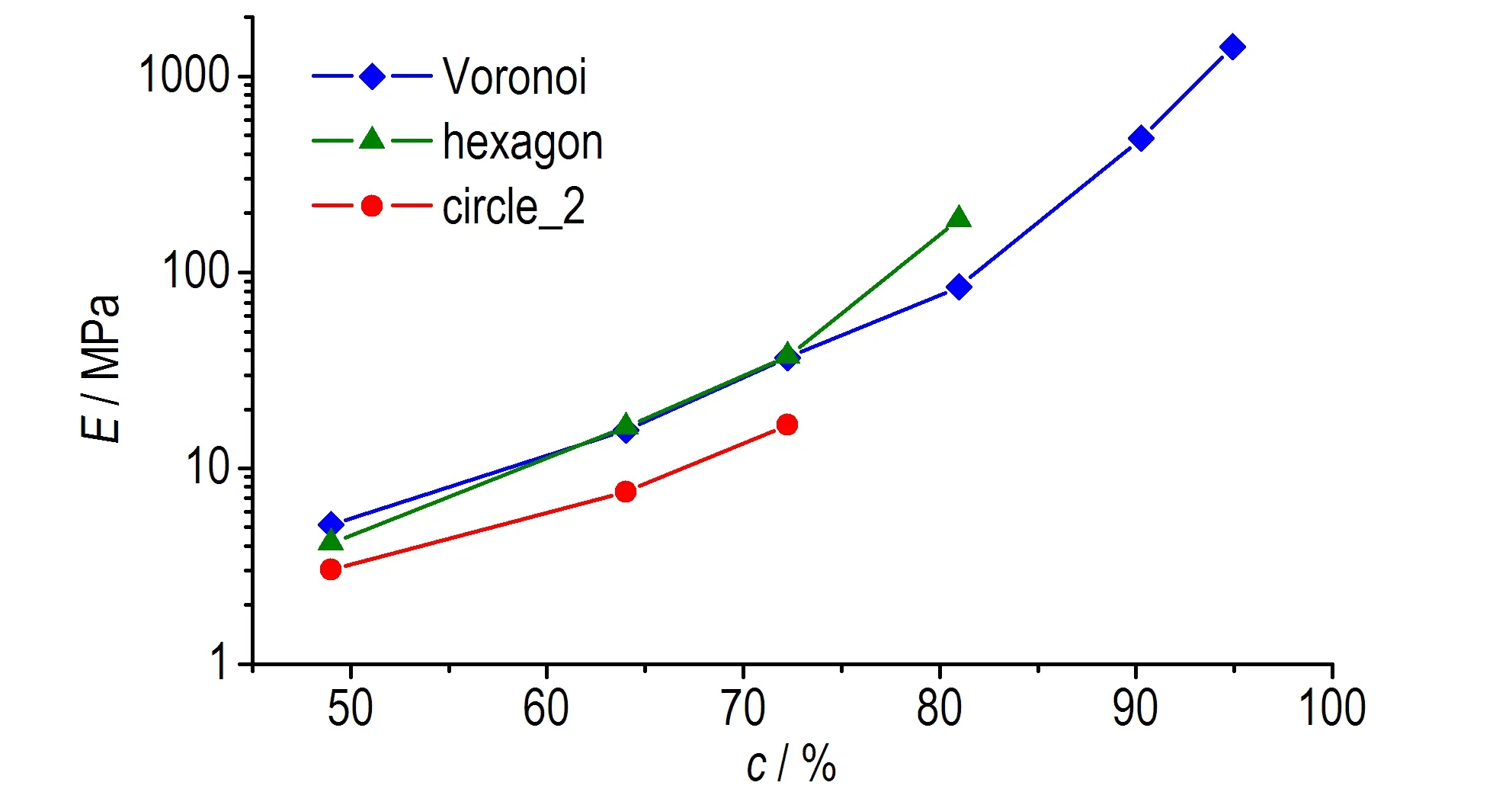
b. Young′s modulus

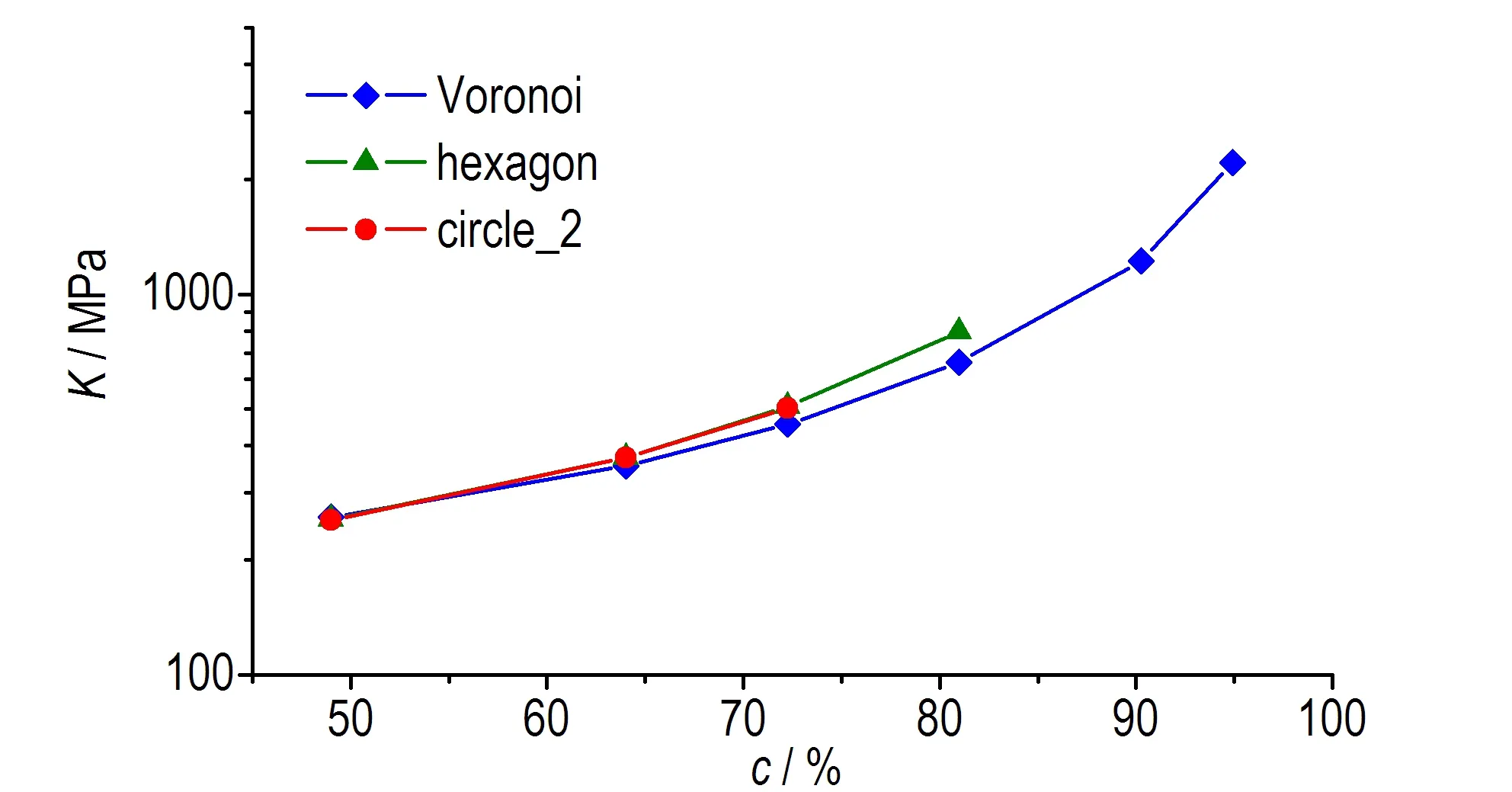
c. bulk modulus

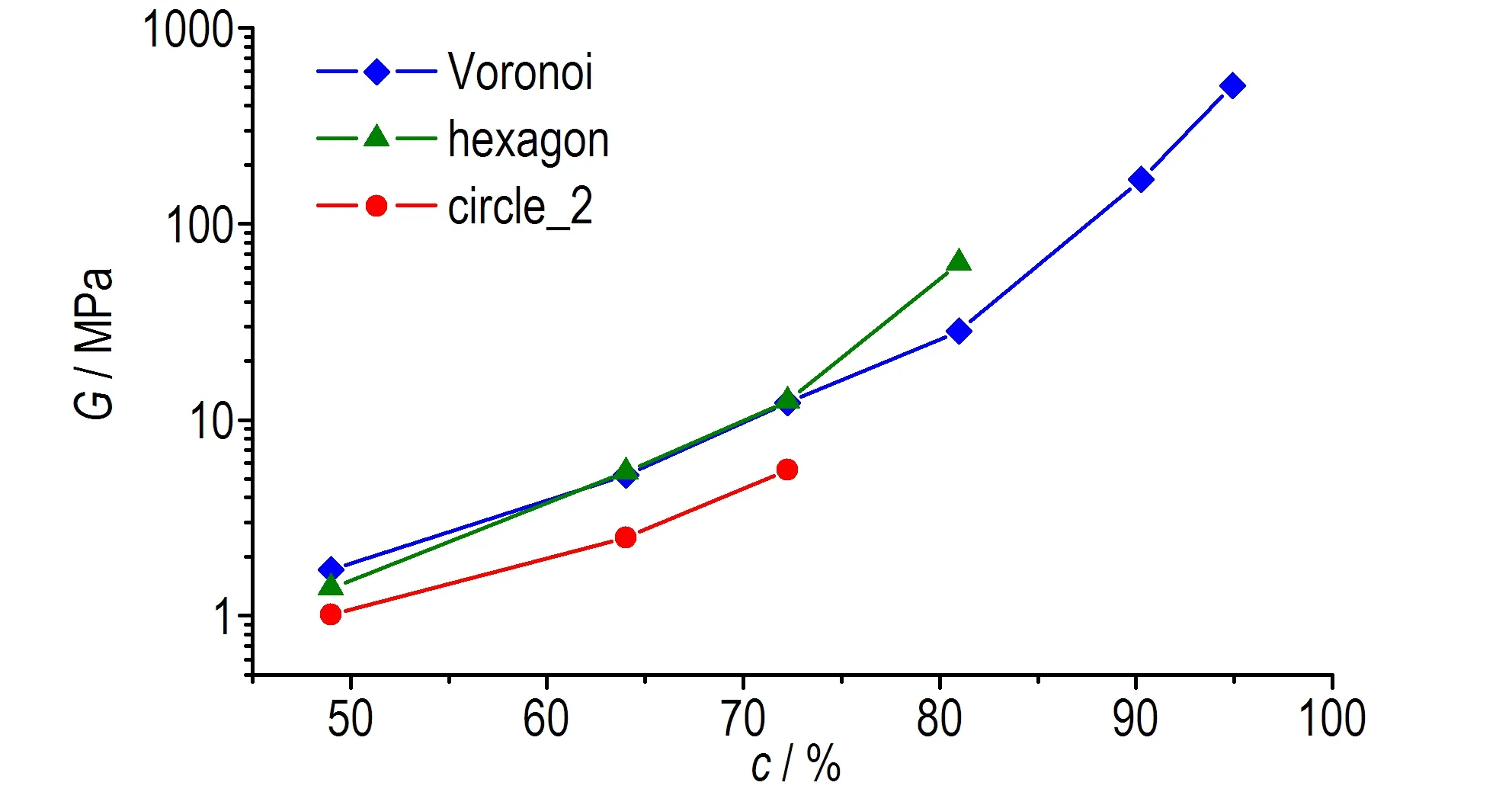
d. shear modulus

图5各模型有效性能计算结果对比

Fig.5Comparison of the effective property results calculated by different models

4 结 论

(1) 由于PBX颗粒含量极高,组分弹性模量相差3～4个数量级,杨氏模量和剪切模量对炸药颗粒的分布形式和形貌都很敏感。

(2) 以随机种子点为中心,采用Voronoi法生成随机多边形颗粒,建立Voronoi细观数值模型,既较真实地反映了PBX的细观颗粒特征,又实现了炸药颗粒的高度填充,其杨氏模量预测结果与实测值比较接近。

(3) 基于Voronoi模型的结果表明,PBX的杨氏模量、体积模量、剪切模量均随着颗粒含量的增加近似指数上升,而泊松比随颗粒含量的增加快速下降。

参考文献:

[1] 罗景润. PBX的损伤、断裂及本构关系研究. 绵阳: 中国工程物理研究院, 2001.

LUO Jing-run. Study on damage, fracture and constitutive relation of PBX. Mianyang: China Academy of Engineering Physics, 2001.

[2] 黄克智, 黄永刚. 固体本构关系. 北京: 清华大学出版社, 1999: 120-172.

HUANG Ke-zhi, HUANG Yong-gang. Solid constitutive relations. Beijing: Tsinghua University Press, 1999: 120-172.

[3] 胡更开, 郑泉水, 黄筑平. 复合材料有效弹性性质分析方法. 力学进展, 2001, 31(3): 361-393.

HU Geng-kai, ZHEN Quan-shui, HUANG Zhu-ping. Micromechanics methods for effective elastic properties of composite materials.AdvancesinMechanics, 2001, 31(3): 361-393.

[4] 敬仕明, 李明, 龙新平. PBX有效弹性性能研究进展. 含能材料, 2009, 17(1): 119-124.

JING Shi-ming, LI Ming, LONG Xin-ping. Progress in predicting the effective elastic properties of PBX.ChineseJournalofEnergeticMaterials(HannengCailiao), 2009, 17(1): 119-124.

[5] Rae P J, Goldrein H T, Palmer S J, et al. Quasi-static studies of the deformation and failure ofβ-HMX based polymer bonded explosives.MathematicalPhysical&EngineeringSciences, 2002, 458: 743-762.

[6] Annapragada S R, Sun D W, Garimella S V. Prediction of effective thermo-mechanical properties of particulate composites.ComputationalMaterialsScience, 2007, 40: 255-266.

[7] 贾宪振, 王浩, 王建灵. 炸药有效弹性性能的细观尺度仿真预估. 含能材料, 2013, 21(4): 469-472.

JIA Xian-zhen, WANG Hao, WANG Jian-ling. Mesoscale simulation of effective elastic properties of explosive.ChineseJournalofEnergeticMaterials(HannengCailiao), 2013, 21(4): 469-472.

[8] 戴开达, 刘龑龙, 陈鹏万. PBX炸药有效弹性模量的有限元模拟. 北京理工大学学报, 2012, 32(11): 1154-1158.

DAI Kai-da, LIU Yan-long, CHEN Peng-wan. Finite element simulation on effective elastic modulus of PBX explosives.TransactionsofBeijingInstituteofTechnology, 2012, 32(11): 1154-1158.

[9] Biswajit B. Effective elastic moduli of PBX from finite element simulations[EB/OL]. arXiv: cond-mat/0510367.

[10] 孙继忠, 胡艳, 马永强. 基于Delaunay三角剖分生成Voronoi图算法. 计算机应用, 2010, 30(1): 75-77.

SUN Ji-zhong, HUYan, MA Yong-qiang. Voronoi diagram generation algorithm based on Delaunay triangulation.JournalofComputerApplication, 2010, 30(1): 75-77.

[11] CHEN Peng-wan, HUANG Feng-lei, DING Yan-sheng. Microstructure, deformation and failure of polymer bonded explosives.JournalofMaterialsScience, 2007, 42: 5272-5280.

[12] Ananda B, Zhou M. A lagrangian framework for analyzing microstructure level response of polymer-bonded explosives.ModelingandSimulationinMaterialsScienceandEngineer, 2011, 19: 1-24.

[13] 张妍, 韩林. 细观力学基础. 北京: 科学出版社, 2014: 4-7.

ZHANG Yan, HAN Lin, Foundation of mesomechanics. Beijing: Science Press, 2014: 4-7.

[14] Kanit T, Forest S, Galliet I, et al. Determination of the size of the representative volume element for random composites statistical and numerical approach.InternationalJournalofSolidsandStructure, 2003, 40: 3647-3679.

[15] Sab K. On the homogenization and the simulation of random materials.EuropeanJournalofMechanicsSolids, 1992, 11: 585-607.

[16] Lemaitre J. Formulation and identification of damage kinetic constitutive equations.ContinuumDamageMechanicsTheoryandApplications, 1987, 295: 37-89.

[17] Ostoja S M. Random field models of heterogeneous materials.SolidsandStructures, 1998, 35: 2429-2455.

[18] Nguyen V D, Bechet E, Geuzaine C, et al. Imposing periodic boundary condition on arbitrary meshes by polynomial interpolation.ComputationalMaterialScience, 2012, 55(5): 390-406.

[19] Gray G T, Idar D J, et al. High- and low-strain rate compression properties of several energetic materail composites as a function of strain rate and temperature∥11thinternational detonation symposium, Snowmass, Colorado, 1998.