智性抽象概念 提升思维素养
——“分数的初步认识”教学实录与思考
2017-05-07
【本文系江苏省教育科学“十三五”规划课题“旨在核心素养提升的小学数学‘智性学习’理论与实践研究”(批准号:D/2016/02/77)的研究成果之一。】
一、重构历史情境,再创造分数
师:小朋友们,喜欢听故事吗?今天的数学课上老师就和大家一起编故事,学数学。
(画外音:古时候,有一个人只会打猎,有一个人只会捕鱼……)
师:今天老师来表演故事中的猎人,那你们表演——
生:故事中的渔夫。
师:哎,打猎打猎,天天吃肉,多腻呀。
生:哎,捕鱼捕鱼,天天吃鱼,一点儿也不想吃鱼了。
师:我好想吃鱼哦。
生:我好想吃肉啊。要不咱们就——换着吃。
师:那怎么换呢?
(课件出示图1:两条鱼换一块肉)
图1
师:有一天,捕鱼的拿4条鱼来换,他能换我几块肉呢?
生:4条鱼换2块肉。
(画外音:这样打猎的天天有鱼吃,捕鱼的天天有肉吃,日子过得无比幸福。直到有一天,捕鱼的只抓到一条鱼。捕鱼的犯愁了:两条鱼换一块肉,我会呀。今天只有一条鱼,怎么换呢)
生:一条鱼可以换半块肉。
师:半块(很吃惊的样子),还能用这些自然数表示吗?(指着 1、2、4)看来,过去学过的自然数在这里不管用了,1都嫌大了,我们要创造一种新的数来表示半块肉。那怎么得到半块肉?
生:切一半。
师:看来得把这块肉分一分,捕鱼的看仔细了,(很得意的样子)我开始分了,把半块肉拿去吧。(如图 2)

图2
生:不对,这半块太小了。
师:不对吗?(故作惊讶)我切的就是半块呀,你看!是你们没说清楚,再给你们一次机会,请说清楚让我怎么分。
生:应该从最中间切开。
师:从最中间切开意味着什么?
生:平均分。
师:平均分,我会呀。捕鱼的,看仔细,我开始分了,来,拿去吧。(如图 3)
(沾沾自喜的样子)

图3
生:不对,不对。
师:怎么又不对了?看来光说平均分还不行,那你们得给我说清楚,到底怎么平均分。
生:平均分,分成2份。
师:你要几份?
生:要1份。
师:谁能把这种分法完整地说一下?
生:把一块肉平均分,分成2份,要1份。
师:哦,这样说我就会分了。看清楚,是不是这样分?(如图4)谁来总结一下,怎样分出半块肉才符合我们的公平交换协议?

图4
教学思考:从整数到分数是数的概念的一次扩展,无论在意义上还是在读写上,分数和整数都有很大的差别。从数学发展史的角度来看,分数是在度量、分物时不能正好得到整数结果的背景下产生的。怎样让孩子在数学情境中,自然萌发出当用“1”表示都嫌大时,需要一种新的数来表示的需求呢?学生的知识经验里有“平均分”的认识,如“把1块肉平均分成2份”,学生知道每份是“半块”。但学生的经验具有原始、肤浅、片面、模糊等特点,不同的学生对“半个”的理解有不同的含义,如“大半个”“小半个”“半个”。怎样把错误的、模糊的经验转化为正确的、清晰的经验,再基于正确的经验建构数学概念?为此,老师创设了以鱼换肉的故事情境,和孩子分别扮演猎人和渔夫,在充满悬念的故事情境中,学生不知不觉进入自己的“课堂角色”,在寓教于乐的轻松氛围中,巧妙地将一个规定性数学概念转化为一个探索性的数学问题。故事情节层层递进,娓娓道来,在不断调整中,学生逐步明晰确定一个分数,必须把握住三个要点:平均分、分成几份、取几份。这三个要点紧密联系,缺一不可,把握住了分数的三个要点,也就抓住了分数的本质,建构了分数模型。
二、立足思维提升,紧扣本质建构模型
师:第二天,捕鱼的又抓到了一条鱼,谁来说说我的肉怎么换给他?
(生:答略)
师:第三天,又捕到了一条鱼,怎么换我的肉?
(生:答略)
师:看来要说清楚半块肉,得说清哪几件事?
生:要说清楚半块肉,就要说清三件事:平均分、分成 2份、拿1份。
师:每次都要说清楚三件事,有什么感觉?
生:换半块肉,要说清楚三点,觉得很麻烦。
师:你们捕鱼的,天天吃鱼,一定比我聪明,那能不能创造一种新的写法(画法)表示出这三个要点?自己动手在作业纸上写一写、画一画,然后在小组里交流一下。
(生汇报。如图 5)
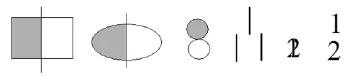
图5
师:哇,这么多表示的方法!捕鱼的,凡是能表达清楚三个要点的,都是可行的。数学的表达本身是很自由的,同时数学又是追求简洁的,现在数学上是这样规定的:先写短横(表示平均分),然后写分成的份数(写分母2),再写拿走的份数(写分子1)。这就是我们今天创造的第一个新的数,读作:二分之一。
师:现在谁来告诉我一条鱼能换几块肉?
师:用一个数就把我们要表达的三件事都说清楚了,看看数学多简洁!分肉分出了新的数,生活中哪儿还有呢?
……
(生汇报。如图6)
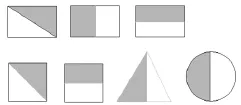
图6
生:这没有什么奇怪的,就像数1,既可以表示1张课桌,又可以表示1本书、1个小朋友……也可以表示很多内容,凡是符合平均分、分成2份、拿1份这三个要点,都可以用表示。
(生汇报,如图7)
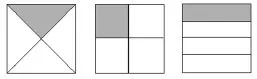
图7
师:观察大家表示的,有什么不同?又有什么相同?
生:形状各不相同,但都是平均分、分成4份、拿1份。
师:看来大家已经明白了的意思,那判断一下下面图形里的涂色部分能用表示吗?(如图8)

图8
师:大家还创造了哪些不同的新数?
……
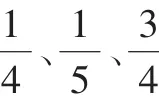
三、注重概念创生,经历过程深化认识
师:当用1表示都嫌大时,我们一起创造了这些新的数,这些新的数有一个共同的名字,你们知道吗?
生:几分之几数。
生:全分之几数。
生:分数。
师:多好的想法,能说说这样取名的道理吗?
生:今天认识的新的数,都是表示一个物体的几份中的几份,所以我把它叫作“几分之几数”。
生:我是这样想的,今天学习的数,都是把一个物体平均分成几份,拿全部份数中的几份,所以我给它取名为“全分之几数”。
生:我是观察“分”字,发现这个字的下面是一个“刀”字,联想到今天得到的数都是分出来的,所以叫“分数”。
师:分数——多好的名字,先分后数,与数学家的想法不谋而合。分数,它的各个部分都有自己的名字,谁来介绍一下分数各部分的名称?
(生答略)
师:孩子们,当用1表示都嫌大时,我们就可以用——分数来表示。分数在生活中不常见,它喜欢悄悄地藏在某个角落里,需要我们用数学的眼光去发现。接下来我们一起欣赏一段《蒙牛:一杯牛奶的责任》广告,看谁能从中找到分数?
师:你从广告中获得了什么数学信息?
生:扫15个二维码可以换一杯牛奶。
师:你能从中发现分数吗?
……
师:孩子们,这节课的学习就要结束了,回顾一下这节课的学习,你觉得有哪些收获?
(生答略)
师:概括得很好。孩子们,今天我们认识的分数,在历史上,与自然数一样古老,让我们一起了解一下分数的发展史。
(介绍分数演变的历史)
教学思考:今天的数学课堂肯定没有办法“原样重复”历史上的重大时刻,但是我们可以通过模拟情境创设,营造“危机时刻”,造成强烈的认知冲突,以此激发儿童“重新命名”新概念的欲望,让数学观念得以“诞生”。从儿童的角度讲,就是他们自己的发明和创造!
