定积分中的数学思想

定积分中的数学思想

■江苏省太仓市明德高级中学 王佩其

任何数学问题都离不开基本的思想方法,定积分也不例外。定积分的背景与应用中蕴含着数形结合思想,定积分的定义中蕴含着以直代曲的转化思想。而变化的定积分,往往和函数、方程联系在一起,蕴含着分类讨论思想。

1.数形结合思想

抛物线y=a x2+b x在第一象限

内与直线x+y=4相切,此抛物线与x轴所围成图形的面积记为S,求使S达到最大值时a、b的值,并求Smax。

解析：依题设可知抛物线为开口方向向下,它与x轴的交点的横坐标分别为x1=0,

又直线x+y=4与抛物线y=a x2+b x相切,即它们有唯一的公共点。

令S'(b)=0。当b＞0时得唯一驻点b =3,且当0＜b＜3时,S'(b)＞0;当b＞3时, S'(b)＜0,故在b=3时,S(b)取得极大值,也是最大值,此时a=-1,b=3,S取得最大

2.分类讨论思想

已知抛物线y=a x2(a＞0),将以(0,0),(b,0),(b,h),(0,h)为顶点的矩形分成两部分,其面积之比为1∶2,试求抛物线方程中的系数a的值。

解析：分两种情况讨论：

(1)如图1,S1

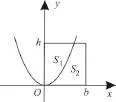
图1

(2)如图2知,S1由题意知,解得

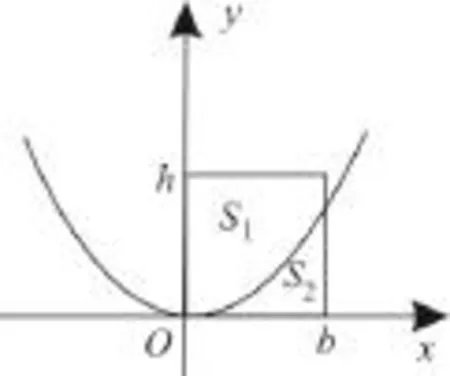
图2

3.函数与方程的思想

已知函数y=a x2+b x通过点(1,2),与y=-x2+2x有一个交点(x1,0),且a＜0,x1＞0。

(1)求y=a x2+b x与y=-x2+2x所围的面积S;

(2)a、b为何值时,S取得最小值?

解析：(1)题意知x=1时,y=2,故a+b =2,即b=2-a,从而y=a(x2-x)+2x。两个图像的交点横坐标为0知a＜0,x1＞0,由此可得1+a＜0,即a＜-1。两图像所围成的面积：在

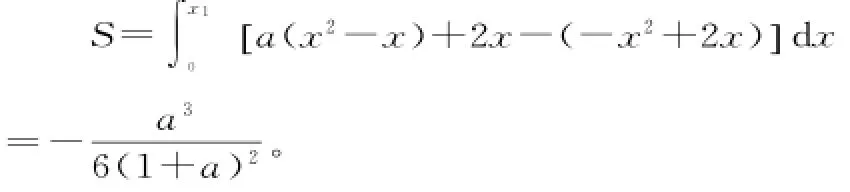
(责任编辑 徐利杰)