“求其源，诉其真”：更“接地气”的数学课堂

2017-05-05满斌

小学教学设计(数学) 2017年5期

满斌

《数学课程标准（2011年版）》关于教材编写建议中指出：数学教材为学生的数学学习活动提供了学习主题、基本线索和知识结构，是实现数学课程目标、实施数学教学的重要资源。对于教师而言，要合理地把握数学教材，剖析数学知识的“来龙去脉”，力求追本溯源，以实现数学课堂的优化。

一、寻求教材的根源，诉说其“纯真”

教师在处理教材时，既要尊重教材，也要创造性地使用教材。只有将教材知识的根源熟记于心，在教学中才会讲得“真切”，说得“真实”，教学才会“有本可依”。只有把握这些，教师才能诉之精华，讲之到位。数学教师要有对自己所教的学科有追本溯源的态度，在变中找不变的继承与支撑点，学会回到原点看问题。教材是“教学之本”，寻求教材的根源，寻找专家教材设计的意图，是教师备好课的基础，旨在体现课堂教学的“纯真”。

如：在四年级上册《三角形》单元后的练习题中，有这样一道题：

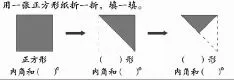
学生完成填空之后，教师并没有着急学习下一题，而是这样处理的：

师：做完这道题后你明白了什么？

生：我知道正方形内角和是360°。

生：发现三角形的大小在变化，但三角形的内角和不受影响，都是180°。

师：说得非常好。题目为什么要将正方形和三角形放在一起呢？似乎还要告诉我们什么呢？（学生陷入思考中）

生：我知道了，正方形变成三角形，它的内角和就变了。

生：哦，是的呀！

师：图形的种类变了，内角和就变了。内角和与图形的大小没有关系。

生：不对，正方形的内角和是360°，而长方形的内角和也是360°。

师：这是什么原因呢？难道我们刚才说的结论错了？

生：正方形是特殊的长方形，图形的种类没变。

生：正方形和长方形都是四边形，四边形的内角和是360°。

师：是吗？你们能再举个例子吗？

生：平行四边形。

（教师在黑板上画出一个平行四边形）

师：它的内角和是360°吗？

生：不知道，得量一下。

……

从此环节设计中看出，教师将教材练习进行了“进一步加工处理”，并不是直接就题讲题，一带而过，而是充分理解教材，抓住教材根源，让学生深入思考，有效地利用教材，利用好本题。不难看出，教师在理解和处理教材时，把握其根源，发挥教材的价值，呈现出题目的价值，将本题教学价值最大化。教学过程中，教师没有附加的“修饰”和“渲染”，而是利用教材一题，师生的问答，步步深入思考和探索，促进学生思维的发展，诉其教学的“纯真”。由此可见，课堂教学期望的是学生“自由、自主、自信”地开展学习活动，就需要教师在备课中准确把握知识的本质属性，合理设置学习目标。在此基础之上，“把目标变成学习任务，把教材根源变成学生知识的生长点”，让学生在课堂的学习活动中“善做、真学”。

二、追求知识的起源，诉说其“归真”

数学知识的教学应追求其起源，因为数学知识有着前后联系、一个整体之说，内在的知识体系前后关联，每一个新知的学习，都离不开旧知的铺垫。因而教师在教学设计中要有挖掘知识起源的精神。

例如：六年级《圆的认识》中的一个教学片断：

师：其实，早在两千多年前，我国古代就有了关于圆的精确记载，墨子在他的著作中这样描述道：“圆，一中同长也。”你能理解其中的意思吗？

生：一中是指一个圆心，同长则指半径或直径同样长。

师：而中国古代的这一发现，要比西方整整早一千多年。听到这里，同学们感觉如何？

生：特别自豪和骄傲。

生：我觉得我国古代的人民非常有智慧。

师：其实，我国古代关于圆的研究和记载还远不止这些。《周髀算经》中有这样一个记载“圆出于方，方出于矩”，是说最初的圆是由正方形不断地切割而来。现在如果告诉你正方形的边长是6厘米，你能获得关于圆的哪些信息？

师：说起中国古代的圆，下面的这幅图案十分特别（图略），认识吗？

生：阴阳太极图。

师：细细看来，阴阳太极原来是由一个大圆和两个同样大的小圆组合而成。现在如果告诉你小圆的半径是3厘米，你又能知道些什么呢？

……

在这“圆的历史文化”一环节中，充分看出教师追求知识的起源及内在的关系，将知识结构进一步提炼和完善，表达了对数学文化的一种解读，努力将圆所具有的文化特性浸润于学生的心间，成了学生数学成长的不竭动力源泉。

数学知识体系基本上是由概念、判断和推理构成的。概念教学首要是保证概念理解上的确定性和真实性，要追求知识的起源，揭示其内涵和外延，了解其概念之间的关系。课堂教学中切不可模棱两可、似是而非，更不可自相矛盾。由此，抓住了知识的“生长点”，体现数学知识起源中的文化特性，此教学过程的真实发生必将利于数学课堂教学“归于其真”。