三体船分段模型波浪载荷试验研究

任慧龙，田 博，仲 琦

（哈尔滨工程大学 船舶工程学院，哈尔滨 150001）

三体船分段模型波浪载荷试验研究

任慧龙，田 博，仲 琦

（哈尔滨工程大学 船舶工程学院，哈尔滨 150001）

三体船的主体与连接桥结构的波浪载荷特性是船舶结构设计者非常关注的问题，目前对于这些载荷特性进行较为全面的模型试验研究在国内很少。该文在拖曳水池和方形水池开展了某三体船的分段模型试验，详细介绍了分段模型的设计原则，对于纵向载荷和横向载荷的测量采用不同的分段布置形式。通过对试验数据的分析及与理论计算的对比，对三体船横摇运动非线性修正方法加以改进，同时研究了该三体船的船舯横剖面和连接桥纵剖面的波浪载荷特征，得出了一些结论，为船舶结构设计提供了确定设计载荷的依据。

三体船；分段模型试验；波浪载荷

0 引 言

近年来，高性能船舶得到了深入的研究和广泛应用，高速三体船就是较受关注的船型之一。布置在主船体两侧的片体，使得三体船的兴波阻力要比常规船型小很多，横向的稳定性得以增加。 同时，三体船型的耐波性能良好，不仅具有相对平缓的横摇周期，不会发生双体船易晕船的现象，且船体的纵摇和升沉较小。优良的水动力性能使得该船型在民用方面颇受青睐，作为军用船型，还具有良好的防护能力、破损稳性以及隐蔽性，宽阔的甲板可为各类作战模块提供更多的布置方案，其军事应用前景广阔。

由于连接桥的存在以及片体的干扰，三体船的载荷分布及幅值与常规单体排水式船舶相比均有所不同[1-2]。而目前国内关于三体船波浪载荷试验的相关研究并不多，因此，本文将针对一高速三体船的分段波浪载荷试验进行研究，通过对试验数据的分析，总结该三体船的波浪载荷特征，为结构设计提供确定其设计载荷的依据。

1 三体船试验模型设计

本文三体船模型设计的主要相似关系如下：

A.模型与实船外形（包括水线以上及甲板上层建筑等）几何相似；

B.模型与实船沿船长的纵向重量分布及转动惯量或转动半径相似；

C.模型承受总纵弯曲的构件，其沿船长的剖面惯性矩与材料弹性模数的乘积按缩尺的五次方缩小，以保证弯曲振动的频率及振动形式的相似；

D.试验时按实船傅汝德数及船模缩尺的波浪要素来进行。

基于以上原则，试验模型的主尺度见表1所示。

表1 模型主尺度Ta.1 M ain parameters of themodel

与单体船相比，三体船由于其特殊的结构形式，导致其除了承受垂向弯矩、水平弯矩、纵向扭矩等纵向分布的载荷外，连接桥结构还要承受分离弯矩、横向扭矩等横向分布的载荷。因此，分段划分应与测量载荷剖面相适应，其测量剖面不仅包含横向剖面还应包含纵向剖面。

如图1所示，主船模纵向分为7个分段（分割位置分别为3站、5站、6.75站、9.25站、11站和15站），片体分为2段（划分位置为15站）；模型横向分为3段，即沿横向分别为左侧片体、主体以及右侧片体。湿甲板作为片体的延伸而没有彼此再分段，主要考虑以下两点：第一、连接桥湿甲板在高海况下会出现入水或砰击等情况，故湿甲板必须在模型中有所体现；第二、由直接计算和规范可知，承受分离弯矩较大的位置在主体和连接桥相交处[3]。因此，本文设计中将湿甲板与片体的载荷共同进行测量。

在设计主体的测量梁时，通过调整梁截面的尺寸，保证模型与实船结构动力相似。采用MSC.Nastran对测量梁进行模态分析，可得到其各阶模态的固有频率，基于模态计算的结果设计主体测量梁[4-5]。

需要注意的是，除了上层建筑之外，三体船的连接桥与片体都部分参与总纵强度，因此，在设计主体测量梁时，需要分别从刚度和首阶固有频率相似两方面来考虑。先根据主体（不含上层建筑）的刚度设计测量梁尺寸，再根据首阶垂向固有频率，将上层建筑、连接桥及片体等刚度补偿到测量梁的刚度上。本文保证模型与实船首阶垂向固有频率相似，最终测量梁频率的误差如表2所示。

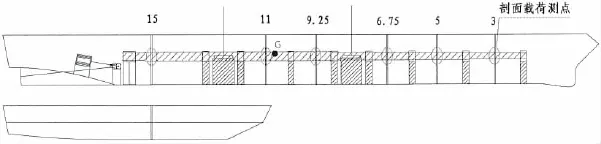
图1 分段模型示意图Fig.1 Sketch picture of the segmentsmodel

表2 垂向固有频率比较（干模态）Tab.2 Comparison between theoretical and experimental vertical natural frequency of themodel(drymode)

在设计片体测量梁时，由于分段数较少，本文暂不考虑其弹性效应，在大致满足船体该剖面的刚度的前提下，保证足够的强度，并保证足够的测量精度，即梁表面的应力不会过小。

在测量纵向分布载荷时，为较好地保证力传递的效果，将片体分为两段分别与主体连接。但在测量横向分布载荷时，需要将片体连成一个整体来测量，并考虑到测量纵向、横向载荷时，分段方法以及测量方法难以统一。本文通过改变模型布置方式形成两种测量方案：测量沿纵向分布的载荷（垂向弯矩、水平弯矩和纵向扭矩）时，将片体两分段分别与对应的主船体部位相连，将片体视为主体的延伸，用以传递总体载荷；测量沿横向分布的载荷（连接桥横向扭矩、分离弯矩）时，将片体的前后两段用一根测量梁（可测量片体剖面载荷）连接，再用一个三分力传感器连接主体与片体，并测量整个片体产生的横向载荷。

2 模型波浪载荷的理论值计算

本文根据三体船的型值信息，以艉垂线和基线的交点为计算原点，通过Msc.Patran建立有限元网格，再通过接口程序将其转化为波浪载荷预报程序的水动力网格，见图2。

基于三维线性频率理论，根据实船质量分布建立分段质量模型，计算剖面的选取根据劳氏三体船中规范计算点的位置[3]，横剖面应计算垂向弯矩、水平弯矩、纵向扭矩等剖面载荷，纵剖面应计算分离弯矩、横向扭矩等剖面载荷。

为了与试验进行对比分析，本文计算点选取位置以试验为准。浪向角选取了从0°到180°，间隔45°一个浪向，共5个浪向，分别是迎浪（0°）、艏斜浪（45°）、正横浪（90°）、艉斜浪（135°）和随浪（180°）。

图2 模型水动力网格Fig.2 Hydrodynamicmesh of themodel

3 试验结果比较及分析

3.1 横摇运动非线性修正方法研究

在预报斜浪和横浪下产生的载荷成分时，横摇对预报结果影响较大[6]。因此，准确地预报横摇运动是计算三体船在横浪、斜浪中波浪载荷的重要问题。

目前在常见的横摇运动的非线性修正方法中，采用最为普遍的是临界阻尼修正系数法[5]。对于常规单体船来说，通过大量计算经验的积累，通常将临界阻尼修正系数取为0.05。而在计算三体船时，该系数的取法并不合理，三体船的临界阻尼修正系数一般会偏大，但由于计算实例极少，大部分文献中对此并未进行说明，个别文献中仍采用0.05进行计算。

本文采用不同修正系数对无航速下三体船横摇进行预报，并与试验进行对比，通过比较分析得到合理的临界阻尼修正系数，为后续载荷预报提供基础。图3、图4和表3为横浪与艏斜浪时采用不同修正系数的横摇预报值和试验值的对比。

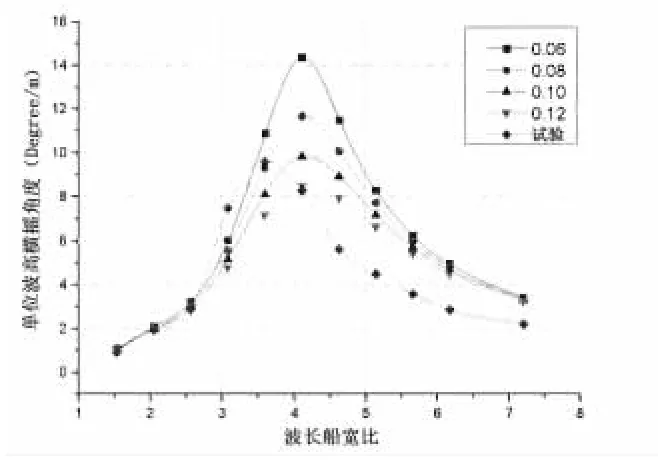
图3 横浪情况下横摇运动对比Fig.3 Comparison of rollmotion in beam sea

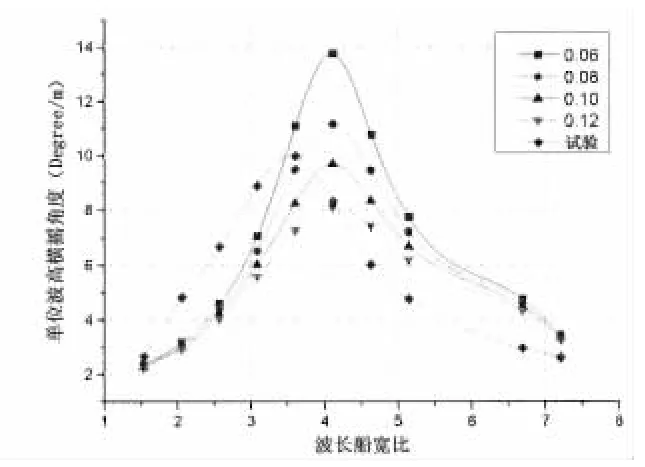
图4 艏斜浪情况下横摇运动对比Fig.4 Comparison of rollmotion in bow sea

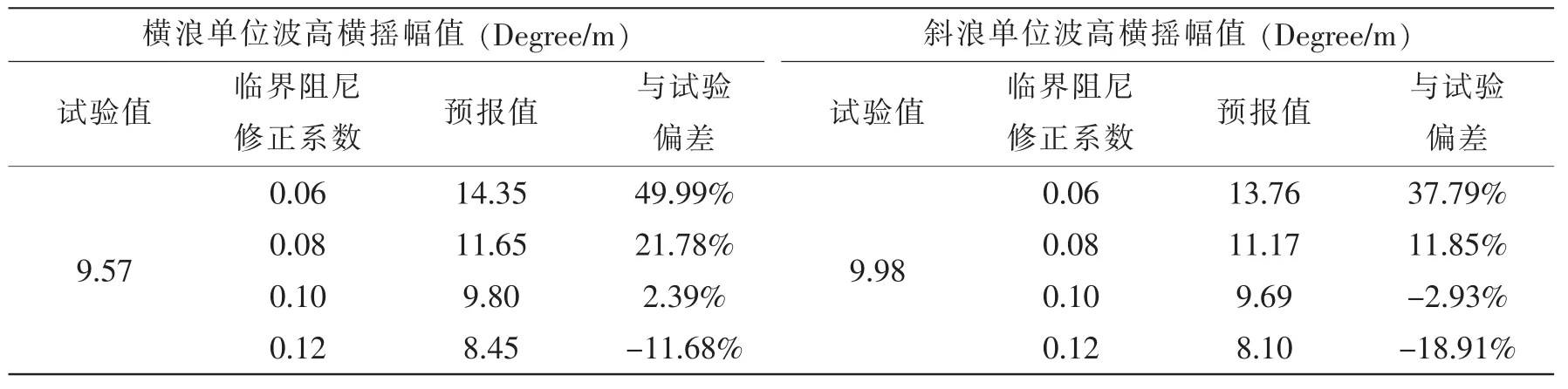
表3 横摇预报幅值与试验对比Tab.3 Com parison between theoretical and experim ental vertical natural

从结果比较中可以看出，当临界阻尼修正系数取为0.10时，预报的横摇幅值与试验值相差很小，仅不到3%。因此，后续对本型三体船的载荷计算时，临界阻尼修正系数将取为0.10。

3.2 纵向载荷理论预报与试验结果对比分析

本文选取船舯剖面（第11站）的垂向弯矩、水平弯矩及纵向扭矩等纵向分布载荷进行分析，按以下公式进行无因次化[3]：

式中：M为测量弯矩的幅值，M¯为无因次化弯矩幅值；Mn为测量扭矩的幅值，M¯n为无因次化扭矩幅值；ρ为水的密度，g为重力加速度，L为三体船主体设计水线长，B为三体船总宽，ζa为规则波波幅。

由于三维频率理论基于零航速格林函数，因此，本文主要研究零航速情况下理论值和实验值的比照。图5至图8为船舯剖面（第11站）在零航速不同浪向下的垂向弯矩，图9至图11为船舯剖面在零航速不同浪向下的水平弯矩，图12至图14为船舯剖面在零航速不同浪向下的纵向扭矩。

从图中可以看出，垂向弯矩RAO的理论值与预报值随波长变化的趋势大体一致，其中艏斜浪和艉斜浪的数据吻合较好，对于迎浪和随浪，当波长大于0.8倍的船长后，理论值比试验值偏大，最大相差约20%，造成此误差的原因之一为试验场地的不同，本文中迎浪和随浪试验在拖曳水池中进行，由于三体船的宽度较大，可能会受到池壁的影响。水平弯矩RAO的理论值与试验值随波长变化的趋势大体相似，对于艉斜浪，当波长大于0.5倍的船长后，试验值比理论值增加较多。纵向扭矩RAO的理论值与试验值随波长的趋势大体相似，但存在一定的差异，原因之一在于扭矩的测量比弯矩的测量更为复杂，由于应变片布置等原因产生误差。各种纵向载荷试验值在艏斜浪和艉斜浪下峰值的位置和量值大体相同。

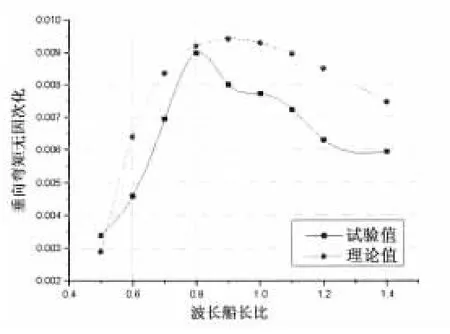
图5 垂向弯矩结果比较（迎浪）Fig.5 Comparison of vertical bendingmoment in heading sea

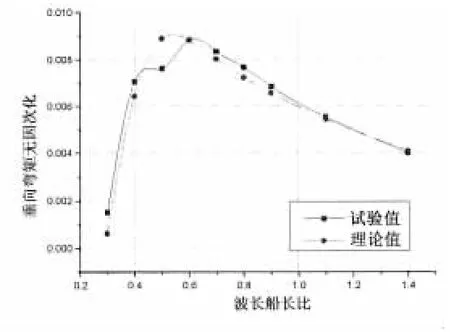
图6 垂向弯矩结果比较（艏斜浪）Fig.6 Comparison of vertical bendingmoment in bow sea

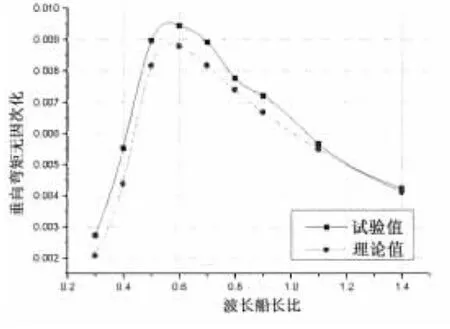
图7 垂向弯矩结果比较（艉斜浪） Fig.7 Comparison of vertical bendingmoment in quartering sea

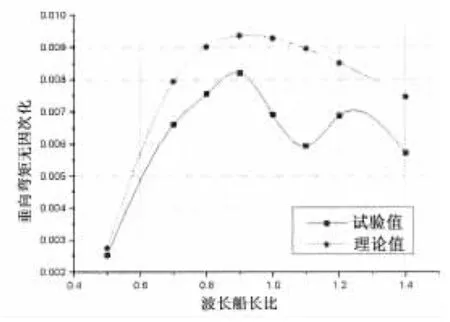
图8 垂向弯矩结果比较（随浪）Fig.8 Comparison of vertical bendingmoment in following sea

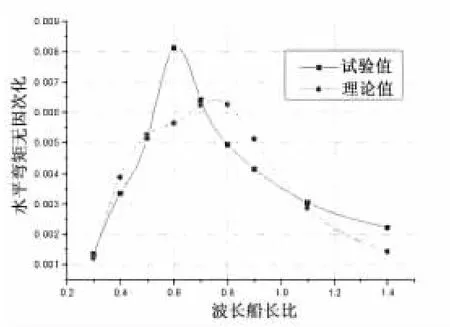
图9 水平弯矩结果比较（艏斜浪）Fig.9 Comparison of horizontal bendingmoment in bow sea

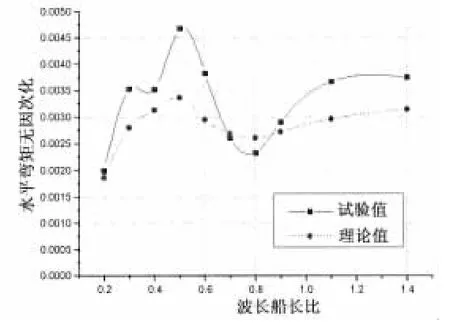
图10 水平弯矩结果比较（横浪）Fig.10 Comparison of horizontal bendingmoment in beam sea

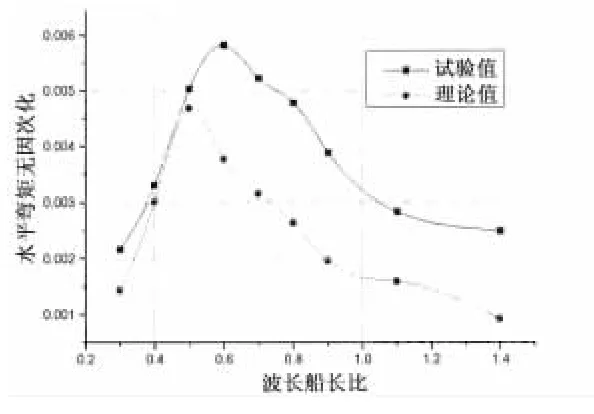
图11 纵向扭矩结果比较（艉斜浪）Fig.11 Comparison of horizontal bendingmoment in quartering sea

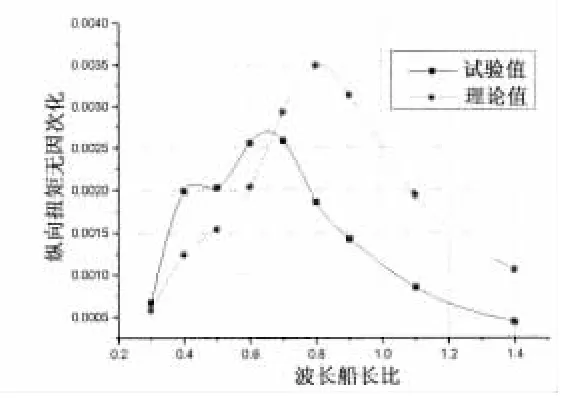
图12 纵向扭矩结果比较（艏斜浪）Fig.12 Comparison of longitudinal torsionmoment in bow sea

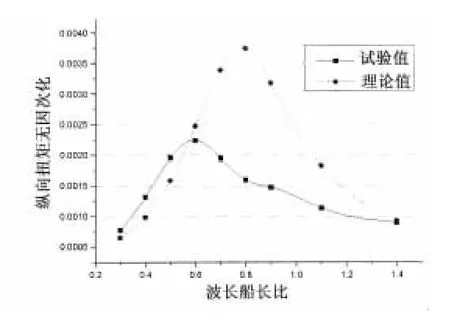
图14 纵向扭矩结果比较（艉斜浪）Fig.14 Comparison of longitudinal torsionmoment in quartering sea

3.3 横向载荷理论预报与试验结果对比分析

本文选取主体与连接桥连接的纵剖面的分离弯矩和横向扭矩等横向分布载荷进行分析，无因次化方法与之前所述相同。图15至图17为纵剖面在零航速不同浪向下的分离弯矩结果对比，图18至图20为纵剖面在零航速不同浪向下的横向扭矩的结果对比。

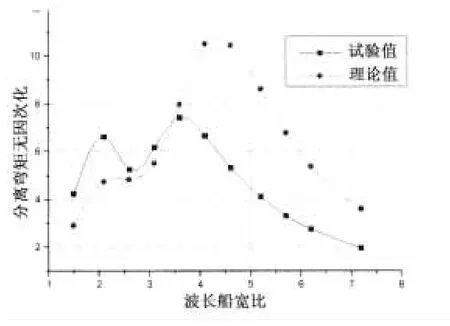
图15 分离弯矩结果比较（艏斜浪）Fig.15 Comparison of separate bendingmoment in bow sea

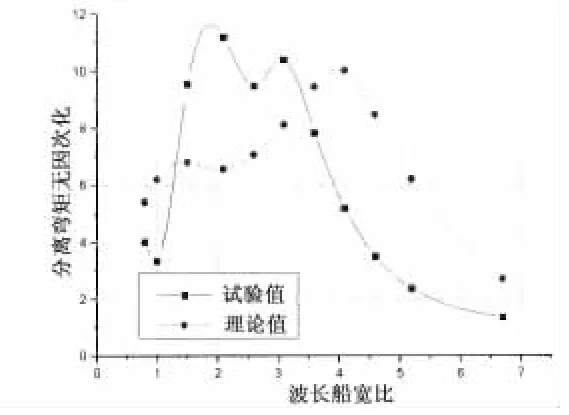
图16 分离弯矩结果比较（横浪）Fig.16 Comparison of separate bendingmoment in beam sea

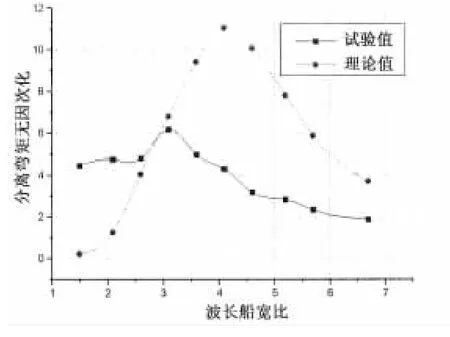
图17 分离弯矩结果比较（艉斜浪）Fig.17 Comparison of separate bendingmoment in quartering sea

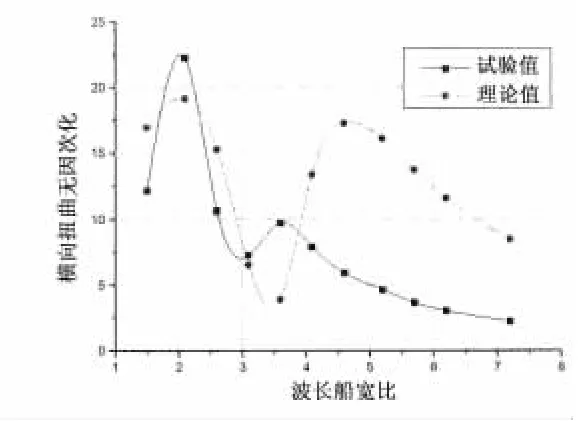
图18 横向扭矩结果比较（艏斜浪）Fig.18 Comparison of transverse torsionmoment in bow sea

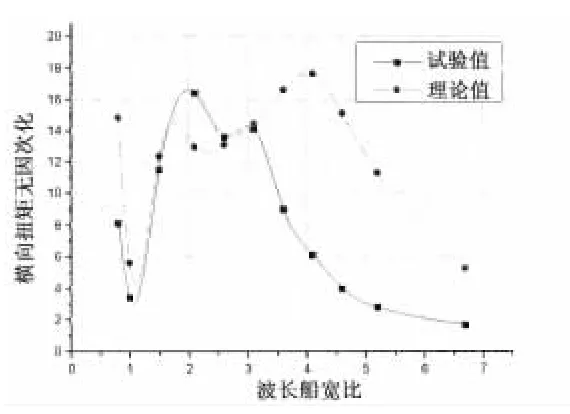
图19 横向扭矩结果比较（横浪）Fig.19 Comparison of transverse torsionmoment in beam sea

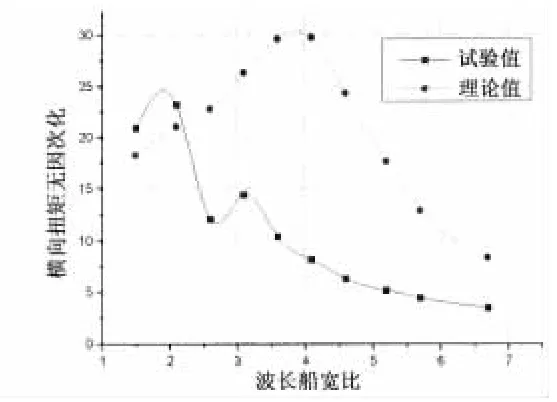
图20 横向扭矩结果比较（艉斜浪）Fig.20 Comparison of transverse torsionmoment in quartering sea

从图中可以看出，相对于横剖面的纵向载荷而言，纵剖面的横向载荷理论值与试验值的RAO曲线无论在趋势还是在峰值上都存在一定差异，尤其在艉斜浪下，理论值与试验值差距较大。对于二者之间的差异主要有两个原因：一是频域理论无法考虑三体船片体的影响和主体之间的相互影响，利用现有的单体船型的计算方法计算三体船纵剖面的横向载荷必然存在误差；二是实验过程中，横向载荷的测量比纵向载荷更为复杂，由于仪器的安装和精度等原因导致测量结果存在误差。也可以看出，在艏斜浪和艉斜浪下，横向载荷试验值的峰值的位置和量值大体相同。

4 结 论

本文将试验技术与理论计算相结合，详细介绍了三体船分段模型的设计原则和载荷测量方法，并对某三体船的试验结果进行了处理，通过比较分析，可以得到如下结论：

（1）通过不同修正系数对无航速下三体船横摇进行预报，并与试验进行对比可知，临界阻尼修正系数选取0.05预报三体船横摇运动结果偏大，本文建议选取0.10。

（2）对于纵向分布载荷，垂向弯矩的预报结果吻合较好，而水平弯矩和纵向扭矩稍差，与其他浪向相比，横浪的预报结果吻合程度稍差。

（3）对于横向分布载荷，理论预报都与试验结果存在一定差异。

（4）总体而言，纵向载荷的预报结果优于横向载荷，弯矩的预报结果优于扭矩。

通过本文的研究可知，现有单体船的载荷预报理论对于三体船载荷预报结果与试验值相比存在一定的误差，对于三体船片体和主体之间的影响还有待于更深入的理论研究。同时，本文对三体船的波浪载荷模型试验技术的研究，对于后续总结三体船波浪载荷特征，确定三体船设计载荷等工作奠定了基础。

[1]耿彦超,汪雪良.三体船波浪载荷模型试验研究[C]//中国钢结构协会海洋钢结构分会2010年学术会议暨第六届理事会第三次会议论文集.中国河南洛阳,2010.

[2]汪雪良,胡嘉骏.三体船波浪载荷模型测试技术研究[C]//七届更迭三十回眸—第七届船舶力学学术委员会全体会议论文集.中国四川成都,2010.

[3]Rules for the Classification of Trimarans[S].London:LR,2006.

[4]MSC/Nastran Reference Manual.MSC.Software Corporation[M].Germany:MSC.Software GmbH,2003:45-61.

[5]Zhang JW.Roll damping characteristics of a trimaran displacement ship[J].Int Shipbuild.Progr.46,1999,448:445-472.

[6]Journee JM J.Theoreticalmanual of SEAWAY[S].Delft University of Technology Shipydromechanic Laboratory,2001: 148-153.

W ave loads experimental investigation of segmented model of a trimaran

REN Hui-long,TIAN Bo,ZHONG Qi
(College of Shipbuilding Engineering,Harbin Engineering University,Harbin 150001,China)

The wave loads characteristic of trimaran’smain hull and cross structure is a great concern to ship structure designers,but comprehensivemodel tests are researched little in China currently.In thiswork, a trimaran’s segmented model testwas carried out in a towing tank and a square tank,the design principle of segmented model was introduced in detail,and different segmented models were designed formeasuring longitudinal loads and transverse loads.According to analysis of the experimental values and comparison with the results of theoretical calculation,the nonlinearmethod of rollmotion prediction was improved,and the wave loads characteristics of midship transverse section and cross structure longisection were reserached.Finally,some conclusions were obtained,which can be the basis for the design loads of this trimaran to ship structure designers.

trimaran;segmented model experiment;wave loads

U661.3

：Adoi:10.3969/j.issn.1007-7294.2017.01.001

2016-06-24

国家高技术船舶科研项目；国家自然科学基金项目（50809019）；国防基础科研项目（A2420061100）

任慧龙（1965-），男，教授，博士生导师，E-mail：renhuilong@263.net；

田 博（1990-），男，博士研究生。

1007-7294（2017）01-0001-07