两自由度可调非线性减振器1)
2017-05-03杨柳杨绍普杨月婷
杨柳杨绍普杨月婷
∗(北京交通大学机械工程学院,北京100044)
†(石家庄铁道大学机械工程学院,石家庄050043)
两自由度可调非线性减振器1)
杨柳∗,2)杨柳,博士生,主要研究方向为非线性振动.E-mail:yang 8873@126.com杨绍普†杨月婷†
∗(北京交通大学机械工程学院,北京100044)
†(石家庄铁道大学机械工程学院,石家庄050043)
研究了可调非线性减振器的优化设计.基于哈密尔顿最小势能原理建立非线性动力学模型,系统局域参数内,实现非线性系统幅值优化.利用平均法求解可调非线性减振器频响方程.分析系统解的稳定性,优化系统参数,降低系统幅值响应.
可调,非线性,稳定性,优化
振动是一种常见现象,经常引起结构的疲劳破坏,影响正常使用.为了减小机器振动,吸振器已经有了广泛的应用及发展.
本文建立了完整的动态模型.通过对系统稳定性分析及系统可调参数下的优化,设计非线性可调吸振器.
Ormondroyd等[1]首次提出线性吸振器的参数设计及其优化方法.Warbuton对线性吸振器进行优化方法的设计及优化参数的改进[2],如何更加有效地设计吸振器以及保证减振的效果成为研究重点.首先,线性吸振器的发展,对系统提出不同的优化方案[3],系统参数设计已经有了精确解[4].然而,由于频率间距较窄,一旦激振频率偏离调谐点就产生较大振动.为了解决这个问题,一些研究者开始研究非线性吸振器[5].之后,非线性吸振器得到发展,最初,Arnold[6]考虑无阻尼立方非线性弹簧吸振器,在相应的非线性条件下不同参数优化方法有了发展. Natsiavas[7]研究了非线性稳定性分析,及在软、硬刚度下,非线性吸振器的动态响应.近年来,在系统内共振条件下,出现饱和吸振现象,降低了系统的响应[810].另外,非线性也使得系统在一定条件下出现不稳定、分岔及多解情况,降低了系统幅值.
1 动力学模型
图1为可调非线性系统.x1为主质量m1的位移,x2为振子m2的位移
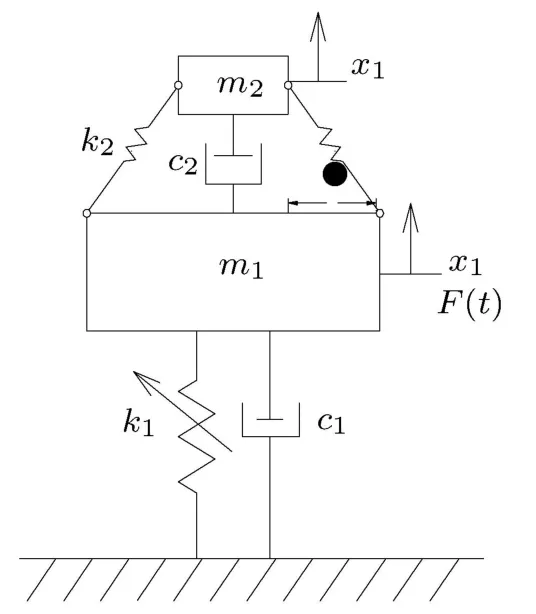
图1 可调非线性减振模型
基于可调非线性减振器的动能及势能,利用哈密尔顿最小势能原理,减振动态模型为
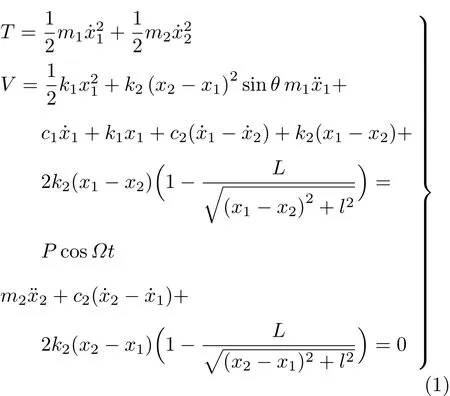
其中,l为弹簧在横向的投影长度,为可调因数;L为弹簧k2的实际伸长量.
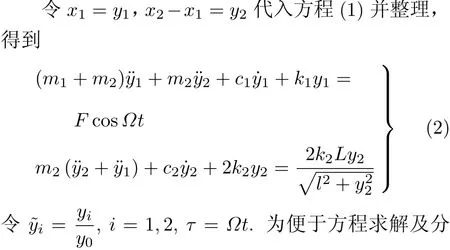
下面对方程进行简化和无量纲化析非线性项,对方程做二阶近似处理展开,系统矩阵形式为
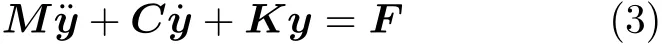
其中,质量、阻尼、刚度矩阵及相关系数为
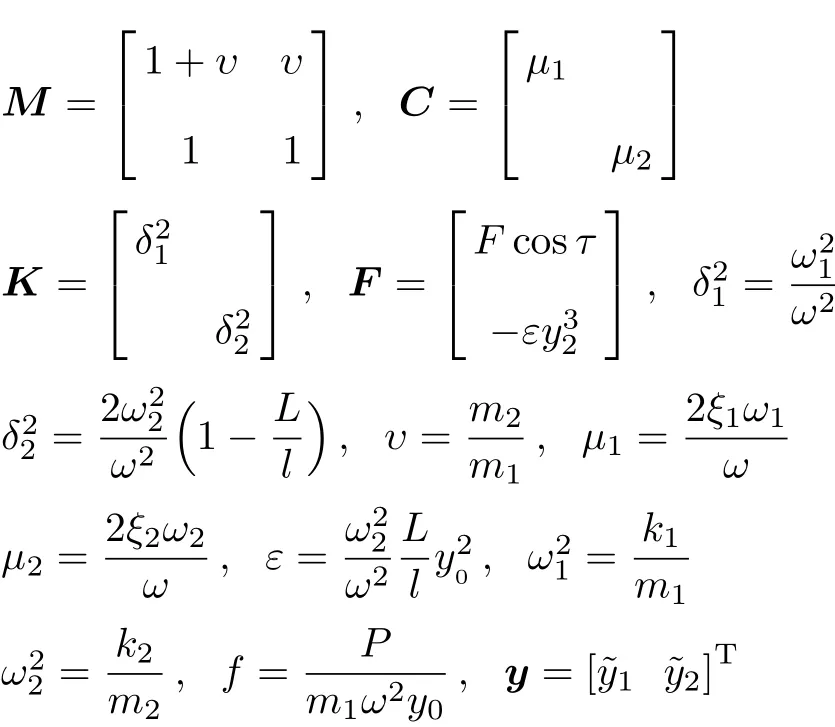
2 近似求解
利用平均法,对系统方程稳定解做近似展开,解的形式
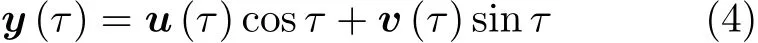
其中,u(τ),v(τ)为慢时变函数
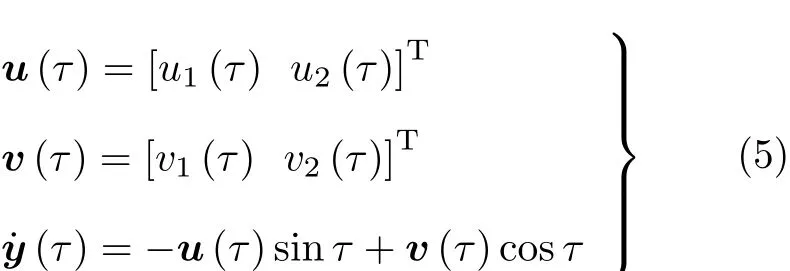
则
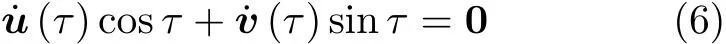
由式(5)得
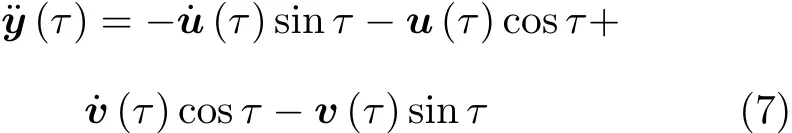
将式(7),式(5),式(4)代入式(3)整理得
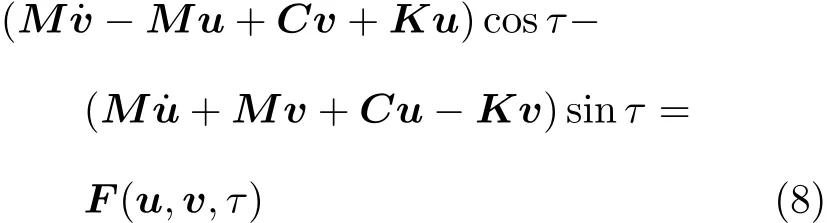
方程(6)乘以M cosτ,式(8)乘以-sinτ,将两式相加,在周期内积分取平均,化简得
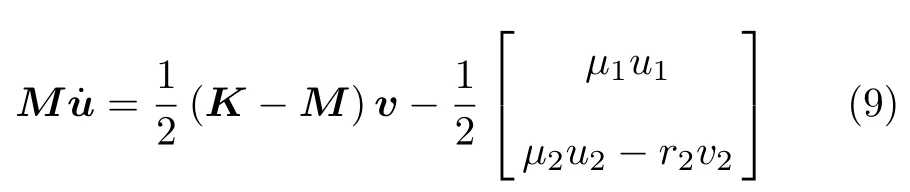
方程(6)乘以M sinτ,式(8)乘以cosτ,将两式相加,在周期内积分取平均,化简得
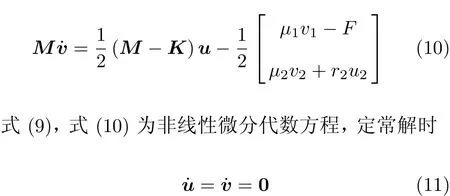
整理式(11)得到
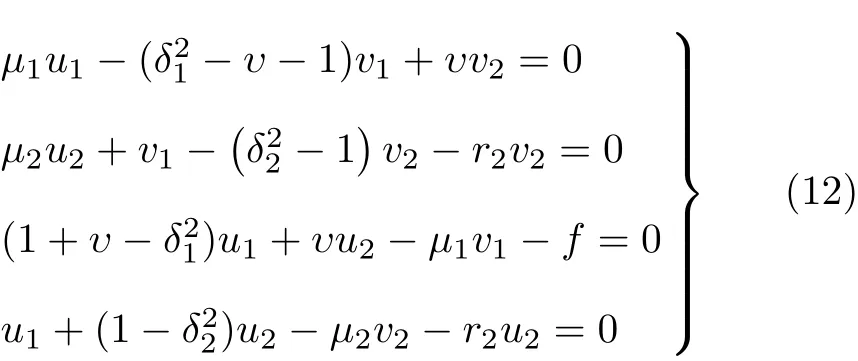
3 稳定域分析
在小扰动下,方程(12)为

其中

根据Roth判据
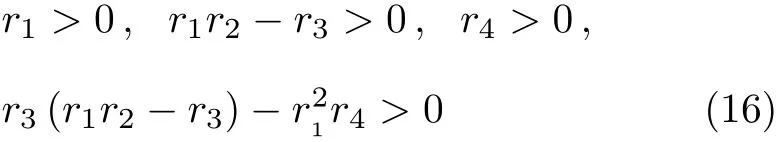
4 参数下系统方程的响应及其优化
4.1 系统幅频响应解析解
令主质量幅值R2及振子R1幅值为
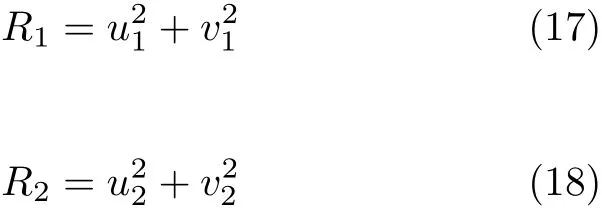
其中R2是高阶次方程隐函数公式
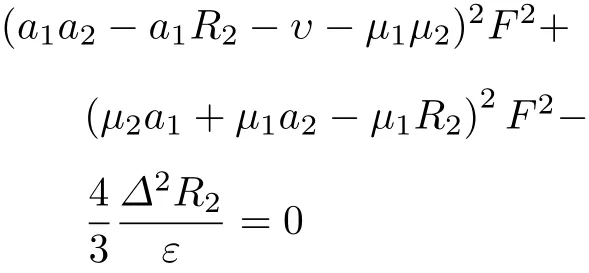
式中
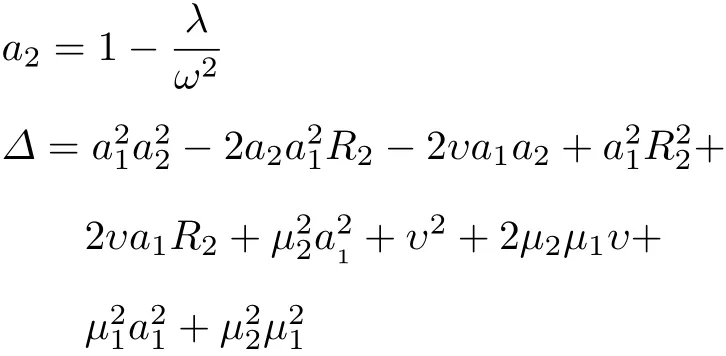
选取数据ξ1=0.02,ξ2=0.03,ε=0.01,f=0.1/ω2.如图2和图3所示,R1主质量系统的共振幅值响应较大,R2振子的幅频响应,振动幅值一定区域内存在多值解的情况,出现明显的不稳定性及幅值差较大,且共振峰值较大,可调节振子与主质量的减振效果不明显.
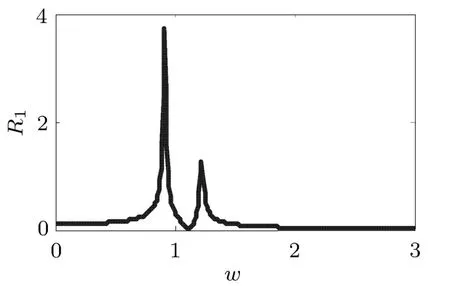
图2 主质量幅频响应
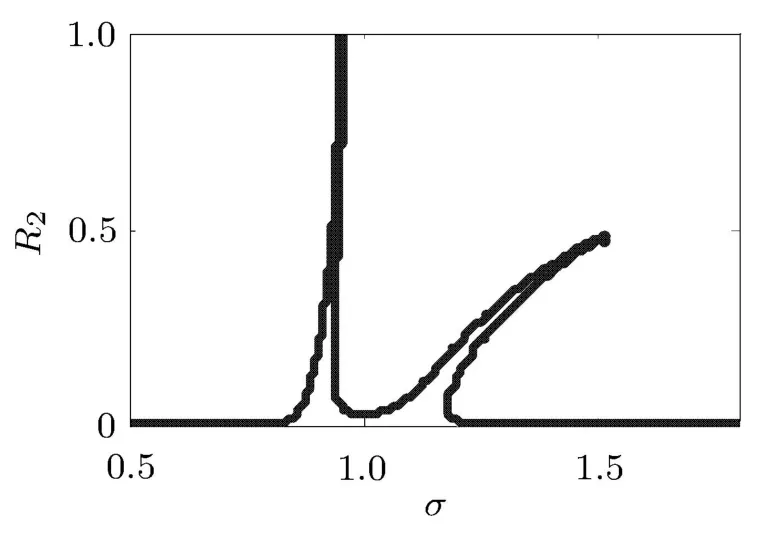
图3 振子幅频响应
4.2 系统优化参数
为了能更好的满足设计要求及稳定性,对系统目标函数进行H∞优化,如下
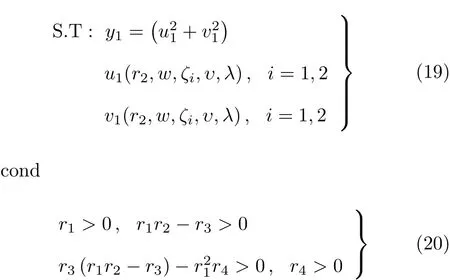
给定不同数值区间下ξ1,ξ2,λ,ε,f,系统参数在可行域(20)内,求解方程式(19)条件下的最优值问题.其中,参数变因子R2内的可行域[0,1],阻尼系数ξ1,ξ2设计区间:[0.01,0.2],频率比λ设计区间[0.5,3],质量比值参数υ区间为[0.04,0.2].
通过全局数值搜索,系统数值最优参数为:ξ1= 0.03,ξ2=0.03,λ=0.85,υ=0.05,ε=0.01.图4为主质量幅频响应.可知主质量系统经优化幅值得到明显的降低,系统峰值近似相等.
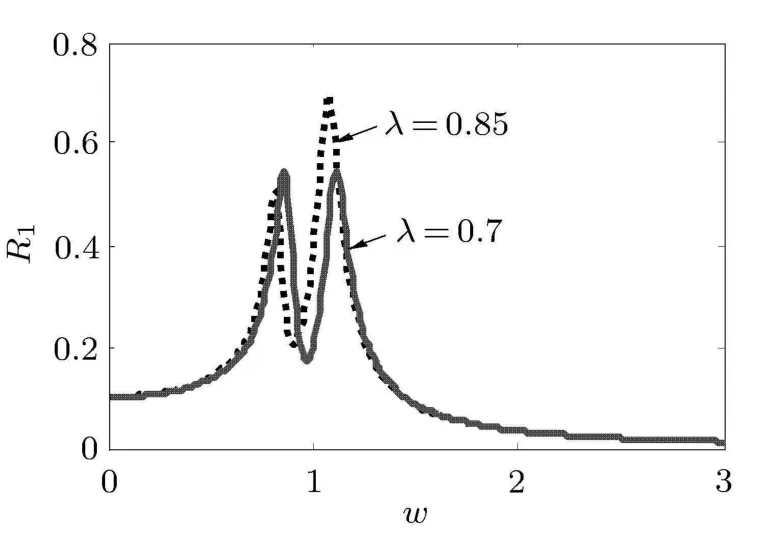
图4 主质量幅频响应
在图5中,虚线为线性优化条件下近似解析解,实线为非线性优化条件下数值结果.不同优化条件下平均幅值差比为10%,可调非线项对系统的优化效果明显.
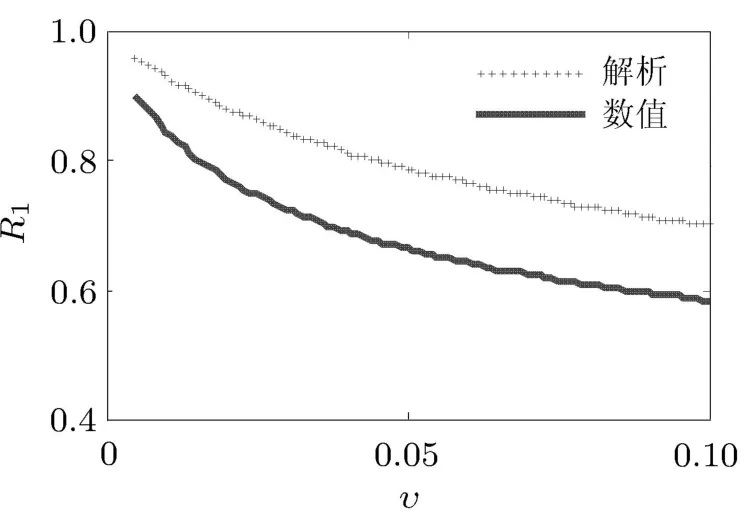
图5 主质量幅值
图6~图9为可调振子幅值响应.给定系统优化参数:ξ1=0.03,ξ2=0.03,λ=0.85,υ=0.05,ε=0.01,振子共振幅值出现近似相等.
图6为频率比λ对振子的影响,随着频率比的增加,振子幅值减小,共振区间向右平移.在满足系统优化条件下,频率比对振子幅值的影响并不明显.
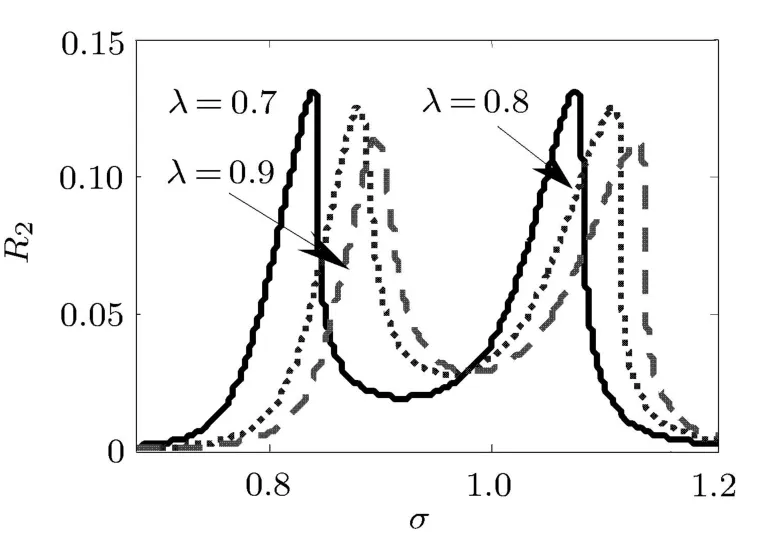
图6 频率比λ参数的影响
图7为阻尼系数ξ2对振子的影响.随着阻尼系数的增加,振子幅值明显减小.
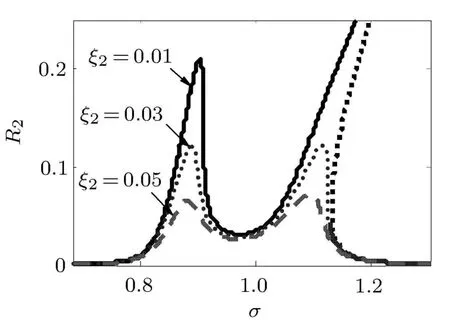
图7 阻尼系数ξ2参数的影响
图8为质量比υ对振子的影响,随υ的增加,振子幅值减小,共振区间增大.
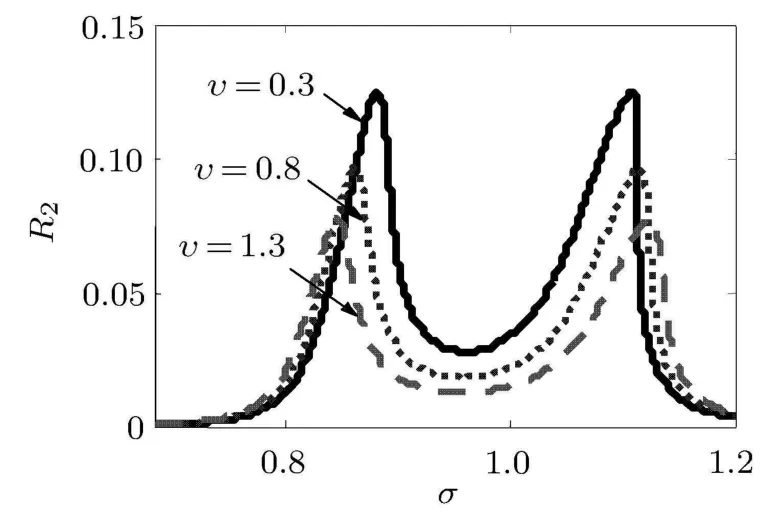
图8 质量比υ参数的影响
图9中,ε(k2,L,l)是可调节因子,随着ε的增加,振子的响应变大.在软刚度下,振子幅值降低明显.通过改变参数l值的大小,可调节减振效果.
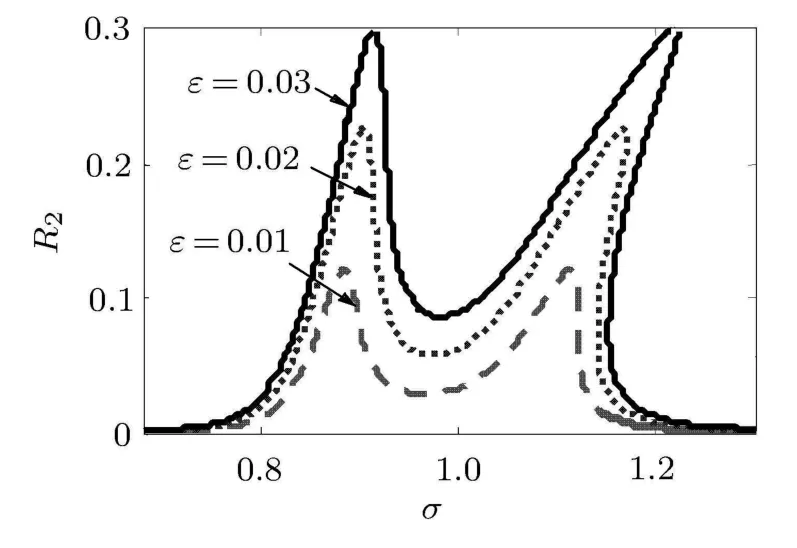
图9 可调参数ε的影响
5 总结
研究了可调非线性振子被动减振器.建立可调节的非线性减振模型,分析非线性条件下幅频响应函数主要影响参数,在满足稳定性条件下,优化系统参数,可使主质量系统及振子幅值得到明显降低.在被动减振下,该模型为工程实际应用及其参数选取提供设计依据.
1 Ormondroyd J,Den Hartog JP.The theory of the dynamic vibration absorber.Transactions of the American Society of Mechanical Engineers,1928,50:9-22
2 Lee KY,Renshaw A.Stability analysis or parametrically excited systems using spectral collocation.Sound Vibration,2002,25:273-296
3 Asami T.Closed-form exact solution to h ptimization of dynamic vibration absorbers.ASME Journal of Vibration and Acoustics,2003,6:400-411
4 Roberson RE.Synthesis of a non-linear dynamic vibration absorber.Journal of the Franklin Institute,1952,254:205-220
5 Pipes LA.Analysis of a non-linear dynamic vibration absorber.Journal of Applied Mechanics,1953,20:515-518
6 Arnold FR.Steady state behavior of systems provided with non-linear dynamic vibration absorbers.Journal of Applied Mechanics,1955,22:487-492
7 Natsiavas S.Steady state oscillations and stability of nonlinear dynamic vibration absorbers.Journal Sound and Vibration,2005,286:697-727
8 Shen YJ,Wang L,Yang SP.Nonlinear dynamical analysis and parameters optimization of four semi-active on-o ff dynamic vibration absorbers.Journal of Vibration and Control,2012,19:143-160
9 Rahnavard M,Hashemi M,Farahmand F,et al.Designing a hand rest tremor dynamic vibration absorber using H2 optimization method.Mech Sci Technol,2015,28:1609-1614
10 Shen YJ,Che L.Improved design of dynamic vibration absorber by using the inerter and its application in vehicle suspension.Journal of Sound and Vibration,2016,361: 143-160
(责任编辑:刘希国)
2-D TUNABLE NONLINEAR ABSORBER1)
YANG Liu∗,2)YANG Shaopu†YANG Yueting†∗(School of Mechanical Engineering,Beijing Jiaotong University,Beijing 100044,China)
†(Department of Mechanical Engineering,Shijiazhuang Railway Institute,Shijiazhuang 050043,China)
This paper presents the optimal design of a tunable nonlinear absorber.A nonlinear dynamic model is established based on the Hamilton principle of the minimum potential energy.The response equation of the two-DOF(degree of freedom)tunable nonlinear absorber is solved by the average method and the stability of the system is analyzed.,It is shown that with the optimized parameters,the amplitude of the vibration is reduced.
tunable,nonlinear,stability,optimization
O322
A
10.6052/1000-0879-16-241
2016–07–20收到第1稿,2016–10–11收到修改稿.
1)国家自然科学基金(50625518)和教育部科学技术研究重点资助项目.
杨柳,杨绍普,杨月婷.两自由度可调非线性减振器.力学与实践,2017,39(2):175-179 Yang Liu,Yang Shaopu,Yang Yueting.2-D tunable nonlinear absorber.Mechanics in Engineering,2017,39(2): 175-179
