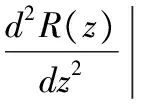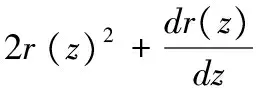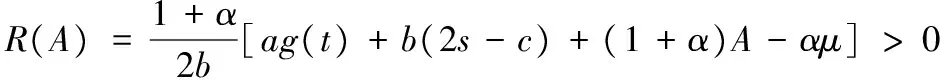考虑损失规避的温度敏感型产品定价与订货联合决策
2017-05-03曹兵兵樊治平尤天慧
曹兵兵,樊治平,尤天慧,李 琪
(东北大学工商管理学院,辽宁 沈阳 110167)
考虑损失规避的温度敏感型产品定价与订货联合决策
曹兵兵,樊治平,尤天慧,李 琪
(东北大学工商管理学院,辽宁 沈阳 110167)
在现实中存在一类温度敏感型产品,其市场需求往往与销售季内的平均温度相关。在针对温度敏感型产品的定价与订货联合决策中,温度的不确定性与零售商的损失规避行为是不可忽视的重要因素,如何构建考虑零售商损失规避的温度敏感型产品定价与订货联合决策模型是需要关注的问题。依据该类产品对温度的敏感类型,本文主要关注高温适用型和低温适用型两类产品。考虑温度变化对两类温度敏感型产品市场需求的影响,给出了两类温度敏感型产品的需求函数;在此基础上,考虑零售商的损失规避行为对零售商效用的影响,构建了以零售商期望效用最大为目标的决策模型;进一步地,依据期望效用最大化理论,求解模型并确定了零售商的最优价格和最优订货量;通过数值实验,分别针对高温适用型和低温适用型两类产品,分析了不同温度敏感系数下销售季内平均温度和损失规避系数对零售商最优决策结果的影响。分析结果表明,销售季内平均温度和零售商的损失规避程度均在不同程度上影响其最优决策结果;相对于不考虑产品温度敏感性的温度敏感型产品零售商的最优决策结果,考虑温度敏感性的该类产品零售商的最优决策结果会更加保守;分析结果还表明,考虑损失规避行为的温度敏感型产品零售商的订货量往往会高于损失中性的该类产品零售商的订货量。
报童;定价与订货联合决策;温度敏感型产品;损失规避
1 引言
现实中,存在一些温度敏感型产品,其市场需求往往会受到销售季内温度变化的影响[1]。例如,2004年欧洲夏季温度偏低,吉百利公司夏季消暑饮料销量明显下降;2005年全球多数地区温度普遍低于正常水平,沃尔玛一些特殊产品的库存积压明显增加;2006年美国东北地区温度偏高,保暖产品的销量严重下降;此外,一些历史统计数据还显示,冬季保暖衣物销售量与冬季平均温度的相关度达到91%[1]。因此,在针对温度敏感型产品的决策中销售季内的温度是不可忽视的重要因素,然而关于考虑温度因素的温度敏感型产品决策问题的研究还不多见。
本文着重分析销售季内平均温度对温度敏感型产品零售商决策的影响,并依据Fu Hongyong等[1],Whitin[2]和Petruzzi等[3]提出一种针对温度敏感型产品的定价与订货联合决策问题,其是指在市场需求随零售价格和销售季内平均温度的波动而发生变化的情形下零售商如何确定零售价格和订货量来实现最大收益的决策问题。目前,针对该决策问题可以看到一些相关的研究成果[1,4-11],例如,Fu Hongyong等[1]通过历史数据统计分析发现销售季内平均温度能够影响季节性产品的市场需求,并针对销售季内平均温度高于或低于阈值温度的情形,分别构建了定价与订货联合决策模型;Chen和Yano[4]研究了需求不确定情形下的天气敏感型产品供应链的绩效和风险管理问题,指出零售商可以通过鼓励消费者在销售季开始前购买产品来提升供应链绩效并降低风险;Aviv和Pazgal[6]将消费者的策略行为引入到季节性产品的定价问题分析中,针对可变折扣与固定折扣两种情形构建了博弈分析模型;Gao Fei等[9]分析发现季节性产品需求会随天气状态的变化而变化,并指出鼓励消费者在销售季开始前购买产品能够有效地提升季节性产品的市场需求;张宗益等[12]针对受季节性影响的天然气期货定价问题,提出了在不完全市场下的期货定价模型。
虽然针对温度敏感型产品的相关研究可以看到一些成果,但是这些成果大多是建立在完全理性假设基础上,即认为零售商是具有稳定的偏好和理性决策的能力且是为实现自身利益最大化的决策个体[13],然而,一些学者通过研究发现,在实际的决策过程中,零售商的决策结果往往会偏离完全理性下的决策结果,但通常与有限理性下的决策结果一致,并在其决策过程中表现出一些心理行为[14-15],如一些零售商会因其实际收益与其预期收益之间的差异而表现出损失规避的行为,其决策结果往往与考虑损失规避行为的决策结果是一致的[16-18]。因此,在决策过程中,应该考虑零售商的行为因素,本文侧重于研究零售商的损失规避行为。
目前,针对考虑零售商损失规避行为的定价与订货联合决策问题可以看到一些研究成果[16-25],例如,周永务等[16]分析了零售商损失规避行为对其订货与广告费用联合决策结果的影响,并构建了基于前景理论的订货与广告联合决策模型;Wang和Webster[17-18]构建了考虑零售商损失规避行为的报童决策模型,并指出损失规避型零售商的最优订货量与风险中性零售商的最优订货量之间存在明显差异;刘咏梅等[19]分析了零售商的实际决策结果偏离完全理性决策结果的原因,并指出考虑零售商损失规避等行为因素的决策结果相对于完全理性的决策结果更接近实际决策结果;Ma Lijun等[20]将损失规避行为引入到时尚产品订货问题分析中,构建了考虑损失规避行为的时尚产品供应链二次订货决策模型;文平[21]将前景理论引入到报童问题研究中,构建了考虑损失规避行为的报童决策模型,并指出零售商的损失规避行为能够影响其最优决策结果。周艳菊等[22]研究了考虑零售商行为因素的两产品订货问题,并依据前景理论构建了需求不确定情形下的两产品订货模型。丁小东等[23]分析了损失规避与浪费规避行为,并解释了零售商实际订货量与理论上最优订货量存在偏差的原因。张桂涛等[24]将损失规避行为引入到多期多产品供应链网络均衡分析中,并给出了一种具有凹性效用特征的均衡分析模型。张鹏等[25]分析了损失规避行为对零售商决策的影响,并构建了针对加性和乘性两种需求情形的定价与订货联合决策模型。
需要指出的是,虽然针对考虑零售商损失规避行为的产品定价与订货联合决策问题已经取得了一些研究成果,但是这些研究大多没有考虑温度变化对市场需求的影响,以及因温度变化而表现出的损失规避行为对零售商效用的影响。然而,在现实中,温度敏感型产品(例如,电热毯等冬季保暖产品或冷饮等夏季消暑饮品)的市场需求往往与销售季内的平均温度直接相关,且呈现出一定的不确定性,温度敏感型产品零售商针对需求的不确定性往往会表现出损失规避行为。显然,已有多数研究成果并不适用于指导温度敏感型产品零售商的决策与管理实践。因此,研究考虑零售商损失规避行为的温度敏感型产品定价与订货联合决策问题是具有理论与现实意义的。基于此,本文给出一种考虑零售商损失规避行为的温度敏感型产品定价与订货联合决策方法。
2 问题描述与符号说明
考虑单周期单一产品的定价与订货联合决策问题,零售商只有一次订货机会,且需要在销售季开始前确定其订货量,供应商具有足够的供应能力,且在销售季开始前提供所需产品。零售商的单位产品采购成本往往低于其零售价格,但高于其单位剩余产品的残值。针对温度敏感型产品,其市场需求不仅与零售价格相关,还往往与温度相关。针对高温适用型产品,温度越高,市场需求往往越高;针对低温适用型产品,温度越低,市场需求往往越高。因此,在零售商的定价与订货联合决策中,考虑市场需求为零售价格的单调减函数,温度的单调函数,且受需求随机调节因子的影响。由于现实中高温适用型和低温适用型产品较为常见,因此,本文着重分析并给出针对这两种类型产品的温度敏感型需求函数。在定价与订货联合决策中,由于温度的不确定性和需求随机因子的影响,市场需求具有明显的不确定性,致使零售商承担较大的发生缺货损失或剩余损失的风险,而面对这些风险,零售商往往会表现出一些能够影响决策的心理行为。本文侧重于研究零售商的损失规避行为对其最优决策结果的影响,即:当实际收益低于预期收益时,零售商针对感知损失而表现出的规避行为对其最优决策结果的影响。
本文需要解决的问题是,在考虑零售商损失规避行为的情形下,研究如何构建温度敏感型产品的需求函数和零售商定价与订货联合决策模型,如何确定零售商的最优零售价格与最优订货量,以及分析温度、温度敏感系数与损失规避系数对零售商最优决策结果的影响。决策问题所涉及的数学符号及其说明,如表1所示。

表1 符号说明
3 模型的构建
考虑到温度敏感型产品的市场需求不仅受到产品零售价格的影响,还受到销售季内平均温度的影响,且呈现出一定的随机性,因此,考虑温度敏感型产品的市场需求函数为:
D=ag(t)-bp+ε
(1)
其中,a为产品的市场规模,a>0;b为价格弹性,b>0;g(t)为温度敏感函数,用于描述销售季内平均温度的变化对产品市场需求的影响。考虑到销售季内平均温度变化对不同温度敏感类型产品市场需求影响是不同的,本文针对现实中较为常见的高温适用型产品和低温适用型产品,给出两种温度敏感函数,高温适用型产品的温度敏感函数为:
(2)
低温适用型产品的温度敏感函数为:
(3)
其中,TA和TB为产品的市场生存温度的下限和上限;λ为温度敏感系数,λ>0。当λ∈(0,1)、λ=1或λ>1时,产品需求随销售季内平均温度变化呈现出不同的变化趋势,如图1和图2所示。
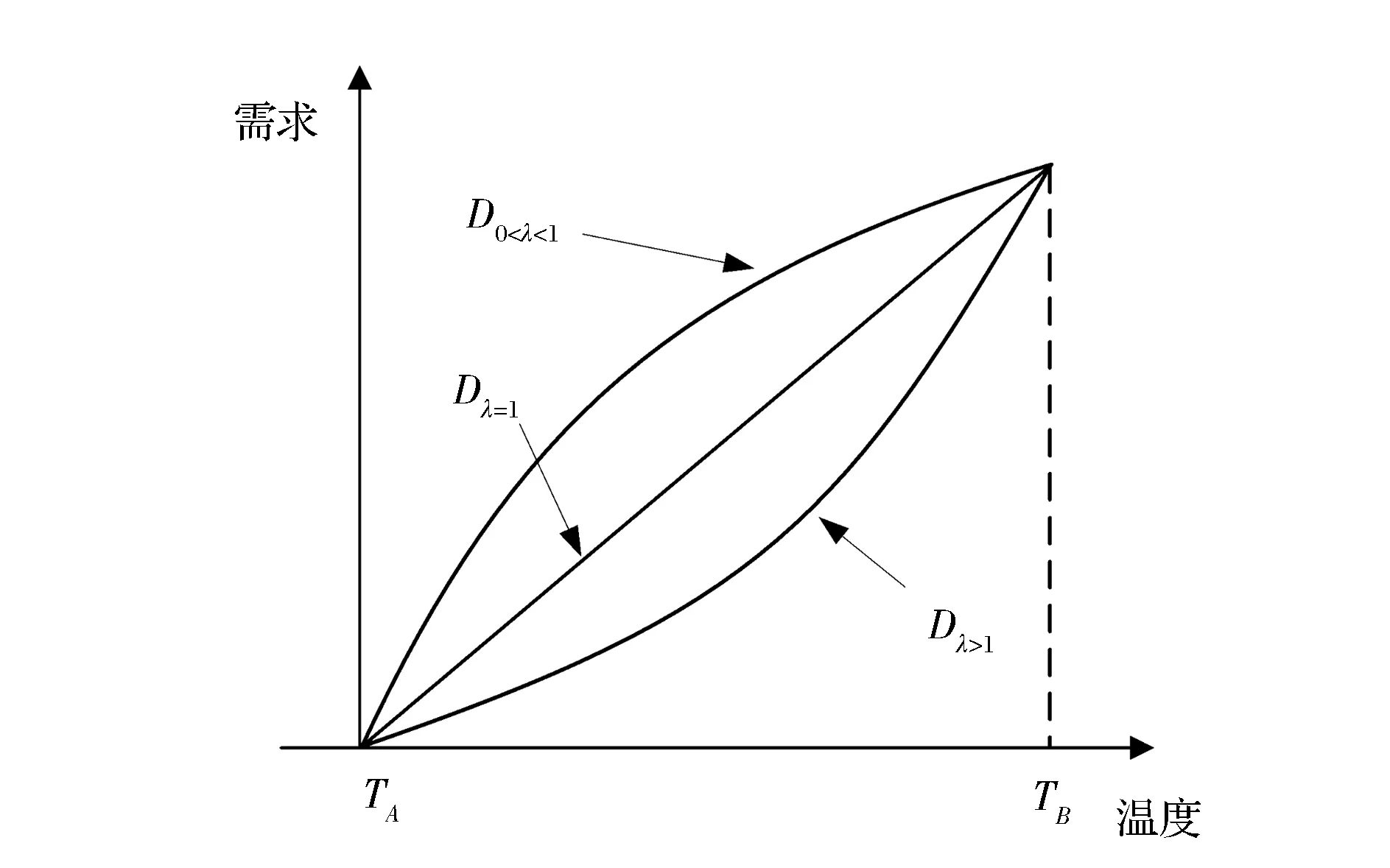
图1 高温适用型产品的市场需求函数
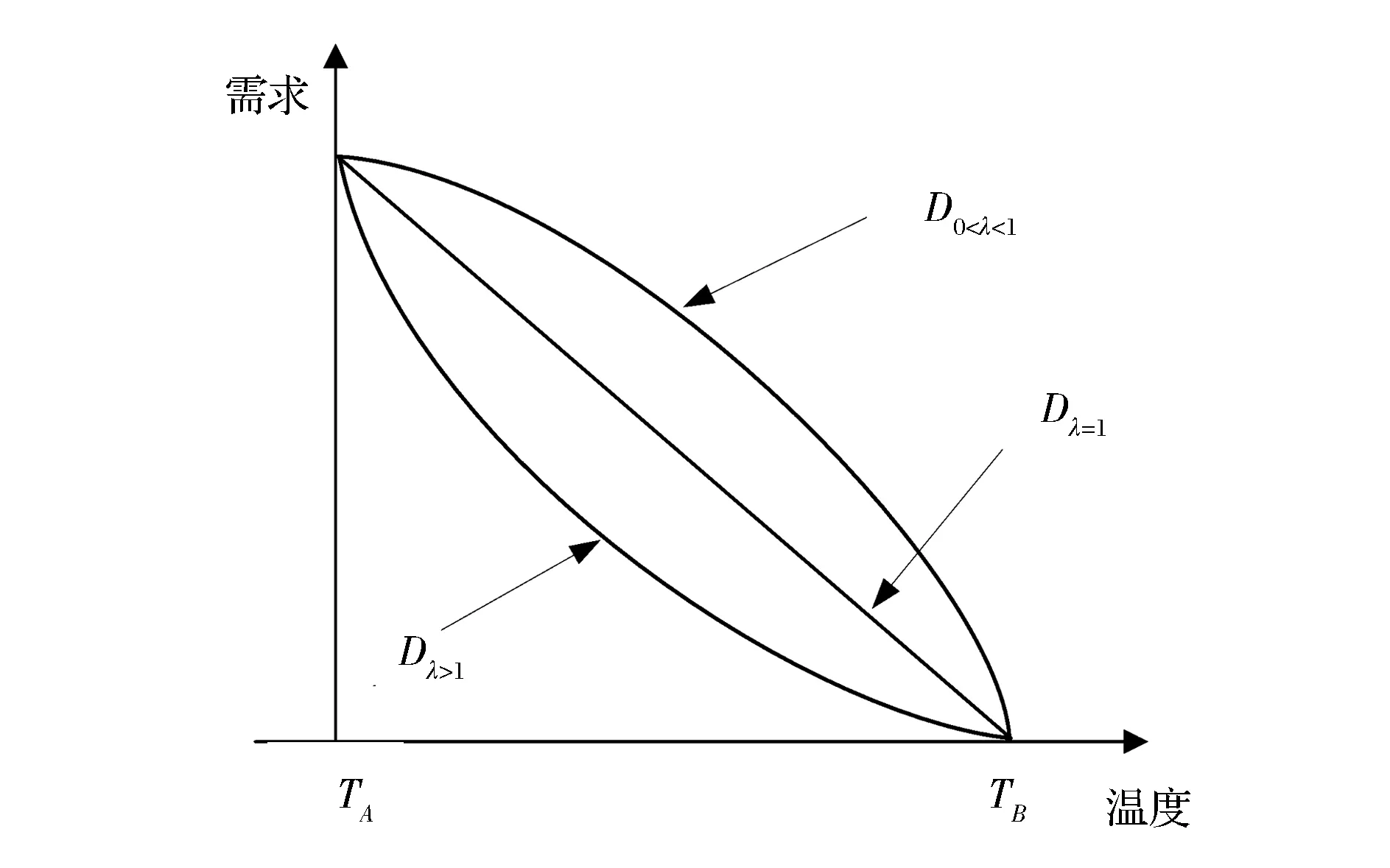
图2 低温适用型产品的市场需求函数
由图1和图2可知,高温与低温适用型产品的市场需求函数分别是温度t的单调连续增函数与减函数,且二者随温度t的变化趋势与λ的取值相关。具体地,当0<λ<1、λ=1和λ>1时,高温适用型产品和低温适用型产品的市场需求均随温度t的升高呈现出凹性敏感、线性敏感和凸性敏感趋势。
现实中,零售商往往因其实际收益低于其预期收益而感到损失,并在其定价与订货联合决策中,规避因这种感知损失而产生的负效用[16-25]。为了清晰地表述出零售商的总效用,本文采用Bell[26]以及Loomes和Sugden[27]在失望理论中给出的效用模型,其模型的形式为:
总效用(U)=经济回报(Π)+心理感知效用(ULA)
(4)
在本文中,经济回报是指零售商的利润,心理感知效用是指零售商的损失规避效用。
依据式(1)和报童模型[3],可确定零售商的利润函数为:
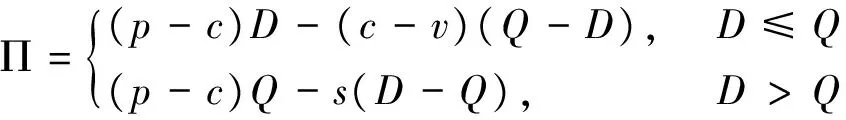
(5)
依据Wang和Webster[17],Wang[18],Bell[26]和Loomes等[27]的思想,考虑零售商的损失规避效用函数为ULA=-α(Π0-Π)+,其中,(x)+表示max(x,0);Π0为零售商的心理预期收益,其往往被视为零售商感知损失的参考点;α为零售商的损失规避系数,α≥0。α越大,零售商的损失规避程度越高。由式(5)可知,零售商在定价与订货联合决策中的最大收益为Πmax=(p-c)D,由于零售商的预期收益一般不会超出Πmax,且往往是非负的,因此,考虑零售商的预期收益Π0一般在0与Πmax之间,即Π0∈[0,Πmax][17-18]。由于本文着重分析零售商的损失规避行为对决策的影响,且当Π0=Πmax时,零售商一定会且仅会感知到损失,因此,考虑Π0=Πmax。基于此,本文考虑零售商的损失规避效用函数为:
ULA=-α(Πmax-Π)+=-α(Πmax-Π)
(6)
依据式(4)、式(5)和式(6)可知,零售商的效用函数为:
U=Π+ULA=Π-α(Πmax-Π)
(7)
式(7)即为本文所构建的考虑零售商损失规避行为的温度敏感型产品定价与订货联合决策模型。
需要指出的是,本文考虑的损失规避效应与Wang和Webster[17]和Wang[18]考虑的损失规避效应均是通过损失规避系数和参考点影响零售商最优决策的,但二者之间存在一些差异。由于二者在损失规避系数的选取上并无本质区别,因此,二者之间的差异主要表现在参考点。本文考虑损失规避效应的零售商效用可被描述为实际收益与损失规避效用之和,即U=Π+α(Π-Π0)-,Wang和Webster[17]和Wang[18]考虑损失规避效应的零售商效用可被描述为感知收益与感知损失之和,即U=Π-Π0+(λ-1)(Π-Π0)-,若参考点Π0是确定的,则二者对零售商最优决策结果的影响在整体趋势上并无本质差异;若参考点Π0是变化的(例如,Π0=Πmax),二者对零售商决策的影响在整体趋势上是存在区别的,即Wang和Webster[17]和Wang[18]考虑的损失规避效应更关注参考点Π0对零售商决策的影响。
4 模型的求解
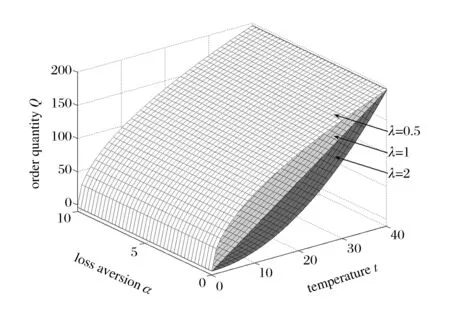
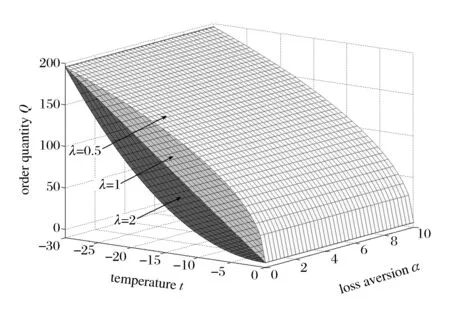
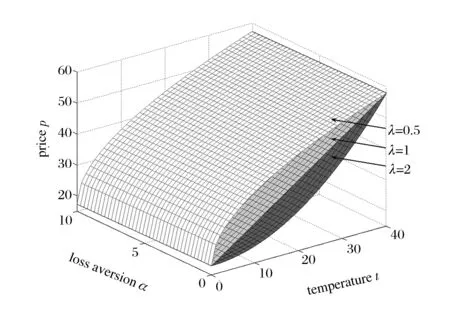
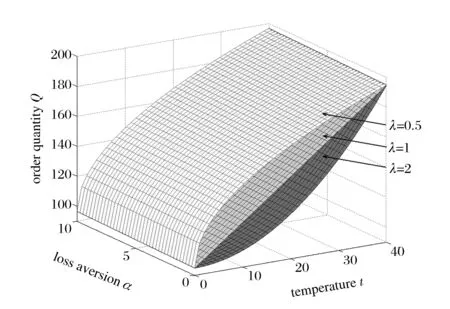
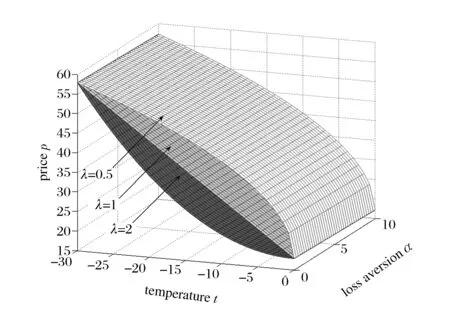
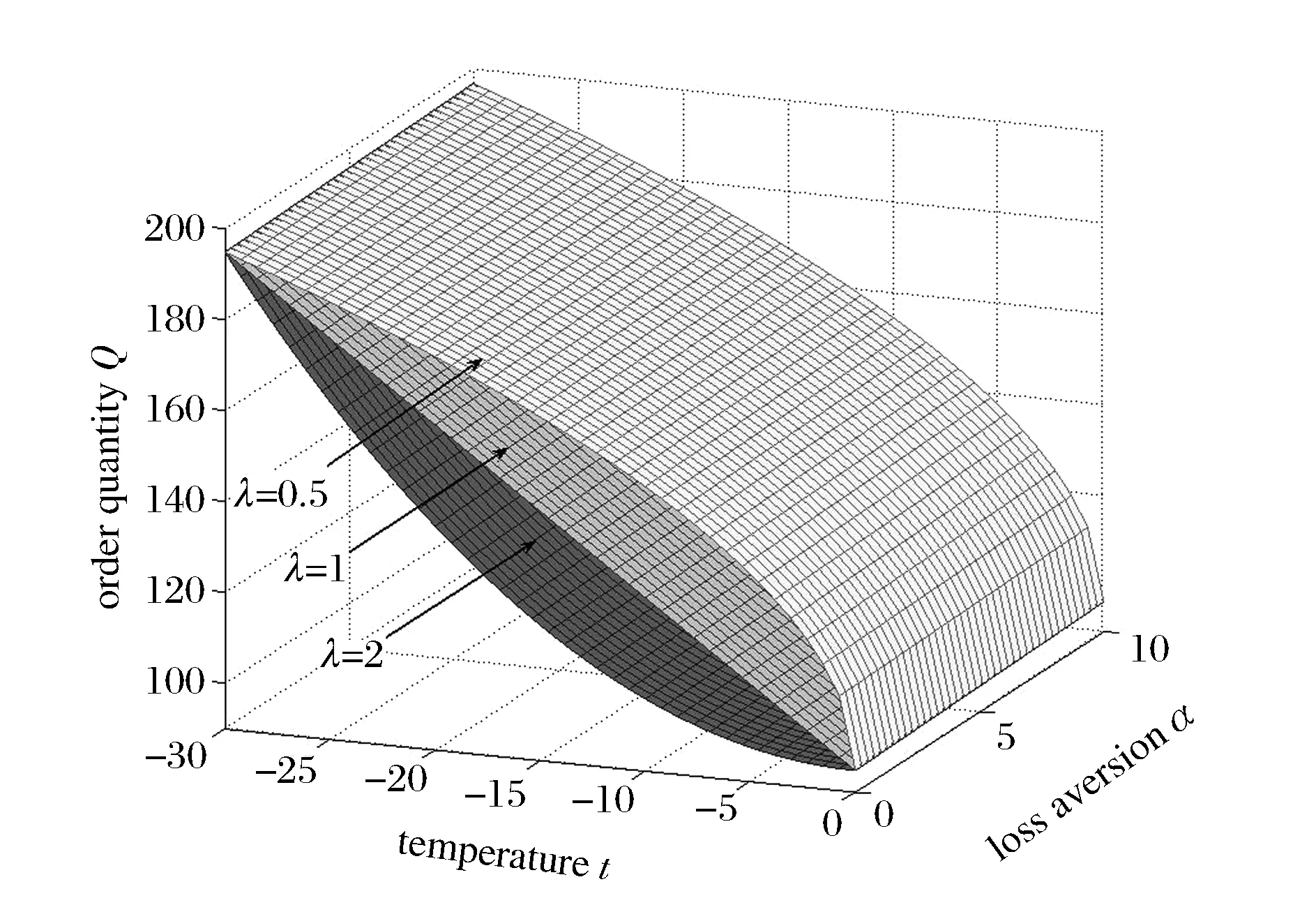
为了求解方便,这里定义订货因子z=Q-ag(t)+bp,由此可知Q=ag(t)-bp+z,则D≥Q可转化为ε≥z,D Π= (8) 依据式(7)、式(8)和Πmax=(p-c)D,可知零售商的期望效用函数,即: (9) E(U)=(p-c)[ag(t)-bp+μ]-(1+α)(c-v)Λ(z)-(1+α)(p-c+s)Θ(z) (10) 依据式(10),可知E(U)针对p和z的一阶偏导数和二阶偏导数分别为: (11) (12) (13) (14) 引理1 对于一个给定的z,最优零售价格p是唯一确定的。 (15) 证毕。 (16) 定理1 在温度敏感型产品定价与订货联合决策中,若零售商最优零售价格p*与最优订货量Q*存在Q*=ag(t)-bp*+z*的关系,且最优零售价格p*满足式(15),则可根据如下方式确定z*,进而确定最优订货量Q*: (a)若F(·)是任意累积分布函数,首先在[A,B]上任意选取z,然后依据式(15)可确定p,进而确定E(U),进一步地,在[A,B]上采用穷举z的方式可确定使零售商总体效用E(U)最大的z*和p*,并由式Q*=ag(t)-bp*+z*可确定Q*; (b)若F(·)为某一累积分布函数,且满足2r(z)2+dr(z)/dz>0,其中r(z)≡f(·)/[1-F(·)],z∈[A,B],则最优的z*为满足dE[Π(z,p(z))]/dz=0的最大z值,然后依据式(15)可确定p*,并由式Q*=ag(t)-bp*+z*可确定Q*; (c)在情形(b)成立的基础上,若ag(t)+b(2s-c)+(1+α)A-αμ>0,那么z在[A,B]内存在唯一最优解,且z*值满足dE[U(z,p(z))]/dz=0,然后依据式(15)可确定p*,并由式Q*=ag(t)-bp*+z*可确定Q*。 情形(b)和(c)的证明详见附录1。 依据上述分析,有如下命题: 命题1 针对高温适用型产品,若零售商的零售价格p是外生的,那么零售商的最优订货量Q*与其损失规避系数α无关,但与销售季内平均温度t相关,且随销售季内平均温度t的升高而增大。 证明:依据式(2)和Q*=ag(t)-bp*+z*,可知: (17) 由于p是外生的,依据式(16)可知,z是确定的;依据式(17)可知,零售商的最优订货量Q*与其损失规避系数α无关,同时,还可知: (18) 命题2 针对低温适用型产品,若零售商的零售价格p是外生的,那么零售商的最优订货量Q*与其损失规避系数α无关,但与销售季内平均温度t相关,且随销售季内平均温度t的升高而减小。 证明:依据式(3)和Q*=ag(t)-bp*+z*,可知: (19) 由于p是外生的,依据式(16)可知,z是确定的;依据式(19)可知,零售商的最优订货量Q*与其损失规避系数α无关,同时,还可知: (20) 命题3 针对高温适用型产品,若零售商的订货因子z是外生的,那么零售商的最优零售价格p*随其损失规避系数α的增大而降低,随销售季内平均温度t的升高而升高,零售商的最优订货量Q*随其损失规避系数α的增大而增大,随销售季内平均温度t的升高而增大。 证明:由于订货因子z是外生的,依据式(15)可知: (21) (22) (23) 由式(23)可知: (24) (25) 命题4 针对低温适用型产品,若零售商的订货因子z是外生的,那么零售商的最优零售价格p*随其损失规避系数α的增大而降低,且随销售季内平均温度t的升高而降低,零售商的最优订货量Q*随其损失规避系数α的增大而增大,随销售季内平均温度t的升高而减小。 证明:由于订货因子z是外生的,依据式(15)可知: (26) (27) (28) 由式(28)可知: (29) (30) 现实中,针对电热毯(低温适用型产品)或冷饮品(高温适用型产品),若零售价格外生,零售商只需要决定订货量。由于损失规避系数只能通过零售价格间接影响订货量,所以损失规避效应将无法传导到订货量,因此,电热毯或冷饮品零售商的订货量不会受到损失规避行为的影响。若订货因子外生,零售商需要决定电热毯或冷饮品的零售价格和订货量。由于损失规避系数是通过零售价格与订货因子间接相关的,且此相关性并不影响损失规避行为与零售价格之间的直接相关性,所以当订货因子确定时,损失规避系数仍然能够直接影响零售价格,并通过零售价格间接影响订货量。两种情形之间的差异主要是因为损失规避系数与零售价格、订货因子和订货量之间的相关性不同。如果损失规避系数与零售价格和订货因子均是直接相关的,那么两种情形之间将不会表现出当前的差异。 下面针对上述两种情形和三组温度敏感系数的取值以及选取的其他参数值,给出具体的数值分析。 (1) 当价格p外生时,分析系数α和温度t对最优订货量Q*的影响 依据式(2)、式(16)和Q=ag(t)-bp+z,可分别确定零售商针对三种温度敏感情形(λ=0.5、λ=1和λ=2)高温适用型产品或低温适用型产品的最优订货量Q*,经整理分析,最优订货量Q*针对损失规避系数α和销售季内平均温度t的变化趋势分别如图3和图4所示。 由图3可以看出,高温适用型产品零售商的最优订货量Q*随销售季内平均温度t的升高而增大,但与零售商的损失规避系数无关。由此可知,销售季内平均温度能够影响高温适用型产品零售商的最优订货量,且针对具有不同温度敏感程度的高温适用型产品,其影响趋势不同。由图4可以看出,低温适用型产品零售商的最优订货量Q*随销售季内平均温度t的升高而减小,但与零售商的损失规避系数无关。由此可知,销售季内平均温度能够影响低温适用型产品零售商的最优订货量,且针对具有不同温度敏感程度的低温适用型产品,其影响趋势不同。 图3 当价格p外生时,系数α和温度t对 高温适用型产品零售商最优订货量Q*的影响 图4 当价格p外生时,系数α和温度t 对低温适用型产品零售商最优订货量Q*的影响 由图3和图4可以看出,若零售价格是外生的,零售商的最优订货量往往因销售季内平均温度的变化而变化,且同一零售商针对不同温度适用类型产品以及同一温度适用型不同产品的订货策略也存在差异,同时还可知,针对温度敏感型产品,考虑产品温度敏感性的零售商的最优策略往往更加保守。 (2) 当订货因子z确定时,分析系数α和温度t对最优零售价格p*和最优订货量Q*的影响 依据式(2)、式(15)和Q=ag(t)-bp+z,可分别确定零售商针对三种温度敏感情形(λ=0.5、λ=1和λ=2)的高温适用型产品和低温适用型产品最优零售价格p*与最优订货量Q*,经整理分析,最优零售价格p*与最优订货量Q*针对损失规避系数α和销售季内平均温度t的变化趋势分别如图5、图6、图7和图8所示。 图5 当订货因子z确定时,系数α和温度t对 高温适用型产品零售商最优零售价格p*的影响 由图5可以看出,高温适用型产品零售商的最优零售价格p*随销售季内平均温度t的升高而升高,但随其损失规避系数的增大而降低,其在零售商损失规避程度最低且销售季内平均温度最高处取得最大值。由此可知,销售季内平均温度和零售商的损失规避行为能够影响高温适用型产品零售商的最优零售价格,且针对具有不同温度敏感程度的高温适用型产品,其影响趋势不同。由图6可以看出,高温适用型产品零售商的最优订货量Q*随销售季内平均温度t的升高而升高,且随其损失规避系数的增大而升高,其在零售商损失规避程度最高且销售季内平均温度最高处取得最大值。显然,销售季内平均温度和零售商的损失规避行为能够影响高温适用型产品零售商的最优订货量,且针对具有不同温度敏感程度的高温适用型产品,其影响趋势不同。 图6 当订货因子z确定时,系数α和温度t 对高温适用型产品零售商最优订货量Q*的影响 由图7可以看出,低温适用型产品零售商的最优零售价格p*随销售季内平均温度t的升高而降低,且随其损失规避系数的增大而降低,其在零售商损失规避程度最低且销售季内平均温度最低处取得最大值。由此可知,销售季内平均温度和零售商的损失规避行为能够影响低温适用型产品零售商的最优零售价格,且针对具有不同温度敏感程度的低温适用型产品,其影响趋势不同。由图8可以看出,低温适用型产品零售商的最优订货量Q*随销售季内平均温度t的升高而减小,且随其损失规避系数的增大而增大,其在零售商损失规避程度最高且销售季内平均温度最低处取得最大值。由此可知,销售季内平均温度和零售商的损失规避行为能够影响低温适用型产品零售商的最优订货量,且针对具有不同温度敏感程度的低温适用型产品,其影响趋势不同。 图7 当订货因子z确定时,系数α和温度t 对低温适用型产品零售商最优零售价格p*的影响 图8 当订货因子z确定时,系数α和温度t 对低温适用型产品零售商最优订货量Q*的影响 通过上述分析可以看出,销售季内平均温度和零售商的损失规避行为能够影响零售商的最优决策结果,且针对具有不同损失规避程度的零售商,其最优零售价格与最优订货量往往不同,针对具有不同平均温度的销售季,同一零售商的最优零售价格与最优订货量也会存在差异。此外,还可以看出,考虑产品温度敏感性的温度敏感型产品零售商最优策略相对于其不考虑产品温度敏感性的最优策略更加保守。 本文针对温度敏感型产品构建了考虑零售商损失规避行为的定价与订货联合决策模型,基于该模型可确定零售商针对高温适用型产品和低温适用型产品的最优零售价格和最优订货量,同时还给出损失规避系数和销售季内平均温度对零售商最优决策结果影响的数值分析。研究结果表明,损失规避行为与销售季内平均温度均会影响零售商的最优策略,但在影响程度和趋势上存在差异。研究结果还表明,考虑产品温度敏感性的温度敏感型产品零售商最优策略往往更加保守。基于本文研究成果,可以得到以下管理启示:销售季内平均温度的变化会影响温度敏感型产品的市场需求,针对不同温度适用型产品,其对市场需求的影响是不同的;相对于不考虑产品温度敏感性的温度敏感型产品零售商的最优决策结果,考虑温度敏感性的该类产品零售商的最优决策结果会更加保守;考虑损失规避行为的温度敏感型产品零售商的订货量往往会高于损失中性的该类产品零售商的订货量。 附录1: 定理1 (b)的证明: 从引理1可知: (A1) 为了确定满足一阶最优条件的z的值,设R(z)=dE[U(z,p(z))]/dz,考虑找到R(z)为0的点。 (A2) 记r(z)≡f(·)/[1-F(·)],则有 (A3) (A4) 定理1 (c)的证明: [1]FuHongyong,DanBin,SunXiangkai.Jointoptimalpricingandorderingdecisionsforseasonalproductswithweather-sensitivedemand[J].DiscreteDynamicsinNatureandSociety, 2014, 2014(4): 1-8. [2]WhitinTM.Inventorycontrolandpricetheory[J].ManagementScience, 1955, 2(1): 61-68. [3]PetruzziNC,DadaM.Pricingandthenewsvendorproblem:Areviewwithextensions[J].OperationsResearch, 1999, 47(2): 183-194. [4]ChenFY,YanoCA.Improvingsupplychainperformanceandmanagingriskunderweather-relateddemanduncertainty[J].ManagementScience, 2010, 56(8): 1380-1397. [5] 蔡建湖, 王丽萍. 季节性商品两级供应链契约设计与协调模型研究综述[J]. 计算机集成制造系统, 2010, 16(5): 1012-1019. [6]AvivY,PazgalA.Optimalpricingofseasonalproductsinthepresenceofforward-lookingconsumers[J].Manufacturing&ServiceOperationsManagement, 2008, 10(3): 339-359. [7]CaroF,GallienJ.Dynamicassortmentwithdemandlearningforseasonalconsumergoods[J].ManagementScience, 2007, 53(2): 276-292. [8]SoysalGP,KrishnamurthiL.Demanddynamicsintheseasonalgoodsindustry:Anempiricalanalysis[J].MarketingScience, 2012, 31(2): 293-316. [9]GaoFei,DemiragOC,ChenFY.Earlysalesofseasonalproductswithweather-conditionalrebates[J].ProductionandOperationsManagement, 2012, 21(4): 778-794. [10] 吴燕, 杨志林. 量折扣下季节性商品销售的newsboy模型[J]. 合肥工业大学学报(自然科学版), 2013, 36(6): 760-764. [11]DemiragOC.Performanceofweather-conditionalrebatesunderdifferentriskpreferences[J].Omega, 2013, 41(6): 1053-1067. [12] 张宗益, 邢文婷, 吴胜利. 不完全市场天然气期货定价及季节性影响研究[J]. 中国管理科学, 2016, 24(6): 1-9. [13]SimonHA.Abehavioralmodelofrationalchoice[J].QuarterlyJournalofEconomics, 1955, 69(1): 99-118. [14]SuXuanming.Boundedrationalityinnewsvendormodels[J].Manufacturing&ServiceOperationsManagement, 2008, 10(4): 566-589. [15]SchweitzerME,CachonG.P.Decisionbiasinthenewsvendorproblemwithaknowndemanddistribution:experimentalevidence[J].ManagementScience, 2000, 46(3): 404-420. [16] 周永务, 肖旦, 李绩才. 损失规避零售商订货量与广告费用的联合决策[J]. 系统工程理论与实践, 2012, 32(8): 1727-1738. [17]WangCX,WebsterS.Theloss-aversenewsvendorproblem[J].Omega, 2009, 37(1): 97-105. [18]WangCX,Theloss-aversenewsvendorgame[J].InternationalJournalofProductionEconomics, 2010, 124(2): 448-452. [19] 刘咏梅, 彭民, 李立. 基于前景理论的订货问题[J]. 系统管理学报, 2010, 19(5): 481-490. [20]MALijun,ZhaoYingxue,XueWeili,etal.Loss-aversenewsvendormodelwithtwoorderingopportunitiesandmarketinformationupdating[J].InternationalJournalofProductionEconomics, 2012, 140(2): 912-921. [21] 文平. 损失厌恶的报童-预期理论下的报童问题新解[J], 中国管理科学, 2005, 13(6): 64-68. [22] 周艳菊, 应仁仁, 陈晓红, 等. 基于前景理论的两产品报童的订货模型[J]. 管理科学学报, 2013, 16(11): 17-29. [23] 丁小东, 徐菱, 蒋葛夫, 等. 考虑浪费规避偏差和损失规避偏差的零售商订购行为研究[J]. 计算机集成制造系统, 2014, 20(10): 2582-2598. [24] 张桂涛, 胡劲松, 孙浩, 等. 考虑损失规避零售商的多期多产品供应链网络均衡[J]. 中国管理科学, 2015, 23(6): 73-82. [25] 张鹏, 张杰, 马俊. 两种需求情形下损失规避零售商的最优订货-定价联合决策[J]. 控制与决策, 2015, 30(10): 1820-1827. [26]BellD.Disappointmentindecisionmakingunderuncertainty[J].OperationsResearch, 1985, 33(1): 1-27. [27]LoomesG,SugdenR.Disappointmentanddynamicconsistencyinchoiceunderuncertainty[J].ReviewofEconomicStudies, 1986, 53(2): 271-282. Joint Pricing and Ordering Decisions for the Temperature SensitiveProduct Considering the Loss Aversion CAO Bing-bing, FAN Zhi-ping, YOU Tian-hui, LI Qi (School of Business Administration, Northeastern University, Shenyang 110167, China) In reality, there are temperature sensitive products, whose demands are usually related to the average temperature in the selling season. In joint pricing and ordering decisions for temperature sensitive product, the average temperature in the selling season can affect the market demand. Since the random variation of the average temperature exacerbates the fluctuation in the demand of the temperature sensitive product, the demand uncertainty increases with the random variation of the average temperature. With respect to the demand uncertainty, the retailer usually exhibits the psychological behaviors which can affect his/her decisions. Obviously, the variation of the average temperature and the behavioral factors of the retailer are important factors and cannot be ignored in joint pricing and ordering decisions for temperature sensitive product. Hence, it is necessary to pour attention to the study on joint pricing and ordering decisions considering the temperature and behavioral effects. Given that the existing research results are difficult to be used to solve the joint pricing and ordering decision problem for the temperature sensitive product considering the temperature and behavioral effects, the objective of this paper is to provide a decision method based on the optimization model to solve this problem. In this paper, two types of the temperature sensitive products are considered: One is the high-temperature suitable product, the temperature for its survival is higher and its market demand increases with the average temperature in the selling season. The other is the low-temperature suitable demand, the temperature for its survival is lower and its market demand decreases with the average temperature in the selling season. For demand uncertainty of the two types of the products, the retailer may exhibit the loss aversion. On the basis of this, the three questions concerned in this study are presented: (1) How does the average temperature in the selling season affect the demands of the two types of the products, respectively? (2) How is the loss aversion introduced into the joint pricing and ordering decision model for the two types of the products? (3) How do the average temperature in the selling season and the loss aversion affect the retailer’s optimal price and order quantity? To answer these questions, the study is conducted by the following steps. First, the impact of the average temperature in the selling season on the market demand for the high-temperature suitable product and the low-temperature suitable product is analyzed, and the high- and low- temperature sensitive demand functions for the two types of the products are provided, respectively. Then, by analyzing the loss aversion of the retailer, the loss aversion utility is introduced into the total utility of the retailer based on the utility framework model proposed by Bell (1985), and a joint pricing and ordering decision model is constructed to maximize the retailer’s total utility. Furthermore, according to the expected utility maximization theory, the retailer’s optimal price and order quantity for the two types of the products can be obtained by solving the constructed model. Finally, the numerical study is conducted to show the impacts of the average temperature in the selling season and loss aversion parameter on the retailer’s optimal price and order quantity with respect to the different temperature sensitive parameters. The results show that the average temperature in the selling season and retailer’s loss aversion can affect the optimal policy in varying degree, and the optimal policy with consideration of the impact of the average temperature on the demand is more conservative than the one without the consideration of the impact of the average temperature on the demand. The results also show that, for the high-temperature suitable product, the order quantity of the loss-averse retailer is greater than the one of the loss-neutral retailer. newsvendor; joint pricing and ordering decisions; temperature sensitive product; loss aversion 2015-12-02; 2016-10-04 国家自然科学基金资助项目(71271049, 71571039) 樊治平(1961-), 男(汉族), 江苏镇江人, 东北大学工商管理学院, 教授, 博士生导师, 研究方向: 运作管理与决策分析等, Email: zpfan@mail.neu.edu.cn. 1003-207(2017)04-0060-10 10.16381/j.cnki.issn1003-207x.2017.04.008 C 934;F 272 A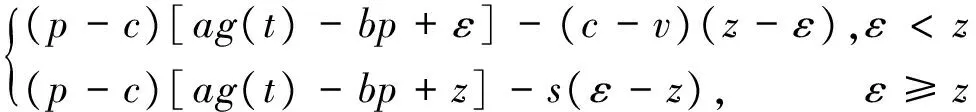
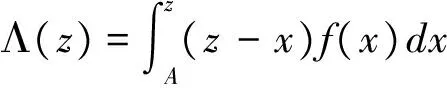
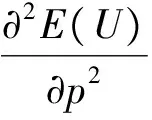
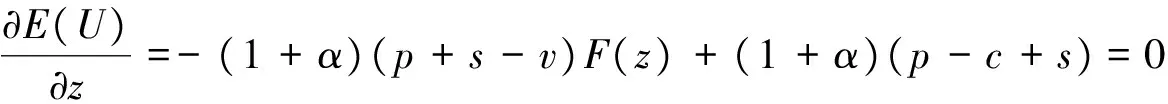
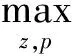
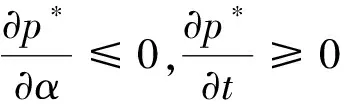
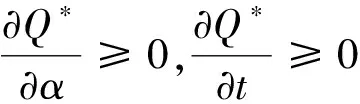
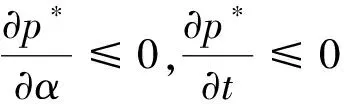
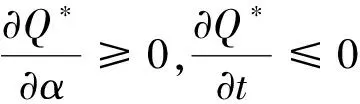
5 数值分析
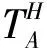
6 结语