考虑下侧风险厌恶参与者的技术外包合同研究

任 龙，刘 骏

(1.教育部人文社会科学重点研究基地清华大学现代管理研究中心，北京 100084；2.清华大学经济管理学院，北京 100084； 3.清华大学经济学研究所，北京 100084)



考虑下侧风险厌恶参与者的技术外包合同研究

任 龙1，2，刘 骏3

(1.教育部人文社会科学重点研究基地清华大学现代管理研究中心，北京 100084；2.清华大学经济管理学院，北京 100084； 3.清华大学经济学研究所，北京 100084)

本文构建了企业技术外包活动中技术需求企业与创新提供商之间的委托代理问题。由于直接面临研发风险，创新提供商为风险厌恶参与者，本文使用在险价值(Value-at-Risk)作为其风险厌恶程度的测度，并在此基础上求解最优合同参数，与传统均值—方差(M-V)效用函数的对比发现：1)随着风险波动的加剧，VaR测度下单位支付增加，而在M-V效用函数下降低；2)随着风险厌恶水平的提高，合同单位支付增加，而M-V效用函数降低；3)随着风险厌恶水平的提升，VaR下的固定支付部分也相应增加；4)VaR的两个要素对于合同的固定支付与单位支付的影响不同，保留利润水平不会影响单位支付水平，而置信水平对二者均有影响。VaR测度在克服M-V方法理论缺陷的同时，将提供更符合直觉的管理启示。

技术外包；委托代理；在险价值(Value-at-Risk)；合同设计；风险管理

1 引言

随着企业间竞争日趋激烈，产品生命周期越来越短，过去单一企业的“横向一体化”战略已经无法适应快速变化的商业环境，很多企业意识到专注于自身优势的同时，还应该同其他企业建立良好的战略同盟关系才能立于不败之地[1]。这种理念已经从生产流程延伸至研究开发环节[2]。通过研究开发业务的外包，发包企业使自身专注于核心业务，同时降低了研发成本及相关风险。自上世纪70年代以来，越来越多的公司将研发活动通过合同外包给承包者，如创意公司IDEO直接参与了苹果鼠标的设计[3]，许多科技巨头如IBM、小米等[4]，通过合理外包研发业务获得了更多的市场优势。近今年来更是兴起了专业的创新外包网站如猪八戒网(http://int.zhubajie.com/)等。

不同于传统的业务外包，研发外包活动具有极大的不确定性且信息不对称程度高，创新管理的文献大多从定性或者实证的角度对企业技术外包的动机及技术外包与传统产品外包的不同进行分析。Howells等[2]总结了技术外包与传统产品外包的不同，并以英国化工行业企业为例，通过调查的方式研究了企业技术外包的动机。Grant[5]指出企业通过研发外包可以接触到更多的技术资源，程源和雷家骕[6]认为研发外包是企业实现资源互补，进而带动产业链的重要方式，更多原因来自于企业研发创新能力的缺乏而依靠外部力量的创新活动弥补了企业的不足。

由于直接面临风险，创新业务的承包商面临较大的不确定性，故发包商与承包商之间的利润分配与风险分担问题突出。吕海萍等[7]通过实证研究发现，利益分成是研发外包的最主要障碍因素之一。如何协调技术外包中供需双方的关系，已经引起了学术界与管理者的共识。技术供需双方之间的关系可以被看作经济学中的委托代理问题，其中技术需求方为委托人，而提供创新服务的企业为代理人。信息不对称的存在使代理人的研发努力水平无法被委托人直接观察到。技术需求企业往往财力强大且并非直接面对研发风险[8]，可以视作风险中性参与者，而代理人企业如上面提到的IDEO公司由于自身力量有限且直接面临研发失败的风险，被当作风险厌恶的参与者。

学术界针对如何协调技术外包中供需双方的关系展开了大量研究，主要研究从缓解其信息不对称程度展开，按照风险来源的不同，主要分为道德风险与逆向选择问题。研究者对企业技术外包中的防范承包商或者发包商的道德风险问题进行大量研究，詹美求和潘杰义[9]对发包商与承包方之间的利益分配过程进行博弈分析，并给出了具体的参数估计方法。黄波等[10]指出当双方均存在道德风险时，传统的合约无法实现最优，他们设计了一种产出分享加固定转移支付的新混合分配方式。宋砚秋等[11]对复杂产品合作研发中的模块分包模式与联合研制模式进行研究，其说明了联合研制模式可以避免道德风险的发生，并进一步肯定了研发活动中的合作行为。高俊山等[12]在经典的契约激励合约中加入风险补偿可以降低风险成本和激励成本,从而使代理成本下降，并且该结论可以推广到任何的企业外包活动。企业技术外包中的逆向选择问题也开始引起学者的关注，刘克宁和宋华明[13]对研发外包中的逆向选择问题进行研究，其借助委托代理理论中的信息甄别模型，发包企业通过设定固定支付与线性支付对供应商的真实能力进行鉴别。在本文中对技术外包中的道德风险问题进行研究。

以上文献均使用期望效用函数或者均值方差效用函数的方式对企业的风险厌恶进行测度，但在实际中，由于创新活动的高风险性，决策者往往只关注下侧风险。如何有效得衡量创新提供商所面临的风险是本研究必须面对的问题。很多经济学与金融学的文献都对风险测度进行深入研究，如期望效用函数[14]，均值方差(M-V)效用函数[15]等。但这些风险测度的缺点都是明显的：比如期望效用函数在实际中无法真实测量导致其应用仅仅停留在理论阶段；M-V效用函数作为期望效用函数的有效近似，其应用存在一定的条件，如效用函数为二次型的形式或随机分布服从二参数分布等，这就导致其对于非对称分布无法区分上侧超额收益与下侧风险损失等，而实际中决策者往往是下侧风险厌恶的。因此M-V分析提出的同一时期，Roy[16]提出了最小化损失概率的“安全第一”标准，他将最小化破产概率引入目标函数中。他的思想被看作在险价值(Value-at-Risk)的前身。如今在险价值已经成为风险管理的新标准[17]。在险价值被定义为在某一置信水平下的最大损失，用数学符号表示为Pr{π≥VaRβ}≤1-β，其中VaR表示收益分布函数的百分位数，其将企业面临的各种风险要素映射为一个数值，简单而又直观得反映了企业在未来某段时间面临的最大损失，由于计算方便且易于实施的特点在实际中得到了广泛的运用。另一方面，本研究发现，即使使用二参数分布(正态分布)，相较于M-V效用函数，在险价值测度为创新供需双方的最优合同设计问题提供了更加符合直觉的管理启示。鉴于VaR的良好性质与广泛应用，本文将其用其来衡量代理人的风险厌恶水平。

基于此，本文试图回答如下问题：有下侧风险厌恶的创新提供商参与的技术采购问题中，最优合同的结构具有哪些特点？VaR的两个参数，即保留利润水平与风险控制水平对最优的参数有哪些影响？在本研究问题的框架下，VaR是否比M-V效用函数更能提供符合直觉的管理启示？

本文的结构安排如下，第一部分对本文的研究背景进行介绍，接着从技术外包与下侧风险测度等两个方面对文献进行回顾；第二部分介绍了模型的背景、相关定义及建立，并对最优的合同参数进行求解并进行比较静态分析；第三部分与M-V效用函数作比较；第四部分分别从风险态度与风险波动程度两方面进行数值实验，探究其对最优合同参数的影响；最后一部分对本研究进行总结，并指出未来的研究方向。

2 模型建立

2.1 问题描述与基本假设

由于无法直接观测到技术提供商的努力程度，故在技术外包的过程中存在信息不对称导致的道德风险问题。本部分对技术需求企业与提供商之间的委托代理问题建立数学模型。事件决策顺序如下：t0时刻技术需求企业提出具体的合约形式r(a,b)，根据Laffront和Martimort[18]，Laffront和Tirole[19]，当代理人为风险厌恶时，固定的价格合约与纯粹的产出分享合约并非最优，最优合约由固定支付及独立的线性支付部分组成，即r(a,b)=a+bQ，其中a为无论最终结果如何，总会获得的固定支付，b为单位支付，即每一单位产出Q所带来的支付；t1时刻技术提供商观察到合同的具体参数，决定是否参与，同时确定研发努力程度w，研发努力程度为技术提供商的私有信息；t2随机产出Q(w,ε)实现，产出水平由企业的努力程度w与随机扰动项ε决定，这里ε项表示创新产品的产出风险，在此假定Qw>0,Qww<0，即产出存在边际递减效应，最终企业根据合同的参数与产出的实际水平获得现金流入。假设φ(w)为努力成本，且φw>0,φww<0。s,f分别代表创新产品采购与销售价格，为外生变量。

2.2 模型建立

假设技术需求方为风险中性参与者，故其期望效用函数与期望利润等价，可表示为：

UG=fQ(w,ε)-r(a,b,Q(w,ε))=(f-bs)Q(w,ε)-a

技术提供商的利润函数为：

πf=r(a,b,Q(w,ε))-φ(w)=a+bsQ(w,ε)-φ(w)

IR约束表示提供商参与此合同时必须达到的保留利润水平,记IR约束的保留利润为V0。作为一个下侧风险厌恶参与者，VaR约束Pr{πf≤π0}≤β表示实现利润小于保留利润水平π0的概率小于某一阈值β，而激励相容约束(IC)表示提供商会选择努力水平w∈argmaxE[πf]来最大化。故此问题可以表示如下：

MaxE[(f-bs)Q(w,ε)-a]

s.t.E[a+bsQ(w,ε)-φ(w)]≥V0(IR)

Pr{a+bsQ(w,ε)-φ(w)≤π0}≤β(VaR)

w∈argmaxE[a+bsQ(w,ε)-φ(w)](IC)

2.3 符号说明

正如上面所介绍的，本文中使用的主要符号及意义如表1所示。

表1 主要符号说明

2.4 模型求解

为了问题的简化且不失一般性，我们假Q(w,ε)=lnw+ε,φ(w)=wθ,ε～N(0,σ),θ>1。将其带入上面的问题，我们得到：

MaxE[(f-bs)(lnw+ε)-a]

s.t.E[a+bs(lnw+ε)-wθ]≥V0(IR)

Pr{a+bs(lnw+ε)-wθ≤π0}≤β(VaR)

w∈argmaxE[a+bs(lnw+ε)-wθ](IC)

其中αβ表示正态分布的β分位数。对以上问题使用KKT条件进行求解。

根据KKT条件，有：

μ1+μ2=1

对上式进行求解，我们得到如下定理：

由上式我们可以发现，当eθf+θσαβ>1成立时，固定支付部分为关于风险波动率的增函数。通过对最优单位支付的比较静态分析我们发现，b*为关于β与σ的增函数，随着风险厌恶程度与风险波动水平的提高，最优的线性支付部分b*是增加的，但其与保留利润水平π0无关。对最优固定支付部分a*进行分析，发现其为保留利润水平π0的增函数。而a*关于风险控制水平β及风险波动程度的单调性无法确定。下面，我们将对M-V效用函数进行分析。

3 与均值—方差方法的比较

均值方差分析方法最早由Markowitz提出，在投资组合理论、风险管理等方面均得到了广泛应用，下面我们将VaR方法与传统的均值—方差分析进行比较。使用均值—方差效用函数，本问题的模型可以表示为：

MaxE[(f-bs)(lnw+ε)-a]

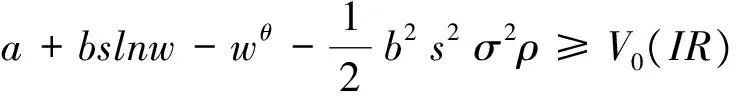
w∈argmaxE[a+bs(lnw+ε)-wθ](IC)

可以发现与VaR测度下的最优合同参数相反，随着ρ及σ的增大，最优的b*是降低的，即随着风险厌恶水平与风险波动程度的增加，最优的固定支付部分反而是降低的。我们进一步对M-V效用函数下的最优固定部分进行分析：

与VaR的结论相同，其单调性取决于参数的具体取值，仅大于0时M-V的固定支付部分为关于风险厌恶水平的增函数。

对比两种风险测度我们可以发现：理论上M-V方法有其应用的局限性，如效用函数为二次形式；随机分布为两参数分布等，而创新活动存在较大的不确定性，故二参数分布难以较好得刻画此类不确定性(如偏峰厚尾性质等)。而VaR方法并没有对分布的具体形式进行限定。

另外，在本研究中我们发现，即使使用对称分布，VaR风险厌恶者随着风险波动的加剧，其单位支付增加，而M-V风险厌恶者降低；随着风险厌恶水平的提高，VaR风险厌恶者的单位支付增加，而M-V风险厌恶者降低；随着风险厌恶水平(保留利润)的提高，VaR厌恶者的固定支付部分也当相应增加；VaR的两个参数对于合同的固定支付与单位支付的影响不同，保留利润水平不会影响单位支付水平，而风险控制水平对二者均有影响。由此可见，VaR风险厌恶者的反应更加真实。

两种风险测度下的主要结论如表2所示。

表2 不同因素对于合同参数的影响分析

4 数值算例

为了更直观得对问题进行刻画，本部分使用数值算例对不同因素对于最优合同的影响进行分析，主要考虑的因素为风险态度与需求的波动程度，即π0与β，V0与σ等。数值算例的主要参数如表3所示。

表3 数值算例基本参数

4.1 风险态度

其他参数保持不变，调整π0与β的数值时，结果如表4所示。

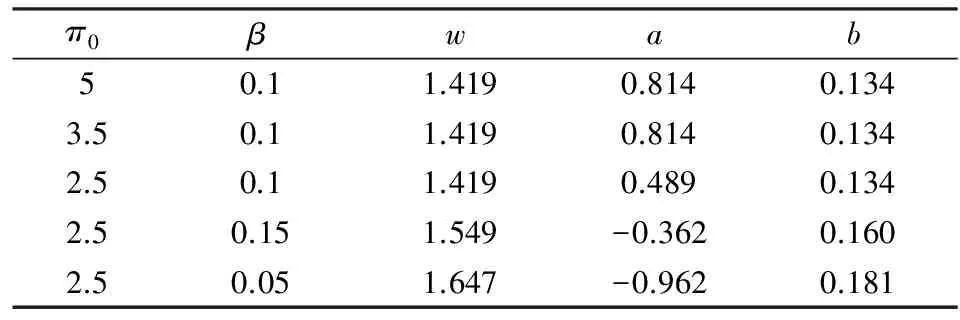
表4 π0与β对合同参数的影响

当风险控制水平不变，企业的保留利润水平增大时，其固定部分也随之增大。当保留利润水平不变，风险控制水平增大时(风险厌恶程度减小)，在此算例中显示最优的线性参数减小，而最优的固定部分增加。

4.2 波动率

另一方面，我们在其他参数不变的前提下研究了波动率对最优参数的影响，如表5所示。

表5 σ对最优合同参数的影响

当波动率变大时，表示企业面对的风险加剧，企业的最优努力水平随之提高，合同参数的单位支付也随之提高。

5 结语

技术外包在高风险的创新产品研发过程中发挥着重要作用。一方面，同一般性的企业业务相比，研发具有高度的不确定性，企业可能很难收回其投入成本，技术需求者需要提出有效的机制来补偿其风险。传统的风险测度如均值方差方法在理论上存在诸多不足，且往往获得与常理相悖的结论，如随着风险厌恶程度与风险波动水平的加剧，单位支付部分反而降低。本文从下侧风险厌恶的角度，使用金融机构中广泛采用的在险价值(Value-at-Risk)作为衡量企业下侧风险的测度，对技术外包中存在的委托代理问题进行求解。研究发现，在VaR框架下单位支付随着风险厌恶水平及风险波动程度的加剧而增加，而当使用M-V效用函数时单位支付降低；随着风险厌恶水平(保留利润)的提高，VaR下的固定支付部分也当相应增加，即其固定支付部分随着风险厌恶程度的增加而增加，而M-V效用函数并不能得出如此的结论。

另外，VaR的两个参数对于合同的固定支付与单位支付的影响不同，保留利润水平不会影响单位支付水平，而风险控制水平对二者均有影响。由此可见，使用VaR作为衡量承包者的风险厌恶测度更加符合实际。本研究从风险管理的视角对风险厌恶参与者的合同设计问题进行解释，具有很好地理论与现实意义。

本研究所建立的理论模型可以拓展到有多个技术提供商参与的情景，此时多个技术提供商之间的竞争关系将产生新的协调问题。另一个可以拓展的方向为监督成本的存在对于合同参数的影响。由于VaR约束所形成可行域的非凸性，其拓展到多周期的委托代理问题存在较大的技术困难，也不失为一种有效尝试。

[1] Coombs R. Core competencies and the strategic management of R&D[J]. R&D Management, 1996, 26(4): 345-355.

[2] Howells J, Gagliardi D, Malik K. The growth and management of R&D outsourcing: Evidence from UK pharmaceuticals[J]. R&D Management, 2008, 38(2): 205-219.

[3] Kelley T. The art of innovation: Lessons in creativity from IDEO, America's leading design firm[M]. New York:Cumency Doubleday,2001.

[4] Leimeister J M, Huber M, Bretschneider U, et al. Leveraging crowdsourcing: Activation-supporting components for IT-based ideas competition [J]. Journal of Management Information Systems, 2009, 26(1): 197-224.

[5] Grant R M. The resource-based theory of competitive advantage: Implications for strategy formulation[J]. California Management Review, 1991, 33(3): 114-135.

[6] 程源, 雷家辅. 企业技术源的演化趋势与战略要义[J]. 科学学与科学技术管理, 2004, 25(9): 74-77.

[7] 吕海萍, 龚建立, 王飞绒, 等. 产学研相结合的动力一障碍机制实证分析[J]. 研究与发展管理, 2004, 16(2): 58-62.

[8] Doctor R N, Newton D P, Pearson A. Managing uncertainty in research and development[J]. Technovation, 2001, 21(2): 79-90.

[9] 詹美求, 潘杰义. 校企合作创新利益分配问题的博弈分析[J]. 科研管理, 2008, 29(1): 8-13.

[10] 黄波, 孟卫东, 皮星. 基于双边道德风险的研发外包激励机制设计[J]. 管理工程学报, 2011, 25(2): 178-185.

[11] 宋砚秋, 贾传亮, 高天辉. 复杂产品系统合作创新契约模型有效性研究[J]. 中国管理科学， 2011，19(2): 155-160.

[12] 高俊山, 韦静, 李晓非, 等,业务外包委托代理模型中的风险补偿安排[J]. 中国管理科学, 2008, 16(5): 164-170.

[13] 刘克宁,宋华明. 不对称信息下创新产品研发外包的甄别契约设计[J]. 中国管理科学, 2014, 22(10):52-58.

[14] Von Neumann J, Morgenstern O. Theory of games and economic behavior[M]. Priceton:Princeton University Press, 2007.

[15] Markowitz H. Portfolio selection[J]. Journal of Finance, 1952, 7(1): 77-91.

[16] Roy A D. Safety first and the holding of assets[J]. Econometrica, 1952: 431-449.

[17] Jorion P. Value at risk: The new benchmark for managing financial risk[M]. New York: McGraw-Hill, 2007.

[18] Laffont J J, Martimort D. The theory of incentives: The principal-agent model[M]. Princeton:Princeton University Press, 2009.

[19] Laffont J J, Tirole J. A theory of incentives in procurement and regulation[M]. Camlridge,Massachusetts:MIT press, 1993.

Study on Enterprise Technology Outsourcing with Downside Risk Averse Agent

REN Long1，2, LIU Jun3

(1. Research Institute of Humanities and Social Sciences at Universities,Research Center for ContemporaryManayement,Tsinghua University,Beijing 100084,China;2.School of Economics and Management, Tsinghua University, Beijing 100084,China;3.Institute of Economics, Tsinghua University, Beijing 100084,China)

To acquire competitive advantages in an ever-changing business environment, many business gurus step up to outsource their non-core activities to third-party members. Except for some basic activities such as operations and marketing, R&D outsourcing has become prominent since 1970s. There are many success examples such as IDEO, an international design and consulting firm founded in California, in 1991, participating in the design of Apple Mouse. Different from other activities, R&D outsourcing is with high uncertainty and information asymmetry. The risk sharing and information issues are very important for both participants. To tackle with these problems, a principal-agent like R&D outsourcing problem between a technology provider and buyer is studied. Since the buyer can’t observe the provider’s R&D effort, an optimal contract must be designed to alleviate the moral hazard problem. The contract is composed of two parts, namely fixed payment and unit payment. Fixed payment mean no matter what the random output is, the provider will get this part. The unit payment is the gain for each unit output. Faced directly to R&D risks, the technology supplier is regarded as a downside risk averse agent. The provider’s risk aversion attitude is modeled with Value-at-Risk (VaR) constraint. By solving this optimization problem with KKT conditions, the VaR results are compared against the seminal mean-variance framework, and it is founol that: 1) the unit payment under VaRincreases as the demand volatility increases, while it decreases under M-V framework; 2) as the risk aversion increases, unit payment in VaR increases while M-V decreases; 3) as the provider becomes more risk averse, the fixed payment under VaR increases; 4) reserved profit and risk control level plays different roles in determine the optimal parameters, the reserved profit doesn’t impact on the unit payment while the risk control level influences them both. VaR method not only overcomes the shorting comings of mean-variance method in theory, such as M-V can’t separate upper gains with downside loss. The VaR method also provides much more clear managerial insights for technology outsourcing problem.

technology outsourcing; principal agent; value-at-Risk;contract desing; risk management

2016-03-12；

2016-07-07

国家自然科学基金资助项目(71232007)

任龙(1989-)，男(汉族)，山东人，清华大学经济管理学院博士研究生，研究方向：机制设计、风险管理,E-mail:lewisrenthu@gmail.com.

1003-207(2017)04-0184-06

10.16381/j.cnki.issn1003-207x.2017.04.022

F224

A