抗差自适应滤波在低轨飞行器INS/CNS/GNSS组合导航中的应用

秦 峰，宋振华，吴 镇

(上海机电工程研究所，上海 201109)



抗差自适应滤波在低轨飞行器INS/CNS/GNSS组合导航中的应用

秦 峰，宋振华，吴 镇

(上海机电工程研究所，上海 201109)

低轨飞行器对导航系统的稳定性要求较高，采用标准卡尔曼滤波的组合导航系统在异常扰动情况下会产生较大误差，严重影响低轨飞行器导航精度.在此前提下提出将抗差自适应滤波用于低轨飞行器导航系统，并基于该滤波器设计INS/CNS/GNSS组合导航.通过仿真实验对比验证抗差自适应滤波的有效性.

组合导航；自适应；抗差；卡尔曼滤波；低轨飞行器

0 引 言

单一的导航系统，往往难以全面地满足载体的导航需求，在这种背景下，组合导航系统被提出.它将两种或两种以上的非相似导航系统对同一导航参数进行测量并融合得到最优导航信息，从而提高导航系统整体性能[1].组合导航使导航结果更加全面，具有较高的短时和长时定位精度以及更好的导航完好性，可以适用于多种应用场景.

用于空间航天器的组合导航技术开展相对较晚，20世纪90年代初期，NASA支持开展的研究，验证了GPS和INS组合导航系统为航天器提供高精度位置、速度和姿态信息的可行性.为了提供完备的导航信息以满足空间转移飞行器的多种空间任务要求，需要将导航和指向敏感器如：雷达、INS、星敏感器、地平敏感器和太阳敏感器等，与GPS导航组合构成导航系统[2-3].从1999年至今，美国霍尼韦尔公司研发了先进的空间组合导航系统SIGI，系统具有为航天器提供全运行阶段(入轨、在轨、再入和着陆)的导航信息的能力[4-5].

在组合导航中，多敏感器的数据融合大多通过卡尔曼滤波实现.然而，采用传统卡尔曼滤波时，如果导航过程出现异常扰动，导航结果将受到显著影响，导致误差增大.因此，杨元喜等[6-7]提出了一种新的抗差自适应滤波理论，该理论应用抗差估计原理控制观测异常的影响，引进自适应因子控制动力学模型误差和异常扰动的影响.目前，抗差自适应滤波已在道路修测、车辆导航等多个领域实现了广泛应用[8].本文针对低轨飞行器设计了INS/CNS/GNSS组合导航系统，并将抗差自适应滤波应用于多敏感器数据融合过程，使组合导航系统具有抗异常扰动的能力，从而保证飞行器的可靠稳定导航.

1 INS/CNS/GNSS组合导航原理和结构

对于在空间飞行的低轨飞行器，单一的导航系统难以全面满足它长时稳定的导航需求，因此，本文利用惯性导航系统(inertial navigation system，INS)、天文导航系统(celestial navigation system，CNS)和全球卫星导航系统(global navigation satellite system，GNSS)相互互补的特性，构成组合导航系统实现低轨飞行器的长航时高精度导航.采用的模式为松组合，这种组合模式的优点是结构简单，无论是在硬件设计还是软件的编制和调试上，都便于在工程上实现；组合系统的计算量小，可以满足对实时性要求较高的系统设计；另外，由于两个子系统是独立工作的，所以便于容错处理.

低轨飞行器组合导航系统将惯性敏感器的测量信息、星敏感器测量信息和GNSS接收机导航输出的位置、速度相融合.系统组成主要包括：星敏感器(安装于CNS)、3个正交加速度计(安装于INS)、GNSS接收机、导航计算机及接口、通讯总线等.其中，加速度计输出载体三轴加速度信息，星敏感器输出载体姿态四元数信息，利用这些信息先进行惯导解算，解算结果再与GNSS接收机输出的位置和速度信息相融合估计出惯导误差并得到最优的导航输出[9].整个INS/CNS/GNSS组合导航的工作原理和基本结构如图1所示.

图1 低轨飞行器组合导航工作原理Fig.1 Principle of INS/CNS/GNSS integrated navigation for the LEO spacecraft

2 组合导航自适应滤波设计

在INS/CNS/GNSS组合导航系统中，组合滤波算法是整个系统实现的核心，对外输出载体的位置、速度和姿态的最优估计.由于低轨飞行器在实际动态导航过程中，难免存在建模误差和不确定的动力学模型噪声，导致卡尔曼滤波发散.因此，本文将自适应滤波方法应用于INS/CNS/GNSS组合导航滤波设计中，自适应地调整状态预测向量和观测值之间的权比，从而控制扰动异常对组合导航滤波中状态估计的影响.

2.1 系统状态方程

在INS/CNS/GNSS组合导航滤波器设计中，系统的状态变量主要选择为：位置误差、速度误差、姿态误差、加速度计零偏，整个导航过程在地心惯性坐标系(earth-center inertial，ECI)中实现.由于系统的状态方程和观测方程均为线性的，系统状态误差的估计过程是个线性滤波的过程.通常采用线性卡尔曼滤波器进行滤波估计.

低轨飞行器INS/CNS/GNSS组合导航系统卡尔曼滤波器的状态方程和状态矢量为

(1)

其中，X(t)为系统状态变量，W(t)为系统噪声，F(t)和G(t)分别为系统的状态和噪声系数矩阵.

选择ECI坐标系作为导航坐标系，列出状态变量

(2)

X(t)包含的误差状态变量如表1所示(为书写方便，略去坐标系上下标).

表1 INS/CNS/GNSS组合导航滤波误差状态变量Tab.1 Error state vectors of the INS/CNS/GNSS integrated navigation

低轨飞行器INS/CNS/GNSS组合导航系统状态量包含了位置、速度和姿态四元数误差矢量以及加速度计偏差矢量；系统噪声主要包含了加速度计噪声.通过滤波实时估计得到的惯性敏感器偏差，用于反馈校正惯性敏感器输出.其中，状态系数矩阵F(t)和噪声系数矩阵G(t)可根据文献[10-11]中惯性导航误差方程得到.

2.2 系统观测方程

低轨飞行器INS/CNS/GNSS组合导航滤波器的观测量为GNSS和INS位置和速度矢量之差.系统观测方程为：

Z(t)=H(t)X(t)+V(t)

(3)

(4)

其中，H(t)为观测系数矩阵，V(t)是观测噪声.

为了便于工程实现，在实际使用时状态方程和观测方程均需先离散化.

2.3 自适应卡尔曼滤波

运动物体一般难以确保规则运动，低轨飞行器绕地球飞行时也难以保证始终均匀的规则匀速绕动，故难以构造精确的函数模型；而载体在运动过程中，又不可避免地受到外界异常干扰的影响.为了克服卡尔曼滤波模型误差和异常扰动的影响，本文在INS/CNS/GNSS组合导航滤波器设计中采用了抗差自适应卡尔曼滤波，利用自适应因子实时调节卡尔曼滤波时预测信息和量测信息的权重，以实现状态的平滑准确估计.

(5)

(6)

(7)

其中，Pk/k-1为状态预测协方差矩阵，Rk为量测噪声方差矩阵.

基于式(6)统计量进一步构造自适应因子为

(8)

将自适应因子引入卡尔曼滤波可得到自适应卡尔曼方程为[7]

(9)

(10)

(11)

(12)

(13)

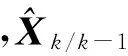
3 仿真与分析

3.1 仿真轨迹与数据生成

为了验证设计的抗差自适应滤波用于低轨飞行器组合导航的有效性，通过轨迹模拟器模拟一条绕地球飞行的低轨轨迹，轨迹如图2所示.将模拟的轨迹注入惯性敏感器数据模拟生成器和GNSS卫星导航数据模拟器，设定敏感器误差参数，生成与飞行器运动轨迹一致的惯性敏感器数据和GNSS接收机输出数据，用于INS/CNS/GNSS组合导航仿真实验.表2列出了模拟的惯性敏感器和GNSS接收机输出数据主要误差参数.

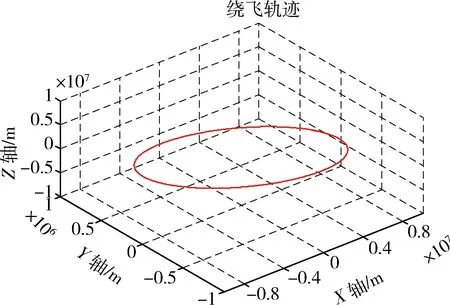
图2 低轨飞行器运动轨迹Fig.2 Trajectory of the LEO spacecraft

表2 敏感器输出数据误差参数
Tab.2 Error parameters of the sensor outputs

敏感器参数误差星敏感器姿态1″加速度计零偏5×10-5g(3σ)GNSS接收机位置10mGNSS接收机速度0.25m/s

低轨飞行器的整个运动轨迹共持续6 000 s，为了比较抗差自适应滤波和标准滤波性能，充分验证抗差自适应滤波的自适应能力和抗差效果，证明抗差自适应滤波的优势，仿真时在400～800 s、2400～3 200 s和4 400～5 000 s 3个时间段分别加入异常扰动误差，所加异常扰动为在三轴加速度上的正弦扰动，扰动模型如下：

B=0.2sin(2πωt)

(14)

其中，ω=0.5 Hz.

3.2 仿真结果

为了比较分析自适应滤波的抗差性能，本文在仿真中同时采用抗差自适应卡尔曼滤波和标准卡尔曼滤波两种方案进行组合导航实验.组合导航时惯性导航解算周期为0.4 s，组合滤波周期均为2 s，观测位置噪声为10 m，观测速度噪声为0.25 m/s.采用两种滤波的组合导航位置误差和速度误差分别如图3～4所示.

图3 两种滤波位置误差Fig.3 Position errors of two filters

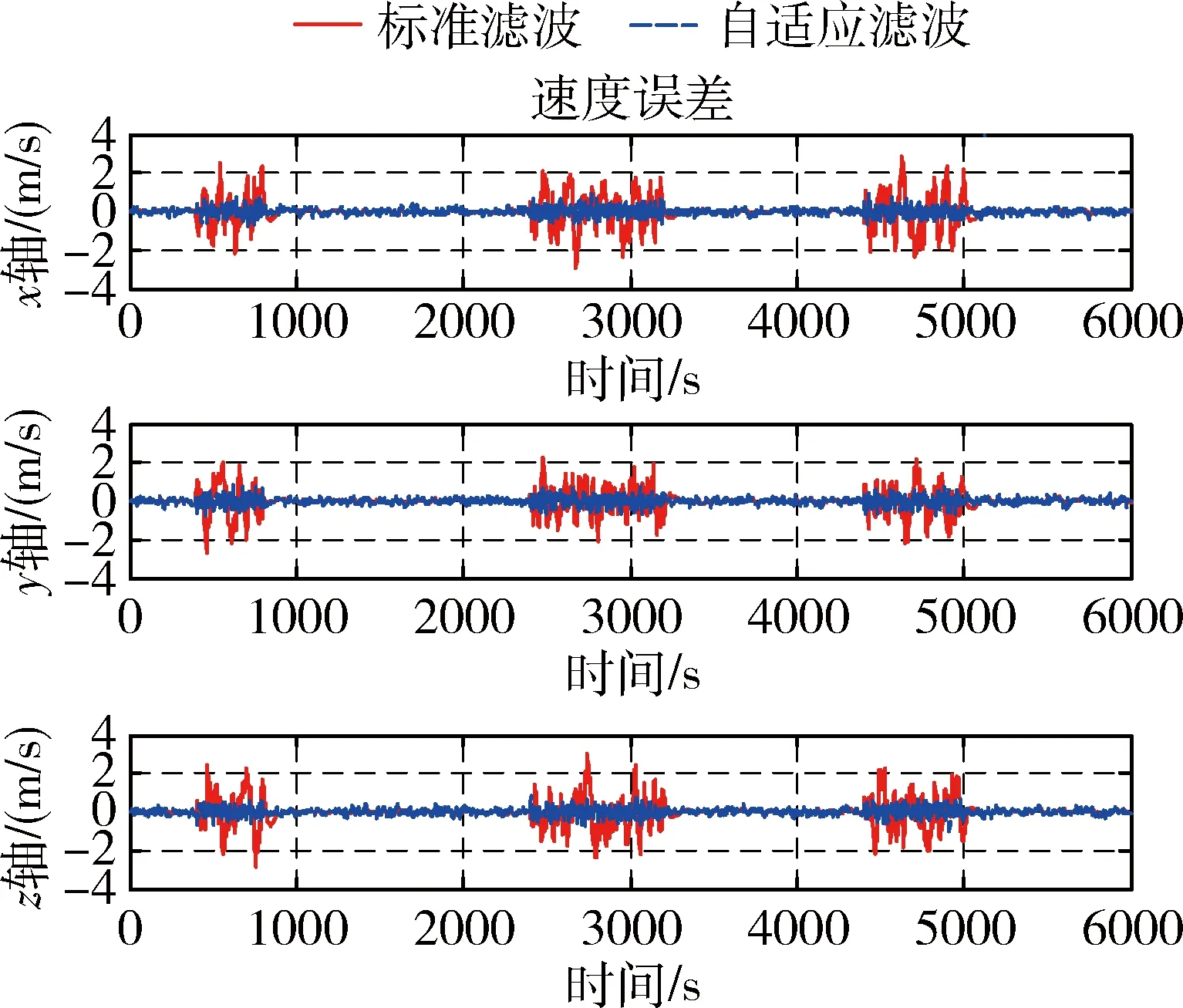
图4 两种滤波速度误差Fig.4 Velocity errors of two filters

从图中可以看出，采用标准卡尔曼滤波实现组合导航时，由于预测信息和量测信息的权重无法自适应调节，当出现异常扰动时，位置误差和速度误差明显增大，导航结果明显恶化；反之，采用自适应卡尔曼滤波实现组合导航时，由于自适应因子的存在，历史信息的使用效率降低，使异常扰动带来的影响明显得到抑制，使导航系统具有抗差能力，从而保证了组合导航的精度.表3为异常扰动发生时采用标准卡尔曼滤波和自适应卡尔曼滤波的最大导航位置误差和速度误差.

表3 两种滤波组合导航误差比较Tab.3 Errors comparison between the integrated navigations with two different filters

4 结 论

本文采用抗差自适应滤波取代标准卡尔曼滤波，用于低轨飞行器INS/CNS/GNSS组合导航，以抑制异常扰动时导航误差增大，使系统更加稳定的导航.文中具体研究了抗差自适应卡尔曼滤波算法，并基于该算法设计了组合导航系统.仿真实验结果表明，相比标准卡尔曼滤波，设计的自适应卡尔曼滤波算法在异常扰动发生时可以自适应调节预测信息和量测信息，抑制了扰动对系统的影响，使导航误差大大降低.

[1] 秦永元，张洪钺，汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社: 1998. QIN Y Y, ZHANG H Y, WANG S H.Principle of Kalman filter and integrated navigation[M]. Xi’an, Northwestern Polytechnical University Press,1998.

[2] UPADHYAY T N, COTTERILL S, DEATON A W. Autonomous GPS/INS navigation experiment for space transfer vehicle[J]. IEEE Transactions on Aerospace and Electronic System, 1993, 29(3): 772-785.

[3] HABLANI H. Autonomous inertial relative navigation with sight-line-stabilized sensors for spacecraft rendezvous[J]. Journal of Guidance, Control and Dynamics, 2009, 32(1)： 172-183.

[4] WILLMS B. Space integrated GPS/INS (SIGI) navigation system for space Shuttle[C]//Digital Avionics Systems Conference. St. Louis: 1999: 7.A.4-1-7.A.4-8.

[5] HEGG J. Enhanced space integrated GPS/INS (SIGI)[J]. Aerospace and Electronic Systems Magazine, IEEE, 2002, 17(4)： 26-33.

[6] YANG Y, HE H, XU G. Adaptively robust filtering for kinematic geodetic positioning[J]. Journal of Geodesy, 2001, 75(2-3): 109-116.

[7] 杨元喜，任夏，许艳. 自适应抗差滤波理论及应用的主要进展[J]. 导航定位学报，2013，1(1): 9-15. YANG Y X, REN X, XU Y. Progress of the principle and application ofadaptively robust filtering[J]. Journal of Navigation and Positioning, 2013, 1(1): 9-15.

[8] 吴富梅，杨元喜，田育民. GPS/DR组合导航自适应Kalman滤波算法[J]. 测绘科学技术学报，2008，25(3): 206-208. WU F M, YANG Y X, TIAN Y M. Adaptive filtering algorithm in GPS/DR integrated navigation[J]. Journal of Geomatics Science and Technology, 2008, 25(3): 206-208.

[9] WANG L, ZHAI C, JIN W, et al. Enhanced GPS measurements simulation for space-oriented navigation system design[J]. Chinese Journal of Aeronautics , 2010, 23(4): 438-446.

[10] 王立端. 星载GNSS/INS超紧组合技术研究[D]. 上海交通大学，2010. WANG L D. Research on ultra-tight GNSS/INS integration for autonomous spacecraft navigation[D]. Shanghai Jiao Tong University, 2010.

[11] 秦峰. 基于矢量跟踪的高动态载体超紧组合导航技术研究[D]. 上海交通大学2014. QIN F. Research on vector tracking based ultra-tightly integrated navigation for high dynamic vehicles[D]. Shanghai Jiao Tong University, 2014.

[12] CUI X, YANG Y. Adaptively robust filtering with classified adaptive factors[J]. Natural Science, 2006, 16(8): 841-846.

Adaptive Robust Filter for INS/CNS/GNSS IntegratedNavigation of the LEO Spacecraft

QIN Feng, SONG Zhenhua, WU Zhen

(ShanghaiElectro-MechanicalEngineeringInstitute,Shanghai, 201109,China)

The low earth orbit (LEO) spacecraft has high requirement for the stability of navigation system. If the standard Kalman filter is used to the integrated navigation system, large errors might occur and the navigation accuracy of the LEO spacecraft will decrease when abnormal disturbances occur. Hence, an adaptive robust filter is proposed to apply to the navigation system of LEO spacecraft, and then the INS/CNS/GNSS integrated navigation is designed based on it. To verify the effectiveness of the adaptive robust filter, simulation experiments are implemented respectively for the integrated navigations with the standard Kalman filter and adaptive robust filter.

integrated navigation； adaptive, robust； Kalman filter； LEO spacecraft

V249

A

1674-1579(2017)02-0055-05

10.3969/j.issn.1674-1579.2017.02.009

2017-01-22

秦 峰(1986—)，男，工程师，研究方向为惯性导航、天文导航、组合导航等；宋振华(1980—)，男，高级工程师，研究方向为惯性导航、组合导航、卫星导航等；吴 镇(1985—)，男，工程师，研究方向为惯性导航.