基于高斯伪谱法的空天飞机上升段最优轨迹设计*

张佩俊，刘鲁华，王建华

(国防科学技术大学航天科学与工程学院，长沙 410073)



基于高斯伪谱法的空天飞机上升段最优轨迹设计*

张佩俊，刘鲁华，王建华

(国防科学技术大学航天科学与工程学院，长沙 410073)

针对复杂多约束条件下空天飞机上升段燃料最优轨迹优化问题，提出一种基于高斯伪谱法的上升段轨迹优化策略.依据发动机的推力特性将上升轨迹合理分段，使原最优控制问题转化为多段最优控制问题后,采用高斯伪谱法进行并行优化计算.数值仿真结果表明采用这种轨迹优化策略能够满足组合动力系统工作模态转换时对飞行状态的约束条件，可以在较短的时间内完成高精度的上升段轨迹优化任务，从而验证了该方法的有效性.

空天飞机；燃料最优；分段优化；高斯伪谱法

0 引 言

研究满足廉价、快速与高可靠性等要求的新型天地往返运输系统已经成为新的研究热点，多个航空航天强国都已提出了发展空天飞机的研究计划. 如英国在1991年就提出了“SKYLON”空天飞机研究计划，目前该计划已在新型预冷式组合发动机的研制方面取得了重大突破并预计在2030年实现首飞[1-2]；此外，日本提出了将完全可重复使用的两级入轨组合动力飞行器作为未来天地往返运输平台这一空天战略，目前针对该飞行器的相关研究仍在持续进行[3]. 为了赶超世界先进水平，在2016年8月中国也提出了组合动力飞行器的研制计划，这种飞行器将集成涡轮、冲压和火箭发动机等多种动力模式，预计在2030年达到飞行试验的水平. 目前，组合动力系统的集成方式主要有串联式和并联式这两种方式[4]，所使用的推进剂主要有碳氢或者液氢液氧燃料，此外，分别以液氢、碳氢燃料为推进剂的超燃冲压发动机均得到了成功验证[5]，从而极大地降低了组合动力发动机的研制难度.由于空天飞机能够很好地克服传统运载模式的缺点，大幅度提高进入空间的安全性并降低空天往返的运输费用，因此具有极其广阔的发展前景. 最优轨迹设计是飞行器设计的核心技术之一，能降低对结构、材料和发动机等专业的设计要求，因此对空天飞机最优上升轨迹的研究具有重要的意义.

飞行器最优轨迹的设计方法主要包括直接法和间接法. 间接法具有计算精度高、计算结果具有一阶最优必要性条件等优点，不足之处在于推导过程较为复杂，猜测没有物理含义的协态变量的初始值较为困难；直接法主要有伪谱法、直接打靶法、遗传算法和模拟退火等方法，无需进行复杂而繁琐的最优控制一阶必要性条件的推导，在求解复杂约束条件下的最优轨迹时更有优势[6]. 文献[7]研究了空天飞机上升段最优轨迹设计问题，提出了分段优化的策略并将攻角与推力阀门进行离散化，利用配点法求解得到最优控制量. 文献[8]采用间接法设计了空天飞机上升段最优轨迹，利用数值打靶法求解转化后的两点边值问题. 由于在发动机工作模态转换时协态变量会出现突变，因此原最优控制问题将转化为多段两点边值问题，从而极大地增加了问题的求解难度. 文献[9]针对X-51飞行器空基投放后上升段轨迹优化问题提出了分段优化的思想，将上升轨迹分段后利用遗传算法和序列二次规划算法设计了最优燃料轨迹，但没有涉及飞行器水平起飞后爬升阶段的轨迹设计. 文献[10]利用混合粒子群算法设计了RLV飞行器的上升段轨迹，但计算量较大、计算耗时问题十分突出. 文献[11]采用共轭梯度法与动态规划法对两级入轨空天飞机的最优分离速度进行了研究. 文献[12]利用高斯伪谱法设计了两级入轨飞行器的最优上升轨迹，仿真结果表明高斯伪谱法具有计算精度与计算效率较高的优点.

已有的研究主要集中于垂直起飞式飞行器的上升段轨迹设计或两级入轨飞行器在级间分离后的轨迹设计，而对组合动力飞行器水平起飞后爬升段轨迹的研究不够充分. 组合动力飞行器的推力与飞行状态密切相关，在发动机工作模态切换时对飞行器飞行状态的约束较为严苛，从而给上升段轨迹优化设计带来了极大的困难. 近几年，高斯伪谱法因其计算精度高、速度快等优势获得了研究者的广泛关注，但该方法存在计算节点的选择较为困难，盲目增加计算节点数容易造成计算量大、计算耗时等问题. 因此，本文以一种新型水平起降式空天飞机为研究对象，依据组合动力系统工作模态的不同将上升段轨迹进行分段处理，合理分配在各个阶段的计算节点数，之后采用高斯伪谱法进行轨迹优化设计.

1 问题描述

空天飞机从跑道上水平起飞后进入爬升阶段，在该阶段组合动力系统依据飞行状态依次切换至涡轮、超燃冲压和火箭发动机工作模态. 为了保证冲压发动机能够正常工作，在其工作期间飞行速度应严格满足约束条件(如表1所示)且推力大小连续可调. 假设发动机工作模态的切换过程在瞬间完成，即不考虑两种发动机同时工作的情况，飞行器的飞行任务是为国际空间站进行货物补给，所采用的飞行时序如1.1节所示.

1.1 飞行时序

1)飞行器在爬升段首先启动涡轮发动机工作，当飞行速度达到M1、飞行高度达到h1时组合动力系统切换至超燃冲压发动机工作模态. 此后飞行器继续提速爬升飞行直至飞行速度达到M2、飞行高度达到h2，此时组合动力系统切换至火箭发动机工作模态. 其中M1、h1、M2和h2由优化算法得到.

2)在火箭发动机的推动下飞行器进入与目标轨道共面的椭圆轨道近地点，轨道的近地点高度为90 km，远地点高度为200 km.

3)当到达椭圆轨道远地点时飞行器点火加速以进入近地圆轨道(高度为200 km)，在近地圆轨道上等待一定时间后采用霍曼转移的方式实现与目标航天器交会对接.

图1为上升段轨迹在纵平面的投影示意图，图2 为飞行器在轨道转移过程的示意图.

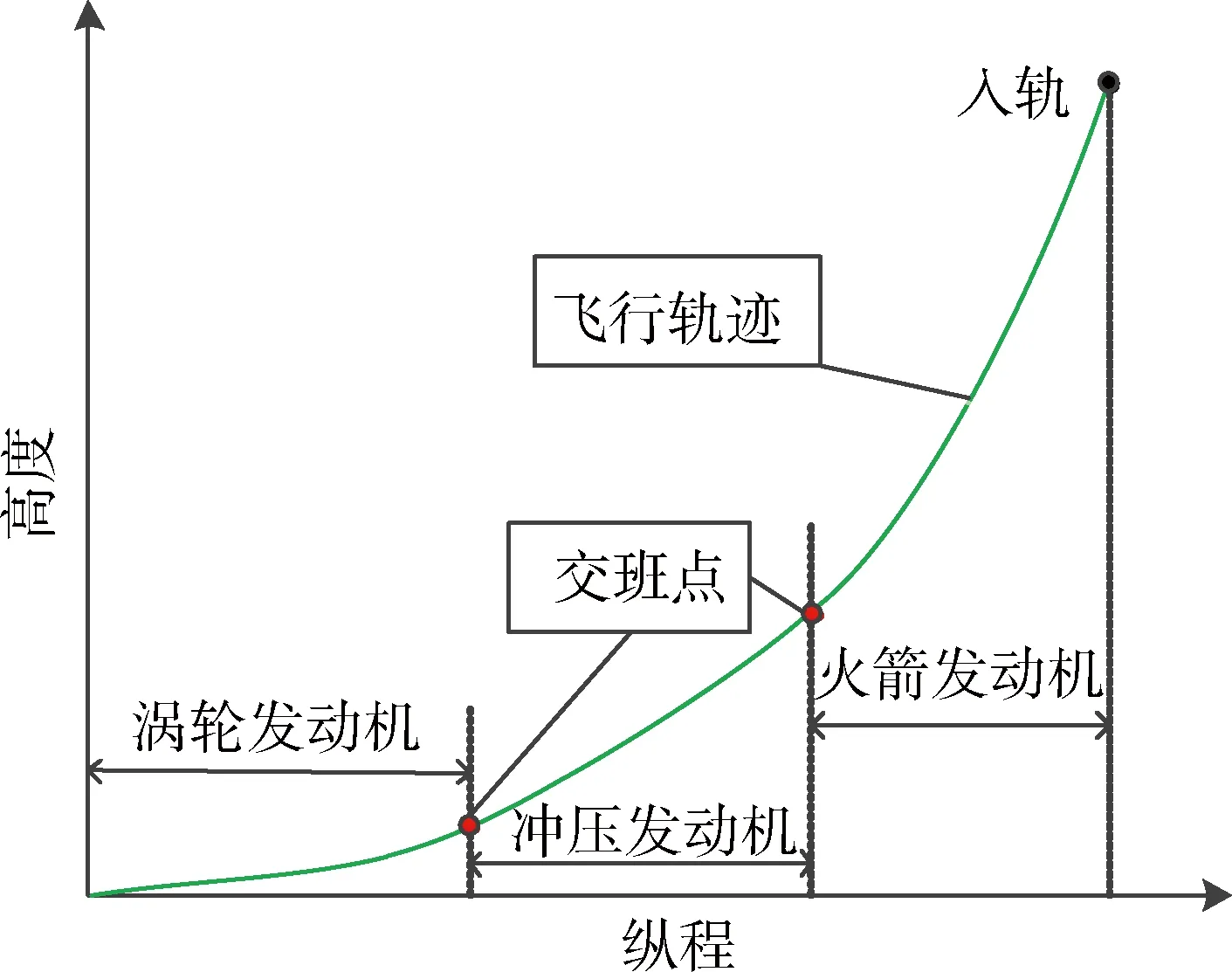
图1 上升段飞行剖面示意图Fig.1 Sketch map of ascent trajectory on the vertical plane

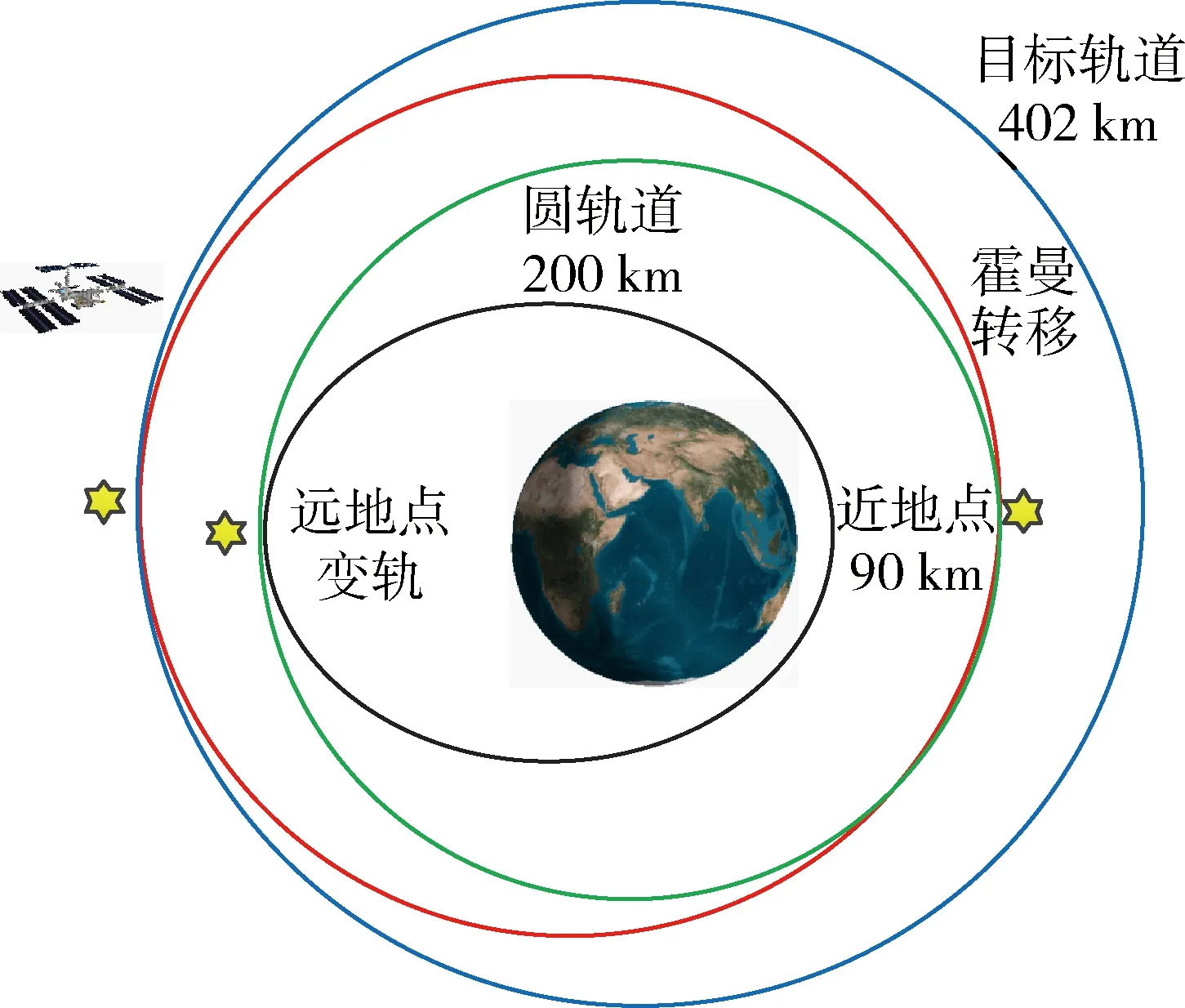
图2 轨道转移过程示意图Fig.2 Sketch map of orbital transfer sequence

1.2 性能指标

该新型空天飞机的发动机推力沿体轴方向，控制变量为攻角、倾侧角和推力阀门大小. 最优燃料问题可描述为：设计攻角、倾侧角与推力阀门大小，在满足过程约束与终端约束的条件下，在终端时刻飞行器的质量最大，因此性能指标可以表示为

minJ=-mf

(1)

式中mf为飞行器在终端时刻的质量.

1.3 动力学模型

在半速度坐标系下飞行器的动力学模型可简化为

(2)

式中，α—攻角，ν—倾侧角，V—飞行速度，CD—阻力系数，CL—升力系数，S—参考面积，r—地心距，θ—当地速度倾角，f—引力常数，m1—地球质量，m—飞行器质量，ρ—空气密度，σ—方位角，速度方向与正北方向之间的夹角，逆时针为正，φ—纬度，λ—经度，Isp—推进剂比冲，g—当地重力加速度，T—组合发动机的推力.

1.4 无纲量化方法

由于飞行器的运动状态参数在量级上存在很大的差异，对优化计算十分不利，因此在优化计算前先进行无量纲化处理. 对地心距r、速度大小V和时间t作如下处理：

(3)

(4)

1.5 约束条件

(1)起始状态约束

x0=[V0θ0σ0φ0λ0r0m0]

(2)过程约束

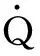
(5)

式中Kh为热流密度系数. 考虑到飞行器控制能力有限，控制量大小与变化率都受到一定的限制

(6)

(3)终端状态约束

由于在上升段结束后飞行器进入与目标轨道共面的椭圆轨道的近地点，因此其终端状态需满足如下等式约束条件:

(7)

式中，Ω为目标轨道的升交点赤经，i为轨道倾角，ωe为地球自转角速度，td为飞行器的等待时间，tf为上升段飞行时间，下标f代表各状态量的终端值. 式(7)中第一个等式用于求解终端的速度方位角，第二个等式用于求解最优起飞时间.

由此可知，飞行器在飞行过程中受到的过程约束和终端约束较为复杂，设计出满足复杂多约束条件的最优轨迹具有很大的难度.

2 轨迹分段策略

由于空天飞机一般采用组合动力系统，而组合动力系统的可用推力与飞行状态高度耦合，在不同的飞行阶段，飞行环境、最大可用推力与推进剂比冲的变化十分剧烈，给轨迹优化设计带来了极大的困难. 因此，通过将上升段轨迹合理分段后进行优化，在状态参数变化较为剧烈的阶段采用较多的计算节点数，在状态参数变化较为光滑的阶段可适当减少计算节点数，从而实现在不降低计算精度的前提下快速生成满足多约束条件的最优轨迹.

传统的轨迹分段方法主要有依据飞行时间、航路点、飞行状态等[13]，对于空天飞机而言，在发动机工作模态切换时对飞行器的飞行状态有着十分严苛的约束，因此可将发动机工作模态的切换点作为分段点(如图3所示)，从而较为方便地考虑发动机工作模态切换时飞行状态所受的约束. 研究中将上升段轨迹分为3段：涡轮发动机、超燃冲压发动机和火箭发动机工作阶段. 在涡轮发动机和超燃冲压发动机工作时飞行器的飞行高度较低，气动特性和推力特性变化十分剧烈，因此需要相应地增加计算节点数；在火箭发动机工作阶段，虽然可获得的推力较大，但此时飞行器的飞行高度较高，气动特性的变化对飞行状态的影响较小，推力特性与飞行状态无关，因此可适当减少计算节点数. 增加每段起始与终端位置处分布的节点，从而保证分段点的飞行状态满足约束条件，使飞行器顺利地实现发动机工作模态的转换. 研究中首先根据上升段动力学特性设计出控制量剖面，之后进行数值积分得到各段弹道优化时的初值，轨迹优化流程如图4所示.

图3 轨迹分段方法Fig.3 Segmentation method

图4 轨迹优化流程框图Fig.4 Block diagram of the optimization procedure

3 轨迹优化原理

高斯伪谱法是直接法的一种，同时离散控制量与状态量并在离散节点上采用拉格朗日插值多项式来近似控制变量与状态变量，从而将连续空间的最优控制问题转化为非线性规划问题，之后利用非线性规划方法进行求解.

设上升段第i(i=1,2,3)段的飞行时间区间为[t0,tf]，为优化问题的方便一般需将时间区间转化到区间内，对时间变量作如下变换：

(8)

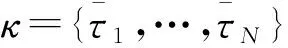
(9)

(10)

(11)

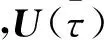
(12)

至此可将动力学微分方程约束转换为代数方程约束

(13)

性能指标、终端约束与过程约束经过高斯伪谱法离散后，就可以将多约束条件下的最优控制问题转化为离散形式的非线性规划问题，之后采用序列二次规划算法(SQP)进行求解. 由于上升轨迹共分为3段，因此上述离散过程执行3次.

4 仿真分析

以某单级入轨空天飞机为研究对象[14]，设计该飞行器的燃料最优上升轨迹. 飞行器起飞时总质量为136 605 kg，在跑道上以160 m/s的速度水平起飞，组合发动机的推力表达式如式(14)～(16)所示，工作范围如表1所示.

(1)涡轮喷气发动机推力的表达式为：

T=4.448τ(2.99×105-10h+1.331 0-4h2-6.481 0-10h3+3 750M3)

(14)

(2)超燃冲压发动机推力的表达式为：

T=4.448τ(1 033M2-13 530M+152 400)

(15)

(3)火箭发动机推力的表达式为：

T=4.448(-16 400+669 295τ)

(16)

其中τ为推力阀门，h为飞行高度，M为马赫数.

表1 发动机的工作范围Tab.1 Engine types and constraints

仿真中考虑的约束条件主要有：

(1)起始条件：

x0=[160 m/s,0,0,0,0,637 813 7 m,136 605 kg]

(2)过程约束：

(3)终端约束：

θf=0,hf=90 km，vf=7 883 m/s，终端速度方位角σf与经度λf满足式(7).

表2和表3给出了高斯伪谱法与数值积分结果的精度对比情况，由此可以看出飞行器的终端状态量具有很高的计算精度，相对误差一般小于 2.38%.上升段飞行时间为765.80 s，图5～8给出了高斯伪谱法的计算结果与数值积分结果的对比情况.

表2 伪谱法与数值积分的结果对比Tab.2 Comparison of the results obtained from GPM and numerical integration

表3 轨道要素结果对比Tab.3 Comparison of the orbital elements

设置模式搜索算法的相对步长和步长缩减因子为0.5，粒子群算法的粒子个数为130，全局增量为0.8，最大速度为0.06，表4给出了在内存为4 GB、主频为2.8 GHz的普通微机上，基于Matlab®2015a平台利用高斯伪谱法、模式搜索和粒子群算法进行优化计算的计算耗时与终端状态量的计算精度对比结果. 从对比结果可以看出，利用高斯伪谱法进行轨迹优化计算的耗时在4 min左右，远少于其余两种优化方法. 虽然模式搜索算法的计算精度与高斯伪谱法相近，但前者的计算耗时十分明显，性能指标也较差. 粒子群算法得到的终端状态量的计算精度较低，计算耗时通常在2 h左右. 由此可知高斯伪谱法具有计算精度高和收敛速度快的特点，能够满足快速设计空天飞机上升段最优轨迹的要求.

图5 速度随时间变化曲线Fig.5 Time history of the velocity

图6 高度随时间变化曲线Fig.6 Time history of the altitude

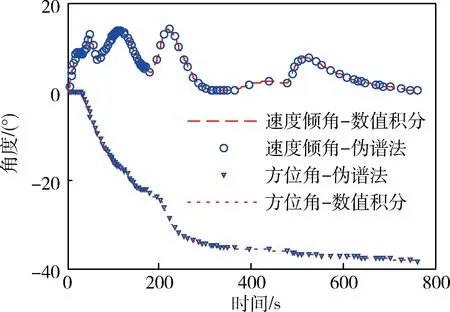
图7 速度倾角和方位角随时间变化曲线Fig.7 Time history of the flight path angle and heading angle

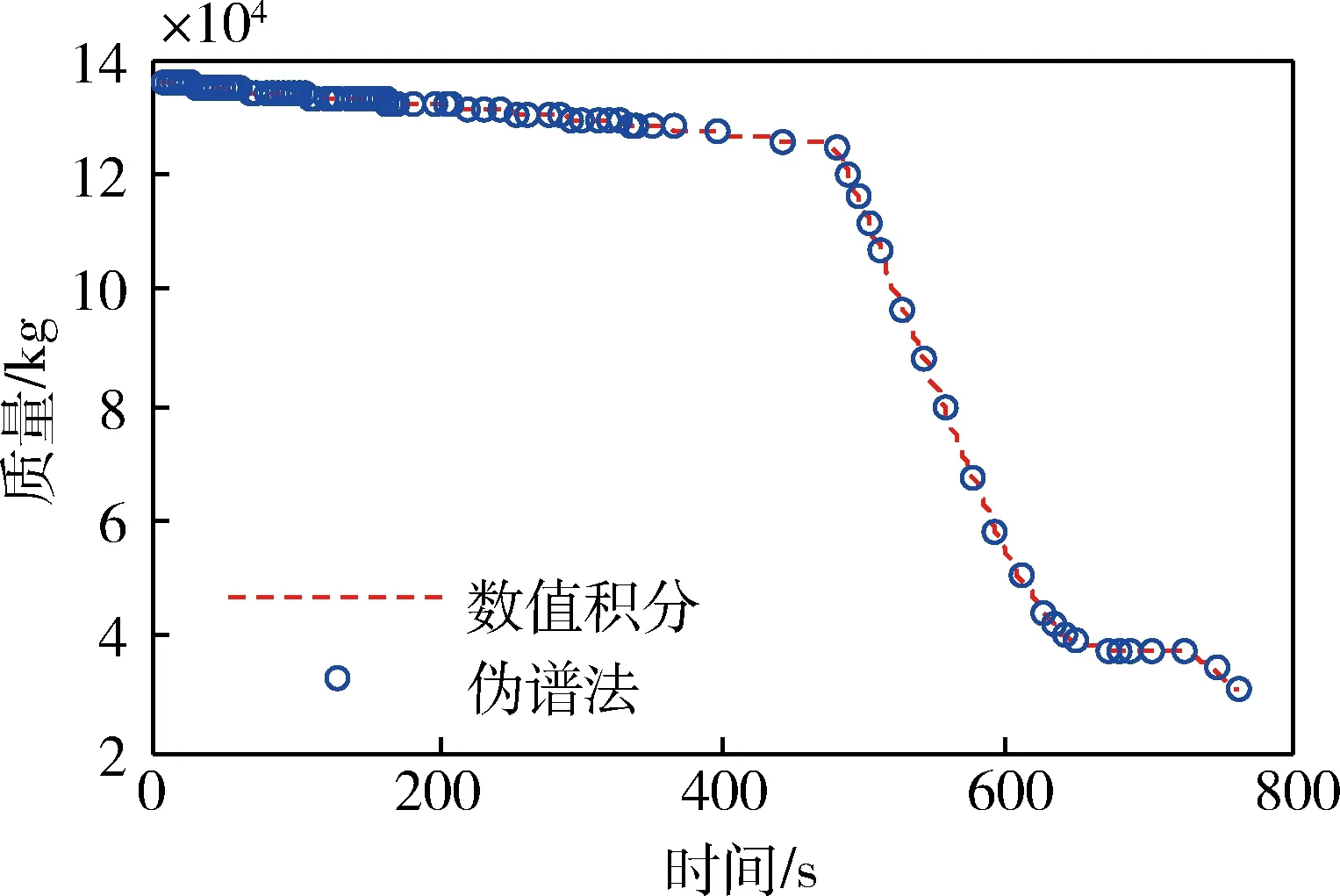
图8 质量随时间变化曲线Fig.8 Time history of the mass

表4 伪谱法与其它优化算法的计算精度对比
Tab.4 Comparison of the results obtained from GPM and other optimization methods

终端状态量标准值伪谱法(积分值)模式搜索算法粒子群算法速度/(m/s)7883.007882.007883.047769.56高度/km90.0090.4090.0189.45速度倾角/(°)0.000.200.310.14质量/kg无30748.0130386.2030750.21计算耗时/s无245.003789.007354.00

由于高斯节点具有在端点位置分布密集、中间位置分布稀疏的特点，因此对于具有震荡特点的状态量会存在计算精度相对较低的情况. 仿真中发现速度倾角会出现一定的振荡现象，因此高斯伪谱法与数值积分的结果会存在较小的差异. 飞行过程中的倾侧角较小(如图9所示)，这与飞行器的升阻比、气动升力较大有关，飞行器能够通过较小的倾侧角即可完成较大幅度的转弯飞行. 在飞行器进行跨音速飞行时阻力系数大幅度增加，为了突破音障飞行器需要减小攻角，因此在前200 s内攻角出现较大幅度的下降现象(如图9所示).在吸气式发动机工作阶段，飞行器能够有效地利用燃料以提高飞行速度与高度，因此推力阀门始终保持在最大值(如图10所示).

在飞行速度接近Ma=5时飞行器切换至火箭发动机工作模态而不是一直工作至超燃冲压发动机所允许的最大飞行速度后才切换至火箭发动机，因为当飞行器的飞行速度超过这一速度时，超燃冲压发动机的工作效率反而会降低，这与文献[15]得到的结论一致. 随着飞行高度与速度的增加，超燃冲压发动机所能提供的推力与气动升力不断降低，因此在该阶段攻角始终为最大值. 飞行器飞行高度较低时动压快速增加并达到峰值，当飞行速度较大时最大热流密度达到峰值(如图11所示). 飞行过程中的过载、动压与最大热流密度均未超过最大限制，控制量攻角、倾侧角和推力阀门大小的变化较为平滑，对控制系统较为有利.

图9 倾侧角和攻角随时间变化曲线Fig.9 Time history of the bank angle and the angle of attack

图10 推力阀门随时间变化曲线Fig.10 Time history of the thrust throttle

图11 动压和最大热流密度随时间变化Fig.11 Time history of the dynamic pressure and heat rate

对于天地往返运输器而言，发射窗口的设计是一个很重要的研究内容. 传统运载器的发射窗口比较狭窄，因此必须进行精确的设计，而以组合动力发动机为推进系统的空天飞机可以在大气层内长时间飞行，跨越较大的地理空间后进入目标轨道，因此发射窗口一般较宽.从图12可以看出，当发射时间较最优发射时间提前近2 000 s时，完成轨道交会后飞行器的剩余质量仅减少了360 kg，因此组合动力飞行器的发射时间将更加灵活.

图12 交会后剩余质量随发射时间提前量的变化Fig.12 Mass after rendezvous with respect to take-off timing

5 结 论

本文以某水平起降式空天飞机为研究对象，利用高斯伪谱法设计了飞行器在复杂多约束条件下的燃料最优轨迹并对发射窗口进行了讨论. 为了解决高斯伪谱法在计算节点选择上的困难，提出依据发动机的工作模态对飞行轨迹分段后进行并行优化的策略，并得到如下结论：1)吸气式发动机的燃油效率高，能有效地提高飞行高度与速度，因此在该阶段飞行时发动机推力始终保持在最大值；2)在飞行速度较低时动压较大，在飞行速度较高时最大热流密度约束占主导地位；3)组合动力飞行器的发射窗口较宽，具有较好的任务适应性.

由于在研究中仅考虑了以燃料最优作为性能指标的上升段轨迹设计问题，而在实际应用中通常还需兼顾其它多种因素，比如上升段飞行时间、轨迹跳跃幅度等，因此未来需开展针对空天飞机上升段多性能指标的轨迹优化方法研究.

[1] MARK H, ROGER L. SKYLON user’s manual[M]. Reaction Engines Limited, 2014-01.

[2] 康开华. 英国“云霄塔”空天飞机的最新进展[J]. 国际太空, 2014(7): 42-50. KANG K H. The latest research progress of SKYLON in British[J]. International Aerospace, 2014(7): 42-50.

[3] FUJII K, ISHIMOTO S, MUGITANI T, et al. Present status and prospects of JAXA’s research on future space transportation system[C]//The 18thAIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference. Washington D.C.:AIAA, 2012.

[4] 彭小波. 组合循环动力技术在天地往返领域的发展与应用[J]. 导弹与航天运载技术, 2013(1):78-82. PENG X B. Development of combined cycle propulsion technology in reusable launch vehicle [J]. Missile and Space Vehicles, 2013(1):78-82.

[5] 黄伟. 临近空间高超声速飞行器内外流一体化设计及飞行性能研究[D]. 长沙：国防科学技术大学，2010. HUANG W. Combined analysis on internal/external flows of hypersonic vehicles in the near-space and CFD predictions of its flying performance[D]. Changsha:National University of Defense Technology, 2010.

[6] 黄国强, 陆宇平, 南英. 飞行器轨迹优化数值算法综述[J]. 中国科学, 2012(9): 006. HUANG G Q, LU Y P, NAN Y. A survey of numerical algorithms for trajectory optimization of flight vehicles [J]. Science China, 2012(9): 006.

[7] NGUYEN H N. Optimal ascent trajectories of the horizontal takeoff single-stage and two-stage-to-orbit launchers[C]//AIAA Guidance, Navigation and Control Conference. Washington D.C.:AIAA, 1991.

[8] CHUDEJ K, BULIRSCH R. Numerical solution of a simultaneous staging and trajectory optimization problem of a hypersonic space vehicle[C]//AIAA and DGLR, International Aerospace Planes and Hypersonic Technologies Conference. Washington D.C.:AIAA, 1993.

[9] 张侃. 基于多任务多目标的空天飞行器轨迹设计及优化研究[D]. 南京：南京航空航天大学，2010. ZHANG K. Research on spacecraft trajectory design and optimization based on multi-task and multi-target [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010.

[10] 张鼎逆，刘毅. 基于混合粒子群法的RLV 上升段轨迹优化[J]. 江苏大学学报：自然科学版，2013,34(1)：54-59. ZHANG D N, LIU Y. Optimization of RLV rising trajectory based on hybrid particle swarm optimization[J]. Jiangsu University: Natural Science Edition, 2013, 34 (1): 54-59.

[11] 黄国强，南英，陆宇平. 二级入轨空天飞行器上升轨迹优化[J]. 宇航学报, 2010,31(3):641-647. HUANG G Q, NAN Y, LU Y P. Optimization of ascending trajectory of a two-stage-to-orbit space planes [J]. Journal of Astronautics space,2010,31(3): 641-647.

[12] FUJIKAWA T, TSUCHIYA T, TOMIOKA S. Multi-objective, multidisciplinary design optimization of TSTO space planes with RBCC Engines[C]//The 56thAIAA/ASCE/AHS/ASC Sctructures, Structural Dynamics, and Meterials Conference. Washington D.C.: AIAA, 2015.

[13] 谢愈, 刘鲁华, 汤国建, 等. 多约束条件下高超声速滑翔飞行器轨迹优化[J]. 宇航学报, 2011, 32(12): 2499-2504. XIE Y, LIU L H, TANG G J, et al. Optimization of hypersonic glide spacecraft under multiple constraints[J]. Journal of Astronautics, 2011, 32 (12): 2499-2504.

[14] SHAUGHNESSY J D, PINCKNEY S Z, MCMINN J D, et al. Hypersonic vehicle simulation model: winged-cone configuration[R]. NASA 19910003392, 1990.

[15] TSUCHIYA T, MORI T. Optimal design of Two-Stage-to-Orbit space planes with airbreathing engines[J]. Journal of Spacecraft and Rockets, 2005, 42(1):90-97.

Optimal Ascent Trajectory Design for Single-Stage-to-Orbit Space PlanesBased on Gauss Pseudospectral Method

ZHANG Peijun, LIU Luhua, WANG Jianhua

(CollegeofAerospaceandScienceEngineering,NationalUniversityofDefenseTechnology,Changsha410073，China)

To design the fuel optimal ascent trajectory of space planes under complex and multi-constrained conditions, a strategy is proposed to segment the ascent trajectory according to the thrust characteristics of the engines. When the original optimal control problem is transformed into a multi-stage optimal control problem, the Gauss pseudospectral method is used for parallel optimization. Numerical result shows that this strategy can easily satisfy the constraints of state variables when the engine switches and generates the fuel optimal trajectory within short computing time. It is verified that the optimization strategy proposed is efficient.

space planes； fuel optimal； multiple-stage optimization； Gauss pseudospectral method

资助项目(11502289). 收稿日期：2016-11-28

V412

A

1674-1579(2017)02-0011-08

10.3969/j.issn.1674-1579.2017.02.003

张佩俊(1990—)，男，硕士研究生，研究方向为飞行器轨迹优化、制导与控制;刘鲁华(1977—)，男，副教授，研究方向为飞行器动力学、制导与控制;王建华(1988—)，男，博士研究生，研究方向为制导与控制及一体化设计.