基于干扰观测器的挠性卫星姿态滑模变结构控制*

王雪冰，吴 忠

(北京航空航天大学仪器科学与光电工程学院，北京 100191)



基于干扰观测器的挠性卫星姿态滑模变结构控制*

王雪冰，吴 忠

(北京航空航天大学仪器科学与光电工程学院，北京 100191)

为抑制各种内外干扰因素对挠性卫星姿态控制性能的影响，设计基于干扰观测器的滑模变结构控制器.该控制器采用干扰观测器对系统中存在的内外干扰进行估计，并对估计值加以前馈补偿.在此基础上，采用滑模变结构控制器对未补偿的干扰进一步抑制，实现卫星姿态与姿态角速度的渐近收敛.与单纯的滑模变结构控制器相比，本文的控制器已根据干扰估计值对干扰进行了前馈补偿，采用较小的切换增益即可抑制剩余干扰，颤振现象减弱.仿真结果表明，本文设计的控制器是可行的.

挠性航天器；姿态控制；干扰观测器；滑模变结构控制

0 引 言

为满足未来航天任务的复杂需求，挠性卫星的姿态必须具有足够高的精度和稳定度[1].然而，在挠性卫星姿态控制系统中，存在多种内外干扰，如太阳帆板挠性振动、太阳帆板驱动机构(SADA)干扰和环境干扰等，严重影响了其控制性能.因此，抗干扰姿态控制器设计一直是高精度高稳定度卫星所要解决的核心关键问题之一.

针对挠性卫星姿态控制问题，文献[2]设计了一种H∞鲁棒控制器，并以ETS-VI卫星为对象，进行了验证，但其控制器阶数偏高，且性能保守.文献[3]设计了基于姿态误差四元数的自适应姿态跟踪控制律，保证了卫星的姿态跟踪性能，但该方法处理快变参数和未建模动态的能力较弱.文献[4]针对挠性附件不确定干扰，设计了内模控制器，提高了控制精度，但是只考虑了正弦周期性干扰.文献[5]提出了一种双闭环自抗扰姿态控制器，具有较强的鲁棒性和干扰抑制能力，但其调试参数较多.滑模变结构控制具有设计方法简单、响应速度快、鲁棒性强的特点，如文献[6-9]均研究了挠性航天器的滑模变结构控制方案，但颤振现象是其固有缺陷.作为有效的干扰抑制策略，干扰观测器可以估计干扰并通过控制器进行反馈补偿，文献[10]设计了一种基于干扰观测器的前馈补偿控制系统，姿态精度达到了要求，但存在一定静差.

本文综合滑模变结构控制和干扰观测器的优点，提出了一种基于干扰观测器的滑模变结构控制器，通过干扰观测器有效估计干扰并进行前馈补偿，滑模变结构控制器对未补偿的干扰进一步抑制，既提高了姿态控制性能，又能有效减弱颤振现象.

1 动力学模型及问题描述

1.1 卫星姿态动力学模型

参照文献[11-12]，考虑带有单翼旋转挠性太阳帆板的受扰卫星，其动力学方程可表示为

(1)

式中，J为挠性卫星系统转动惯量，ω为卫星本体相对惯性系的角速度在本体系中的投影，Rs,sa为帆板驱动与星体驱动的耦合系数阵，l=[0 1 0]T为太阳帆板的驱动轴方向，ωsa为帆板转动角速度，Fs,sa为帆板振动与星体转动的耦合系数阵，u为卫星的控制力矩，η(t)=[η1(t)η2(t) …ηN(t)]T为太阳帆板的模态坐标矢量，N为模态阶数，ud为卫星受到的环境干扰力矩矢量，Isa为帆板关于铰链点的转动惯量，Fsa为帆板转动与帆板振动的耦合系数阵，Tsa为帆板的驱动力矩，Td为太阳帆板驱动机构的扰动力矩，x×表示x的3个分量构成的斜对称矩阵，矩阵C和K分别为阻尼和刚度矩阵，具体形式为

(2)

其中，ξ1,ξ2,…,ξN为阻尼比，Λ1,Λ2,…,ΛN为模态频率.

如设ωb为卫星本体系相对于轨道系的角速度，那么ω与ωb之间的关系可以表示为

ω=ωb+ωo

(3)

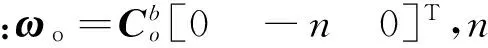
(4)

1.2 干扰力矩分析

在式(1)表示的动力学模型中，卫星不仅受到环境干扰力矩ud的影响，还受到SADA运动带来干扰的影响，下面将逐一分析.

(1)环境干扰力矩

卫星受到的空间环境干扰力矩主要包括：气动力矩up、重力梯度力矩ug、地磁力矩um和太阳光压力矩us[13].那么卫星受到总的环境干扰力矩可表示为：

ud=up+ug+um+us

(5)

需要说明的是，环境干扰力矩对卫星姿态的影响与其运动的轨道高度、结构分布情况和空间环境条件等有关.

(2)SADA干扰力矩

设SADA采用步进电机驱动，其谐波力矩及导电环的摩擦力矩是其干扰力矩的主要因素[14-17].

电机谐波力矩模型可以表示为[17]：

Tcog=Tksin(4Ntθsa)

(6)

其中，Tk为四阶齿槽力矩幅值，Nt为步进电机转子齿数，θsa为太阳帆板的转角.

导电环的摩擦力矩模型可以表示为[18]：

Tf=σ2ωsa+TCsign(ωsa)+

(TS-TC)e-(ωsa/ωS)2sign(ωsa)

(7)

其中，σ2是粘性摩擦阻尼系数，TC为库伦摩擦力矩，TS为最大静摩擦力矩，ωS为Stribeck转速.这样，SADA干扰力矩可表示为：

Td=Tcog+Tf

(8)

(3)转动惯量不确定性

帆板转动将引起整星转动惯量变化，设J0为卫星转动惯量中的确定部分，ΔJ为变化部分，那么整星转动惯量可表示为：

J=J0+ΔJ

(9)

将其代入式(1)中的第一式，可得：

(10)

1.3 问题描述

将式(3)代入式(10)，可得

(11)

定义等价干扰d为：

(12)

则式(11)可重写为

(13)

由此可见，如果把环境干扰、帆板驱动机构干扰、挠性附件振动等干扰因素统一视为等价干扰d，式(1)的动力学模型可以降阶为式(13)的形式.同时，对于由式(4)、式(13)描述的卫星系统，作如下假设：

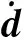
(14)

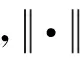
假设2.角速度ω和四元数[q0q]T均可直接测量或间接计算得到.

那么，挠性卫星姿态控制问题可以描述为，针对满足假设1、假设2的卫星系统式(4)、式(13)，考虑系统中存在的干扰，设计控制力矩u，使得

(15)

2 基于干扰观测器的滑模变结构控制器设计

2.1 干扰观测器设计

为抑制干扰d对姿态控制性能的影响，可对其进行前馈补偿.为此，需要获得干扰d的估计信息.根据文献[19-20]，设计干扰观测器如下：

(16)

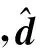
(17)

将式(17)代入式(16)的第二式，并整理可得

(18)

根据式(13)，式(18)可重写为

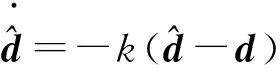
(19)

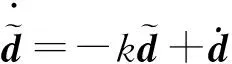
(20)

对式(19)求解，可得：

(21)

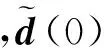
(22)

根据假设1及式(22)，可得：

(23)

可见，在式(16)的干扰观测器下，干扰估计误差是有界的.

2.2 控制器设计

在干扰观测器(16)的基础上，可以对滑模变结构控制器进行设计.定义滑动模态为

s=ωb+cq

(24)

其中，c>0为常数.

选取Lyapunov函数为

(25)

对式(25)两端求导，并将式(24)、式(13)和式(4)依次代入，整理可得

(26)

设计控制器u为

(27)

其中，k1、k2为大于0的常数，且

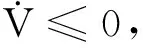
在式(27)的控制器下，式(26)可变为

(28)

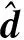
(29)

此时，Lyapunov函数的一阶导数式(26)将变为

(30)

3 仿真分析

为验证本文所设计控制器的有效性，本部分以某带有单翼旋转挠性太阳帆板的卫星为例，进行了仿真，并对滑模变结构控制器和基于干扰观测器的滑模变结构控制器的性能进行了对比.在仿真中，采用的卫星参数如下[21]：

根据以上参数，可计算得到：

考虑帆板的前五阶模态，其模态频率为：[Λ1,Λ2,Λ3,Λ4,Λ5]=[1.084 6,4.351 4,6.739 6,11.514 2,15.756 7]rad/s，阻尼比为：[ξ1,ξ2,ξ3,ξ4,ξ5]= [0.004,0.005,0.006 4,0.008,0.008 5]，初始模态坐标设为0.

设与SADA相关的干扰力矩参数为：Tk=0.06N·m，Nt=300，σ2=46N·m·s/rad，TC=0.01N·m，TS=0.02N·m，ωS=0.03(°)/s.设环境干扰力矩为：ud=10-3×[7.8cos(nt),1.6sin(nt)-2.6cos(nt),-1.2sin(nt)]TN·m，n=0.060(°)/s.

设卫星三轴姿态的初值为[1°,1°,-1°]，角速度初值为0(°)/s，并采用表1中的控制器参数，对卫星姿态控制系统进行了仿真，仿真结果如图1～图11所示.其中，SMC表示滑模变结构控制器，DO+SMC表示基于干扰观测器的滑模变结构控制器.

图1～3为卫星三轴姿态角变化曲线，可看出，进入稳态后，与SMC相比，基于干扰观测器的滑模变结构控制器使卫星姿态控制精度和稳定度明显提高，三轴姿态误差均小于2.1×10-6(°)，而SMC最大为3.4×10-5(°).图4～6为卫星三轴角速度曲线，可以看出，DO+SMC的角速度误差小于4.8×10-6(°)/s，而SMC角速度误差最大为6.5×10-5(°)/s.

表1 控制器参数Tab.1 Parameters of the controller

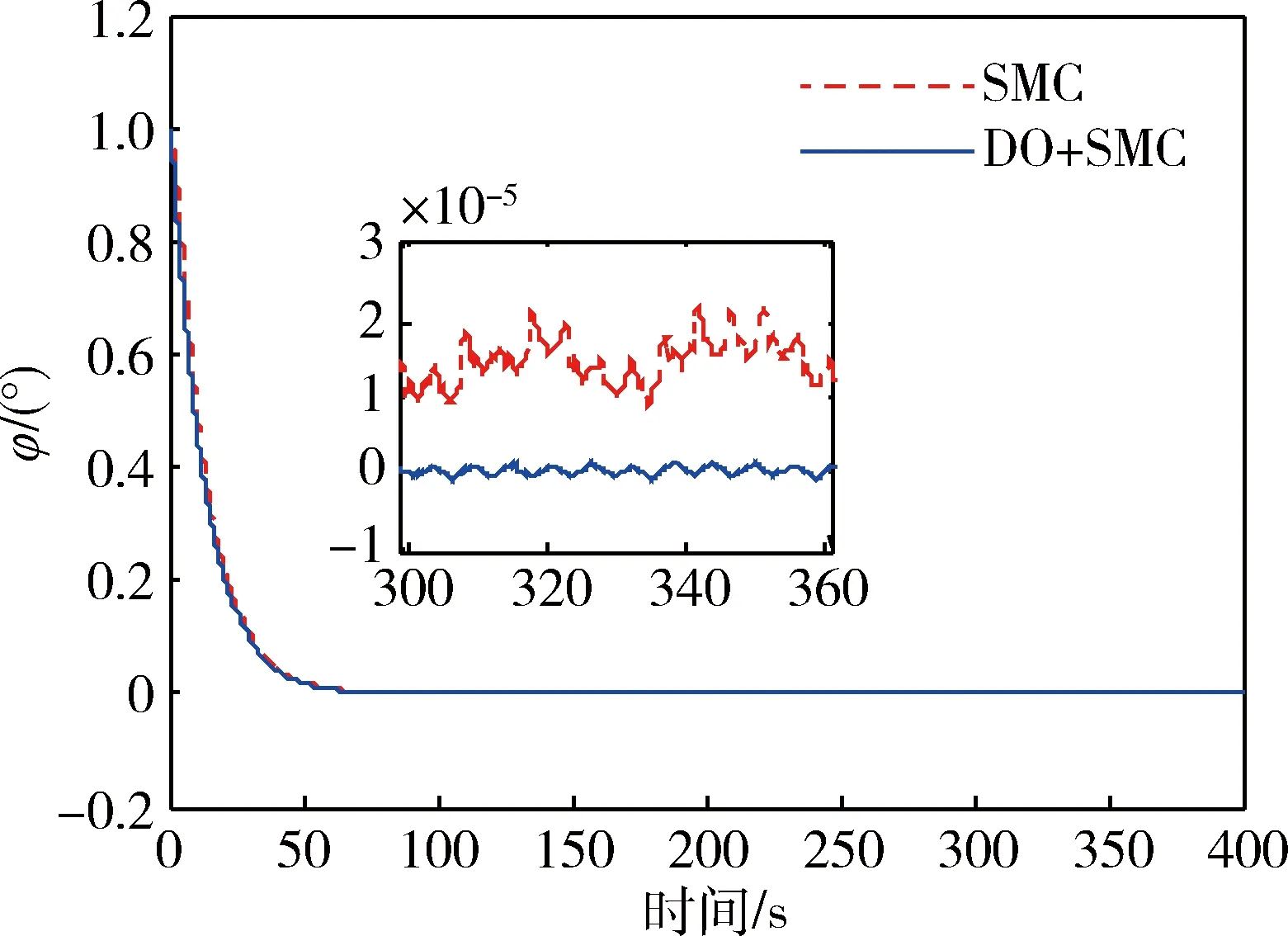
图1 滚转角变化曲线Fig.1 Time responses of roll angle

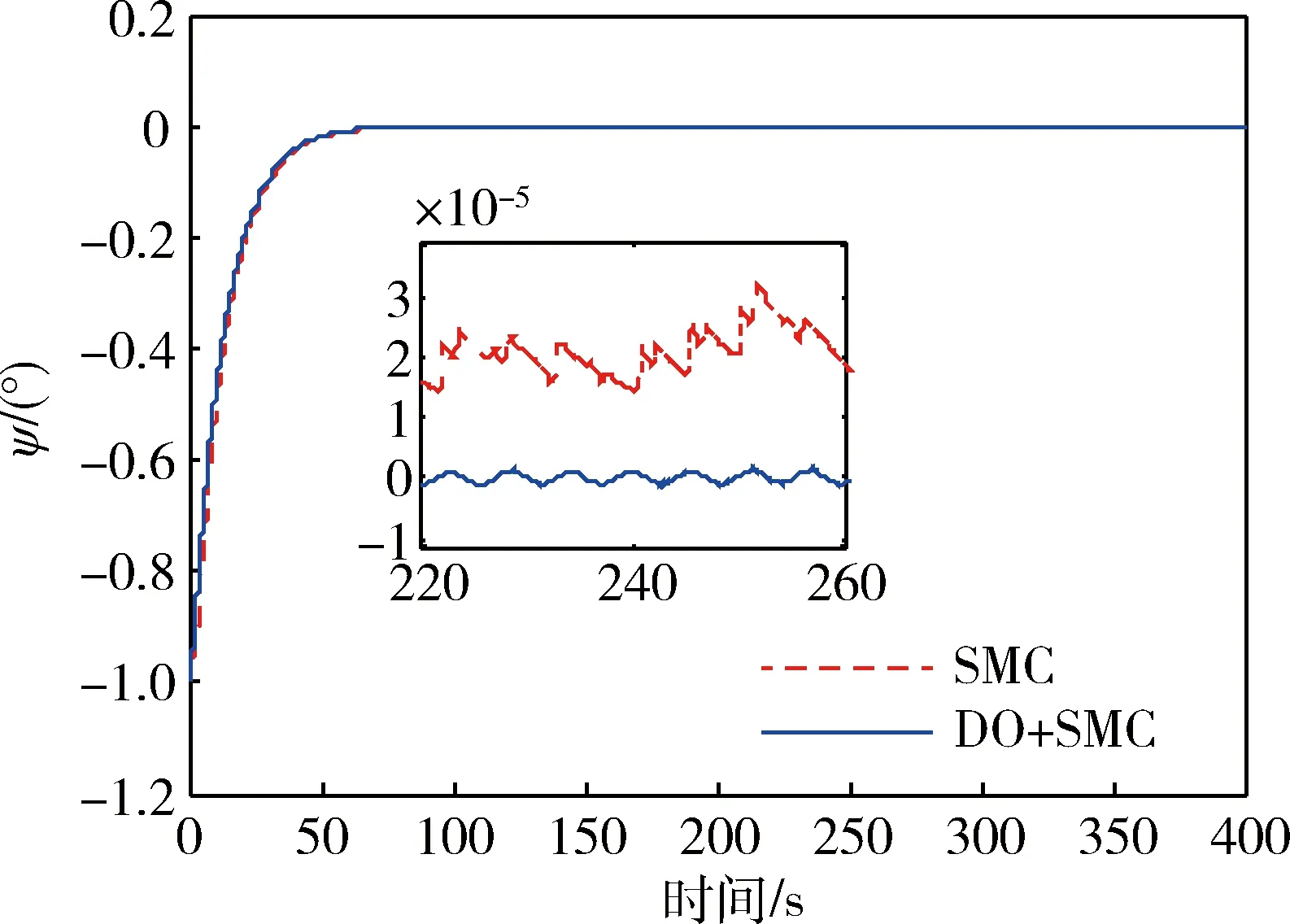
图3 偏航角变化曲线Fig.3 Time responses of yaw angle

图4 滚转角速度变化曲线Fig.4 Time responses of roll angular velocity

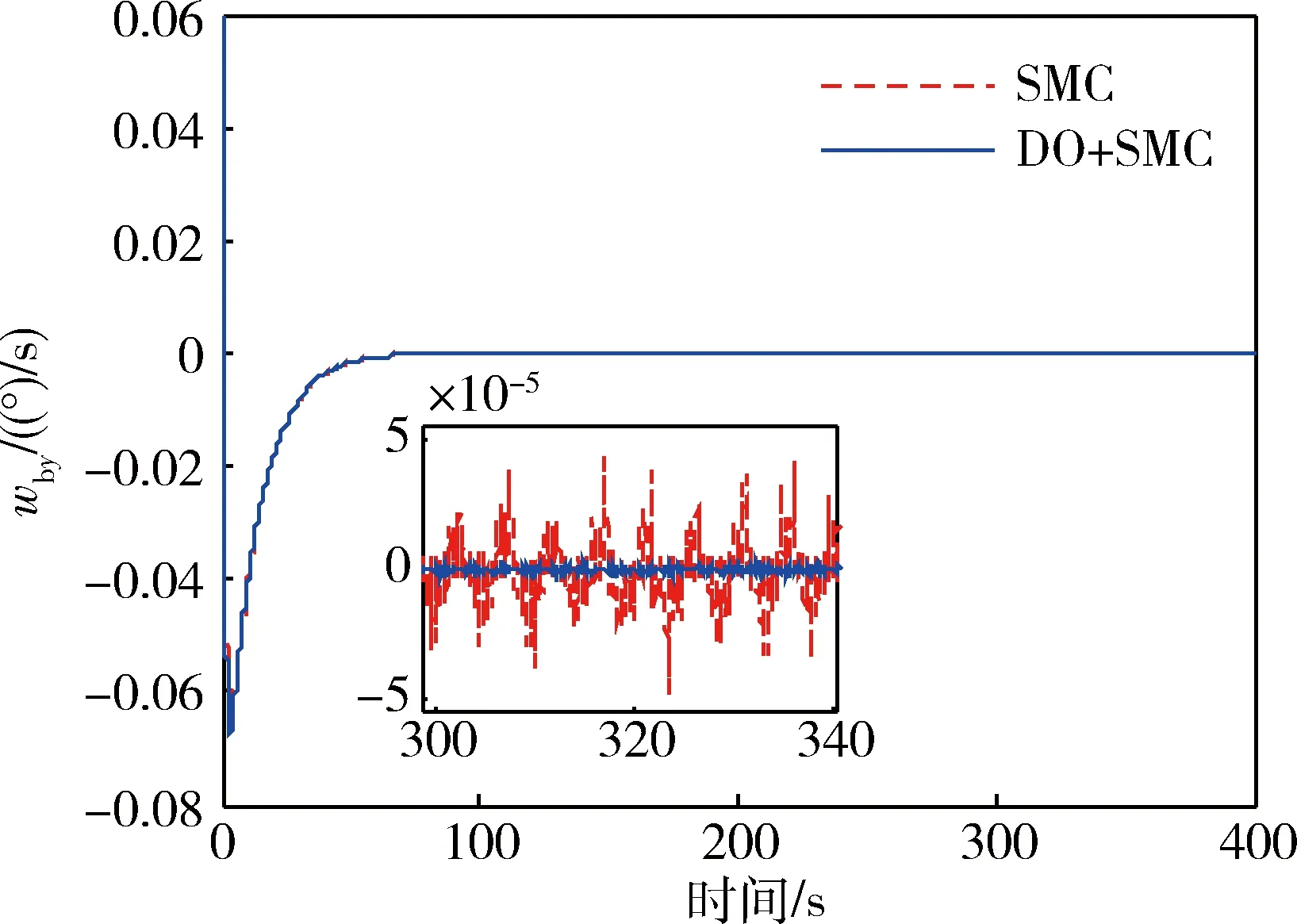
图5 俯仰角速度变化曲线Fig.5 Time responses of pitch angular velocity

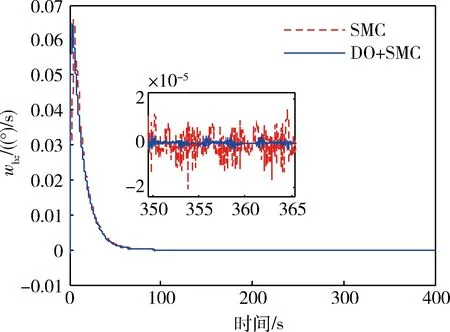
图6 偏航角速度变化曲线Fig.6 Time responses of yaw angular velocity

图7 DO+SMC滑模面变化曲线Fig.7 Time responses of sliding mode surface by DO+SMC

图7～8表示滑模面变化，对比看出，DO+SMC滑模面收敛速度更快、精度更高，颤振明显减弱.

图9～11分别为卫星三轴干扰力矩、干扰力矩估计和估计误差曲线.可以看出，所设计的干扰观测器能对环境干扰、帆板驱动机构干扰、挠性附件振动等干扰因素进行有效估计.其中滚转轴干扰估计误差小于实际值的2.8%，俯仰轴干扰估计误差小于实际值的2.6%，偏航轴干扰估计误差小于实际值的1.5%.

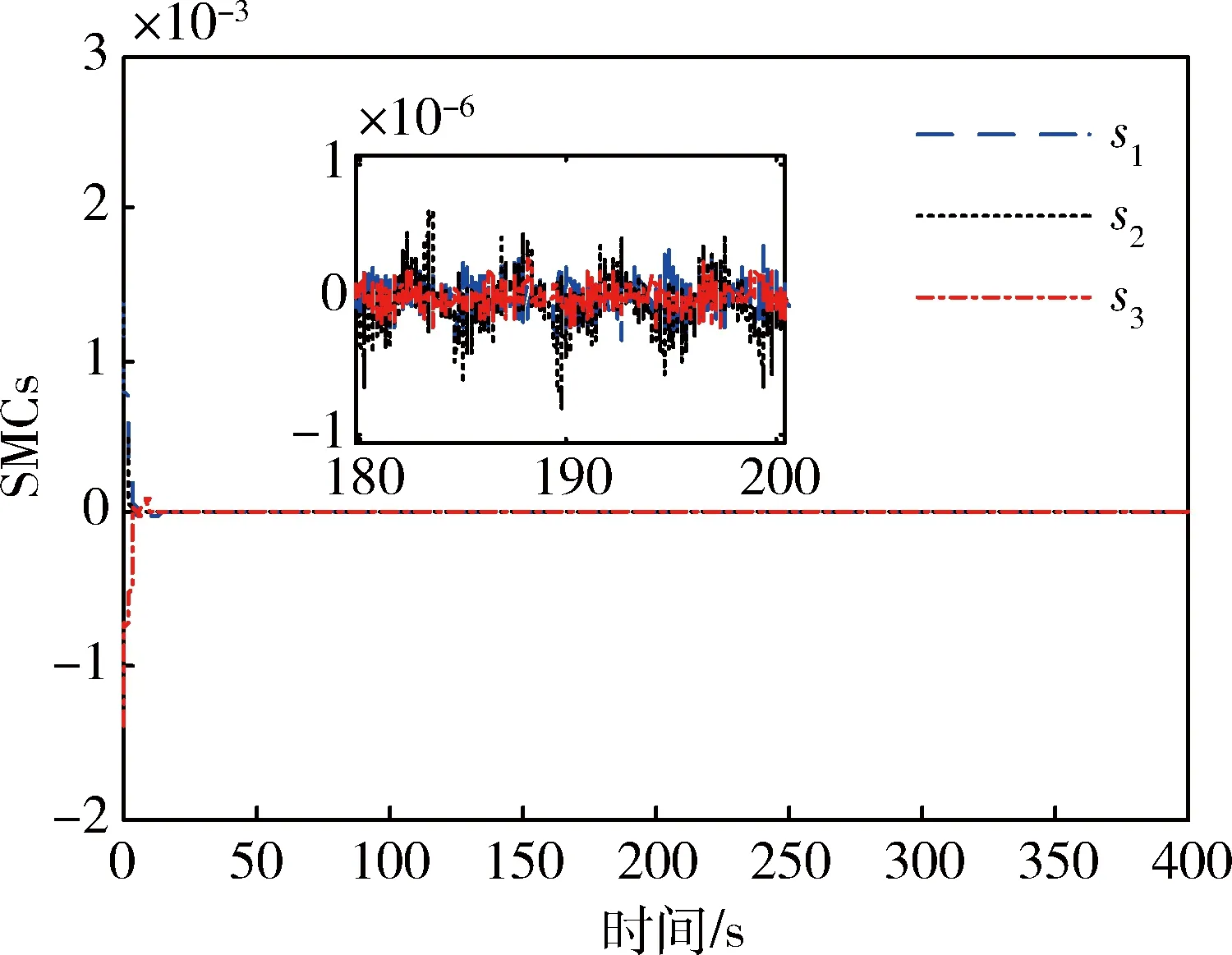
图8 SMC滑模面变化曲线Fig.8 Time responses of sliding mode surface by SMC

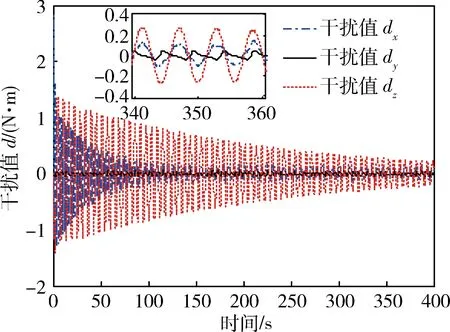
图9 干扰力矩变化曲线Fig.9 Time responses of disturbance

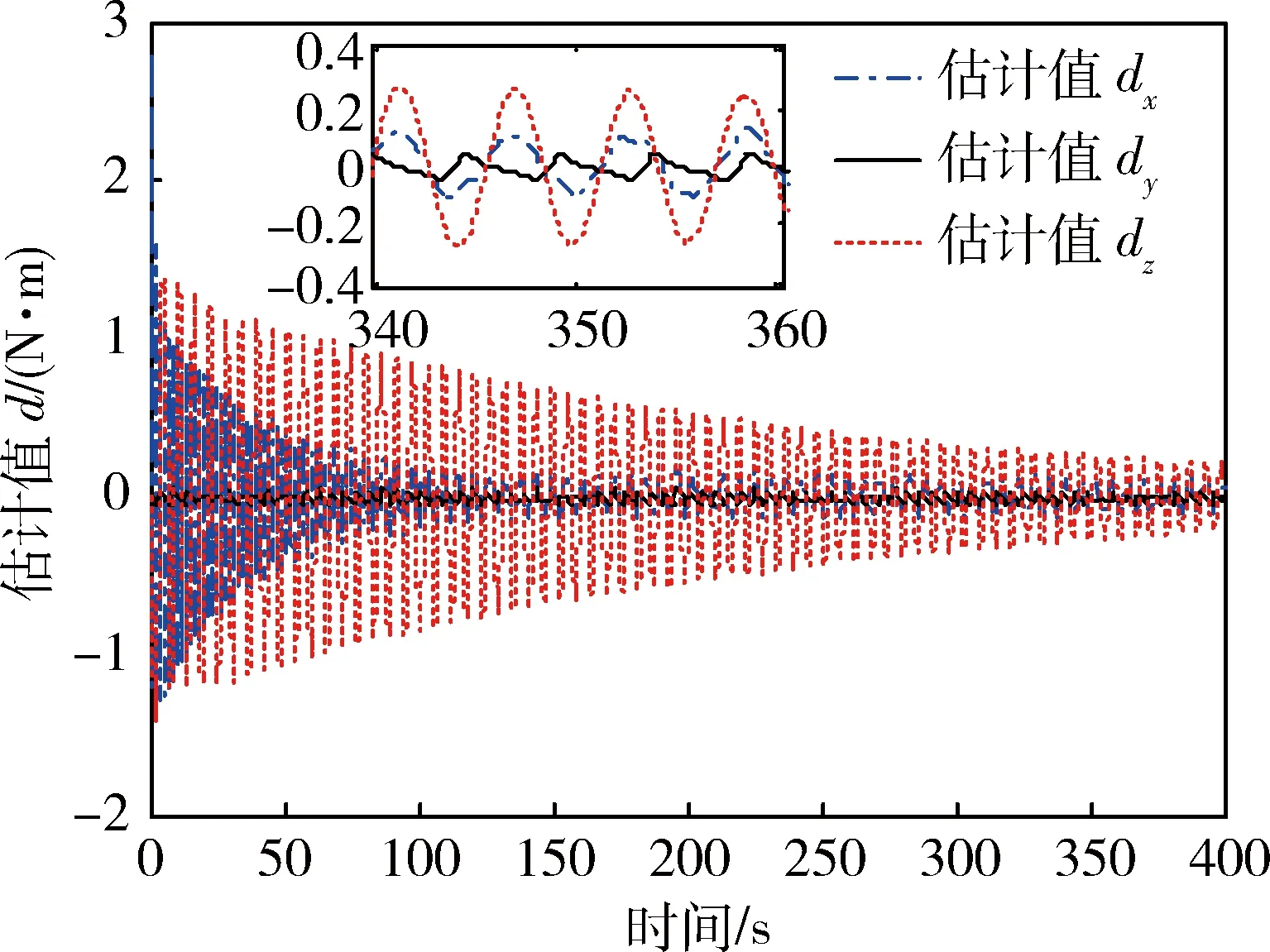
图10 干扰力矩估计曲线Fig.10 Time responses of disturbance estimation

图11 干扰力矩估计误差曲线Fig.11 Time responses of disturbance estimation error

4 结 论

本文针对带挠性太阳帆板的卫星姿态控制系统，设计了基于干扰观测器的滑模变结构控制器.干扰观测器用于估计系统中存在的内外干扰，并进行前馈补偿，滑模变结构控制器进一步抑制干扰，既减弱了颤振现象，又能有效实现卫星姿态与角速度的渐进收敛.仿真结果表明，所设计的控制系统有效提高了挠性卫星姿态控制性能.

[1] WANG Z, WU Z. Nonlinear attitude control scheme with disturbance observer for flexible spacecrafts[J]. Nonlinear Dynamics, 2015, 81(1-2): 257-264.

[2] KIDA T, YAMAGUCHI I, CHIDA Y, et al. On-orbit robust control experiment of flexible spacecraft ETS-VI[J]. Journal of Guidance, Control and Dynamics. 1997, 20(5): 865-872.

[3] 宗红, 张洪华, 徐福祥. 挠性卫星自适应姿态跟踪控制[J]. 中国空间科学技术, 2007, 27(6): 25-30. ZONG H, ZHANG H H, XU F X. Adaptive attitude tracking control of flexible satellite[J]. Chinese Space Science and Technology, 2007, 27(6): 25-30.

[4] 张洪华, 张国峰. 带有挠性附件卫星的自适应内模控制[J]. 空间控制技术与应用, 2001，27(3): 10-16. ZHANG H H, ZHANG G F. Adaptive internal model control for satellite with flexible appendages[J]. Aerospace Control and Application, 2001(3): 10-16.

[5] 朱承元, 杨涤, 杨旭. 大挠性多体卫星的自抗扰姿态控制系统设计[J]. 航天控制, 2004, 22(6): 25-31. ZHU C Y, YANG D, YANG X. Design of active disturbance rejection attitude control system for large flexible multi-body satellite[J]. Aerospace Control, 2004, 22(6): 25-31.

[6] 李新国, 陈士橹. 挠性卫星太阳帆板的变结构主动控制[J]. 西北工业大学学报, 1997, 15(1): 84-87. LI X G, CHEN S L. Variable structure active control of flexible satellites with solar paddles[J]. Journal of Northwestern Polytechnical University, 1997, 15(1): 84-87.

[7] HU Q, MA G. Variable structure control and active vibration suppression of flexible spacecraft during attitude maneuver[J]. Aerospace Science and Technology, 2005, 9(4): 307-317.

[8] 秦浩. 带柔性太阳帆板的航天器姿态控制实验研究[D]. 北京: 北京理工大学, 2015. QIN H. Experimental study on the attitude control of spacecraft with flexible solar arrays[D]. Beijing: Beijing Institute of Technology, 2015.

[9] 吕建婷, 李传江, 马广富. 卫星姿态调节的滑模PID控制器设计[J]. 哈尔滨工业大学学报, 2008, 40(7):1009-1012. LV J T, LI C J, MA G F. A sliding mode PID controller design for satellite attitude regulation[J]. Journal of Harbin Institute of Technology, 2008, 40(7):1009-1012.

[10] 毕开波, 孙剑, 隋先辉. 基于干扰观测器的天基观测航天器姿态控制设计[J]. 海军航空工程学院学报, 2016, 31(1): 17-21. BI K B, SUN J, SUI X H. Design of attitude control system of space-based observation spacecraft based on disturbance observer[J]. Journal of Naval Aeronautical and Astronautical University, 2016, 31(1): 17-21.

[11] 陆栋宁, 刘一武. 基于内模原理的复杂挠性卫星姿态控制研究[J]. 宇航学报, 2014, 35(3): 306-314. LU D N, LIU Y W. Research on internal model principle based attitude controlfor complex flexible satellites[J]. Journal of Astronautics, 2014, 35(3): 306-314.

[12] 章仁为.卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 1998.

[13] 靳潇潇. 挠性航天器姿态抗干扰控制[D]. 北京: 北京航空航天大学, 2015. JIN X X. Anti-disturbance attitude control of flexible spacecrafts[D]. Beijing: Beihang University, 2015.

[14] 张猛, 祝晓丽, 陆娇娣,等. 一种高稳定度太阳帆板驱动机构控制方法[J]. 空间控制技术与应用, 2010, 36(4): 46-49. ZHANG M, ZHU X L, LU J D, et al. A high stability control method for solar array drive mechanism[J]. Aerospace Control and Application, 2010, 36(4): 46-49.

[15] 斯祝华, 刘一武, 黎康. 太阳帆板驱动装置建模及其驱动控制研究[J]. 空间控制技术与应用, 2010, 36(2): 13-19. SI Z H, LIU Y W, LI K. Research on modeling and driver design of solar array drive assembly[J]. Aerospace Control and Application, 2010, 36(2): 13-19.

[16] 朱仕尧, 雷勇军, 谢燕,等. 高精度航天器太阳能电池阵减扰驱动方法[J]. 振动与冲击, 2014, 33(21): 26-30. ZHU S Y,LEI Y J, X Y, et al. Disturbance-mitigation drive methods for solar array of a high-precision spacecraft[J]. Journal of Vibration and Shock, 2014, 33(21): 26-30.

[17] ZHU S, LEI Y. Disturbance analysis and feed-forward compensation for the flexible solar array sun-tracking drive[J]. Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2015, 229(14)：71-76.

[18] CANUDASD W C, OLSSON H, ASTROM K J, et al. A new model for control of systems with friction[J]. IEEE Transactions on automatic control, 1995, 40(3): 419-425.

[19] LIU H, GUO L, ZHANG Y M. An anti-disturbance PD control scheme for attitude control and stabilization of flexible spacecrafts[J]. Nonlinear Dynamics, 2012(67): 2081-2088.

[20] 王振. 空天飞行器复合控制技术研究[D]. 北京: 北京航空航天大学, 2015. WANG Z. On composite control of aerospace vehicles[D]. Beijing: Beihang University, 2015.

[21] TADIKONDA S S K. Articulated, flexible multibody dynamics modeling: geostationary operational environmental satellite-8 case study[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(2): 276-283.

Attitude Control of Flexible Satellites via Disturbance-Observer-BasedSliding Mode Controller

WANG Xuebing, WU Zhong

(SchoolofInstrumentationScienceandOpto-ElectronicsEngineering,BeihangUniversity,Beijing100191,China)

To mitigate the effect of diverse internal and external disturbances of flexible spacecraft on attitude control performance, a composite control scheme is proposed by combining disturbance-observer (DO) and sliding mode control (SMC). The disturbance observer can observe the disturbances and output the estimation, which can be compensated through feedforward. Then, SMC is used to suppress the uncompensated disturbances, so that the attitude and rate of the spacecraft are asymptotically converged. Compared with conventional SMC, the proposed DO+SMC approach just need a smaller switching gain to restrain the remaining disturbances that the DO does not compensate, and the chattering is attenuated effectively. Simulation results demonstrate the feasibility of the designed controller.

flexible spacecraft; attitude control; disturbance observer; sliding mode control

资助项目(10772011). 收稿日期：2017-01-04

V448.2

A

1674-1579(2017)02-0036-07

10.3969/j.issn.1674-1579.2017.02.006

王雪冰(1990—)，女，硕士研究生，研究方向为航天器姿态控制技术；吴 忠(1970—)，男，教授，研究方向为航天器姿态控制、伺服控制技术等.