基于神经网络的自由漂浮空间机械臂自适应鲁棒控制*

王 超，江 洁，林森海，张文辉,，陈荣昌

(1.丽水学院 工学院，丽水 323000； 2.浙江斯凯瑞机器人股份有限公司，丽水 323000)



基于神经网络的自由漂浮空间机械臂自适应鲁棒控制*

王 超1，江 洁1，林森海2，张文辉1,2，陈荣昌2

(1.丽水学院 工学院，丽水 323000； 2.浙江斯凯瑞机器人股份有限公司，丽水 323000)

针对自由漂浮空间机械臂动力学模型难以精确获得，且无法表达为关于未知参数的线性形式问题，提出基于自适应神经网络的鲁棒控制方法.对于不确定性空间机械臂系统模型中存在的未知不确定部分，利用神经网络的万能逼近特性，设计神经网络控制器来补偿未知模型，避免传统控制中的保守上界估计；采用泰勒线性化技术将神经网络隐含层中的高斯函数线性化，设计包括网络权值、高斯中心及宽度在内的网络全参数自适应学习律，实现在线实时调整，提高控制精度；设计鲁棒自适应控制器来抑制外界扰动，并补偿逼近误差，提高系统鲁棒性；基于Lyapunov理论证明闭环系统的一致最终有界(UUB).仿真试验表明所提控制方法能够获得较好控制效果，对空间机械臂控制具有一定工程应用价值.

空间机械臂；神经网络；鲁棒控制；自适应控制；一致最终有界

*浙江省自然科学基金(LY14F030005)，浙江省科技厅项目(2015C31160)，浙江省教育厅项目(Y201534043)(Y201636936)，丽水市高层次人才资助项目(2015RC04)和丽水市科技计划项目(2015KCPT03).
收稿日期：2016-08-15

0 引 言

空间机械臂在空间站建造全过程担负着搬运、装卸、安装等极其重要的工作，并能代替宇航员去完成其他各类危险的空间任务.火星探测车安装的机械臂担负着火星表面及深层土壤的勘探取样等工作.外界工况不仅对空间机械臂控制系统造成干扰，而且自由漂浮空间机械臂自身的运动必然引起载体的耦合运动，所以其动力学与控制问题远较地面机械臂复杂，特别是受到当前测量水平限制、测试误差、机械臂制造精度、减速机构齿轮间隙等因素的影响[1-2]，无法获得精确的数学模型.这些均对空间机械臂的高精度控制提出了挑战，因此对空间机械臂控制技术进入深入研究具有重要意义[3].

针对上述问题，国内外学者对此进行了一系列研究.文献[4]提出载体位置、姿态均不受控的飘浮基空间机器人Terminal滑模控制方案.文献[5]采用滑模变结构方法解决自由漂浮状态空间机器人实时控制问题.

由于神经网络具有较好的非线性逼近能力，近年来对基于神经网络的空间机器人控制研究成为热点[6].文献[7]提出基于神经网络的空间机械臂控制方法，该方法不需要测量、反馈载体位置、移动速度和移动加速度信号，样本训练对于控制精度有较大影响，属于自学习控制类型.自适应控制由于能够保证控制系统稳定性，近年来成果较多[8-9].文献[10] 针对空间机械臂摩擦死区非线性问题，提出基于神经网络的补偿控制策略.文献[11]针对空间机械臂模型未知不确定部分提出基于神经网络自适应控制方法.文献[12]针对外界干扰问题，提出基于神经网络的鲁棒控制方案，采用神经网络对干扰及摩擦等参数变化部分模型进行补偿达到较高控制精度.文献[13]针对末端质量突变工况，提出具备冗余控制能力的神经变结构控制方法，保证神经网络控制失效情况下的稳定性.文献[14]针对机械臂接触环境未知情况，提出一种神经网络自适应力控制方法，采用神经网络来估计机器人的未知模型矩阵.

上述成果采用径向基神经网络的逼近特性，实现了不确定模型的补偿，但自适应学习算法仅仅针对网络权值参数.实际上，径向基神经网络的隐函数层参数(高斯函数的中心参数和宽度参数)，对网络泛化能力也起着重要作用，对控制精度有着较大影响.面向模型不确定及外界干扰的自由漂浮空间机械臂系统，提出包括高斯函数中心参数、宽度参数和权值参数在内的网络全参数自适应学习算法和鲁棒控制策略.建立不确定性空间机械臂动力学模型，利用径向基神经网络优秀的逼近能力，补偿未知不确定模型；针对网络隐层高斯函数的连续非线性特点，采用泰勒技术对进行参数线性化，设计包括高斯函数中心、宽度及权值的全参数自适应学习律，实现在线实时调整；设计自适应鲁棒控制器抑制外界扰动，并补偿逼近误差；基于Lyapunov 理论证明了整个闭环系统信号一致最终有界(UUB).仿真试验结果表明该控制方法的有效性.

1 自由漂浮空间机械臂动力学方程

空间机械臂处于微重力环境中时，基座不固定，对于n关节机械臂来说，系统共有n+6个自由度，当机械臂运动时，基座位姿改变，根据拉格朗日法得到n关节空间机械臂动力学方程为[8-10]

(1)

若空间机器人处于自由漂浮状态，则基座位姿不受控制，即β6×1=0.系统不受其他外力或力矩作用，根据动量矩守恒定律，漂浮空间机器人动力学方程如下[7-9]：

(2)

空间机器人动力学方程具有如下性质[7-9]：

性质1.惯性矩阵M(qm)是对称正定矩阵.

2 自适应神经网络的鲁棒控制器设计

定义qr为参考轨迹，则

(3)

联立式(2)、(3)可得闭环系统误差方程为：

(4)

如果不存在测量误差及主观因素等，假设机械臂模型建模能够精确获得，同时d=0.则设计如下控制律可保证闭环系统全局渐进稳定:

(5)

其中，Kv为正定矩阵.

但在实际工程中，不仅需要考虑外界干扰d≠0的情况，而且无法获得空间机械臂精确模型，由误差方程(4)得系统不确定模型

(6)

假设不确定项f通过其他手段能够精确获得，则修正的控制律为

τ=f+Kvs

(7)

取Lyapunov函数为

(8)

即，系统稳定.

因此为保证控制系统稳定，需要在实际工程中完成对建模不确定部分f的精确补偿.

由于径向基神经网路(RBFNN)具有万能逼近特性，且属于局部泛化网络，拥有较快学习速度，并可以避免局部极小问题[8]，可以考虑采用该类神经网络实现对不确定部分f逼近补偿.

图1 径向基神经网络结构Fig.1 Radial basis function neural network

考虑到神经网络存在的逼近误差以及非参数不确定，对控制律(7)进行修正：

(9)

(10)

(11)

式中，X=[x1,…,xm]T为网络的输入向量，cj=[cj1,…,cjm]是第j个节点的中心矢量，σj表示节点j的基函数宽度.

由图1径向基神经网络结构可知，RBF神经网络属于三层前向网络，其中RBF作为隐单元的“基”构成隐层空间，将输入矢量直接映射到隐空间，当RBF的中心c与宽度σ确定后，映射关系也就确定了，而隐层与输出层之间属于线性关系，这样最终输出就确定了.

传统RBF神经网络控制中，RBF基函数的中心c与宽度σ是假设的常数，其映射关系是确定的，难以获得最佳映射输出，本文考虑到这种情况，拟采用线性化技术获得可调的中心c与宽度σ自适应学习律，从而达到最优输出.

则神经网络的理想逼近为

f=θ*Tφ(x,c*,σ*)+ε

(12)

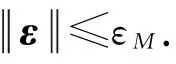
(13)

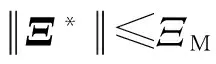
(14)

定义

(15)

则式(14)可写为

(16)

考虑到控制精度与神经网络泛化性相关，为提高控制精度，对网络隐层节点处的高斯基函数进行线性化处理，以便实现网络全参数学习律在线实时调整，提高泛化能力.

(17)

则由式(15)～(17)得

(18)

(19)

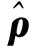
(20)

RBF神经网络权值及参数自适应学习算法为

(21)

(22)

(23)

式中：K1、K2、K3为正对角阵；λ是正常数.

3 基于Lyapunov的控制系统稳定性证明

定理.对漂浮空间机械臂系统(2)，采用控制律 (9)，鲁棒控制器(20)，自适应控制律 (21)～(23)，定义Lyapunov函数可以证明控制系统一致最终有界(UUB).

(24)

对其进行微分得

(25)

(26)

将控制律式(9)代入式(26)得闭环系统误差方程最终修正式为

(27)

则将误差方程式(27)代入式(25)得

(28)

应用性质2将式(18)及自适应学习算法(21)～(23)代入得

(29)

(30)

(31)

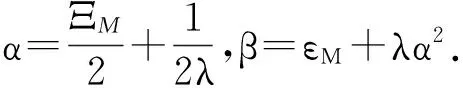
只要

(32)

则

(33)

4 仿真算例及分析

4.1 模型参数定义

以自由漂浮两连杆空间机械臂为仿真模型来验证所提的控制方案的有效性，具体参数物理意义如表1所示.

表1 两自由度空间机械臂参数Tab.1 Two degree of space manipulators parameters

假设建模误差及外部干扰:

期望的轨迹:

q1d=sin2t+sin3t，q2d=cos2t+cos4t.

控制器增益及参数:

Kv=diag{20,20}，λ=0.6，γ=50，Λ=diag{5,5}.

关节初始状态：q1(0)=q2(0)=0.

这里设定神经网络初始权值为0，各基函数宽度及基函数中心在输入输出域中随机选取，隐层节点数设置为30.

4.2 仿真试验对比与分析

通过与文献[11]对比分析来说明所提方法的优越性.文献[11]中同样采用自适应神经网络控制方法，其具体控制策略如下：

总控制律：

本文设计思路主要考虑到径向基函数神经网络的泛化能力不仅与网络权值有关，而且隐含层高斯函数对网络泛化能力也具有重要影响，仿真试验结果见图2.

由图2可以看出，两种算法均能在初始误差较大的情况下准确跟踪期望轨迹，但文献[11]约在1.5 s内能较好跟踪期望轨迹，神经网络约在1.5 s时能较好逼近非线性不确定模型，而本文所提出控制方法约在0.5 s内完全跟踪期望轨迹，神经网络在不到1 s内很好逼近非线性不确定模型获得较好补偿效果，控制精度较高.同时，本文方法输出力矩较小.

试验分析表明：神经网络泛化能力不仅与网络权值有关，隐层参数对其也有重要影响.隐层参数(高斯中心、宽度)自适应律设计不仅能够大幅提高神经网络的逼近精度和速度，且其非线性逼近特性使得控制力矩输出较优，进而降低控制力矩，节省燃料，对于空间机械臂控制具有重要意义.

5 结 论

针对自由漂浮空间机械臂动力学模型难以精确获得，且无法表达为关于未知参数的线性形式问题，提出基于自适应神经网络的鲁棒控制方法.

(1)针对空间机械臂动力学模型中的未知不确定部分，设计神经网络控制器来补偿系统中的不确定模型，避免传统控制中的保守上界估计；

(2)采用泰勒线性化技术将神经网络隐含层中的高斯函数线性化，设计包括网络权值、高斯中心及宽度在内的网络全参数自适应学习律，实现在线实时调整，提高控制精度；

(3)针对外界扰动和逼近误差，设计自适应鲁棒控制器，提高系统鲁棒性.

基于Lyapunov理论证明了闭环系统的一致最终有界(UUB).仿真证明了所提控制方法的有效性，对当前中国空间机械臂控制提供借鉴.

图2 仿真结果Fig.2 Simulation results

[1] 刘福才, 高娟娟, 王芳. 地面装调的空间机械臂在空间应用时的自适应鲁棒控制[J].控制理论与应用，2013，30(1)：69-75. LIU F C, GAO J J. WANG F. Adaptive robust control for the space application of manipulator aligned on ground[J].Control Theory & Applications, 2013，30(1)：69-75.

[2] CHEAH C C，KAWAMURA S，ARIMOTO S，et al. H∞tuning for task-space feedback control of robot with uncertain Jacobian matrix[J]. IEEE Trans. on Automatic Control， 2001，46 (8):1313-1318.

[3] ZHANG W, YE X, JI X. RBF neural network adaptive control for space robots without speed feedback signal[J]. Transactions of the Japan Society for Aeronautical & Space Sciences, 2013, 56(6):317-322.

[4] 于潇雁，陈力. 载体位置、姿态均不受控的飘浮基柔性空间机器人的Terminal滑模控制[J].中国机械工程，2015，26(7): 938-945. YU X Y, CHEN L.Terminal sliding mode control of a free-floating flexible space robot[J].China Mechanical Engineering ，2015，26(7): 938-945.

[5] KHALOOZADEH H，HOMAEINEJAD M R. Real-time regulated sliding mode controller design of multiple manipulator space free-flying robot[J]. Journal of Mechanical Science and Technology，2010，24(6):1337-1351.

[6] 张文辉，叶晓平，季小明，等.国内外空间机器人技术发展综述[J].飞行力学，2013，31(3)：198-202. ZHANG W H, YE X P , JI X M, et al. Development summarizing of space robot technology national and outside[J]. Flight Dynamics, 2013，31(3)：198-202.

[7] 洪昭斌, 陈力. 基于高斯基模糊神经网络的漂浮基柔性空间机械臂自学习控制[J]. 工程力学, 2009, 26(6):172-177. HONG Z B,CHEN L.Self-learning control of space flexible manipulator based on Gauss function fuzzy neural network[J].Engineering Mechanics,2009, 26(6):172-177.

[8] HU H，WOO P Y. Fuzzy supervisory sliding-mode and neural-network control for robotic manipulators[J].IEEE Trans. Ind. Electron，2006，53(3):929- 940.

[9] LIU H, ZHANG T. Adaptive neural network finite-time control for uncertain robotic manipulators[J]. Journal of Intelligent & Robotic Systems, 2014, 75(3):363-377.

[10] HE W, DAVID A O, YIN Z, et al. Neural network control of a robotic manipulator with input deadzone and output constraint[J]. IEEE Transactions on Systems Man & Cybernetics Systems, 2016, 46(6):759-770.

[11] 谢箭，刘国良，颜世佐，等. 基于神经网络的不确定性空间机器人自适应控制方法研究[J]. 宇航学报，2010， 31(1): 123-129. XIE J, LIU G L,YAN S Z, et al. Study on neural network adaptive control method for uncertain space manipulator[J].Journal of Astronautics, 2010，31(1): 123-129.

[12] NGO T Q, WANG Y N, MAI T L, et al. Robust adaptive neural-fuzzy network tracking control for robot manipulator[J]. International Journal of Computers Communications & Control, 2014, 7(2):341-352.

[13] ZHANG W H, QI N M, MA J, et al. Neural integrated control for a free-floating space robot with suddenly changing parameters[J]. Science China Information Sciences, 2011, 54(10):2091-2099.

[14] LEE C H, WANG W C. Robust adaptive position and force controller design of robot manipulator using fuzzy neural networks[J]. Nonlinear Dynamics, 2016, 85(1):1-12. 作者简介：王 超(1979—)，女，讲师，研究方向为机器人控制与机电一体；江 洁(1981—)，女，讲师，研究方向为机器人动力学与装备；林森海(1967—)，男，高级工程师，研究方向为机器人系统集成技术；张文辉(1980—)，男，副教授，研究方向为机器人控制与智能系统；陈荣昌(1965—)，男，高级工程师，研究方向为机电一体化与制造.

Adaptive Robust Control Method of Free-Floating SpaceManipulators Based on Neural Network

WANG Chao1, JIANG Jie1, LIN Senhai2， ZHANG Wenhui1,2， CHEN Rongchang2

(1.SchoolofEngineering，LishuiUniversity，Lishui323000，China;2.ZhejiangSkerryRobotCo.,LTD，Lishui323000，China)

Trajectory tracking control problems of free-floating space manipulators with uncertainty are considered, and a robust adaptive control method is put forward based on neural network. The dynamics model of uncertain space manipulators is established, and the unknown nonlinear parts of system model are considered. A neural network controller is designed to approach the unknown uncertain parts, by the way the traditional upper bound of conservative is be avoided estimating. Taylor technology is used to linearize the Gaussian function of neural network hidden layer. Then the adaptive learning laws of the network weight parameters, the hidden layer center and width of Gaussian function are designed to guarantee the online real-time adjustment. The robust adaptive controller is designed to compensate the amount of high-order item and the approximation errors for better control accuracy. The uniformly ultimately bounded (UUB) of the closed-loop system is proved based on the Lyapunov theory. Simulation results show that the proposed control method can get better control accuracy, and the controller has important engineering value for the space manipulator.

space manipulator； neural network; robust control; adaptive control； uniformly ultimately bounded

TP24

A

1674-1579(2017)02-0007-06

10.3969/j.issn.1674-1579.2017.02.002