混频前端抽取FFT伪码并行捕获算法

卢 迪, 郑世超

(哈尔滨理工大学电气与电子工程学院, 哈尔滨 150080)

0 引言

北斗卫星导航系统(beidou navigation satellite system,BDS)是中国自主建设、独立运行、世界上首个集定位、授时和报文通信为一体的卫星导航系统,是继美国GPS、俄罗斯格洛纳斯GLONASS、欧洲伽利略GALILEO之后,为全球用户提供全天候、全天时、高精度定位、导航和授时服务的国家重要空间基础设施。建设北斗卫星导航系统,对于提高我国国际地位,促进经济发展,保障国家安全等方面,都具有重大战略意义。

北斗卫星导航信号采用码分多址(CDMA)调制方式,不同的伪随机码对不同卫星的导航数据进行扩频调制[1]。为了跟踪并解码北斗信号,获得导航信息,首要任务是捕获信号。若要完成信号捕获,必须让接收机生成的伪随机码与卫星信号一致,再调整其码相位和多普勒频率,直到与卫星信号一致。因此捕获过程可看作是对可见卫星信号的载波多普勒频率和码相位粗略估计值的二维搜索[2-4]。

传统的时域串行捕获算法是一种硬件实现容易但捕获速度最慢的搜索方法,不能够满足高动态下实时位置的解算,低信噪比情况下可能丢失数据。匹配滤波器捕获算法虽捕获速度较快,但其实现电路复杂,仅适用于短周期的PN码捕获。基于FFT的伪码并行捕获算法利用FFT进行频域分析,将传统的二维搜索变成一维搜索,使得捕获速度得以显著提高[5-7]。

1 基于FFT的伪码并行捕获原理

北斗卫星信号是扩频信号,只有利用扩频码良好的自相关特性和较差的互相关特性才能从噪声中提取出卫星信号。卫星信号经过天线、低噪声放大器、射频前端、AD采样后得到的数字中频信号表示如下:

xk(n)=ACk(n)Dk(n)cos[2π(fc+fd)nT+φ]+e(n)

(1)

式中:k表示卫星编号;A表示信号幅度;C(n)表示伪码;D(n)表示伪码上调制的数据码;fc表示载波中频;fd表示载波多普勒频率;T为采样时间;φ为输入载波与本地载波的相位差;e(n)是均值为0、方差为1的高斯白噪声。

传统的时域串行捕获算法如图1所示,其基本原理是:在确定的一段频率范围内,按照某种规则将频率划分为若干段,从第一频段开始,滑动本地伪码,依次做对应该频段的所有不同码相位的相关积分,然后调整到下一频段,搜索直至遍历了所有的频率和码相位为止,最后对所有相关积分结果做阈值判断[8]。如果相关峰值大于捕获门限,表示捕获到卫星,并记录下峰值所对应的频率和码相位。否则,表示当前接收到的卫星信号伪码和本地假设的卫星信号伪码不匹配,控制逻辑需改变本地伪码进行再次搜索。

由于时域串行捕获算法的搜索时间长,因此引入了基于FFT的伪码并行捕获。该算法原理是建立在时域的卷积等效于其频域的傅里叶变换乘积的基础上[9],不过卫星信号捕获时用到的是相关运算,不是卷积运算,但该过程也可由傅里叶变换表示。

两个长度为N的有限序列x(n)与y(n)之间的相关表示为:

(2)

而x(n)与y(n)的循环卷积表示为:

⊗y(n)

(3)

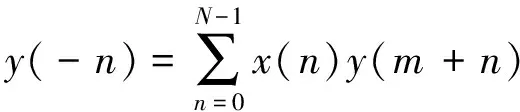
(4)

因此:

rxy(m)=x(n)⊗y(-n)

(5)

式中m取[0,1,2,…,N-1]。⊗表示循环卷积运算符。

因时域的卷积等效于频域的乘积,故对式(5)两边同时做FFT变换,可得:

R(k)=X(k)Y*(k)=X*(K)Y(k)

(6)

然后对上述结果进行傅里叶逆变换(IFFT):

r(m)=IFFT(FFT(y(n))·CONJ(FFT(x(n))))

(7)

最后对所得结果逐个求模,即得到接收信号与本地参考信号的相关值,然后进行阈值判断。

北斗卫星B1频段I支路伪码码速率是2.046 Mcps,显然,这种算法使得原本对应一个频率点需寻找2 046次码相位操作变为只需执行两次FFT,一次乘法以及一次IFFT运算,便可以得到相关数据,大大减少了运算量,提高了捕获速度[10]。该算法的实现原理框图如图2。

2 改进的混频前端抽取FFT伪码并行捕获算法

在基于FFT的伪码并行捕获算法中,N点FFT共需(N/2)·log2N次复数乘法和Nlog2N次复数加法,N越大,算法的运算复杂度越大。如果采用11.999 MHz的中频采样时钟,那么1 ms的中频采样数据x(n),n=0,1,…,11 998,与本地产生的正弦、余弦信号相乘进行载波分离,将得到11 999点的正交I、Q信号。之后需要对这11 999点的输入信号x(n)和本地产生的伪码信号y(n),n=0,1,…,11 998,做两次FFT和一次IFFT。对于强信号而言,1～2 ms的捕获数据就够了,但是对于低信噪比环境下的弱信号而言,往往需要3～10 ms的捕获数据,而11 999不是2的整次幂,运算过程会涉及到补零或FFT的多基运算,这会带来运算量的加大和复杂度的提升,捕获速度也会相应变慢。基于上述原因,文中采用混频前端抽取FFT捕获的方法,在不影响频率分辨率的前提下,通过减少采样数据来换取速度的提升,其捕获原理框图如图3所示。

北斗卫星信号采用的伪码为Gold码,序列长度2 046,基于FFT的伪码并行捕获算法需要每毫秒从2 046个伪码上采样到11 999个点,文中采用每5个点抽取一个,相对传统算法仅需采样2 400个点,相应地本地伪码输出也减少到2 400个。由于2 400大于2 046,说明这2 400个点包含一个完整的伪码周期,不会带来信息的损失,这样在信号捕获时,能够保证每一个码相位都能被搜索到,从而得到准确的捕获结果。

然而采样点数的大大减小,在带来捕获速度提升的同时,也带来了相关能量幅值的降低,这样在阈值检测环节,会导致误判的可能,在信号较弱的情况下,甚至会出现漏捕,降低发现卫星信号的概率。解决该问题首先想到的方法是延长捕获时间,增加FFT运算长度,而这又势必会导致运算量的增加和系统复杂度的提升。因此需要解决在不增加系统复杂度的前提下,达到弥补信号相关能量幅值损失的目的。文中考虑把连续M个伪码周期时间段内的FFT伪码并行搜索结果进行累加,从而使得FFT的相关输出R(k)的能量幅值增加。设第i个伪码周期时间段内FFT伪码并行搜索结果为[Ri(0),Ri(1),…,Ri(2 399)].则M个伪码周期的时间段内FFT搜索结果为:

(8)

最后是对所有的|Rsum(n)|2(n=0,1,…,2399)进行峰值检测。由于累加的结果,使得信号的能量幅值得以提升,虽然牺牲了一定的捕获时间,但提高了发现信号的概率。

3 仿真与分析

北斗信号捕获的模拟用于信号处理的重要参数包括:采样频率fs=11.999 MHz,载波中频fc=3.56 MHz,采样时间为一个C/A码周期T=1 ms,多普勒频率的变化范围是±10 kHz,频率步进500 Hz。采样数据存储在计算机里,仿真通过安装在主频为3.30 GHz、内存为4 GB的64位计算机上的MATLAB(R2013a)仿真软件进行模拟捕获。根据信噪比的计算公式:

SNR=10Lg(Ps/Pn)

(9)

式中Ps和Pn分别代表信号和噪声的有效功率。噪声是均值为0、方差为1的高斯白噪声。可仿真出不同信噪比下的数字中频信号。

为了检测文中算法的正确性,图4给出了3种捕获结果对比图。图4(a)是利用FFT直接求11 999点的三维捕获图,图4(b)是经过混频前端抽取的2 400点捕获图,图4(c)是混频前端抽取后积分累加3个伪码周期(以下简称积分累加)的捕获图,其中X轴代表北斗卫星信号伪码的2 046个码相位,Y轴表示±10 kHz频移范围的多普勒频率,Z轴表示相关幅值。在SNR=-15 dB的情况下,3种方法均可见卫星信号,且能基本正确地捕获到卫星信号的码相位640chip和多普勒频率2 000 Hz。

图5给出了3种算法的码相位和相关幅值的二维关系图。图5(b)能明显看到在峰值周围存在一些幅值较大的干扰点,这对阈值检测很不利。而图5(c)的改进算法中,可以很直观的看到峰值相比于其他点较突出,去除了周围的干扰点,有利于捕获。就相关幅值而言,3种算法的相关幅值数量级分别是106、104和105。混频前端抽取FFT算法的峰值是非峰值的2倍左右,而积分累加算法的峰值与非峰值比接近7。虽然积分累加算法在相关幅值方面低于传统FFT算法,但其突出的峰值已能满足捕获条件,效果也较明显。

3种算法的捕获时间和捕获精度情况如表1。文中分别在信噪比SNR=-15 dB和SNR=-20 dB环境下,对3种基于FFT的捕获算法各做了30组实验,通过统计计算,得出捕获时间和捕获精度。由于卫星信号捕获获得的只是粗估计值,下一步的跟踪过程将进一步提高多普勒频率和码相位的估计精度。所以捕获得到的结果允许在真值附近有一定的浮动。文中实验结果允许码相位有1 chip的偏差,即码相位结果639 chip、640 chip和641 chip均视为捕获成功,载波多普勒频率必是2 000 Hz。文中定义捕获精度为:

(10)

表1 3种算法捕获结果对比

从表中可见,传统FFT捕获算法捕获精度近乎100%,但捕获时间长,不满足高动态情况下位置解算和实时更新的需求。而混频前端抽取的FFT捕获算法在SNR=-15 dB的情况下,捕获速度最快,但捕获精度最低,虽对于粗捕获而言,该精度也满足要求,但是随着信噪比的降低,捕获精度直降至0%,可见该算法的系统稳定性太差。积分累加FFT捕获算法,时间虽比混频前端抽取FFT算法增加了3倍左右,但相比传统FFT捕获算法还是大大缩短了,且捕获精度也有所保证,在SNR=-20 dB时,依然具有良好的捕获性能。因此,改进算法更适合在环境较恶劣的情况下实现快速捕获。

4 结束语

文中提出了一种新的基于FFT的伪码并行捕获算法,降低了硬件复杂度,减少了系统运算量。仿真结果表明,文中提出的算法,能够准确捕获到北斗卫星信号,并且实现了捕获速度和捕获精度的平衡,在信噪比降低的情况下,能够保证捕获速度几乎不变,捕获精度维持在80%左右的水平,使系统能在高动态下实现稳定、实时、高效的运行。在实际应用中具有可操作性。但由于伪码并行捕获算法对多普勒频率采用串行搜索,此时多普勒频移粗估计误差为正负半个频率搜索步进,如何进一步细化多普勒估计值将是后续研究的方向。

参考文献:

[1] MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Initial assessment of COMPASS/BeiDou-2 regional navigation satellite system [J]. GPS Solutions, 2013, 17(2): 211-222.

[2] 陈希, 张锐, 帅涛. 基于FFT的GPS快速并行捕获算法 [J]. 宇航学报, 2011, 32(1): 162-166.

[3] TANG B, LIU S S, TANG W T, et al. Design a L1 software GPS receiver based on IF GPS signal simulator [C]∥IEEE. Proceedings of 2006 8th International Conference on Signal Processing. [S.l.]: IEEE, 2006:2270-2273.

[4] 李怀建, 刘莉, 杜小菁. 高灵敏度GPS信号捕获技术研究 [J]. 弹箭与制导学报, 2009, 29(4): 25-28.

[5] 刘天旻. 北斗卫星导航系统B1频段信号分析研究 [D]. 上海: 上海交通大学, 2013.

[6] CHAWLA K K, SARWATE D V. Parallel acquisition of PN sequences in DS/SS systems [J]. IEEE Transactions on Communications, 1994, 42(5): 2155-2164.

[7] 曹硕. 卫星导航信号捕获算法的研究和实现 [D]. 太原: 中北大学, 2014.

[8] 卢迪, 骆相吉, 许成舜. 混频前端抽取的串行捕获算法研究 [J]. 哈尔滨理工大学学报, 2015, 20(4): 82-87.

[9] 王伟, 徐定杰. 基于FFT的伪码快速捕获 [J]. 哈尔滨工程大学学报, 2003, 24(6): 646-650.

[10] ZHU Lufeng, ZHANG Chunxi, MA Zhiqiang. Fast fine acquistion algorithm of GPS receiver aided by INS information [J]. Journal of Systems Engineering and Electronics, 2011, 22(2): 300-305.