基于Stewart平台的导弹舱段自动对接方法研究
2017-05-03温晶晶刘承骛李贵珠
温晶晶, 刘承骛, 吴 斌, 李贵珠
(1 西北工业大学航天学院, 西安 710072; 2 西北工业集团有限公司, 西安 710043)
0 引言
导弹产品基本都是分段制造,再进行整体装配的。这些分段制造的部段一般被称为“舱段”。影响舱段装配质量的因素很多,但实践证明,对于最终装配质量的提高,改善装配技术比提高制造精度更行之有效[1]。因此,探究高精度、自动化的舱段对接技术具有重要意义。
目前我国的导弹舱段对接技术依然停留在依靠操作人员经验的阶段[2]。近年来,国内诸多总装厂也引入了先进的测量定位装置,如室内GPS系统、激光跟踪仪等,但因为缺少数字化的自动对接系统,装配效率和质量提高并不明显。郭志敏等人[3]研制了一种精密三坐标POGO柱来完成舱段对接,该装置姿态调整范围大、精度高,但成本较高,控制系统和结构很复杂;杜兆才等人[4]设计了多台三坐标直角机器人协调对接系统,该系统承载能力大、适应性强,但控制难度大,精度也不如并联机构。
文中采用Stewart平台作为自动对接系统中的调姿定位机构,充分发挥其精度高、成本适中的特性,再结合激光跟踪定位技术,设计了一套导弹舱段水平自动对接方案;系统介绍了对接方案各分系统及对接流程;细化了对接过程中的若干关键技术,主要有:求解坐标转换矩阵的直接法和模式搜索算法的对比,测量坐标系到静坐标系的转换矩阵求解方法,特征点选取位置原则和数量原则的确定,防止舱段干涉的措施,初始位姿标定方法的对比;对自动对接过程进行了误差分析,并利用计算误差构造自动对接能否完成的判别公式,再结合Stewart平台的速度公式建立了舱段位姿误差的补偿方法。
1 舱段自动对接系统的组成
文中设计的导弹舱段自动对接系统包括:车架,测量定位系统,调姿机构,控制系统。
1.1 车架
如图1所示,一次对接发生在两个舱段之间,放置在Stewart平台上的舱段称为活动舱段,放置在车架上的舱段称为固定舱段。车架下面设计有车轮,方便将固定舱段移动到合适区域。当固定舱段到达合适区域后,用千斤顶将固定舱段抬起并固定。
1.2 测量定位系统
目前,舱段对接测量定位方法主要有室内GPS和激光跟踪仪测量法。室内GPS系统在小范围(13 m以内)测量时精度不如激光跟踪仪,并且只能在固定车间内测量[1]。激光跟踪仪相对更适用于导弹等中小型舱段的局部对接过程,并且测量精度高、移动方便,重复测量精度可达5 μm/m。但激光跟踪仪在测量过程中一旦出现断光或移站,必须重新标定。
1.3 调姿机构
Stewart平台作为典型的并联机构,能够实现空间6个自由度的运动,并且承载能力强、精度高(无累积误差)[5],非常适用于大载荷、高精度、小工作空间的调姿运动[6]。综合考虑Stewart平台的特性,采用Stewart平台作为调姿机构驱动活动舱段进行空间6个自由度的运动以实现舱段自动对接。Stewart平台各驱动杆的伸缩精度是整个对接任务顺利完成的重要保证,所以必须选用高精度的丝杠导轨。
1.4 控制系统
采用IPC+PMAC运动控制卡的方式控制Stewart平台。系统组成有:工控机、运动控制卡、驱动器、伺服电机、制动器、检测单元等。运动控制卡是控制的核心;工控机负责从运动控制卡上读取并管理数据;驱动器负责驱动电机从而实现位置、速度和力矩的控制;制动器负责突发状况时即时锁死机构;检测单元负责准确检测出驱动杆长度及电机的速度和力矩信息并输出反馈信号,形成闭环回路。
Stewart平台各驱动杆本质是一个个伺服电动缸。各缸通过丝杠副将电机的旋转运动转换为推杆的直线运动,并利用伺服电机的闭环特性,实现推力、速度和位置的精密控制。如图2所示,平台运动时,上位机通过网卡给主控机发送相关运动参数指令,然后PCL841启动现场CAN进行传输,再由驱动器内部PC得到信息并驱动电机转动。电机上的检测单元检测出电机的力矩、速度、位置信息并发送给驱动器构成闭环系统以实时精确的控制各电动缸的伸缩量,最后把信息传给主控机并由主控机协调各电动缸运动以使平台达到要求的位姿。
2 舱段自动对接方案的流程
2.1 定义特征点和坐标系
如图1、图3、图4(a)所示:固定舱段对接面特征点记为H1,…,H4;活动舱段对接面特征点记为G1,…,G4;动平台特征点记为A1,…,A4;静平台特征点记为B1,…,B4。如图4(b)所示:在动平台上建立动坐标系O2-X2Y2Z2;在静平台上建立静坐标系O1-X1Y1Z1。测量坐标系记为O0-X0Y0Z0。特征点在测量坐标系下的坐标记为0H1,…,0H4,0G1,…,0G4,0A1,…,0A4,0B1,…,0B4,动平台和静平台的特征点在静坐标系下的坐标记为1A1,…,1A4,1B1,…,1B4。
2.2 对接流程
如图5所示,首先用激光跟踪仪测出所有特征点的坐标;再将特征点的坐标信息传给数据管理系统,计算出Stewart平台的初始位姿和目标位姿,并通过位姿反解算法[5](由动平台位姿反求出各驱动杆的长度)将位姿信息转化为控制信息传给控制系统;最后控制系统驱动平台到达预定位姿,如果与目标位姿还有偏差,则进行误差补偿,直至满足要求。
3 舱段自动对接部分关键技术研究
3.1 转换矩阵的求解方法
舱段自动对接过程就是从初始位姿到目标位姿的变换过程。初始位姿即活动舱段在对接前所处的位姿,目标位姿即固定舱段在对接前所处的位姿。测出各舱段特征点在静坐标系下的坐标,分别记为:1H1,…,1H4、1G1,…,1G4,则由反解方程可得:
1Hi=R1Gi+p,i=1,2,3,4
(1)
式中:p=[x,y,z]T为动坐标系原点O2到静坐标系原点O1的距离矢量;R=R(z,ψ)R(y,θ)R(x,φ)。
式(1)写成齐次坐标形式为:
(2)
显然T含有6个变量(φ,θ,ψ,x,y,z),并且可通过式(2)求解出来。下面对比分析两种求解方法。
3.1.1 直接求解法
将8个特征点的坐标向量代入式(2)得:
(3)
式(3)可简记为H=TG,显然HG-1=T。为避免直接求逆,将式(3)两边同时转置并分别取第一列得:
(4)
采用Gauss消去法解出方程组(4)中的a1,b1,c1,x项。同理可求出T中的其他项。再由θ=-arcsin(c1),φ=arctan(c2/c3),ψ=arctan(b1/a1)求出R中的具体项。于是φ,θ,ψ,x,y,z全部求出。
3.1.2 模式搜索法
模式搜索算法是一种直接寻优算法,该算法精度高且无需求导,详细原理参见文献[7]。假设T已知,先由式(3)求出活动舱段特征点坐标1H1,…,1H4的计算值,再与实测值作差求平方和构造目标函数为:
(a21xGi+b21yGi+c21zGi+y-1yHi)2+
(a31xGi+b31yGi+c31zGi+z-1zHi)2]
(5)
通过模式搜索算法求出使目标函数F值最小的φ,θ,ψ,x,y,z就是描述所求位姿变换的6个变量。
3.1.3 算例验证与对比
设平台的初始位姿和目标位姿如表1所示。初始位姿对应的固定舱段特征点坐标和目标位姿对应的活动舱段特征点坐标分别如表2、表3所示。

表1 Stewart平台的初始位姿和目标位姿
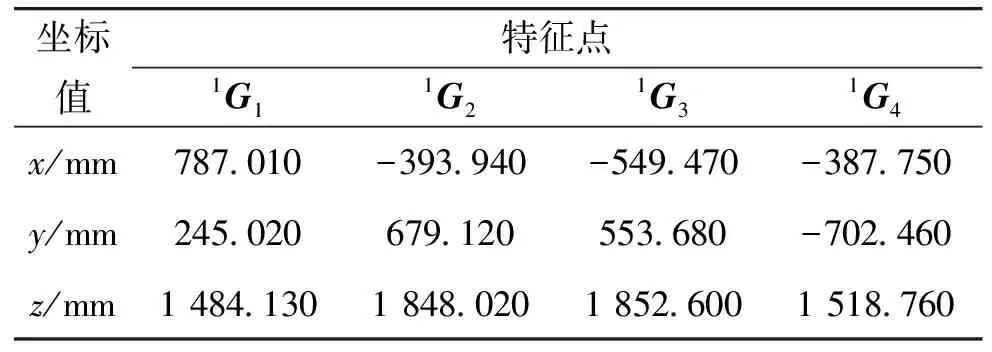
表2 固定舱段特征点坐标
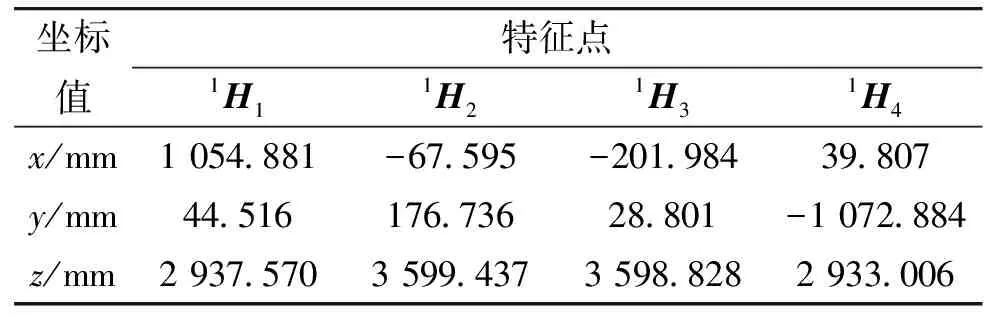
表3 活动舱段特征点坐标
结合表2、表3中的测量值分别用两种算法反推目标位姿,并和表1中的准确值比较,结果如表4所示。显然模式搜索法优于直接法。直接法计算出的位姿(特别是位置参数)误差较大,这是因为位姿中z0值相对于其他量过大,造成矩阵条件数过大而出现病态。模式搜索法可以有效避免这种情况。
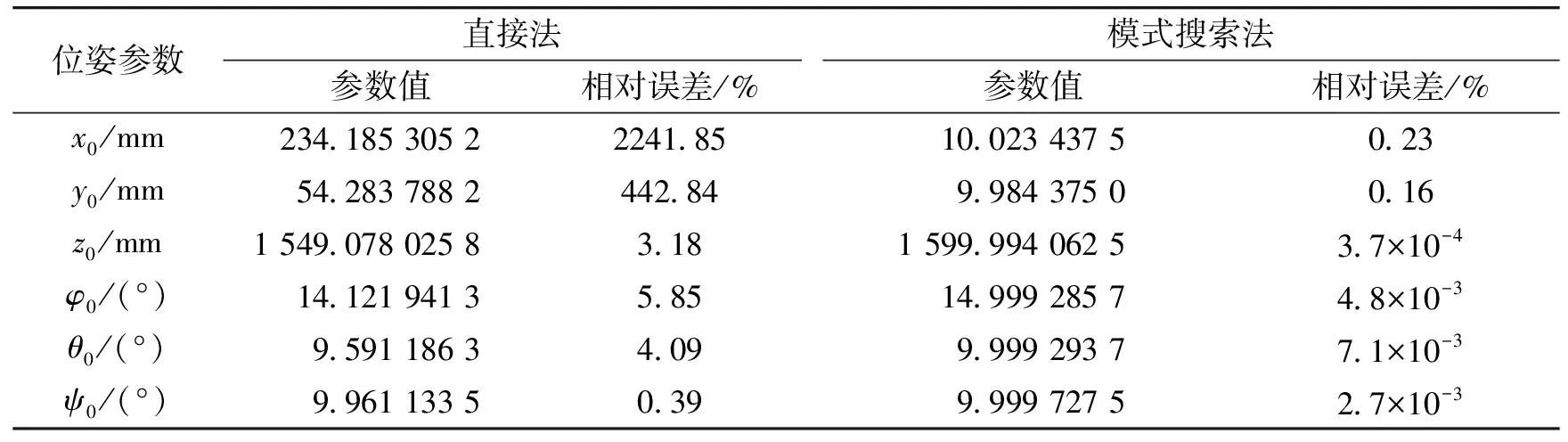
表4 两种方法计算目标位姿比较
3.2 测量坐标系和静坐标系的转换关系
活动舱段和固定舱段特征点的坐标都是相对于测量坐标系得到的,而计算目标位姿时需要将测量坐标系下的坐标值转化到静坐标系下,因此必须提前建立二者之间的转换矩阵。
设测量坐标系到静坐标系转换矩阵为1T0。先用激光跟踪仪测出静平台特征点在测量坐标系下的坐标1B1,…,1B4。再从Stewart平台三维模型中标定出静平台特征点在静坐标系下的坐标0B1,…,0B4。显然:
1Bi=1T00Bi,i=1,2,3,4
(6)
利用3.1节的方法求出1T0。设激光跟踪仪测得活动舱段和固定舱段的特征点在测量坐标系下的坐标分别为0H1,…,0H4,0G1,…,0G4。则它们在静坐标系下的坐标为1Hi=1T00Hi,1Gi=1T00Gi,i=1,2,3,4。
3.3 特征点的选取原则
位置选取原则:尽量选择容易获取且分布均匀的点,如连接舱段的销钉和销孔等。
数量选取原则:至少4对点,并且每组4个点不在同一面上。转换矩阵T共有12个变量,2对点可以列出6个方程,再加上T中部分变量满足式(7)所示的6个约束关系,理论上可以解出T中所有变量。但对接并不只是点对点重合,还要求接面的法向一致,因此两对点计算出的位姿值会出现多解性。3对点(每组3个点不能共线)也同样无法保证对接面的法向一致,还是会出现多解性。不在同一面上的4个点(其中任意3个点不能共线)可以满足要求,因为4个点中的3个确定了一个平面,剩下的一个点恰好确定了平面的法向,从而既能解出T中的变量,又保证了对接面法向的一致。当然特征点数越多,求解精度越高,但装配失误的概率也会增大。
(7)
3.4 防止舱段干涉的措施
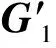
3.5 Stewart平台初始位姿的标定
计算出目标位姿后,还需知道Stewart平台的初始位姿才能根据二者差别计算出6根驱动杆的伸缩量。文中提出两种标定方法:正解标定法和激光跟踪仪测定法。
3.5.1 正解标定法
Stewart平台工作时,检测单元会反馈各杆的长度,利用正解算法[5,8](由6个驱动杆的长度求出动平台位姿)即可算出Stewart平台当前的初始位姿。该方法快速方便,但要求驱动杆长度必须测量精确,并且正解算法大多基于数值方法,误差较难控制。
3.5.2 激光跟踪仪测定法
用激光跟踪仪测量出动平台上特征点的坐标0A1,…,0A4。转换矩阵1T0的计算方法3.2节已经详细论述。则动平台上特征点在静坐标系下的坐标为:
1Ai=1T00Ai,i=1,2,3,4
(8)
同理,各特征点在初始装配位姿下的坐标也可方便标定。利用3.1节的方法可以求出Stewart平台从初始装配位姿到当前位姿的转换矩阵,而该矩阵中的φ,θ,ψ,x,y,z就是平台的初始位姿。显然,该方法精度更高,但需要反复标定特征点,操作繁琐。
3.6 误差分析与控制
3.6.1 误差分析
文中设计的舱段自动对接方案的误差主要有:测量误差、机构误差、计算误差。
因为激光跟踪仪的测量精度基本在微米级,因此测量误差可以忽略。机构误差主要包括平台的安装制造误差、机械磨损误差、机构变形误差、驱动杆伸缩误差。实际上Stewart平台作为并联机构,没有累积误差,并且平台大多采用刚度较大的金属材料制成,变形和磨损基本可以忽略。至于安装制造误差和驱动杆伸缩误差,可以通过在控制系统中增加光栅尺等高精度测量手段来弥补。

(9)

3.6.2 位姿误差补偿方法
动平台到达预定位姿后,如果还存在偏差,则需要对实际位姿进行补偿。设动平台的实际位姿广义坐标为q′=[x′,y′,z′,φ′,θ′,ψ′]T,对应各驱动杆长度为L′;动平台理论位姿广义坐标为q=[x,y,z,φ,θ,ψ]T,对应各驱动杆长度为L。设动平台广义坐标偏差为Δq=q′-q,驱动杆偏差为ΔL=L′-L。则由Stewart平台的速度方程[5]可以建立如下关系:
(10)
Lk+1=Lk+JΔqk,k=0,1,…
(11)
式中:Δqk为第k次测量的实际位姿与理论位姿坐标的偏差;Lk为第k次测量时各驱动杆的长度;Lk+1为在Lk基础上进行位姿误差补偿后各驱动杆的长度。以Lk+1为控制量驱动Stewart平台达到预定的位姿,若还存在偏差,则继续迭代,直至满足要求。
4 结论
文中基于Stewart平台设计了一套舱段自动对接方案,并介绍了各分系统及对接流程。细化了对接过程中的若干关键技术,包括:求解转换矩阵的直接法和模式搜索算法;测量坐标系到静坐标系转换矩阵的求解方法;特征点的选取原则,并论证了至少4个不在同一面上的特征点才能得到合理的结果;合理规划对接轨迹以避免舱段干涉;提出了两种Stewart平台初始位姿标定方法,分别为基于精确测量各驱动杆长度的正解标定法和基于模式搜索算法的激光跟踪仪测定法;对自动对接过程进行误差分析,并利用计算误差建立对接能否完成的判别公式,再结合Stewart平台的运动特性建立了位姿误差补偿算法。本方法为导弹装配提供了新的思路,为后续实际对接系统设计提供了理论支持。
完成舱段对接后还需拧紧螺栓以固定对接面,而拧紧过程中活动舱段也会产生微小的位姿变化,此时该如何控制Stewart平台,这方面还有待探究。
参考文献:
[1] 周丽华. 大型运载火箭自动对接技术研究 [D]. 哈尔滨: 哈尔滨工业大学自动化测试与控制研究所, 2011.
[2] 熊涛. 卫星自动对接技术研究 [J]. 航空制造技术, 2011(22): 36-39.
[3] 郭志敏, 蒋君侠, 柯映林. 基于POGO柱三点支撑的飞机大部件调姿方法 [J]. 航空学报, 2009, 30(7): 1319-1324.
[4] 杜兆才, 邹方. 多机器人协调操作系统实现飞机大型部件对接的轨迹规划 [J]. 航空制造技术, 2009(24): 88-91.
[5] 马建明. 飞行模拟器液压Stewart平台奇异位形分析及其解决方法研究 [D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2010.
[6] 易旺民, 段碧文, 高峰, 等. 大型舱段装配中的水平对接技术 [J]. 计算机集成制造系统, 2015, 21(9): 2354-2360.
[7] 张春富, 张军, 唐彦文, 等. 一种基于模式搜索的大尺寸测量移站坐标转换方法 [J]. 航空计测技术, 2003, 23(26): 12-14.
[8] 张兆印. 6-DOF并联机器人位置正解的实用解法 [J]. 计算机工程与应用, 2009, 45(9): 47-48.
