云模型在小区域GNSS高程拟合中的应用

宋利杰，李孟倩

(华北理工大学 矿业工程学院，河北 唐山 063210)

云模型在小区域GNSS高程拟合中的应用

宋利杰，李孟倩

(华北理工大学 矿业工程学院，河北 唐山 063210)

云模型；GNSS；高程异常值；高程拟合

针对远离水准点的小区域GNSS高程拟合问题，提出一种基于云模型的方法应用于小区域GNSS高程拟合。本文对远离水准点的区域内进行GPS静态测量，采用四等水准测量的方法测量区域各点的高程，采用二次多项式曲面内插得到高程异常值，由于数据较少，结果受样本数据影响大，内插得到高程异常值精度较低。运用云模型的方法将内插得到高程异常值进行处理，得到该区域的高程异常值。结果表明运用云模型处理高程异常值能有效地剔除粗差的影响，得到精度更高的高程异常值。

区域GNSS水准测量在工程测量中得到越来越广泛的应用，目前，根据测量精度的要求和测区的特性，采用的GNSS高程拟合方法并不相同，在小区域面状测量中多采用曲面拟合和多项式拟合，在条形带状工程中则可选用曲线拟合函数[1-3]，这几种方法都是在得到点坐标与高程异常值的情况下，内插或者外推得到未知点的高程异常值[4]。但是，在小区域数据较少的情况下得到的拟合函数受每个点的数据影响较大，仅采用曲面拟合或多项式拟合得到的数据拟合精度较低，因此，该项目运用云模型的方法对小区域内拟合得到的高程异常数据进行云处理，针对少量已知数据情况下高程异常值的求取，得到该区域最优的高程异常值。

小区域CNSS高程拟合是在小区域范围内少量几个点首先进行GPS静态测量，得到大地高，采用四等水准测量的方法测出各点的正常高，利用公式ζ高程异常=H大地高-h正常高求出各点高程异常值，根据点坐标(x,y)和高程异常值进行二次多项式曲面拟合得到拟合公式，根据公式可以内插得到未进行四等水准测量点的高程异常值，从而求取该点正常高。由于小区域内样本点较少，拟合得到的结果受样本数据影响较大，因此，提出基于云模型的方法用于对拟合数据定性定量的分析，使高程异常值更为准确，精度更高。

1 云模型的原理

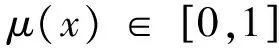
云模型用3个数据来表示其特征：

(1)期望Ex(expectedvalue)：最能代表定性概念的点，是论域内云滴的分布期望。

(2)熵En(entropy)：反映云滴的离散程度，是不确定性的度量，由云滴数据本身的离散程度和模糊程度决定。同时，又能产生云滴可能出现的范围，对云滴进行定性[8]。

(3)超熵He(hyperentropy)：用来度量熵的不确定性,能够间接反映了云的厚度，数量大云比较厚，数量小云比较薄。

正向云发生器和逆向云发生器是云的2种发生器(MembershipCloudsGenerator)，用来生成数量足够多的云滴和计算云滴的云数字特征(Ex，En，He)，正向云发生器的触发机制[5]：

(1)根据数据本身数字特征生成En为期望，以He2为方差的正态随机数En′。

(2)计算期望值Ex，以En′2为方差的正态随机数x，x就是论域空间U的一个云滴。

(4)重复(1)、(2)、(3)步骤直至生成规定的能够反映特征值的云滴。

逆向云发生器是用来计算云滴的数字特征(Ex，En，He)的，假设样本x的容量为n，其触发机制：

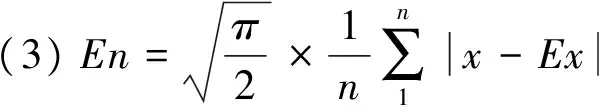
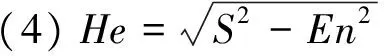
2 二次多项式曲面拟合

二次多项式曲面拟合是多项式曲面拟合中只取到二次，假设测站点高程异常值ζ，平面坐标(x,y),二次多项式曲面高程异常值拟合模型为：

ζ=x,y+ε

f(x,y)=a0+a1x+a2y+a3xy+a4x2+a5y2

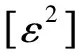
3 小区域高程异常值拟合

在山东某地约20km2范围内做静态GNSS测量，获取10个控制点的平面坐标XY及其大地高Z。采用四等水准测量的方法从已知高程点联测到各个静态点，得到各种静态点高程H，根据大地高和正常高求取高程异常值，如表1所示：

表1 各点高程异常值

将1号到9号点作为样本点，10号点为实验数据，选用二次多项式曲面拟合进行高程拟合，得到拟合函数，可根据拟合函数内插得到该范围内任意一点的高程异常值。10号点(3 940 367.803, 39 487 190.269 )，为范围内一点，高程异常值为0.241 m，将10号点的坐标带入拟合的二次多项式中求取拟合高程异常为：0.231 m，高程异常差值为10 mm。

将表1中的前9个点中任意选取其中8个数据，例如选取1～8,2～9等分组进行二次曲面拟合，得到9个拟合函数，分别将10号点带入得到不同的9个高程异常值，如表2所示：

表2 内插得到的高程异常值数据统计表

从表2中可以看出，拟合选用不同的8个数据内插得到的高程异常值差别较大，说明在样本数量较少的情况下，单个样本数据质量对整体影响较大，且第4组数据比9个数据全部进行拟合更接近真实值，说明在数量较少的情况下，并不是将所有样本数据进行拟合得到的精度更高，并且对于测区内不同的点，并不能确定选择哪组样本数据拟合效果更好。

4 云模型优化处理

由前文分析可知，对于小区域内特定一点，由于已知数量较少，选取不同的拟合数据对结果影响较大，假若有数量足够多个点用于拟合，得到的高程异常值就越接近于真实值，对表2中内插得到的程异常值进行云模型的处理，如图1所示。

图1 云模型处理10号点高程异常值

如图1所示，横轴为高程异常值，纵轴为确定度，图中的点是根据表2中高程异常值数据特征产生的500个随机点，横轴最大值和最小值是根据表2中的数字特征随机产生，最大值和最小值出现为小概率事件[8]。对图1的解释为：由表2中的拟合高程异常值进行500次随机试验推算，10号点可能出现的高程异常值范围为0.180～0.285 m，高程异常值0.23 8 m所对应的确定度最大，出现的概率更高，与实际值0.241 m最为接近。在图中0.23 m所对应的确定度为0.8，而0.21 m所对应的确定度为0.4，这并不是说0.23 m要比0.21 m精确2倍，只能说0.23 m出现的概率比0.21 m更大[9]。经比较可以看出，经过云模型处理的高程异常值要比二次多项式曲面拟合更精确。

在测区内取一点Z(3 941 253.356,39 486 822.428 )只进行了GPS测量而并没有进行四等水准测量，高程异常值根据测区内实测点进行内插计算，10个实测之中，任意取9个数据分组，每组数据不重复，共10组，进行二次多项式曲面拟合，处理数据如表3所示。根据前文分析，10组数据拟合得到的高程异常值存在较大差异，因此，使用云模型对高程对9组高程异常值进行处理，处理结果如图2所示 。

表3 Z点高程异常值拟合数据

图2所示为Z点高程异常值云模型。

图2 Z点高程异常值云模型

由图2可知，Z点高程值可能出现的范围为0.241 m到0.307 m，确定度最高所对应点的高程异常值为0.273 m，由前文分析可知，认为Z点的高程异常值为0.273 m的可信度更高。

5 结论

在小区域范围内，已知点的数量较少，在选用少量已知点数据进行GNSS高程拟合时，每个数据对拟合结果影响较大，因此，仅仅依靠函数拟合进行高程拟合效果并不理想，将云模型的方法应用于小区域GNSS拟合数据进行处理，实验结果表明，经过云模型处理的高程异常值更为精确、可信。

[1] 焦殿阳,张旭晴.曲面拟合模型在小区域GPS高程拟合中的应用[J].测绘与空间地理信息,2012,35(3):24-26.

[2] 岳仁宾.GPS高程拟合模型及其应用[D].重庆:重庆大学，2008.

[3] 康英平.GPS水准拟合方法的比较[J].测绘工程,2010,19(6)：68-69.

[4] 卢辉,刘长星. MATLAB在GPS高程拟合中的应用[J].测绘科学,2009, 34(2)：191-193.

[5] 卓金武,李必文,魏永生,等.MATLAB在数学建模中的应用 (第2版)[M].北京:北京航空航天大学出版社,2014.

[6] 陈贵林.一种定性定量信息转换的不确定性模型-云模型[J].计算机应用研究,2010,27(6):2 007-2 010.

[7] 王寅杰.云模型理论研究及其在彩色图像聚类分析中的应用[D].兰州:兰州交通大学,2013.

[8] 付斌,李道国,王幕快.云模型研究的回顾与展望[J].计算机应用研究, 2011,28(2):420-426.

[9] 叶琼,李绍稳,张友华,等.云模型及应用综述[J].计算机工程与设计,2011,32(12):4 198-4 201.

Application of Cloud Model in GNSS Height Fitting in Small Area

SONG Li-jie, LI Meng-qian

(College of Mining Engineering, North China University of Science and Technology, Tangshan Hebei 063210, China)

cloud model; GNSS; height anomaly; height fitting

A new method was proposed for GNSS height fitting in small area, which was based on the cloud model. GPS static measurement to the point in the area was carried out , and the elevation of each point in the area was measured by using the method of four level measurement. and the height anomaly value was obtained by using the interpolation of two degree polynomial surfaces. Because the data are less, the result is influenced by the sample data, and the accuracy of the interpolation is low. By using the method of cloud model, the interpolation was processed to get the height anomaly value of the area. The results show that the influence of the gross error can be effectively eliminated by using the cloud model, and the higher accuracy of height can be obtained.

2095-2716(2017)02-0006-04

2016-11-15

2017-03-29

P228

A