SVM、BP神经网络、线性回归的比较研究

韩阳，吕由，潘宇航，周齐，杨爱民

(华北理工大学 理学院，河北 唐山 063210)

SVM、BP神经网络、线性回归的比较研究

韩阳，吕由，潘宇航，周齐，杨爱民

(华北理工大学 理学院，河北 唐山 063210)

支持向量机；BP神经网络；线性回归；回归预测

支持向量机算法是一种在数据挖掘领域中运用最优化理论的监督式学习方法，在预测方面具有很强的实用性，将支持向量机算法与线性回归、BP神经网络2种算法相比较，分别设计了3种算法的求解步骤。以球团矿生产中的数据为样本，运行相应算法的软件程序对数据进行回归预测。预测结果显示：3种算法中支持向量机的预测结果最为准确，进而得出了支持向量机在数据回归预测方面具有更强的实用性，有较高的推广应用价值。

预测问题是现实生产生活中经常遇到的问题，其目的在于寻求自然事物在不同条件下相互作用的发展规律，揭示事物发展方向和趋势。在现实生产中，通常针对历史数据进行分析，挖掘历史数据包含的信息，为下一步的生产提供指导。

球团矿生产中的数据预测就是一个典型例子，即已知生产原料中硅、镁等各元素含量和温度、碱度的生产环境值，预测球团生产数据[1]。目前解决预测问题的方法有许多，总结起来可以归为2类，一是经典传统统计理论，如线性回归[2]；二是新型智能算法，如神经网络、支持向量机等[3-4]。传统的统计理论线性回归模型操作方便，它可以求出预测函数[5]，并且还可以对求出的结果进行残差检验，验证模型的精度[6]，回归方程的假设严格，需要知道引起变量改变的所有因素、随机扰动项等[7]，所以在某些情况下的适用受到限制。BP神经网络实现了从输入到输出的映射功能[8]，适合于求解内部机制复杂的问题，具有自学习和自适应能力[9]；同时，它也有一些缺点和不足，首先是它的收敛速度较慢，再者是网格训练失败的可能性较大[10]。支持向量机的特点是适用于解决小数量样本数据，可以解决高维问题，是一种有较完善理论基础的小样本学习方法[11-12]。上述3种方法都是求解预测问题较为适用的方法。

该项研究通过1个实例，分别用以上3种方法对小样本数据进行预测，分析比较这3种方法用于预测时的精准度。

1 理论基础

1.1 支持向量机

支持向量机是数据挖掘中的一项新技术，是借助最优化方法来解决机器学习问题的新工具[13]。支持向量机回归有线性回归和非线性回归[14]，对于线性回归，考虑用线性回归函数

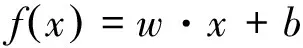
(1)

估计数据

(2)

假定存在f函数在ε精度能够估计所有的数据，那么寻找最小ω的问题可以表示为凸优化问题

min1/2‖ω‖2

(3)

约束条件

(4)

为了处理f函数在ε精度不能够估计所有的数据，引入松弛变量ξi,ξi*，因而上式可写为

(5)

约束条件变为

(6)

引入拉格朗日函数和对偶变量

(7)

(8)

其中ηi,ξi*αi,αi*大于或等于0，C>0。根据条件

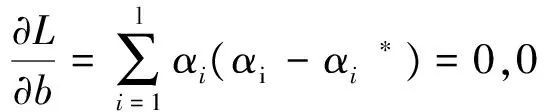
(9)

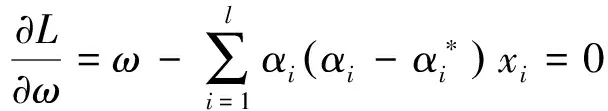
(10)

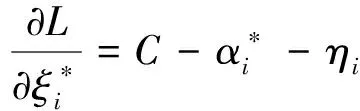
(11)

(12)

将在(14)式约束条件下，最大化(17)式求得的参数αiαi*代式入(15)式，并由(6)得回归函数

(13)

1.2 线性回归与神经网络

多元线性回归分析的模型为

(14)

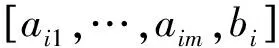
(15)

式(14)表示为

(16)

式中：En为n阶单位矩阵。

参数估计：应用最小二乘法对参数求解，结果为

(17)

BP神经网络是一种具有3层或更多层的神经网络，每一层都由若干个神经元组成。BP学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hiddenlayer)和输出层(outputlayer)，输入层各神经元负责接收来自外界的输入信息，并传递给隐层各神经元；隐层是内部信息处理层，负责信息变换，最后一个隐层传递到输出层各神经元的信息，经进一步处理后，完成一次学习的正向传播处理过程，由输出层向外界输出结果。当输出与期望不符时，进入误差的反向传播阶段。误差通过输出层，按误差梯度下降的方式修正各层权值，向隐层、输入层逐层反传。周而复始的信息正向传播和误差反向传播过程，是各层权值不断调整的过程，也是神经网络学习训练的过程，此过程一直进行到输出误差到达规定值，或者达到预设定的学习次数为止[15]。其拓扑结构如图1所示。

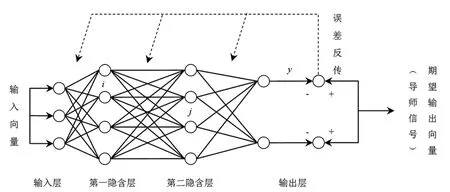
图1 BP神经网络模型拓扑结构

2 算法设计

算法设计流程，如图2所示：

图2中，各算法步骤表示的含义如下，

线性回归：

STEP1.剔除数据异常值，对可用数据做归一标准化处理。

STEP2.根据模型自变量个数和数据特点设定回归方程模型。

STEP3.对未知参量做最小二乘估计。

STEP4.对回归结果做可决系数、F检验、t检验等统计学检验。

BP神经网络：

STEP1.初始化网络、学习参数，设置网络初始权矩阵、学习因子。

STEP2.提供训练模式训练网格直到满足要求。

STEP3.将数据输入已有训练模式，计算网络的输出模式，与期望模式进行比较，若有误差则进行下一步骤，否则返回STEP2.

STEP4.计算同一层单元的误差，修正全值和阈值，返回STEP2.

SVM支持向量机：

STEP2.采用二次规划优化的算法，如内点法，即可实现支持向量机算法

约束条件变为x·(1,1,…-1-1)=0,αi,αi*≥0.i=1,…,l

STEP4.再次采用如内点法在内的二次规划优化算法，可实现支持向量机的回归。

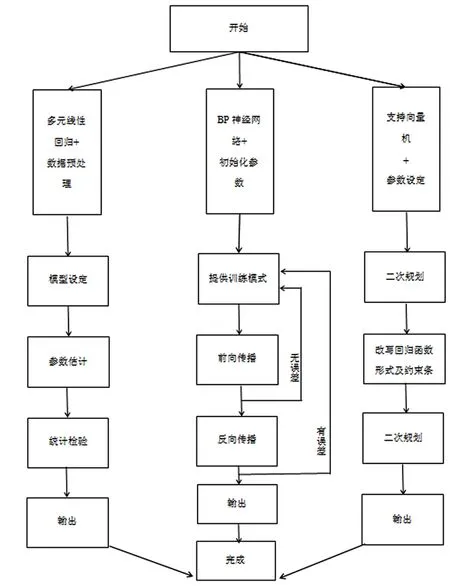
图2 算法设计流程图

3 算法实证

该项目以实际生产中的球团矿爆裂问题为研究对象。收集的原始数据输入为球团生产的各种生产条件，如硅、镁的含量、碱度、温度等，输出为球团爆裂值。数据均经过归一化处理，实验数据如表1所示。

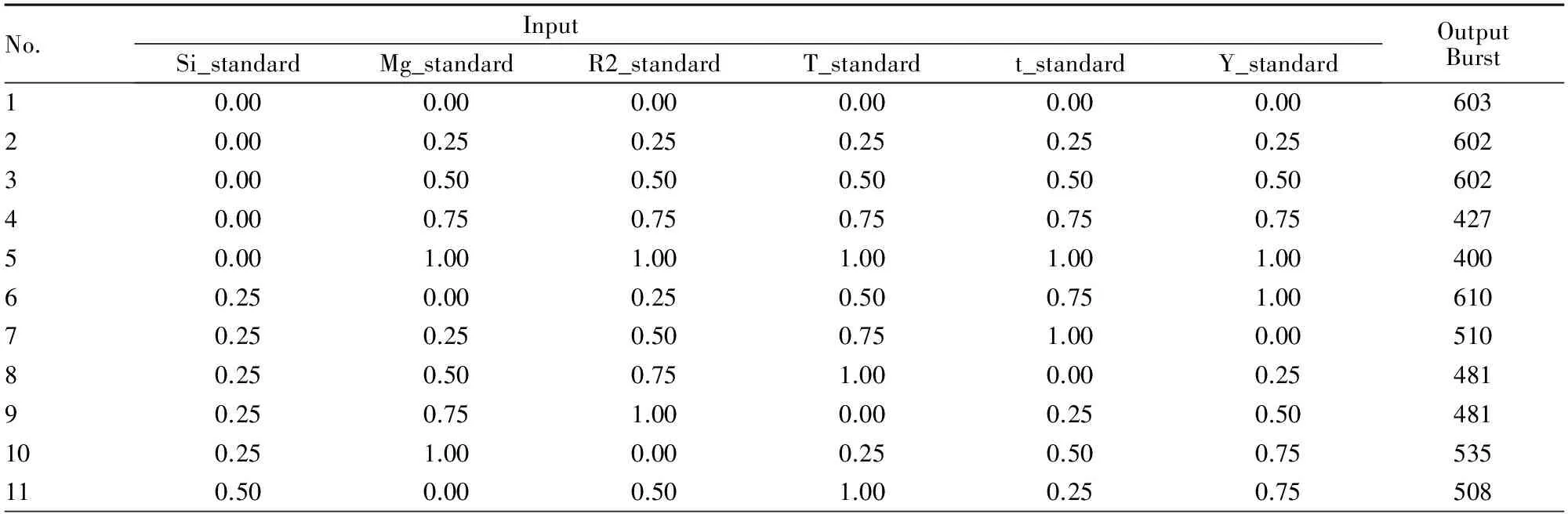
表1 原始数据

表1续

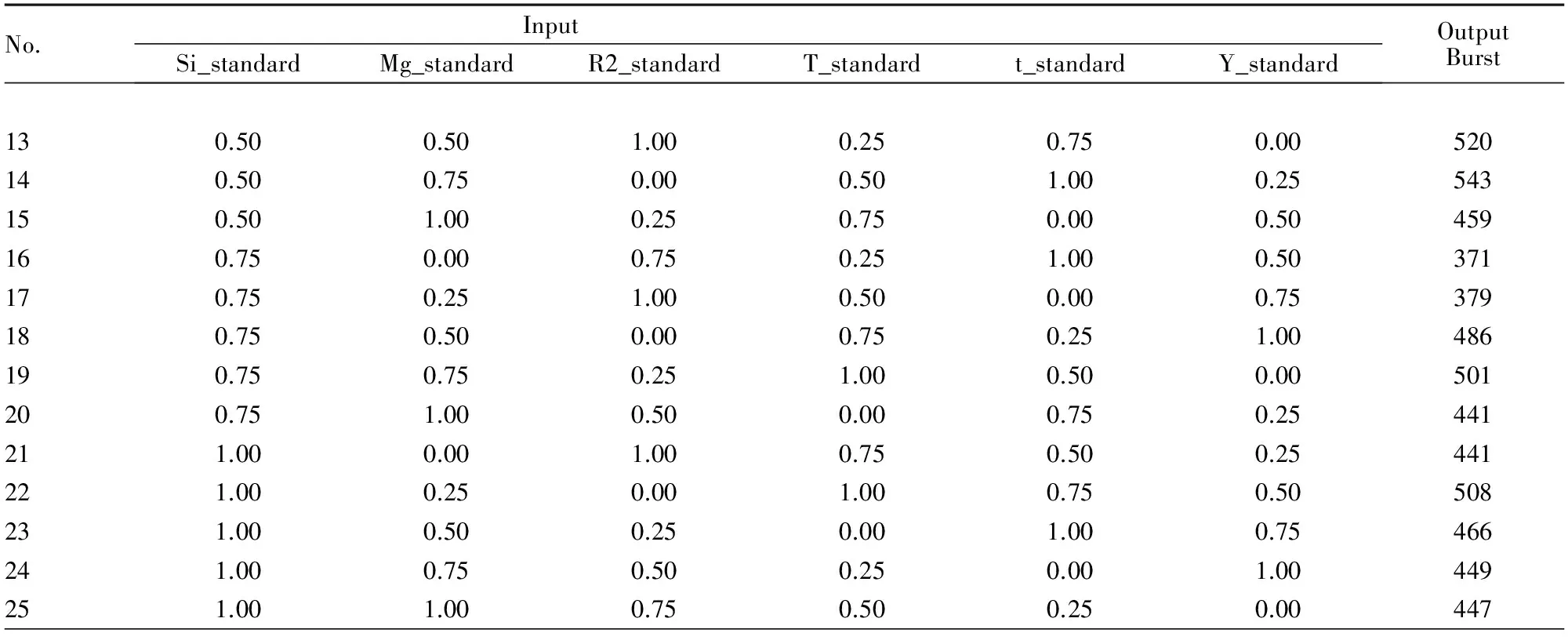
No． InputSi＿standardMg＿standardR2＿standardT＿standardt＿standardY＿standardOutputBurst130．500．501．000．250．750．00520140．500．750．000．501．000．25543150．501．000．250．750．000．50459160．750．000．750．251．000．50371170．750．251．000．500．000．75379180．750．500．000．750．251．00486190．750．750．251．000．500．00501200．751．000．500．000．750．25441211．000．001．000．750．500．25441221．000．250．001．000．750．50508231．000．500．250．001．000．75466241．000．750．500．250．001．00449251．001．000．750．500．250．00447

以数据表中前6列数据为自变量输入，最后1列数据为输出带入回归模型中做最小二乘参数估计，得出回归方程为

Y=658.38-114.08X1-52.59X2-109.75X3-37.68X4-7.21X5-25.17X6

(18)

运行神经网络和支持向量机相应的MATLAB程序，保存网络训练结果。各方法预测数据如下所示。

表2 预测结果与期望相对误差表

表2中的误差(Err)采用的为相对误差，其计算公式见式(19)：

(19)

式(19)中xpre表示爆裂次数预测结果，xtar表示爆裂次数期望结果。

运用3种预测算法的误差分布情况，由图3可知：BP神经网络算法产生的误差最大，平均相对误差达到11.68%，造成这种现象的原因是训练样本少，测试样本中输入与输出间的关系未被全部学习；多元线性回归模型产生的误差次之，平均相对误差达到7.36%，造成这种现象的原因是样本输入与输出间存在的关系并不是单纯的线性关系，通过输入指标变量的线性组合无法科学的揭示输入与输出的依赖关系；支持向量机算法产生的误差最小，平均相对误差仅为3.15%，是一种适用于探索小样本数据非线性关系的预测算法。

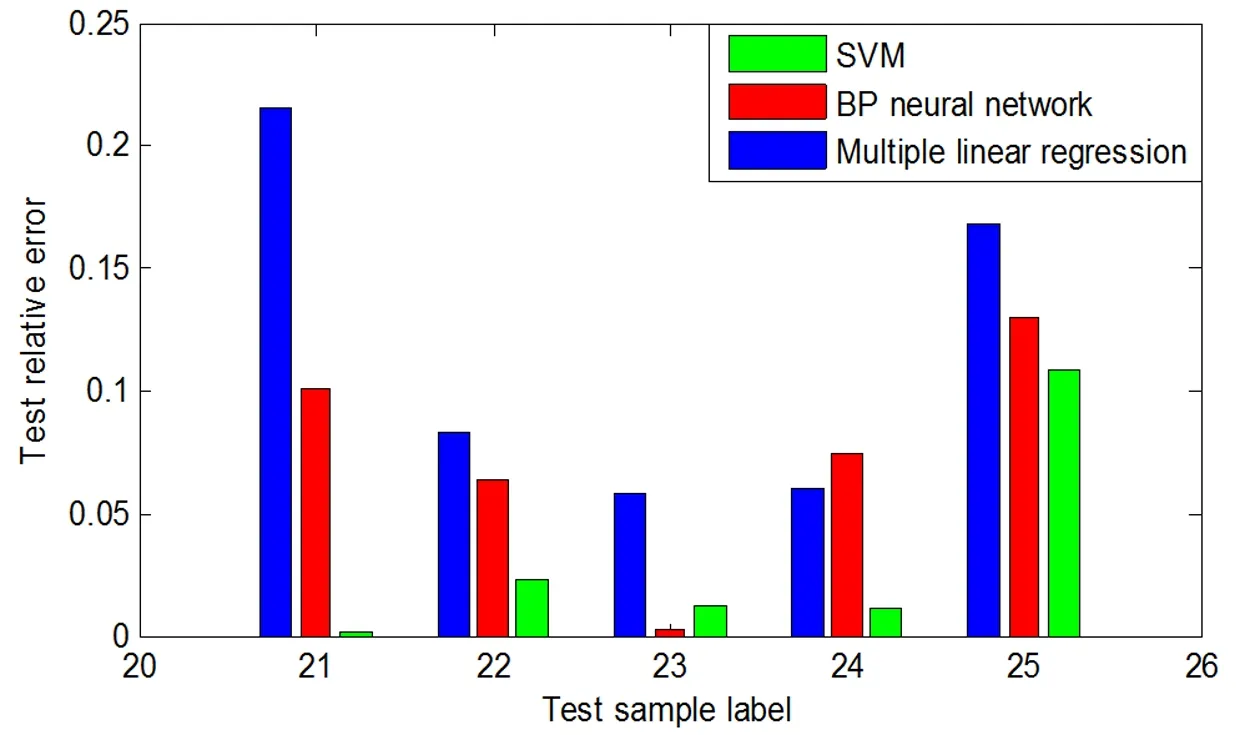
图3 3种方法预测相对误差图

4 结论

球团爆裂次数是评价球团质量的关键指标，该指标受到原料参数等因素的影响。构建爆裂次数与原料参数之间的机理模型极其复杂，并且存在大量的不确定因素，而应用统计学方法或智能算法进行预测可以有效的减轻工作量。通过BP神经网络算法、多元线性回归模型和支持向量机算法，3种方法的预测效果比较来看，支持向量机算法在预测精度方面最优，该算法值得在各领域的应用中推广。

[1] 闫洪伟. 基于数据的球团矿质量预测模型研究及其应用[D].沈阳：东北大学,2010.

[2] 王惠文,孟洁. 多元线性回归的预测建模方法[J]. 北京航空航天大学学报,2007,04:500-504.

[3] 彭望蜀. 基于BP神经网络与支持向量机的股票指数预测模型比较[J].南方金融,2013,01:71-72+91.

[4] 于国强, 张茂省, 王根龙, 等. 支持向量机和 BP 神经网络在泥石流平均流速预测模型中的比较与应用[J].水利学报, 2012 (s2): 105-110.

[5] 李珺. 基于因子分析的多元线性回归方法及其在股价预测中的应用[D].南京：南京大学,2014.

[6] 张晓瑞,方创琳,王振波,等. 基于RBF神经网络的城市建成区面积预测研究——兼与BP神经网络和线性回归对比分析[J].长江流域 资源与环境,2013,22,(06):691-697.

[7] 任丹. 基于多元线性回归模型的电影票房预测系统设计与实现[D].广州：中山大学,2015.

[8] 黄丽. BP神经网络算法改进及应用研究[D].重庆:重庆师范大学,2008.

[9] 李佟, 李军. 基于BP神经网络与马尔可夫链的污水处理厂脱氮效果模拟预测[J]. 环境科学学报, 2016, 36(2):576-581.

[10] 王德明, 王莉, 张广明. 基于遗传BP神经网络的短期风速预测模型[J].浙江大学学报(工学版), 2012(5):837-841.

[11] 杨锡运, 孙宝君, 张新房,等. 基于相似数据的支持向量机短期风速预测仿真研究[J]. 中国电机工程学报, 2012, 32(4):35-41.

[12] 鲍漪澜. 基于支持向量机的金融时间序列分析预测算法研究[D].大连：大连海事大学,2013.

[13] 张华, 曾杰. 基于支持向量机的风速预测模型研究[J].太阳能学报, 2010, 31(7):928-932.

[14] 宋云雪, 张科星, 史永胜. 基于多元线性回归的发动机性能参数预测[J].航空动力学报, 2009, 24(2):427-431.

[15] 徐黎明, 王清, 陈剑平,等.基于BP神经网络的泥石流平均流速预测[J].吉林大学学报, 2013, 43(1):186-191.

Comparison of SVM, BP Neural Network and Linear Regression

HAN Yang,LV You, PAN Yu-hang, ZHOU Qi, YANG Ai-min

(College of Science,North China University of Science and Technology,Tangshan Hebei063210, China)

SVM; BP neural network; linear regression;regression forecasting

Support vector machine algorithm is a kind of supervised learning method which uses the optimization theory in the field of data mining, and has strong practicability in forecasting,compare SVM with linear regression and BP neural network,then the algorithm of three algorithms is designed respectively.Use the data of the pellet production as sample,the software program running the corresponding algorithm predicts the data.The prediction results show that the support vector machine is the most accurate in the three algorithms,then obtained that the support vector machine in the data regression prediction has a stronger practicality, a higher value to promote the application.

2095-2716(2017)02-0104-05

2016-11-24

2017-04-01

国家自然科学基金项目(51674121)；河北省硕士研究生创新资助项目(CXZZSS2017071)。

TP301.6

A