数形结合法在我们数学学习中的妙用

祝铭

摘要：对于我们高中生而言，高中时期的数学课堂学习较为枯燥，经常处于一种被动的学习状态之中，我们觉得累，老师也觉得累。在数学学习中如果引入数形结合的学习方法可以有效的改变这种疲劳的学习状态，“数形结合”是一种很重要的数学思想，在我们学习过程中如果能够好好的加以体会和利用，往往会给我们解题带来很大帮助。

关键词：数形结合；数学；学习；妙用

高中数学一直以来就是重头戏，作为我们高中生在答题时要细心，遇到难题要耐心。审——审清题意；读——读懂材料；抓——抓住关键词语；获——获取有效信息；答——给出正确答案。数形结合思想的深入很重要，它是一种非常有效的思维模式，它通过将比较抽象难懂的数学知识或题目，转变为形象生动的的图形，以便来帮助我们学生快速而精准地理解数学知识。

一、 数形结合的作用

从初中学习到高中学习，数形结合法的思想一直被我们使用着，它是一种贯穿于数学学习的主要解题思想方法，可以帮助我们学生有效的解决学习中所遇到的数学难题，通过用几何来对代数进行诠释，可以全面的显现出数形结合思维的重要性。自从上高中以来，我觉得数学学习更加灵活有趣，复杂抽象的问题使用数形结合法后变的条理清晰，简单明了。这让我对数学的好奇心神秘感又增强了，也间接的提高我的数学学习兴趣和自信心。以前有的时候我对数学是有抵制心理的，为什么呢？因为高中数学知识很多都很抽象，同时具有形式化与符号化等特点，学习起来较为枯燥且吃力。在我们数学老师的指引下，我将数形结合法科学合理的应用到学习中后，很多繁琐难懂的数学点用几何图形直观的画出来了，让我对问题的重点一目了然，也帮助我的发散性思维的养成。

二、学习过程中数形结合的主要应用

1、数形结合法在集合中的应用。说到集合，想必我们高中生再熟悉不过了，集合问题是我们学习数学中很基础的问题，集合知识的学习与领悟会帮助我们学生轻松的解决以后函数中的取值范围的问题。数形结合法能够轻松的帮我们解决完成集合里出现的问题，课本上列举的分为数轴解决法和文氏图法。例如：文氏图法的一个例子，一项活动分为A和B两个环节，一共有50人加入这一活动，20人加入了A环节，35人加入了B环节，问一共有多少人既加入的A环节又加入了B环节。利用数形结合法中的文氏图法，会很简单形象的进行回答，如图1所示。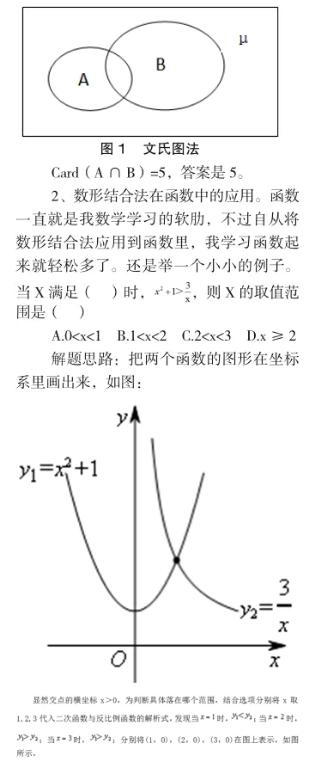

显然x的取值范围为x≥2.

本来看上去复杂的题目，通过数形结合变的清晰多了，以前做函数题目无从下手，数形结合的深入后变的清晰明了。

3、数形结合法在绝对值问题中的应用。我身边的同学，当遇见解函数绝对值的问题的时候，巧妙的运用数形结合法大大的加快解决该类题目的速度，有效的将问题简单化，数形结合法的魅力大大的显现出来了。例如：求函数y=|x-2|+|x+3|的值域。

通过下面的图的标注解释，答案一目了然。

当P点在AB线段之内时，y则等于5，当P点在AB线段以外时，函数的值域则为（5，+∞）。

三、结语

我们老师在课堂上让数形结合的教学思想大放异彩，我们学生也终身受用。自从学习数形结合法以来，以前枯燥无味的数学课变的生动有趣。我们爱学，老师爱教，一种融洽温馨的数学学习氛围在我们班级中生根发芽，开花结果。

参考文献

[1] 姚爱梅.高中数学中数形结合方法的有效应用[J].教学研究，2012，（4）：50.

[2] 申光娅.高中数学中数形结合的应用[J].教学教研，2012，（20）：61.

[3] 卢向敏.数形结合方法在高中数学中的应用.內蒙古师范大学，2013，（11）.