层次分析法在解决企业资金使用中的应用研究

温立刚

(中国石油大学胜利学院 人事处,山东 东营 257061)

层次分析法在解决企业资金使用中的应用研究

温立刚

(中国石油大学胜利学院 人事处,山东 东营 257061)

企业资金使用问题一直是企业亟需解决的难题,通过层次分析法建立企业资金分配层次的模型,通过求解,最终得出企业更倾向于将资金用于新技术设备的引进。结论进一步表明通过购买新设备进行企业升级改造在增强企业员工凝聚力、改善企业生产水平和提高员工生活水平方面能够产生更直接和更明显的效果。

企业资金;层次分析法;资金分配

企业资金的合理有效使用是企业发展的有效保障,各企业通常都会对企业资金的使用进行分析研究,以发挥企业资金的最大效用。目前关于资金使用的研究主要集中在主管层面,缺乏客观分析,而层次分析法将定性分析与定量分析相结合，对企业资金的使用分析更准确明晰,可以明确资金的投入方向,合理使用企业资金,从而促进企业发展。

一、问题分析

企业资金的使用通常有四种途径:给单位员工发放奖励;给单位员工改扩建各种福利设施;对单位员工进行业务培训;购买新设备进行企业升级改造。这四种途径在增强企业员工凝聚力、改善企业生产水平和提高员工生活水平方面都各有优势[1]。企业在资金充裕的情况下,可将一部分资金直接用于提高职工福利,但并不是所有的企业都有大量可支配的资金来提供给员工做福利。由于每个员工需求不同,有的员工需要直来直去的现金使用;有的员工看重职工宿舍、食堂等福利设施的建设;有的员工则更看重自己工作能力的提升,比如参加业务学习、培训等。而作为企业决策者则更希望引进新的技术设备和企业技术升级来直接提高企业竞争力[2]。如何更有效地分配企业资金成为企业面临的难题。

二、问题解决

针对这个问题,利用层次分析法进行分析,将问题分为三个层次,即:目标层(做出资金分配的决策),准则层(增强企业员工凝聚力、改善企业生产水平和提高员工生活水平)和方案层(给单位员工发放奖励、给单位员工改扩建各种福利设施、对单位员工进行业务培训及购买新设备进行企业升级改造)。

(一)模型假设

(1) 假设企业没有发生紧急情况,这笔资金不会被调用,这样不管是直接发放奖金还是用来修建宿舍餐厅等设施,都不会对企业的资金运转产生影响。

(2) 假设这笔资金都以供选择方案的形式用于企业的发展,即将这部分资金全部用于所做出的决策,以便达到最好的实施效果。

(3) 假设所有的员工均参与投票决策,以便于通过统计人数来确定尺度。

(二) 模型建立

企业资金使用的最终目标,就是要完成这些资金的分配以达到促进企业效益和提高员工的生活水平[3]，因此将资金分配作为目标层。要达到目标层所要期待的目标,需要以增强企业员工凝聚力、改善企业生产水平和提高员工生活水平三个方面为判断准则,以求在这三方面均达到比较理想的效果。为达到预期的准则,需要通过以下四个方案:(1)给单位员工发放奖励;(2)给单位员工改扩建各种福利设施;(3)对单位员工进行业务培训;(4)购买新设备进行企业升级改造,方案层由此确定[4]。

根据上述分析构建的资金分配层次结构示意图见图1。

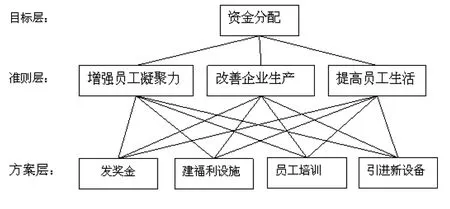
图1 资金分配层次结构示意图

(三)构造成对比较矩阵

在处理现实问题中往往需要有标度,下面给出几个典型标度的表达式(表1)来比较各个定性重要程度与对应的定量之间的相互关系。2、4、6、8 为对应上述程度的中间k值。

用到的距离比较判断表如表2所示。

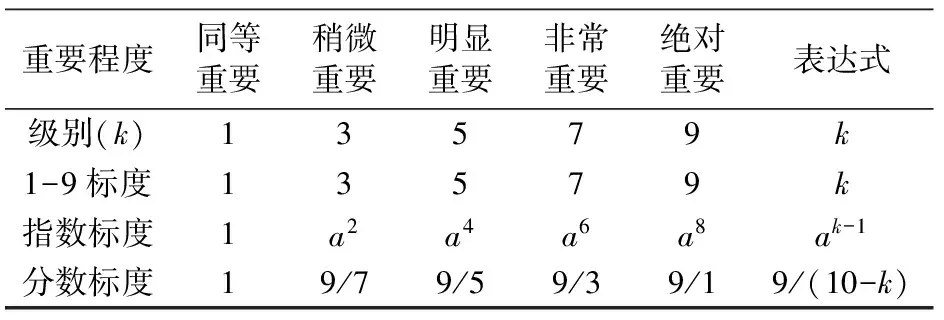
表1 几种标度表达式

表2 距离比较判断表

设在该模型中增强企业员工凝聚力、改善企业生产水平和提高员工生活水平三个准则条件分别为x1、x2、x3,并对该三个判决条件进行比较,判定他们对于资金使用决策的重要程度,在这次资金分派中我们认为最重要的就是改善企业生产水平,只有这样才能从根本上提高生产率,进而提高企业效益;其次就是提高员工生活水平,让员工有一个好的生活生产环境有益于企业招聘新员工并留住老员工;再次是增强企业员工凝聚力来提高生产效率。参考表1,得到对比矩阵(正互反矩阵):

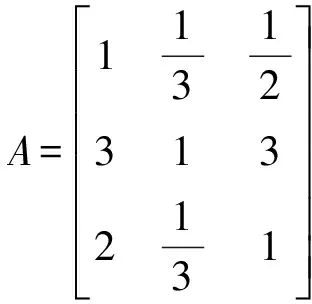
(四)模型的求解

实际上在构造成对比较矩阵时要求满足众多等式是不可能的,因此退而要求成对比较矩阵有一定的一致性,检验成对比较矩阵A一致性的步骤如下:

(1) 计算随机一致性指标

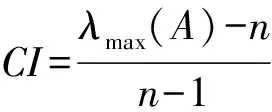
(1)

(2) 根据成对比较矩阵的阶数查看表3,得出该n阶矩阵平均随机一致性指标RI(它只与矩阵阶数n有关)。

表3 随机一致性指标RI的数值

(3) 计算成对比较矩阵的随机一致性比率

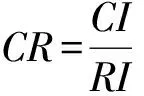
(2)

在解决这类问题的时候我们可以借助MATLAB工具来实现,因为MATLAB本身带了很多矩阵求值的函数,用MATLAB语句算出矩阵A的最大特征根为λmax=3.053 6,带入式(1)有:

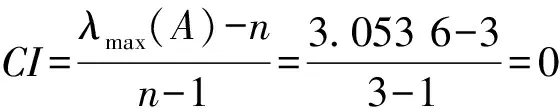
参考表3,当n=3的时候,在表中查得RI=0.58。带入式(2)有:

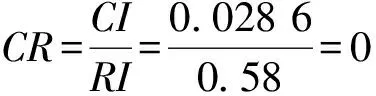
且0.046<0.1,即通过了一致性检验。计算出最大特征值λmax=3.053 6所对应的特征向量并将其标准化后有:

α=(0.157,0.594,0.249)T;

这样便完成了目标层与准则层之间的权向量的计算,用上面同样的方法构造第三层对第二层的每个标准的成对比较矩阵,不妨设他们为B1,B2,B3,其尺度标准可以通过员工投票的方式来确定,按投票比例来确定尺度标准。现在假设:

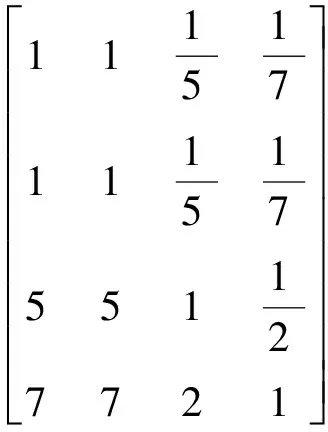
其中,B1,B2,B3分别表示四种解决方案对标准层3个因素的成对比较矩阵,例如B1表示四种方案对调动劳动者积极性方面的比较,B2中b32=3表示方案三比方案二更能提高企业技术水平,如此分别计算出B1、B2和B3的权向量(标准化的特征向量),ak最大特征值一致性指标ak和一致性比率CRk结果列在表4中(其中K=1,2,3)，CR均小于0.1,则所有的对比矩阵均通过一致性检验。

表4资金分配问题的第三层计算结果

四个方案在目标中的组合权重应该为α与αk对应向量的两两乘积之和,如方案一,即将这笔资金作为奖金发给单位员工，在目标中的组合权重应该为:

P1=0.157×0.630+0.594×0.070+0.249×0.256=0.206;

同理计算出下面方案的组合权重分别为:

P2=0.157×0.128+0.594×0.007+0.249×0.256=0.090;

P3=0.157×0.181+0.594×0.322+0.249×0.387=0.316;

P4=0.157×0.630+0.594×0.070+0.249×0.256=0.350。

分别求出权重比例,于是得到组合权重向量a(3)=(0.214,0.094,0.328,0.363)。

到这里本次层次分析法在多目标任务决策上的应用已经完成,四个方案在目标层的影响分别占到了20.6%(给单位员工发放奖励),9.4%(给单位员工改扩建各种福利设施),32.8%(对单位员工进行业务培训),36.3%(购买新设备进行企业升级改造),经过对比,方案四比重明显优于其他三个方案,所以选择方案四即用这笔资金来进行企业升级可以在增强企业员工凝聚力、改善企业生产水平和提高员工生活水平三方面得到更好的综合效果,进而提高企业效益。

三、结语

企业在日常的资金使用中也更倾向于用一部分资金来不断引进新的技术设备,因为这的确能够在增强企业员工凝聚力、改善企业生产水平和提高员工生活水平三方面产生的效果更直接而且更明显,而其他几种方案尤其是方案二给单位员工改扩建各种福利设施则回报时间比较长,这也是现实中企业并不热衷于扩大食堂宿舍方面建设的原因之一。

[1] 张丹.企业营运资金管理浅析[J].全国商情(经济理论研究),2015(24):124-126.

[2] 汤玮.关于企业营运资金管理研究[J].财经界(学术版),2016(5):78-80.

[3] 金长友,王惠明,钟建华.资金使用在企业管理中存在的问题及对策[J].科技信息,2009(7):214-216.

[4] 梁保松.模糊数学及其应用[M].北京:科学出版社,2007:115-117.

[责任编辑] 李伟娟

2017-01-25

温立刚(1977—),男,山东德州人,中国石油大学胜利学院人事处工程师,主要从事企业管理研究。

10.3969/j.issn.1673-5935.2017.01.023

F275.1

A

1673-5935(2017)01- 0082- 03