基于Excel的多元线性回归优化模型预测地表水高锰酸盐指数
2017-04-28孙晓蕾
孙晓蕾
(辽宁省鞍山水文局,辽宁鞍山114039)
基于Excel的多元线性回归优化模型预测地表水高锰酸盐指数
孙晓蕾
(辽宁省鞍山水文局,辽宁鞍山114039)
本文借助Excel软件对小姐庙监测断面的SS、BOD5、CODCr和CODMn监测数据进行线性回归全种类组合拟合,并采用校正R2法优化选择,最终形成一个三元线性回归优化模型,经统计检验可良好表达CODMn与其它三项的线性关系。将实际监测数据代入模型计算得出的CODMn数值与实际监测值之间的平均相对误差为7.35%,在可接受范围内,因此,该方程可作为辅助手段应用于实际监测工作中。
Excel;多元线性回归;优化模型;预测;高锰酸盐指数;地表水
在物理、化学实验或实际经济问题中,很多情况都要求研究自变量和因变量之间存在的关系,确定由这2个变量所决定的曲线以及最佳拟合参数。由一个或一组随机变量来预测另一个随机变量时建立的模型及所作的统计分析,统称作回归分析[1]。当只有一个自变量和一个因变量,且它们是线性关系时,称为一元线性回归;当自变量个数大于1,且因变量与自变量之间仍为线性关系时,称为多元线性回归。也就是说,多元线性回归预测是利用历史资料建立多元线性回归模型,研究某一因变量与两个或两个以上自变量之间相互关系的理论和方法。在实际生产生活中,常常是多个因素共同影响而产生相应现象,因此,由多个自变量筛选优化后建立的多元线性回归模型,比单一自变量建立的一元线性回归模型更符合实际,更能准确地预测因变量的变化,可广泛应用于各领域。
多元线性回归模型一般采用计算机编程或专业计算软件来进行数据处理与计算,处理繁琐且相关人员需要编程或软件运用能力。Microsoft Office Excel是一个普遍使用的办公软件,具有强大的数据处理与分析能力,操作界面简洁、使用方法简单、涵盖函数广泛、数据处理精确,可快捷、简便地实现多元线性回归模型的计算与分析[2]。
1 多元线性回归模型
1.1 矩阵解法原理
设因变量y和自变量x1,x2,…,xk满足以下线性关系:
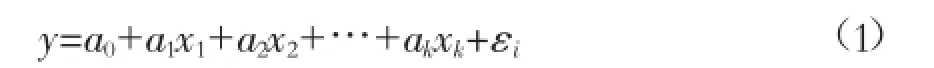
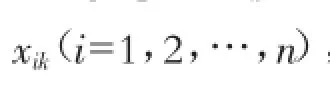

写成矩阵形式即:

其中,ε1,ε2,…,εn是n个相互独立且服从同一正态分布n(0,σ)的随机变量。残差平方和为
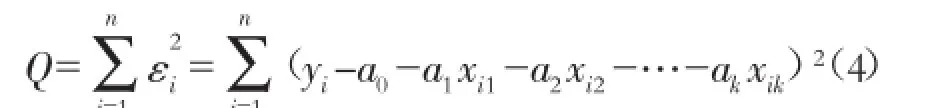
为寻找使Q最小的a0,a1,a2,…,ak,则Q分别对a0,a1,a2,…,ak求偏导数,并满足下列方程组:
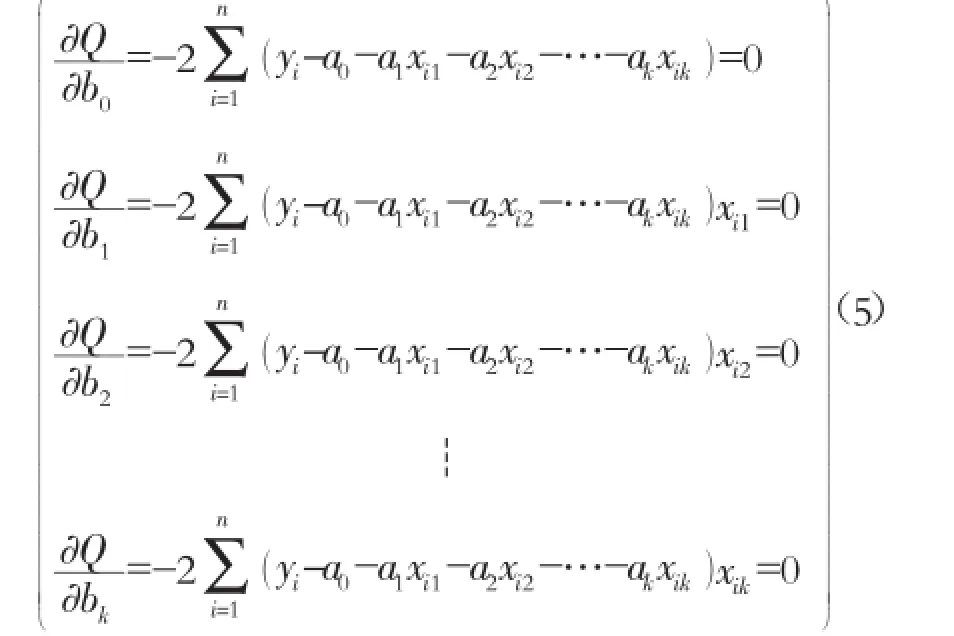
整理后用矩阵形式表示为:XT=(y-XA)=0
则回归参数最小二乘解

所得回归方程为:

1.2 最优模型选择
1.2.1 原理
1.2.2 方法选择
自变量优化选择一般采用最优子集法,即对全部自变量进行各种不同组合所建立的回归模型进行比较,从中选出一个“最优”的回归模型,则这个回归模型可良好地表达y与xi之间的关系,使其预测的结果最为准确。挑选最优回归模型的方法一般有R2法,校正R2法,Cp统计量法,AIC、BIC及AICC信息量准则等等[3]。本文采用校正R2法进行最优子集的选择。

R2是回归平方和与总平方和的比值,反应了回归方程对y的解释能力,该值越接近1,模型的拟合程度越高。但自变量个数的增加会引起残差平方和减小、R2增大,因此,尽管某些自变量与y线性关系不显著,将其引入模型后,却也会使R2增大。为了避免自变量个数对R2的影响,让R2单纯反应回归模型的拟合程度,则引入了调整判定系数R′2。

其中:k——自变量个数;n——样本个数。
一般当k∶n大于1∶5时,R2会高估实际的拟合优度,这时,宜采用R′2来说明方程的拟合优度,也就是自变量对y的解释能力。
2 应用
2.1 原始数据汇总及参数设定
鞍山市海城市牛庄镇的小姐庙监测断面,从2015年5月至2016年4月的悬浮物(SS)、生化需氧量(BOD5)、化学耗氧量(CODCr)和高锰酸盐指数(CODMn)监测数据见表1。设自变量SS为X1、BOD5为X2、CODCr为X3,因变量CODMn为Y,以X1,X2,X3与Y的变化规律分别建立线性回归模型并进行各种检验,进而选择最优的回归模型作为小姐庙监测断面的高锰酸盐指数预测模型。
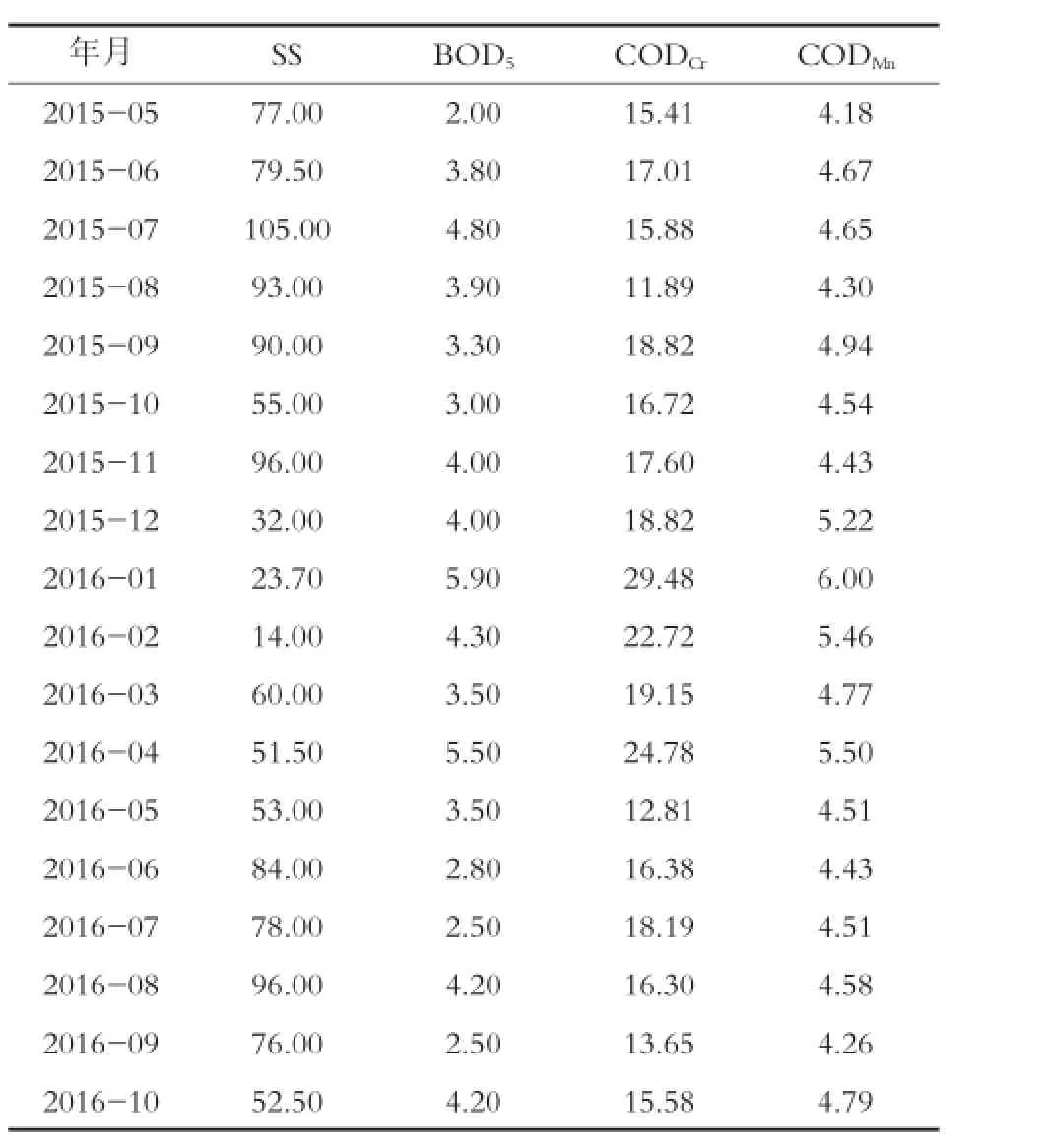
表1 小姐庙监测断面各项监测数据
2.2 各自变量与因变量之间的线性相关关系
2.2.1 线性拟合步骤
线性拟合工具采用Microsoft Office Excel 2016专业版,拟合步骤:
1)新建Excel表格,并输入原始数据(表1);
2)在“插入”中“图表”,点击“散点图(X,Y)”,选择横竖坐标数据,生成数据散点图;
3)点击选择散点图上的数据坐标点,鼠标点击右键“添加趋势线”,选择“线性”、“显示公式”、“显示R平方值”;
4)右键点击工具栏“数据”标签,选择“自定义快速选择工具栏”,点击“加载项”并“转到”,然后选择“分析数据库”后“确定”,则启动“数据”标签的“数据分析”宏模块;
5)点击“数据分析”,选择横纵坐标的数值区域X,Y,并点击选择需要计算呈现的数值,并“确定”,则在新表格中生成线性回归分析报告。
2.2.2 线性拟合
分别对X1与Y,X2与Y,X3与Y,X1、X2与Y,X1、X3与Y,X2、X3与Y,X1、X2、X3与Y进行线性拟合并生成线性回归分析报告,如图1,2所示。
2.2.3 回归模型优化选择
根据线性回归分析报告结果汇总表(表2)所示,可知调整后R2最大的为自变量选择X1,X2,X3拟合生成的线性回归模型。则根据图2可得小姐庙监测断面优化后的三元线性回归模型为:
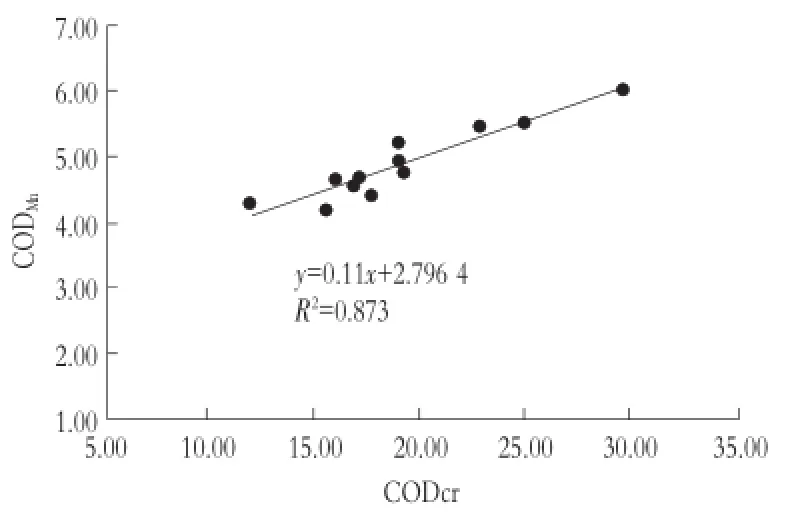
图1 X3与Y线性关系
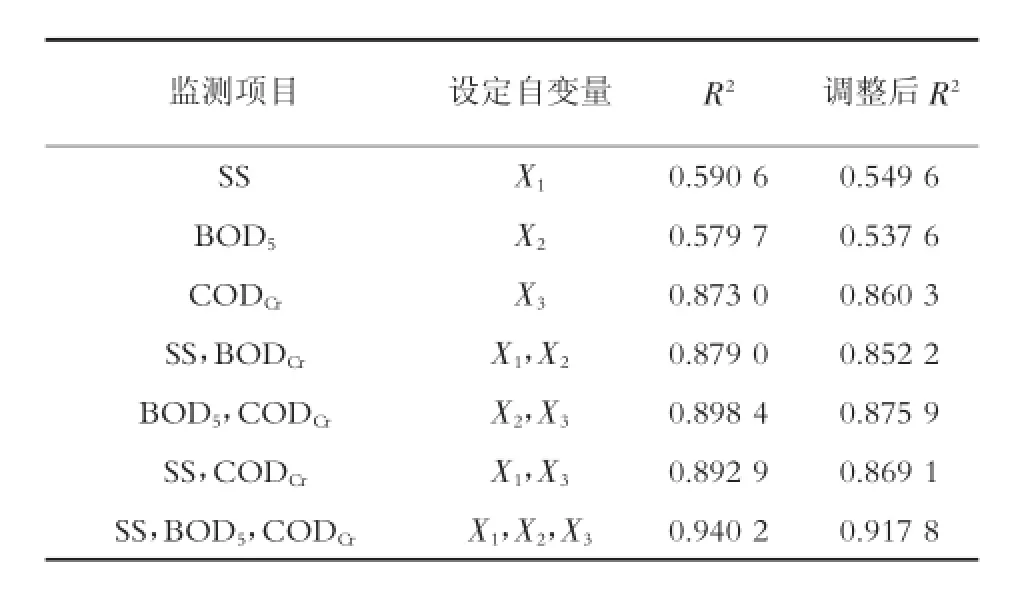
表2 线性回归分析报告结果汇总
2.2.4 三元回归模型统计检验
1)F检验
F检验是确定回归模型自变量与因变量之间是否存在显著线性关系的评定指标。根据置信度查询F分布表获得检验显著线性的临界值Fa,如果F>Fa则回归线性模型假定有效,自变量与因变量有线性关系,也就是说回归线性模型中的所有自变量足够解释因变量的变化趋势;但如果F<Fa则反之,回归线性模型显著不成立[4]。
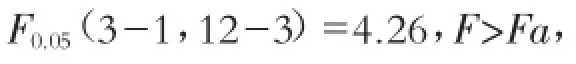

图2 X1,X2,X3与Y线性回归分析报告
2)t检验
t检验是t统计量对回归模型的每个系数进行逐一检验,通过查t分布表得到临界值ta,若t≥ta,回归系数bi有显著意义,则自变量xi应保留在回归模型内;若t<ta,应去掉自变量xi,并重新建立回归模型。
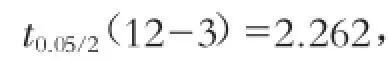
2.2.5 数值预测
将表1中2016年5月份至10月份的数据X1,X2,X3代入三元线性回归模型,预测得出Y值,并与实测值Y0计算相对误差,见表3。
3 结论
1)本文根据多元线性回归模型基本原理对小姐庙断面的SS,BOD5,CODCr和CODMn进行全种类情况线性拟合,采用校正R2法进行回归模型的优化选择,形成拟合度较高的三元线性回归方程,格管控砂石资源乱用行为,制定合理的采砂规划,逐渐恢复河底自然形态,保障了洪峰平稳过渡,还有利于恢复水沙平衡。
4)推广了水生态环境保护的理念。警示牌和围栏的设置,对沿岸影响水生态环境的生活和生产行为起到警示和警告的作用,同时也宣传了水生态环境保护的理念,将生态文明意识全社会推广。
辽宁省水生态修复已经取得了一定的成效,但距离水生态环境健康还有较大差距。因此,在今后的河道治理工作中还需要有两方面的侧重:
1)通过加强管理和维护,巩固已经取得的成果。加强河道监管体系的建设,建立健全河道管理组织机构,逐步完善各项管理制度,实施有效的管理手段,逐步实现恢复河道原貌和生态,完善河道各项许可程序,规范河道开发秩序,强化监管,严禁各种破坏河道生态环境的行为,实现河道生态的持续健康发展,强化日常管理,确保河道行洪顺畅,恢复河道生态环境,维护河流健康。
2)继续深入研究辽宁省水生态环境影响主因,完善水生态修复理论和方法研究,加强水生态修复措施实施效果。深入剖析影响辽宁省河流健康的主要因素,并以河流自然修复理论为基础,平衡河流的自然属性和社会、经济发展需求的关系,完善我省河流水生态修复理论和治理方法,力争最大限度地恢复河流的生态功能,提出科学合理的全方位多行业联动的水生态修复治理措施。
[1]朱党生,张建永,李扬,等.水生态保护与修复规划关键技术[J].水资源保护,2011,27(5):59—64.
[2]李明传.水环境生态修复国内外研究进展[J].前沿,2007(11):25—27.
X522
A
1002-0624(2017)04-0012-03
2016-05-25
