陡河水库年径流系列变异点分析

和吉，燕琴，雷冠军

（1.华北水利水电大学水利学院，河南郑州450000；2.中国水利水电科学研究院水资源研究所，北京100038）

陡河水库年径流系列变异点分析

和吉1，燕琴1，雷冠军2

（1.华北水利水电大学水利学院，河南郑州450000；2.中国水利水电科学研究院水资源研究所，北京100038）

文中利用R/S分析法和滑动平均系数法2种方法对陡河水库流域1953—1999年47年的降雨、径流序列进行了变异点分析，可知陡河水库年径流的变异点为1975年和1985年，与陡河流域70年代大兴水利工程、80年代降雨偏枯及地下水开采过量等人类活动因素对其的影响相符，结果可靠，具有一定的实用价值。

R/S分析法；滑动平均相关系数法；年径流；陡河水库

变异是指水文观测序列在某个时刻突然变化，发生变化的时刻称为变异点。传统的水文序列变异点的研究方法有水量平衡法、对比分析法、流域水文模拟法、熵值法、相关系数法等[1]。这些方法大都以单纯的数理统计变量来对系统进行分析检验，但序列值的基准点的选择受人为因素影响，使得变异点很难一致[2]。而R/S分析法与滑动相关平均系数法的共同点是不直接对水文序列的均值、方差等系统状态变量分析检验，且R/S分析法比较强健，假定条件少，能将随机序列与非随机序列区分开；滑动相关系数法研究两个相关序列之间相关的性变异，方法简单[3]。

1 R/S分析法

R/S分析法，也称重标极差分析法，是20世纪英国水文学家Hurst提出的，经过Mandelbrot（1972，1975）、Mandelbrot、Wallis（1969）和Lo（1991）等人的研究逐步完善。R/S分析法认为人类水事活动能使流域水文过程序列的分形特征值、赫斯特指数、分形维数发生明显变化，可通过赫斯特指数判断水文过程的变异点[3]。

1）R/S分析法处理序列值

一时间序列：ξ1，ξ2，ξ3，…，ξn，对应的时间为t1，t2，t3，…，tn。将此连续时间序列抽出一个时间尺度的序列ξ1，ξ2，ξ3，…，ξn，序列的时间跨度为τ=tN-t1，在时间τ内，该序列的平均值为：

式中：N为时间序列的长度。

在tj时刻，序列值ξi相对于其平均值＜ξ＞Ni的累积偏差为：

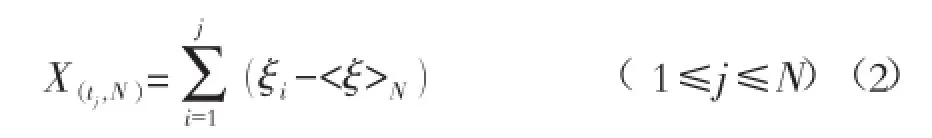
同一个N值所对应的最大X（t）值和最小X（t）值之差为极差，并记为：

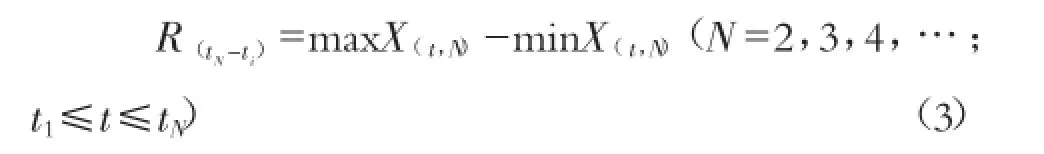
Hurst利用的标准偏差为∶

2）Hurst指数

以ln（R/S）为纵坐标，lnτ为横坐标，作线性回归图，图形是一簇斜率为H、过定点（lnc，0）的直线。通过ln（R（τ）/S（τ））=Hlnc+Hlnτ计算H。

分别以ξi（i=10，11，12，…，n-10）为分界点将数据分为两部分，对这两部分进行R/S分析，相应的H记为H1和H2，求出H1和H2之差的绝对值△H=|H1-H2|，△H最大的一点为变异最大的点，即可相应找出变异年份[3]。

2 滑动平均相关系数法

相关分析法反映2个系列间统计相依程度，以一个步长在2个相关水文序列上滑动得到相关序列，新序列若有变异点，则有一个或者两个能发生变异，若没有变异点，不能直接确定2个序列是否存在变异。滑动相关系数法是一种综合诊断方法，求多组相关联的序列的滑动相关系数序列，诊断出新序列的变异点，变异点反映每组序列相关程度的变化情况，从而得到2个序列的可能变异点，综合分析可得径流序列的变异点[4]。

先求出2个序列（P1，P2，P3，…，Pm）与（W1，W2，W3，…，Wm）的相关系数r1，然后再求（P2，P3，P4，…，Pm+1）与（W2，W3，W4，…，Wm+1）的相关系数r2，…，rn，得到一个相关系数序列，其中m≥10。

对m取多个值（取m=a），可以更有效地寻找变异点，并最终得到a个相关系数序列，并以时间为横坐标，滑动相关系数为纵坐标绘制曲线，得到a条滑动相关系数曲线。将a个相关系数序列求平均值得到另一组滑动相关系数序列，绘制滑动相关系数系列平均值与时间的曲线。分析观察这a条曲线以及滑动相关系列平均值与时间的曲线，便可得到变异点。相关系数采用皮尔逊相关系数，其求解方程式为：

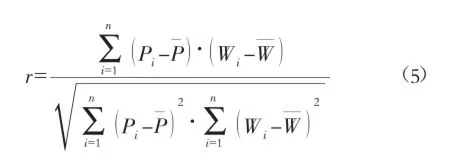
相关系数r的取值在-1.0～+1.0之间。r＞0时，两变量呈正相关，越接近于1.0，正相关越显著；r＜0时，两变量呈负相关，越接近于-1.0，负相关越显著；r=0时，则两变量相互独立[4]。

3 实例

3.1 概况

陡河位于燕山南部，介于沙河、还乡河之间，河道地势落差大，形式陡峭，独流入海，全长120 km，流域面积1 340 km2。陡河水库位于唐山市东北15 km处，控制流域面积530 km2，总库容为5.152×108m3，是以防洪为主并为城市生活和工农业供水的大型水库，也是引滦入唐工程的终端水利枢纽工程。流域内地形比较复杂，坡陡流急，陡河流域处于半干旱温带季风气候区内，季节变化明显，受季风气候影响，多年平均降水量671 mm，降水年际变化大，年内分配不均匀，年降水量的80%集中在6至9月份[6]。

3.2 基本资料

本文采用了陡河水库流域以上1953—1999年共47年的降雨和径流资料，其中降雨序列是通过陡河流域17处雨量站点实测资料，结合使用泰森多边形法计算得到的，径流序列是根据陡河水库管理中心提供的《陡河水库以上流域年径流分析》摘取的。径流量用水量平衡法还原，还原公式为：

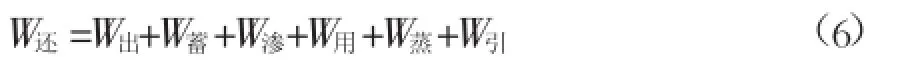
式中：W还为还原年径流量；W出为陡河水库实测出库流量；W蓄为陡河水库年蓄变量；W渗为陡河水库年渗漏水量；W用为工农业及生活用水量；W蒸为陡河水库蒸发损失水量；W引为跨流域引水量[7]。见表1。

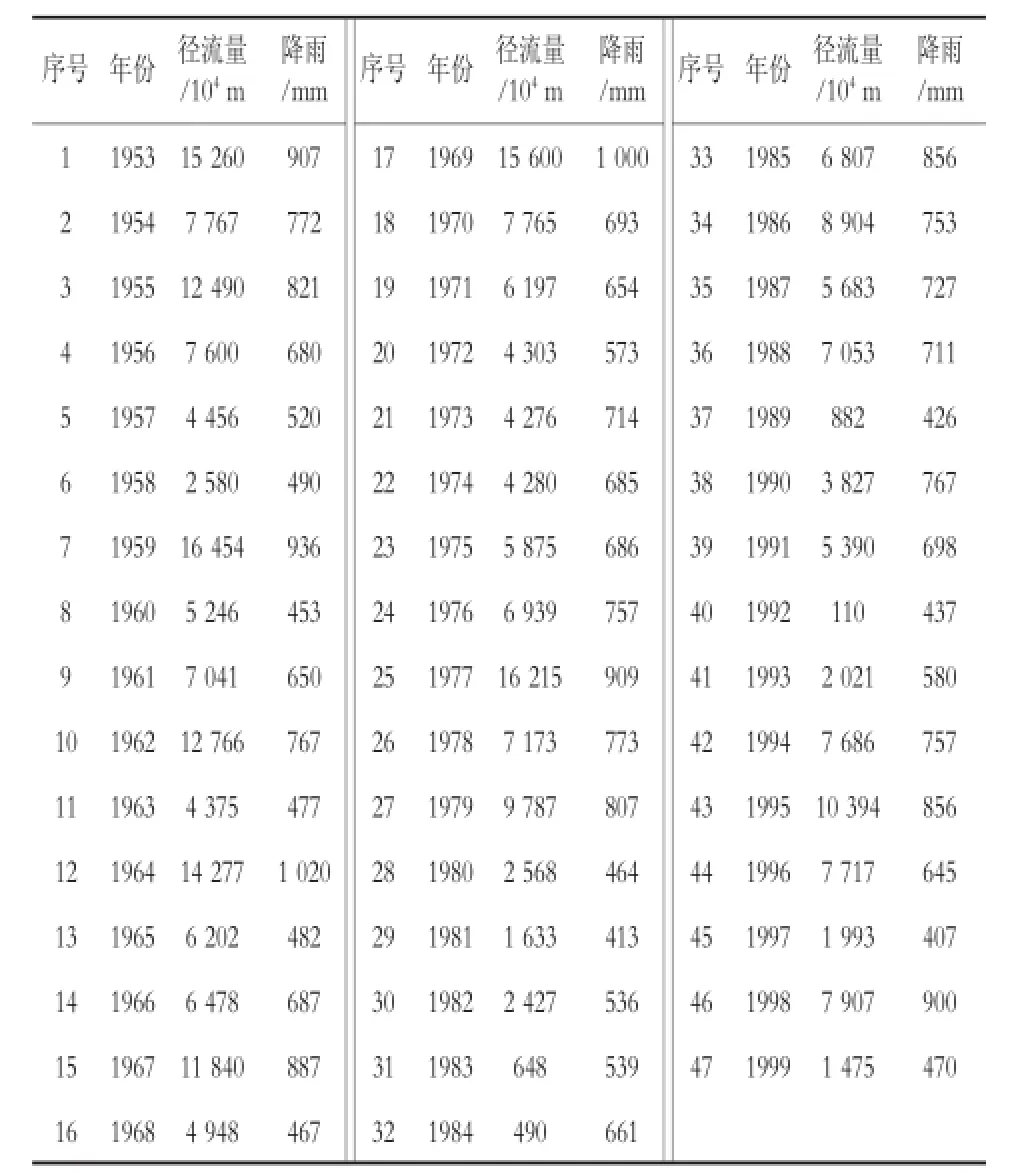
表1 陡河水库1953—1999年还原总水量

3.3 R/S法分析降雨和径流序列变异点

使用R/S法分别对陡河水库流域以上1953—1999年共47年的资料序列进行分析，得到的△H序列与时间变化的折线图，见图1，2。

图1 陡河水库降雨序列分段R/S分析图

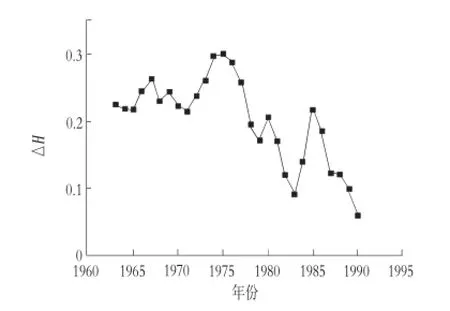
图2 陡河水库径流序列分段R/S分析图

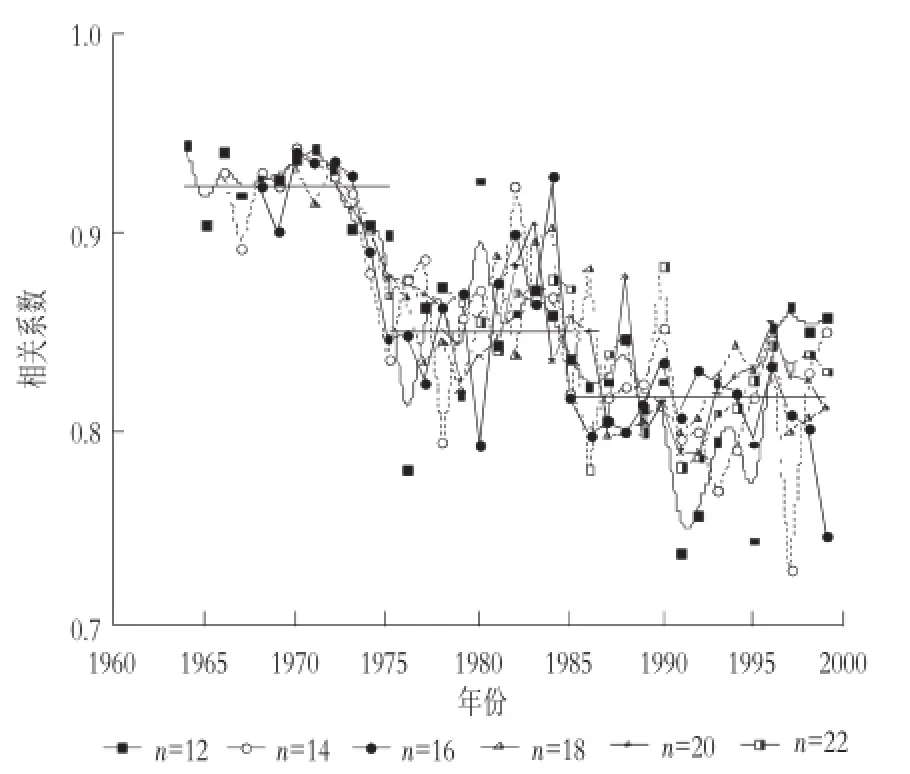
图3 陡河水库降雨—径流序6种步长滑动相关系数序列值

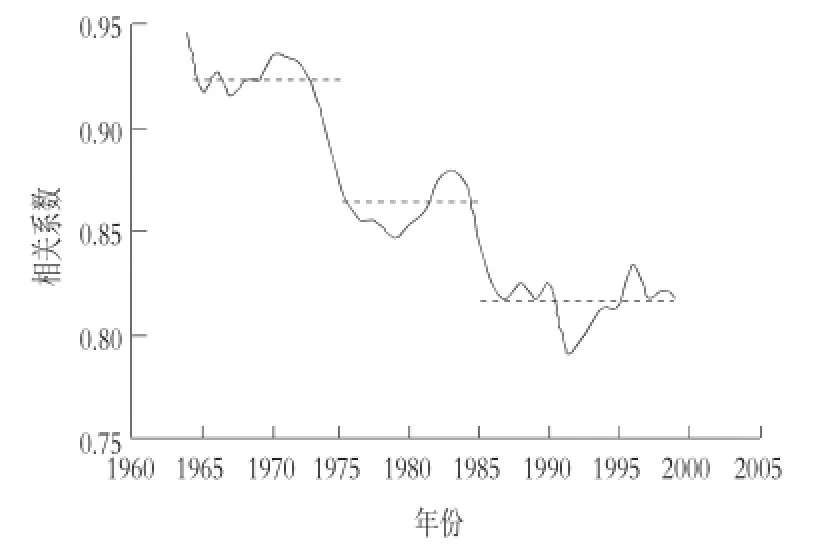
图4 陡河水库降雨—径流序6种步长滑动相关系数序列平均值

1）从R/S法分析降雨的变异点来看，降雨的最大△H在1975年，次大△H分别在1967年和1980年；1963—1975年的△H的数值普遍偏大，且变化不大；1975—1990年，△H最大值在1980年，△H值普遍偏小，降雨系列比较明显的变异点在1975年。

2）从R/S法分析径流的变异点来看，径流量的最大△H在1975年，次大△H分别在1967年和1966年；1963—1975年的△H的数值普遍偏大，△H的值都在0.2以上；1977—1990年△H普遍偏小，除1980年和1985年之外其余年份的△H都在0.2以下，其中1985年是1978—1990年的△H最大点，综合分析径流量的变异点在1975年以及1985年。

3.4 滑动相关系数法分析降雨和径流序列变异点

使用滑动相关系数法对陡河水库流域以上1953—1999年共47年的降雨—径流进行分析，以n=12，14，16，18，20，22为分段，得到6个降雨—径流皮尔逊相关系数序列，以及这个6个相关系数的平均值，并以相关系数为纵坐标曲线，以时间为横坐标做相关系数曲线图以及相关系数平均值曲线图，见图3，4。

观察陡河水库1953—1999年的降雨—径流6种步长（n=12，14，16，18，20，22）滑动相关系数序列值与时间的曲线图，同时观察降雨—径流各步长滑动相关系数序列的平均值与时间的曲线图，可以看出降雨—径流的皮尔逊相关系数按时间分布被1975年和1985年分为3个取值范围，1960—1975年，皮尔逊相关系数的值在0.925上下浮动；1975—1985年，皮尔逊相关系数的值在0.875上下浮动；1985—1999年，皮尔逊相关系数的值在0.82上下浮动。综合分析，陡河水库流域以上降雨—径流系列的变异点发生在1975年以及1985年。

3.5 结果分析

利用R/S法与滑动平均系数法分析陡河水库流域降雨系列、径流系列、降雨—径流相关系列，分析得出陡河水库降雨系列的变异点是1975年；径流系列的变异点是在1975年和1985年；降雨—径流皮尔逊相关系数的变异点在1975年和1985年。

结合实际情况分析，为满足工农业生产不断发展的需要，70年代初开始，水利工程建设掀起高潮，人们在陡河流域建立了许多中、小型水库，灌渠，水闸，扬水站，提引水工程等，变异点发生在1975与实际情况吻合。

根据陡河水库管理中心提供的资料，1980—1984年由于降水偏少，同时地下水开采过量，导致了1984年较1977年地下水位下降了10 m左右，后几十年由于降水偏丰，地下水位有所回升。所以径流系列，以及降雨—径流相关系数的变异点发生在1985年也与实际情况吻合。

［1］成静清.非一致性年径流序列频率分析计算［D］.陕西：西北农林科技大学，2010：1—117.

［2］沈宏.天然径流还原计算方法初步探讨［J］.水利规划与设计.2003（3）：15—18，47.

［3］周蓓，刘俊民，等.RS法在径流还原和预测中的应用［J］.人民长江，2008，39（15）：42—45.

［4］陈广圣，王义民，等.基于滑动相关系数法的流域径流变异诊断［J］.自然灾害学报，2016，25（1）：11—17.

［5］刘志涛，程兵峰.近10年陡河水库来水变化趋势及其影响因素分析［J］.海河水利，2011（4）：36—38.

［6］刘素英.陡河流域雨、水情分析［J］.河北水利科技，1999，20（1）：12—16.

［7］魏茹生.径流还原计算技术方法及其应用研究［D］.陕西：西安理工大学，2008：1—103.

TV121

A

1002－0624（2017）04－0018－03

2016-11-09