一道直线与椭圆有公共点问题的多种解法

■重庆市铁路中学校 何成宝

题目：设直线l:y=kx-2和椭圆y2=1有公共点,求k的取值范围。

解法一：(判别式法)

把直线l的方程y=kx-2代入椭圆方程,消去y,整理得:

(2k2+1)x2-8kx+6=0。

由Δ=(-8k)2-24(2k2+1)≥0,解得k≥或k≤-。

所以,直线l与椭圆有公共点时,k的取值范围为。

点评:判别式法是处理直线与圆锥曲线位置关系时最常用的方法,方法较简单,但运算较复杂。

解法二：(三角代换法)

把椭圆+y2=1的参数方程,代入直线l的方程得:

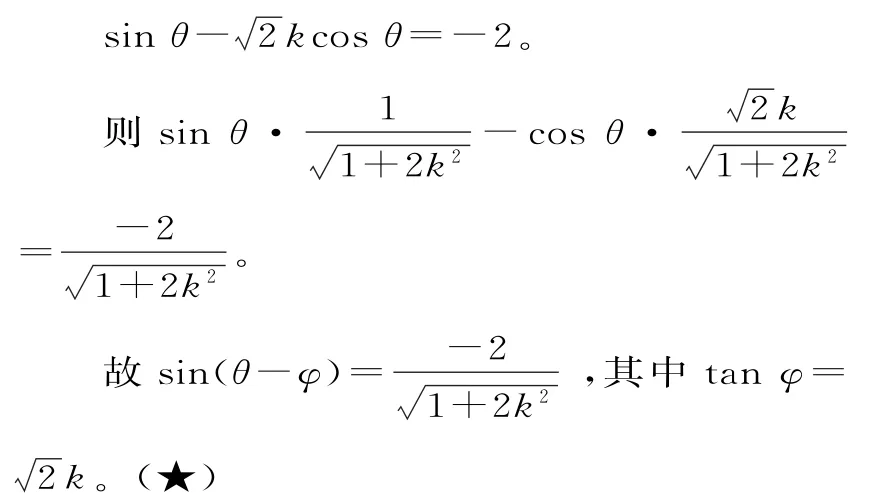
由题意可知关于θ的方程(★)有解,故≤1,1+2k2≥4。

解得k≥或k≤。

所以,直线l与椭圆有公共点时,k的取值范围为。

点评:通过三角代换把关于x,y的方程问题转化为关于θ的方程问题,对于直线、曲线有公共点的问题,用此方法往往能收到事半功倍的效果。

解法三：(数形结合法)

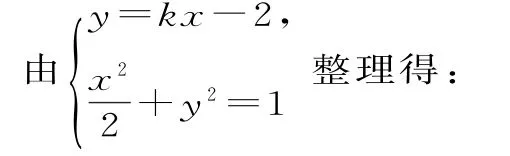
(2k2+1)x2-8kx+6=0。

若直线l与椭圆只有一个公共点,则Δ=(-8k)2-24(2k2+1)=0,解得k=或k=。如图1,直线l:y=kx-2恒过点P(0,-2),所以,直线PA的斜率为,直线PB的斜率为

由图可知,直线l与椭圆有公共点时,k的取值范围为。

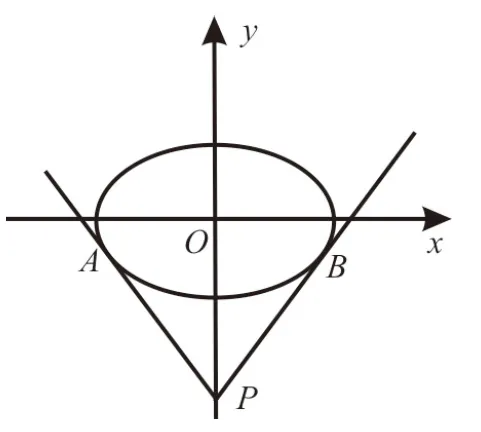
图1

点评:通过数与形的结合,可以把抽象的问题具体化,复杂的问题简单化。