椭圆中的热点题型

■甘肃秦安县第二中学 罗文军

题型一：椭圆的定义及其标准方程

椭圆焦点位置与x2,y2系数间的关系:给出椭圆方程=1时,椭圆的焦点在x轴上⇔m＞n＞0;椭圆的焦点在y轴上⇔0＜m＜n。

若点P为椭圆C1(a＞b＞0)上一点,F1,F2为椭圆C的两焦点,由椭圆的定义得,|PF1|+|PF2|=2a。

已知椭圆=1(a＞b＞0)的左右两焦点分别为F1、F2,AB是过C的焦点F1的弦,△F2AB的周长是20,椭圆C的离心率为e=,则椭圆C的方程为_____。

解：由已知及椭圆的定义可得:

△F2AB的周长为|AB|+|AF2|+|BF2|=|AF1|+|AF2|+|BF1|+|BF2|=4a=20,所以a=5。

又离心率e=,所以c=4,b2=a2-c2=9。

所以椭圆C的方程为=1。

题型二：椭圆的几何性质

离心率是圆锥曲线的重要几何性质,此类问题一般有两类:一类是根据一定的条件求椭圆的离心率;另一类是根据一定的条件求离心率的取值范围。无论是哪类问题,关键是借助图形建立关于a,b,c的关系式(等式或不等式),转化为e的关系式。

已知椭圆标准方程为=1(a＞b＞0),它的左焦点F(-c,0)关于直线bx+cy=0的对称点P在椭圆上,则椭圆的离心率是( )。

解：设焦点F(-c,0)关于直线bx+cy=0的对称点为P(m,n)。

整理得,4e6+e2-1=0,将各选项代入知e=符合,故答案为D。

题型三：直线与椭圆的位置关系

判断直线与椭圆的位置关系可使用代数法,即通过方程研究,先将直线方程与椭圆的方程联立,消去一个未知数y(或x),得到关于x(或y)的一个一元二次方程。由于该一元二次方程有无实数解、有几个实数解与方程组的解的个数相对应,故可利用一元二次方程根的判别式Δ进行分析,根据Δ＞0,Δ＜0还是Δ=0即可判断方程组解的个数,从而得出直线与椭圆的交点情况。

求椭圆弦长的方法:联立直线与椭圆的方程,消元得到关于一个未知数的一元二次方程,利用弦长公式:|P1P2|=,其中x1,x2(y1,y2)是上述一元二次方程的两根,由根与系数的关系求出两根之和与两根之积后代入公式可求得弦长。

解决椭圆的中点弦问题有两种方法:法一是把直线的方程和椭圆方程联立消去一个未知数,利用根与系数的关系和中点坐标公式来解决;法二是点差法,设出两个交点坐标,代入椭圆方程,整体作差,结合中点坐标公式解答。

已知椭圆C=1(a＞b＞0),右焦点为F(c,0),A(0,2),且|AF|=,椭圆的离心率为。

(1)求椭圆C的标准方程;

(2)设直线l的方程为y=kx+m,当直线l与椭圆C有唯一公共点M时,作OH⊥l于H(O为坐标原点),若|MH|=|OM|,求k的值。

解：(1)因为|AF|=c2+4=7,所以c=。又,故a=2,b2=a2-c2=1。

故椭圆C的标准方程为+y2=1。

(2)设M(x0,y0),由意题知|OH|=|OM|。

题型四：椭圆中的定值问题

椭圆中的定值问题常见类型及解题策略:

(1)求代数式为定值问题。依题意设条件,得出与代数式参数有关的等式,代入代数式,化简即可得出定值。

(2)求点到直线的距离为定值问题。利用点到直线的距离公式得出距离的关系式,再利用题设条件化简,变形求得。

(3)求某线段长度为定值问题。利用长度公式求得关系式,再依据条件对关系式进行化简、变形即可求得。

定值问题必然是在变化中所表示出来的不变的量,常表现为求一些直线方程、数量积、比例关系等的定值。解决此类问题常从特征入手,求出定值,再证明这个值与变量无关。

已知椭圆Γ=1(a＞b＞0)的右焦点为F(1,0),椭圆Γ的左,右顶点分别为M,N。过点F的直线l与椭圆交于C,D两点,且△MCD的面积是△NCD的面积的3倍。

(Ⅰ)求椭圆Γ的方程;

(Ⅱ)若CD与x轴垂直,A,B是椭圆Γ上位于直线CD两侧的动点,且满足∠ACD=∠BCD,试问直线AB的斜率是否为定值,请说明理由。

解：(Ⅰ)因为△MCD的面积是△NCD的面积的3倍,所以MF=3NF,即a+c=3(a-c),所以a=2c=2,b2=3。

故椭圆Γ的方程为=1。

(Ⅱ)∠ACD=∠BCD,则kAC+kBC=0。

设直线AC的斜率为k,则直线BC的斜率为-k。

不妨设点C在x轴上方,C,设A(x1,y1),B(x2,y2),则AC的直线方程为y-=k(x-1),代入=1中整理得:

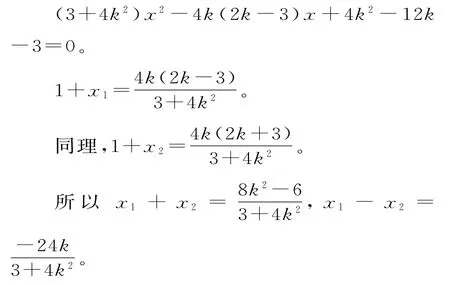
故kAB=因此直线AB的斜率是定值。