聚焦高考中简易逻辑的经典问题

■陕西省洋县中学 刘大鸣(特级教师)

高考对简易逻辑的考查主要以 “命题的四种形式及真假的判断、充分必要条件的合理判断及与创新题交汇、含简单的逻辑联结词的命题真假判断、命题的否定、复合命题真假的判断及应用”等经典问题呈现,凸显简易逻辑的工具性及交汇性。

聚焦1 命题的四种形式

(2015年山东高考卷)设m∈R,命题“若m＞0,则方程x2+x-m=0有实根”的逆否命题是( )。

A.若方程x2+x-m=0有实根,则m＞0

B.若方程x2+x-m=0有实根,则m≤0

C.若方程x2+x-m=0没有实根,则m＞0

D.若方程x2+x-m=0没有实根,则m≤0

解析：在大前提的条件下利用原命题的逆否命题的定义进行改写,命题的逆否命题是将原命题结论的否定作为条件,将原命题条件的否定作为结论,故选D。

感悟：在写四种命题时,首先,把大前提保留,其次,要把原命题写成“若p,则q”的形式,要注意分清原命题的条件p与结论q,逆命题需把条件与结论对调,否命题需把条件与结论都进行否定,逆否命题需把原命题的条件与结论都否定并对调。

变式1 (2017年江苏省泰州中学高三模拟卷)命题“若x2+3x-4=0,则x=-4”的逆否命题及其真假性为( )。

A.“若x=-4,则x2+3x-4=0”,为真命题

B.“若x≠-4,则x2+3x-4≠0”,为真命题

C.“若x≠-4,则x2+3x-4≠0”,为假命题

D.“若x=-4,则x2+3x-4=0”,为假命题

解析：根据逆否命题的定义可以排除A,D。因为x2+3x-4=0,所以x=-4或1,故原命题为假命题,逆否命题也为假命题,选C。

聚焦2 四种命题的真假判断

(2014年陕西高考卷)原命题为＜a,n∈N,则{a}为递减数n+n列”,关于其逆命题、否命题、逆否命题真假性的判断依次如下,正确的是( )。

解析：利用四种命题之间的关系,研究原命题和逆命题的真假。若＜an,n∈N+,则an+1＜an,{an}为递减数列,原命题为真命题,故其逆否命题也是真命题。原命题的逆命题:若 {an}为递减数列,n∈N+,则＜a,该命题为真命题,原命题的否n命题也为真命题,故选A。

A.真,真,真 B.假,假,真

C.真,真,假 D.假,假,假

感悟：判断一个命题的真假,用直接法判定命题为真命题,需要严格的推理过程,由命题条件推出结论正确;要判定一个命题为假命题,只需举出一个反例就行;当判断某个命题的真假无从入手或比较繁杂时,可依据“原命题与逆否命题同真同假,逆命题与否命题同真同假”判断其逆否命题的真假性,称为等价转化法。

变式2 (2017年全国大联考)原命题“a,b为两个实数,若a+b≥2,则a,b中至少有一个不小于1”,下列说法错误的是( )。

A.逆命题为:若a,b中至少有一个不小于1,则a+b≥2,为假命题

B.否命题为:若a+b＜2,则a,b都小于1,为假命题

C.逆否命题为:若a,b都小于1,则a+b＜2,为真命题

D.a+b≥2是a,b中至少有一个不小于1的必要不充分条件

解析：由a+b≥2可以得到a,b中至少有一个不小于1,但a,b中至少有一个不小于1不一定能得出a+b≥2,所以原命题为真,逆命题为假,则逆否命题为真,否命题为假,命题的否定形式为假,A、B、C选项都正确。而对于选项D,a+b≥2是a,b中至少有一个不小于1的充分而不必要条件,故选项D说法错误。

聚焦3 充分条件与必要条件的判定

(2017年天津高考卷)设θ∈R,则”是“sinθ＜”的( )。

A.充分而不必要条件

B.必要而不充分条件

C.充要条件

D.既不充分也不必要条件

解析：本题考查绝对值与三角不等式有关的充分条件与必要条件的判断,判断充分性可用正弦函数的单调性,⇔0＜θ＜,由正弦函数在区间(0 ,)上单调递增,可得sinθ＜;必要性不成立,令θ=π,sinθ＜,不满足。则“”是“sinθ＜”的充分而不必要条件,故选A。

感悟：充要条件的判断有“定义法”、“集合法”、“等价命题转化法”,要注意所涉及知识点的含义,坚持“双向推理”的原则,能推出一定要说明原因,推不出要举出反例。命题否定形式的充要条件的判断,一是从反面入手,利用原命题与逆否命题的等价性,二是要对逻辑联结词“或”“且”深刻理解,并在分清条件和结论的基础上推理判断。

变式3 (2017年原创押题预测卷)已知数列{an},{bn}满足bn=an+an+1,则“数列{an}为等差数列”是“数列{bn}为等差数列”的( )。

A.充分而不必要条件

B.必要而不充分条件

C.充要条件

D.既不充分也不必要条件

解析：若数列{an}为等差数列,设其公差为d1,则bn+1-bn=(an+1+an+2)-(an+an+1=an+2-an=2d1,所以数列{bn}是等差数列;若数列{bn}为等差数列,设其公差为d2,则bn+1-bn=(an+1+an+2)-(an+an+1)=an+2-an=d2,不能推出数列{an}为等差数列,所以“数列{an}为等差数列”是“数列{bn}为等差数列”的充分不必要条件,选A。

聚焦4 充分、必要条件与新定义交汇

(2011年湖北高考卷)若实数a,b满足a≥0,b≥0,且ab=0,则称a与b互补。记φ(a,b)=-a-b,那么φ(a,b)=0是a与b互补的( )。

A.充分而不必要条件

B.必要而不充分条件

C.充要条件

D.既不充分也不必要条件

解析：依据新定义和充分、必要条件的判断方法,进行推理。充分性,由φ(a,b)=0可得=a+b,ab=0,故a,b中至少有一个为0。不妨设a=0,代入=a+b,可得=b,故b≥0,满足互补定义,则a与b互补。必要性,实数a,b满足a≥0,b≥0,且ab=0,则a=0或b=0,不妨设a=0,所以φ(a,b)=-a-b=-b=0;同理b=0时,φ(a,b)=0。综上可知,φ(a,b)=0是a与b互补的充要条件,选C。

感悟：对新定义与充分、必要条件的判断,首先分析新定义的特点,把新定义所叙述的问题的本质弄清楚,并能够应用到充分、必要条件的判断过程之中,这是破解新定义型问题的关键所在。

变式4 (2007年湖北高考)若数列{an}满足=p(p为正常数,n∈N*),则称{an}为“等方比数列”。甲:数列{an}是等方比数列;乙:数列{an}是等比数列。则甲是乙的( )。

A.充分而不必要条件

B.必要而不充分条件

C.充要条件

D.既不充分也不必要条件

解析：由等比数列的定义知,若乙:{an}是等比数列,公比为q,则,则甲命题成立;反之,若数列{an}是等方比数列,即=q2,故=±q,公比不唯一,不符合等比数列定义,则命题乙不成立,故选B。

聚焦5 对含有逻辑联结词的命题真假的判断

(2017年山东高考卷)已知命题p:∃x∈R,x2-x+1≥0;命题q:若a2＜b2,则a＜b。下列命题为真命题的是( )。

A.p∧q B.p∧﹁q

C.﹁p∧q D.﹁p∧﹁q

解析：先确定命题的形式,再判断命题的真假,最后按真值表确定复合命题的真假。特称命题p为真找到一个值即可,当x=0时x2-x+1≥0成立,知p是真命题。命题q为全称命题,不成立可举反例,由12＜(-2)2,1＞-2可知q是假命题。由命题和命题的否定一真一假知,﹁q为真,由真值表可得p∧﹁q是真命题,故选B。

感悟：全称命题为真时需证明,为假时举反例即可;特称命题为真时需举一个例子,为假时要证明全称命题为真。复合命题的真值表可记为:有真“或”为真,有假“且”为假,命题和命题的否定一真一假。

变式5 (2017年原创押题预测卷)已知命题p:∃x0∈R,sinx0+cosx0=;命题xq:函数f(x)=-()有一个零点,则下列命题为真命题的是( )。

A.p∧q B.p∨q

C.﹁q D.p∧(﹁q)

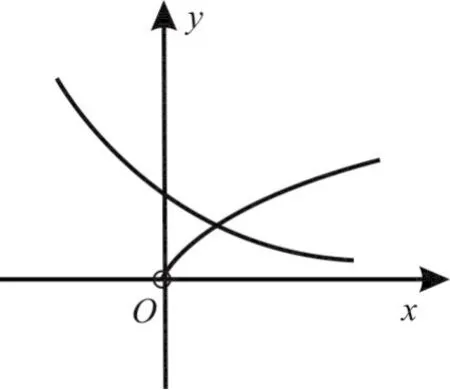
图1

解析：因为sinx+cosx=2sin(x +) ∈[-2,2],所以命题p是假命题。在同一直角坐标系下作出函数y=与的图像,如图1所示。由图1知,两个函数的图像只有一个交点,所以函数f(x)的零点只有一个,故命题q是真命题,所以p∨q是真命题,选B。

聚焦6 根据命题的真假性求参数的可能取值

(2017年北京高考卷)能够说明“设a,b,c是任意实数,若a＞b＞c,则a+b＞c”是假命题的一组整数a,b,c的值依次为_____。

解析：证明不等式恒成立为假命题,可取一组特殊值,如-1＞-2＞-3,但-1+(-2)=-3,所以验证是假命题。

感悟：对于不等式恒成立问题的判断,一般采用举反例法。解答本题时可利用赋值的方式,举反例进行验证,答案不唯一。

变式6 (2017年湖南郴州质检卷)若命题p:“∃x0∈R,使2x0-2≤a2-3a”是假命题,则实数a的取值范围是_____。

解析：“∃x0∈R,使2x0-2≤a2-3a”是假命题,等价于∀x∈R,2x-2＞a2-3a恒成立。由函数2x-2的值域知,只需-2≥a2-3a,解之得1≤a≤2,即实数a的取值范围是[1,2]。

聚焦7 全称量词和存在量词的否定

(2016年浙江高考卷)命题“∀x∈R,∃n∈N*,使得n≥x2”的否定形式是( )。

A.∀x∈R,∃n∈N*,使得n＜x2

B.∀x∈R,∀n∈N*,使得n＜x2

C.∃x∈R,∃n∈N*,使得n＜x2

D.∃x∈R,∀n∈N*,使得n＜x2

解析：∀的否定是∃,∃的否定是∀,于是“∀x∈R,∃n∈N*,使得n≥x2”的否定是∃x∈R,∀n∈N*,使得n＜x2,故选D。

感悟：对含有存在(全称)量词的命题进行否定,需要 “改量词,否结论”,即把全称量词与存在量词互换,然后否定原命题的结论。

注意命题的否定与否命题的区别:“否命题”是对原命题“若p,则q”的条件和结论分别加以否定而得到的命题,它既否定其条件,又否定其结论;“命题的否定”,只是否定命题的结论,含量词时切记“全称量词”与“存在量词”互换,含联结词时注意“且”与“或”的互换。

变式7 (2017年湖南张家界二模)命题“∀n∈N,f(n)∉N且f(n)≤n”的否定形式是( )。

A.∀n∈N,f(n)∈N且f(n)＞n

B.∃n0∈N,f(n0)∈N且f(n0)＞n0

C.∀n∈N,f(n)∈N或f(n)＞n

D.∃n0∈N,f(n0)∈N或f(n0)＞n0

解析：∃n0∈N,f(n0)∈N与f(n0)＞n0至少有一个成立,故选D。

聚焦8 由含量词的命题的真假求参数的最值或取值范围

(2015年山东高考卷)若“∀x∈,tanx≤m”是真命题,则实数m的最小值为______。

解析：求含量词的不等式恒成立问题中的参数范围,可合理转化为求正切函数的值域。

若“∀x∈,tanx≤m”是真命题,则m≥f(x)max,其中f(x)=tanx,x∈

函数f(x)=tanx在上为增函数,故f(x)max=1,m≥1,m的最小值为1。

感悟：全称命题中的不等式恒成立问题,可合理利用正切函数的性质求值域,意在考查同学们综合利用所学知识解决问题的能力,凸显等价转化思想的具体应用。

变式8 (2017年山东潍坊联考)已知m∈R,命题p:∀x∈[-1,1],x2-2x-4m2+8m-2≥0成立;命题q:∃x∈[1,2],(x2-mx+1)＜-1成立。如果“p∨q”为真,“p∧q”为假,求实数m的取值范围。

解析：若p为真:∀x∈[-1,1],4m2-8m≤x2-2x-2恒成立。

设f(x)=x2-2x-2,配方得f(x)=(x-1)2-3,所以f(x)在[-1,1]上的最小值为-3。因此,4m2-8m≤-3,解得≤m。所以当p为真时,≤m≤。

若q为真:∃x∈[1,2],使x2-mx+1＞2成立,所以m＜在 [1 ,2]上能成立。

设g(x)==x-,易知g(x)在[1 ,2]上是增函数,所以g(x)的最大值为g(2)=,m＜,q为真时,m＜。

因为“p∨q”为真,“p∧q”为假,所以p与q一真一假。

综上所述,实数m的取值范围是