由递推公式求数列通项的常用方法
2017-04-28郑州市第十一中学1805班魏晨光
■郑州市第十一中学1805班 魏晨光
数列即按照一定顺序排列的一组数,其通项公式为数列{an}的第n项与序号n之间的关系式。而我们平常做题中经常会给出一个递推公式,以此来求解数列{an}的通项公式,那么由递推公式求数列通项的常用方法有哪些呢?
一、累加、累乘法
1.已知a1,且an-an-1=fn(),n∈N*,则用累加法求解an。

已知数列{an}满足a1=3,anan-1=2(n-1),n∈N*,求an的通项。
解析:由累加法可知an=(an-an-1)+(an-1-an-2)+…+(a3-a2)+(a2-a1)+a1=2[1+2+…+(n-1)]+3。
解得an=n(n-1)+3,n∈N*。
二、构造法
由an+1=kan+f(n),k≠1,派生出的几种情况。
1.形如f(n)=d(d为常数),即an+1=ka+d。通过观察探究,令,得a+λ=n+1k(an+λ)为一个新的数列{An},n∈N*。
且{An}是以a1+λ为首项,公比为k的公比数列,由此求出 {An}的通项,进而求出{an}的通项。
2.形如f(n)=kn+b,即an+1=kan+kn+b,求通项方法如下。
不妨设an+1+x(n+1)+y=c(an+xn+y)。
解出k,b。再代入原式得到数列{An},其首项为a1+x+y,公比为c,进而求出{an}的通项。
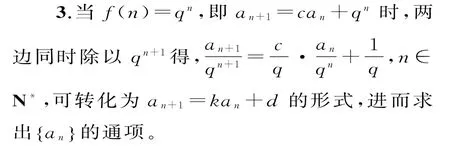
4.形如an+2=kan+1+dan时,如何求?
设an+2-xan+1=y(an+1-xan),则:解得,。xy
可得到一个新的等比数列{An},进而求解{an}的通项。
三、取倒数法
形如an+1=(a,b,c为常数),两边同时取倒数。
若a=c,则可以直接得出为等差数列,公差为。若a≠c,利用上文构造新的数列,可求解。
练一练:
1.已知数列{an}前n项和为Sn,a1=2,且Sn=+n+1,n∈N*,求解an通项。
2.已知数列{a}中,a=2,a=n∈N*,求解an通项。
