何直观 建立模型思想
——《两积之和》拓展课案例分析
2017-04-28吴玉兰
吴玉兰
【课前思考】
浙教版四年级的应用问题单元,出现了这样的应用问题:“一个篮球95元,一个足球75元。买5个篮球与2个足球共需要多少元?”“如果篮球的单价是95元,买5个篮球和2个足球共用去625元。1个足球多少元?”这两题用算术方法解决,分别是“95×5+75×2”“(625-95×5)÷2”。仅从这两个算式上看,似乎没有什么联系,但实际上,这两题的基本结构都是“a×b+c×d=f”,我们把这样的应用问题称为“两积之和”。它们的区别在于前一题是f未知,我们称之为正向题;后一题是等式左边的一个量未知,为前一题的逆向题。对于这一类题,结合数量关系来进行分析与解答,在解决逆向问题时很难建立总量与部分量之间的关系,无法感知正向与逆向题之间的基本结构是一致的。尤其在情境变得复杂以后(如鸡兔同笼),更难分析量与量之间的关系。
模型思想的建立是学生体会和理解数学与外部世界联系的基本途径,有助于学生提高学习数学的兴趣与应用意识。对于“两积之和”这一内容,可以借助图形让学生直观感知各个量之间的关系,并通过观察比较,发现正向与逆向两种题型的基本结构其实是一样的,建立“a×b+c×d=f”的基本模型,理解虽然情境在变、已知与未知量在变,但基本结构不变,并能用这样的模型来解决实际问题。同时,在这一过程中体会模型的建立能帮助我们解决一类问题,培养几何直观,建立模型思想。
【教学过程】
一、图形引入,初步感知
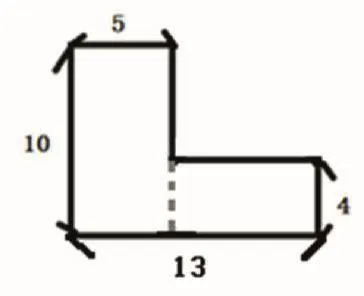
1.看图求面积(单位:厘米)。
师:这儿有一个图形,你能求出它的总面积吗?
(学生口头列式,教师板书:6×4+7×10=94)

出示第二个图形,在学生回答的基础上板书:10×5+8×4=82。

出示第三个图形,在学生回答的基础上板书:10×5+(13-5)×4=82。
2.观察比较。
师:通过观察发现了什么?
生:都是左边长方形的面积+右边长方形的面积=总面积。
生:都是先用乘法求出两个长方形的面积,再把两部分的积加起来求和。
生:我还发现第三题和第二题其实是一样的,只是第二题右边长方形的长是已知的,第三题右边长方形的长需要我们先求出来。
3.揭示课题:像这样先分别求积,再求两部分的和,我们可以把它称为“两积之和”。
(板书:a×b+c×d=f两积之和)
【设计意图:对于学生来说,图形比较直观,利于模型的建立。因此,本环节从求组合图形的总面积引入,通过观察、对比,发现三道题的图形在变化,已知量在变化,但求面积的基本方法不变,都是“左边长方形的面积+右边长方形的面积=总面积”。从计算方法上来看,都是先求积,再求出两部分的和,从而得出“两积之和”的基本模型“a×b+c×d=f”。同时,题组中第三题的呈现,又可以让学生体会到虽然其中的一个量没有直接告知,需要先求,但基本结构仍然不变。这样的设计,使两积之和”模型的建立经历了从图形模型到代数模型的过程,借助几何直观把复杂的数学问题变得简明、形象,使模型的建立也有了依托,更利于学生理解。】
二、变化沟通,寻找联系
1.变化图形。
(将上面的三幅图变化为下面的图)
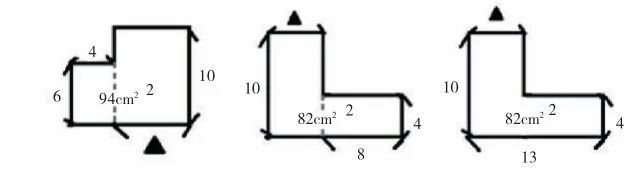
师:哪里变了?
生:原来是求总面积,现在总面积已知,求的是其中一条边的长度。
师:现在你还能写出像这样的两积之和的等式吗?
2.独立研究。
(1)写一写:看图写出两积之和的等式。
(2)想一想:为什么这么列式?
(3)找一找:这三题有什么相同与不同?
3.集体交流。
(1)交流第一题。
生:(94-4×6)÷10。
生:4×6+10×▲=94。
师:你支持哪一种?为什么?
生:第二种。因为第二种还是 a×b+c×d=f,是两积之和。
师:那这两种方法之间有联系吗?
生:94就是面积和,去掉4×6可以得到右边长方形的面积,再除以宽就是要求的长。
生:其实第一种方法就是来求第二种方法里的▲。也就是(f-a×b)÷d=c。
师:你们真会观察。看来,只要列出了两积之和的等式,我们就可以用第一种方法来求出图形代表的数。
(2)交流剩下两题。
生:第二题是10×▲+8×4=82,10×▲是左边长方形的面积,8×4是右边长方形的面积,合起来就是总面积82。
生:第三题我们是10×▲+(13-▲)×4=82,可以在这里加一条虚线,就把这个图形分成了两个长方形,左边是10×△,右边长是(13-▲),宽是 4,分别求出面积后再加起来就可以了。
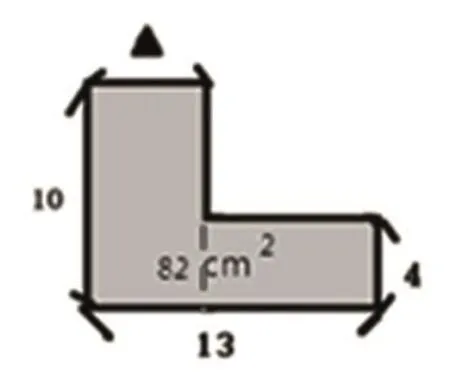
生:我们有不一样的方法,13×4+(10-4)×△。
师:这种方法可以吗?他又是怎么分这个图形的?你可以手势表示一下吗?
(课件演示虚线分割)

师:是这样吗?现在你能解释这个等式的意思吗?说给同桌听一听。
生:我还有不一样的方法。我是 13×10-(10-4)×(13-▲)=82。
师:这又是怎么得到的?你能想象出图吗?
(在学生表述的基础上课件演示补的过程,并请学生解释等式的意思)

师:这种方法与前两种有什么区别?
生:前面都是分割后求面积和,现在是补上一块,用大面积减去补的部分的面积。
生:前面都是两积之和,最后一种方法不是了。
师:如果我们也给这类等式取个名字,你打算叫它什么?
生:两积之差。
4.前后比较,寻找异同。
(1)将两个题组一起呈现,进行比较。


师:这是我们刚才研究的两组题,请你仔细观察一下,有没有发现什么?
生:第一组题是总面积不知道;第二组题总面积告诉我们了,是一条长或一条宽不知道。
生:这两组题都是a×b+c×d=f,只是未知数的位置在变化。
师:看来,不管要求的是谁,这两组题的基本结构都是两积之和,我们都可以列出两积之和的等式来解决。
【设计意图:本环节将上一组题进行了已知与未知的变换,以列两积之和的等式。并通过这一题组与前一题组的对比,发现变化中的不变——基本结构仍然是“a×b+c×d=f”。体会到虽然问题在变复杂,但是结构不变,根据两积之和列出等式就能解决这样的问题,化难为易。同时,借助图形的直观性特点将抽象的数量关系与直观的图形有机结合,充分展现问题的本质,再次体会两积之和的基本模型“a×b+c×d=f”,感知模型的建立使问题的解决更为方便。这样的处理,帮助学生打开了数学的大门,突破了理解的难点。】
三、实际应用,体会价值
1.结合活动要求独立研究。
(1)★两种昆虫飞行速度和时间如下表,B昆虫飞行了多少分钟?
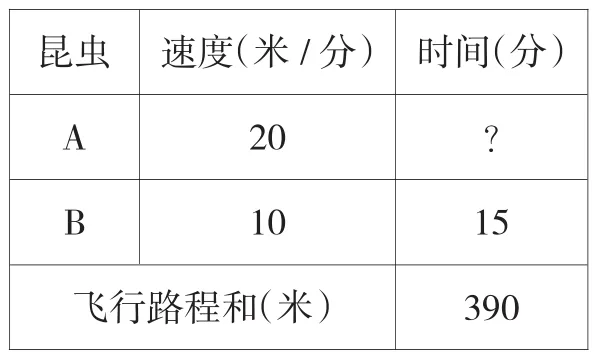
昆虫 速度(米/分) 时间(分)A 20 ?B 10 15飞行路程和(米) 390
(2)超市卖出一些鸡蛋和鸭蛋,共收入390元。其中鸡蛋每千克20元,鸭蛋每千克10元。鸭蛋卖了15千克,鸡蛋卖了多少千克?

(3)★★松鼠妈妈采松果,晴天每天可采20个,雨天每天只能采12个。松鼠妈妈一连采了8天,共采112个松果。这几天中下雨的有多少天?
①根据题中的信息,在图中标上数据。
②列出两积之和的等式。

(4)★★★根据上图,你还能编出怎样的应用题?试一试。
2.全班交流一星级题。
(1)汇报一星级两题。
(2)观察一星级两题,寻找联系与区别。
生:这两题用到的数都是一样的。
生:第一题中昆虫的速度相当于第二题鸡蛋与鸭蛋的单价;第一题中昆虫的飞行时间相当于第二题鸡蛋与鸭蛋的质量;第一题飞行的总路程等于第二题的总收入。
生:其实这两题的基本结构是一样的,都是两积之和。
师:那有不一样的地方吗?
生:每个数表示的意义不一样。比如20,第一题表示A昆虫的速度,第二题表示鸡蛋的单价。
(3)将一星级第二题的图变为下图:你能根据图编道应用题吗?现在两积之和的等式又可以怎么列?

3.分析二星级题。
生:原来鸡兔同笼也是两积之和。
师:是的,原来我们一直认为很难的“鸡兔同笼”问题也可以用两积之和来解决。
4.出示三星级题中标上数据以后的图。

师:根据这幅图,我们还能编出怎样的应用题呢?
【设计意图:从与图形相关的一个数学问题引入,基本模型建立后还需要与现实生活建立联系,体会到实际中的许多数学问题都可以用两积之和的模型来解决。因此本环节设计了分层的练习,通过比较,体会到虽然情境在变,求的量在变,但基本结构不变,题与题之间存在一定的相关性。同时,借助能见到的几何图形的形象关系产生对数量关系的直接感知,使抽象的数量关系形象化,实现代数问题与图形之间的互相转化,互相渗透,进一步体会现实世界中存在的许多数学问题都可以抽象成某种数学模型。对于学习能力比较好的学生,也安排了编题的练习,在变化中进一步体会基本结构的稳定性。】
