磁悬浮球控制系统的仿真研究

王玲玲，王 宏，梁 勇

(海军航空工程学院，山东 烟台 264000)



【信息科学与控制工程】

磁悬浮球控制系统的仿真研究

王玲玲，王 宏，梁 勇

(海军航空工程学院，山东 烟台 264000)

针对磁悬浮球系统的本质不稳定性，设计PID控制算法实现系统的稳定控制。建立磁悬浮球系统的动力学模型，并对其中的非线性部分进行平衡点处的线性化，采用根轨迹校正设计超前滞后控制器。最后采用PID控制设计，并使用根轨迹校正中零极点对系统性能影响的思想去调整PID参数，使系统的稳定性、动态性能和稳态性能满足要求。

磁悬浮球系统；PID；根轨迹法；校正

磁悬浮可以用于实现各种机械结构的高速、无摩擦运转，如高速磁悬浮列车、高速磁悬浮电机、磁悬浮轴承等。尽管磁悬浮的应用领域繁多，系统形式和结构各不相同，但究其本质都具有本质非线性、不确定性、开环不确定性等特征。这些特征增加了对其控制的难度，也正是由于磁悬浮的这些特性，使其更加具有研究价值和意义。本文针对磁悬浮球系统，研究其稳定控制，并使其性能指标满足要求。

1 磁悬浮球控制系统的基本原理

磁悬浮球控制系统主要由铁芯、线圈、光电源、位置传感器、放大及补偿装置、数字控制器和控制对象钢球等部件组成[1]，如图1所示。

当电磁铁上的线圈绕组通电时，位于磁场中的刚体受到电磁力的吸引作用。当产生的电磁力与球体的重力相等时，球体悬浮于空中，处于不稳定的平衡状态，当它受到外界扰动时，易失去平衡。因此，为了使系统稳定，就必须加上反馈环节，实现闭环控制，并设计控制算法，使稳定后的性能满足要求。

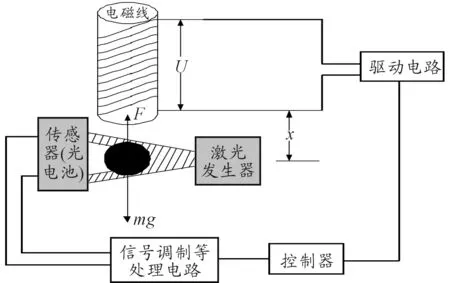
图1 磁悬浮球系统示意图

2 系统数学模型的建立

2.1 理论分析

如果忽略电磁铁的感抗对系统的影响，磁悬浮系统的数学模型可以完全由竖直方向运动方程和电磁力方程给出：

(1)

式中取向下方向为正。

(2)

F(i,x)为电磁力且为矢量(N)；x为小球质心到电磁铁磁极表面的瞬时气隙(m)；i为电磁铁绕组中的瞬时电流(A)；m为小球质量(kg)。

式(2)中，假设磁通在气隙处均匀分布，且电磁铁与球体组成的磁路的磁阻主要集中在气隙处；常系数K为与空气磁导滤等定参数相关的量[1-3]。

假设平衡点处小球的位移为x0，电磁铁线圈电流为i0，则平衡点处：

(3)

2.2 系统模型的线性化处理

对式(2)进行平衡点处的泰勒展开并线性化有

(4)

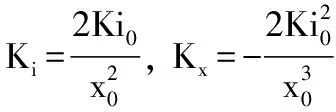
当定义系统输入量为电流，输出量为气隙，对上式两端进行拉式变换可得传递函数模型为

(5)

在实际系统中采用电压值表示对气隙和电流的控制，其中电压与气隙的关系需要通过传感器标定得出，其关系式为

Uo=Ksx

(6)

其中Ks为气隙与电压的关系系数(V/mm)。

而电压和电流的关系采用电压-电流型功率放大器表示，在功率放大器的线性范围内，可以将这种电压电流关系表示为：

(7)

其中，Ka为功率放大器的增益。

如此结合式(6)与式(7)，气隙-电流模型式(5)变为

(8)

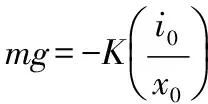
(9)

(10)

2.3 实际物理参数

表1给出具体参数值，当实验系统不同时，参数要重新测量。另外，即便针对同一套系统，如果更改平衡位置时，带有符号*的参数要根据实际进行测量和计算[1-3]。

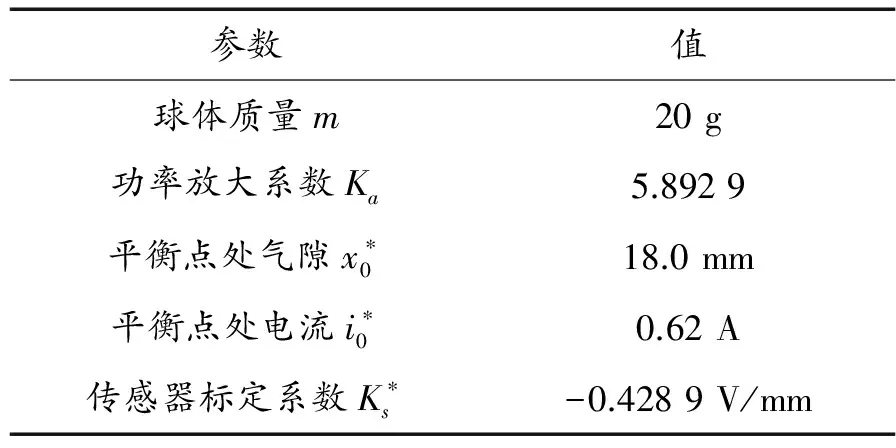
表1 系统的物理参数值

将参数代入式(9)与式(10)得到

(11)

(12)

可以看出系统有一个极点位于复平面的右半平面，根据系统稳定性判据，磁悬浮球系统是本质不稳定的。在Matlab中进行编程判断系统的可控性和可观性[4-7]，可以得到系统的可控矩阵和可观矩阵的秩为2，即系统状态可控矩阵的秩等于系统的状态变量维数，系统的输出可控矩阵的秩等于系统输出向量的维数，所以磁悬浮实验系统既是可控又是可观，因此可以对系统进行控制器设计，使系统稳定。

3 根轨迹控制设计

当系统的性能指标以时域指标提出时，可以借助根轨迹曲线获取校正装置的结构和参数。若期望主导极点在原根轨迹的左侧，则采用相位超前校正；若期望主导极点在原根轨迹上，则通过调整根轨迹增益，满足静态性能要求；若期望主导极点在原根轨迹的右侧，则采用相位滞后校正[8]。

3.1 使用根轨迹法设计磁悬浮球系统控制器

3.1.1 超前控制器的设计

设计控制器使得校正后的系统满足如下要求：调节时间ts≤0.2 s(2%)；超调量σ≤10%；稳态精度阶跃输入下ess≤0.05。按照超前校正的步骤，通过Matlab编程得到系统的串联超前校正控制器为

(13)

令输入为单位阶跃，得系统根轨迹如图2，单位阶跃响应如图3。

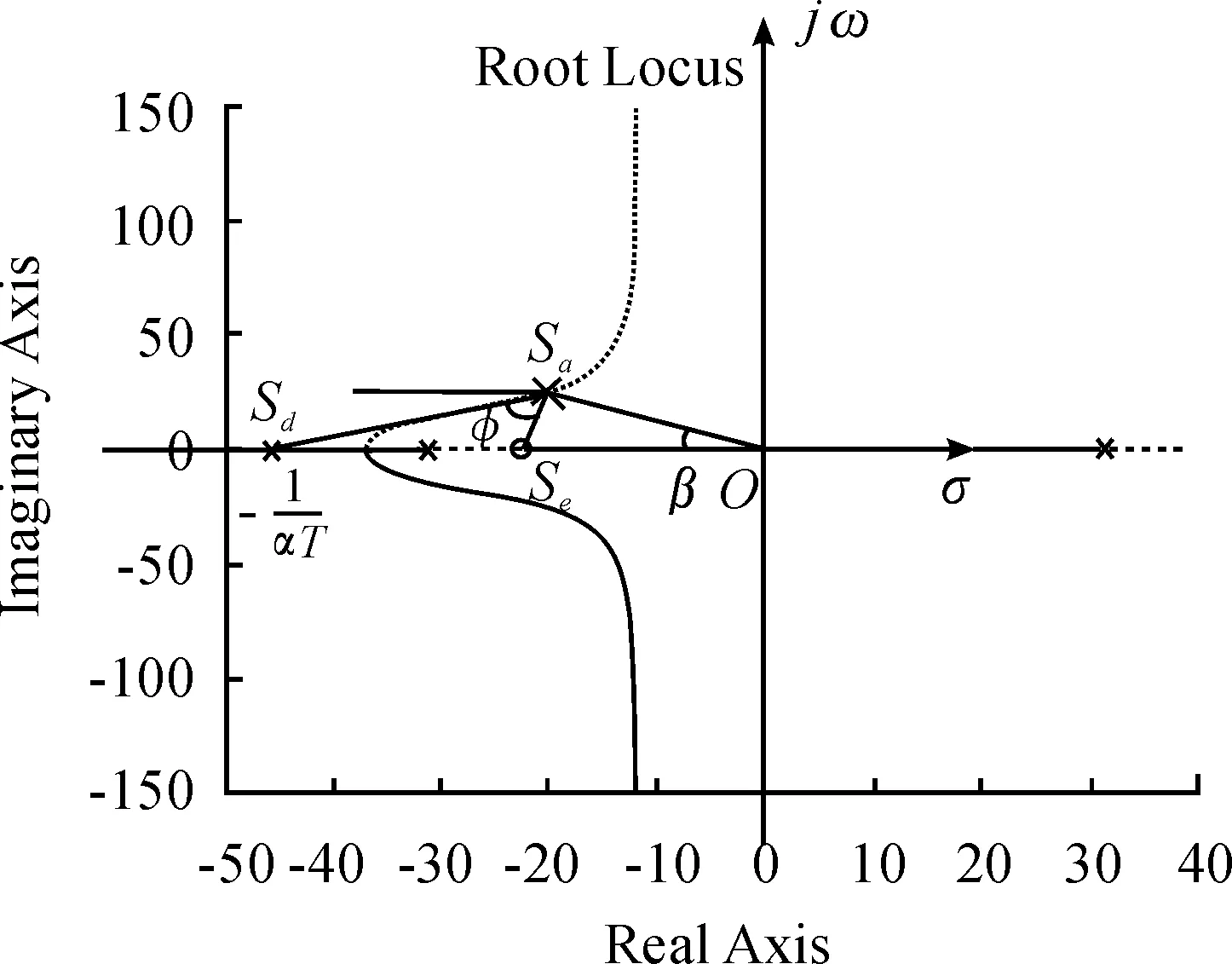
图2 磁悬浮系统超前校正后的根轨迹

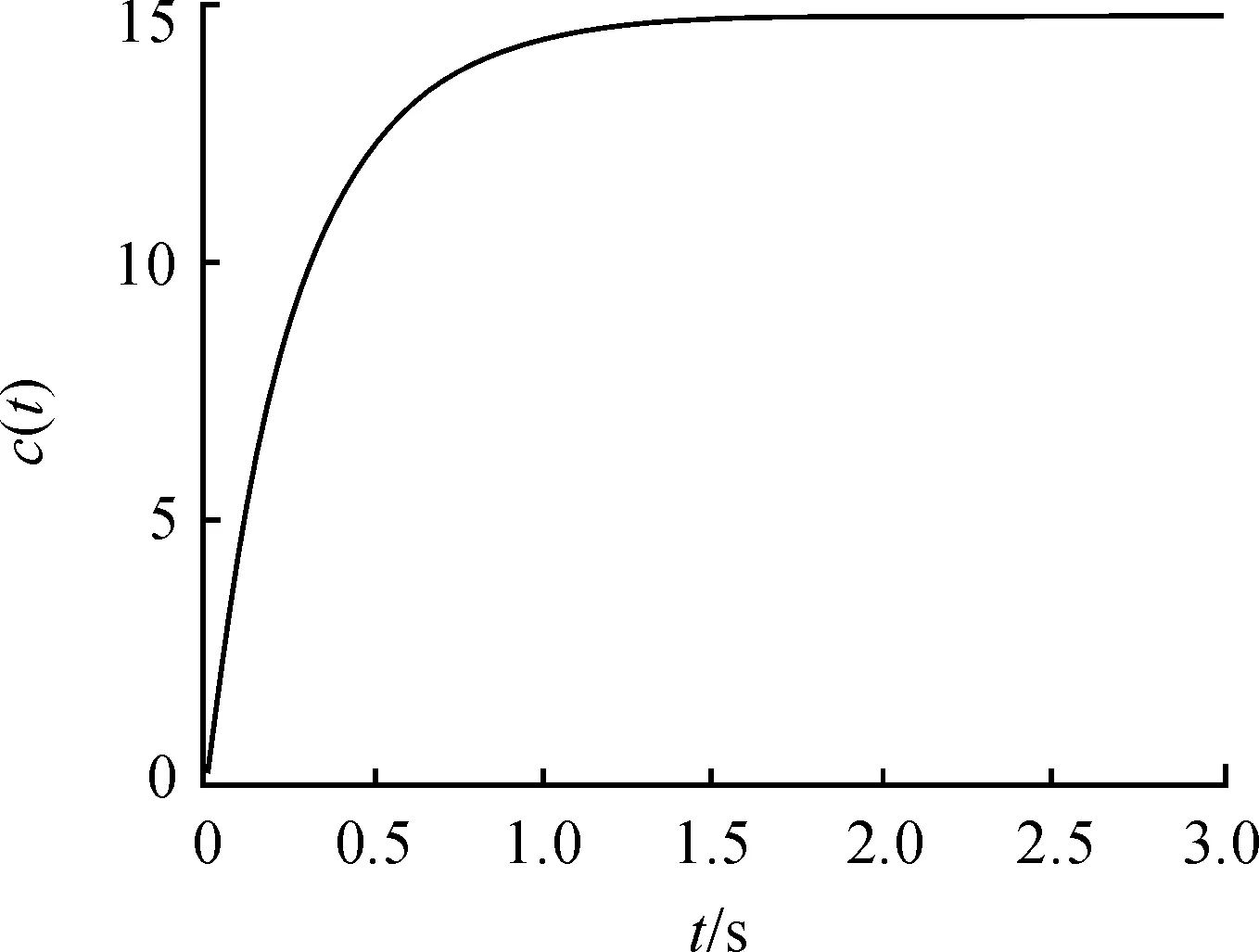
图3 一次超前校正后的单位阶跃响应

通过系统的阶跃响应可以分析得出：

1) 系统无超调，调节时间大约需要1.5 s，系统的稳态误差较大；

2) 在10%的超调要求下可设计出校正环节阶跃响应无超调，说明超前校正对系统的动态性能具有较好的调节作用。但过于平滑的过渡过程使系统的调节时间变慢，因此可以考虑适当降低过渡过程平稳性，使系统的调节过程加快；

3) 系统的静态误差较大，超前对于稳态误差的改善较弱，可以采用滞后装置改善。

3.1.2 滞后控制器的设计

通过上述一次超前校正，控制系统开环传函为

根据稳态指标的系统的静态误差系数K0≈20；代入滞后校正的设计公式

(14)

可得到b=0.053 64。

选取T值，可得到滞后网络传递函数。取T=3时，系统的根轨迹如图4。

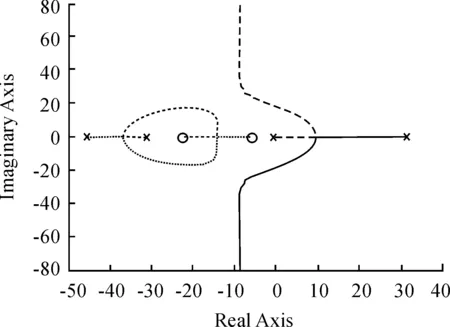
图4 超前滞后校正后的根轨迹

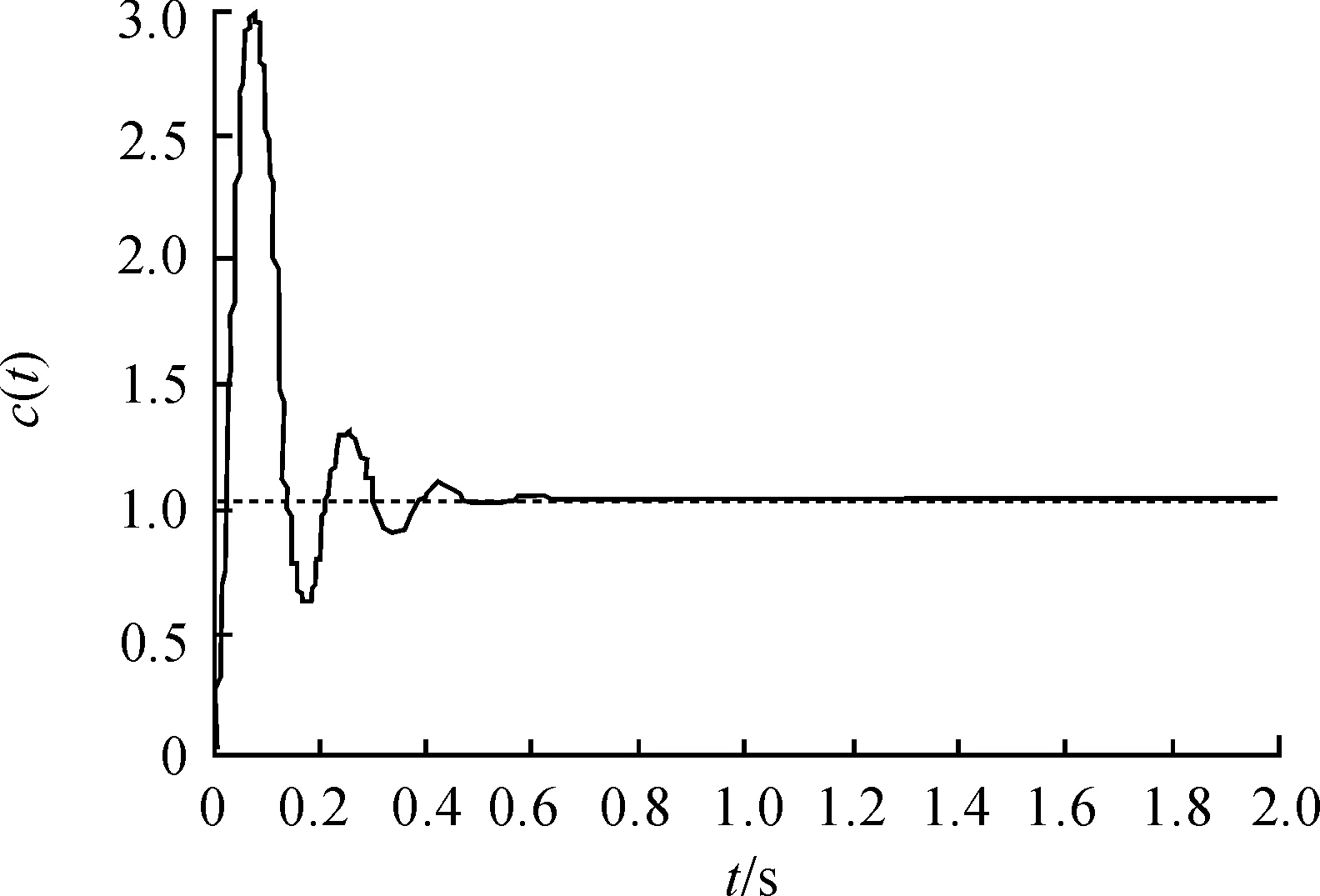
图5 多次超前滞后校正的单位阶跃响应

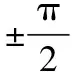
另外，在实际设计超前滞后网络时，应将其作为一个元部件设计，而不是把超前校正和滞后校正作为分离元件分别引入。

4 PID控制器的设计

利用Matlab中的Simulink设计含有PID控制器的闭环控制系统。其中,Kp为比例参数，Ki为积分参数，Kd为微分参数。

根据PID参数校正的方式，先将积分微分系数设为零，只调比例环节。当输出由发散调至等幅振荡时，Kp=0.6，如图6所示。从图中可以看出，在5 s内有约13.5个周期，故周期约为Pcr=6 s/13.5≈0.44 s。

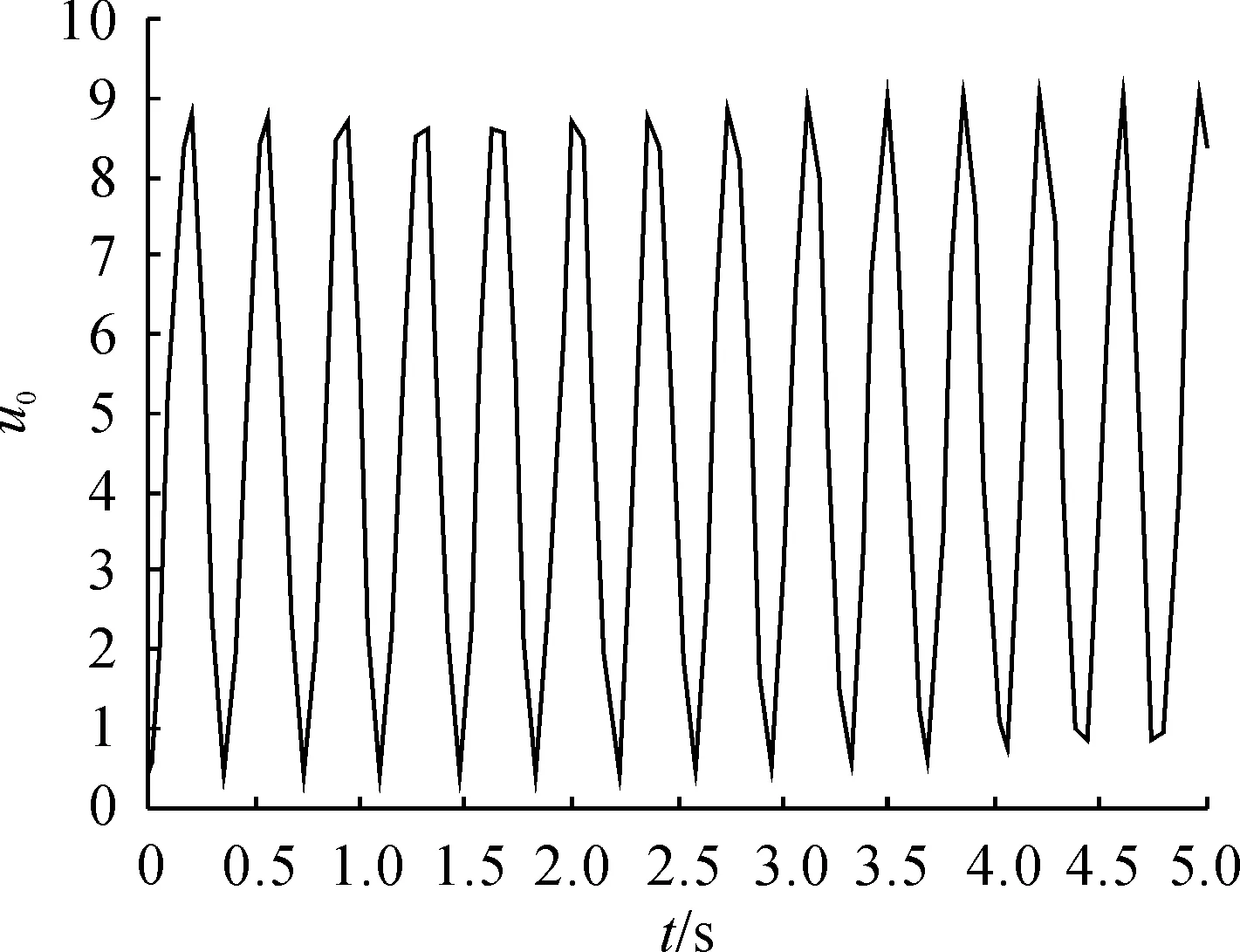
图6 Kp=0.6时的系统仿真图

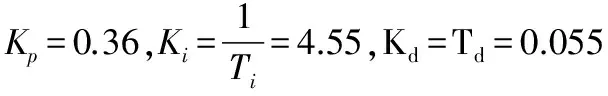
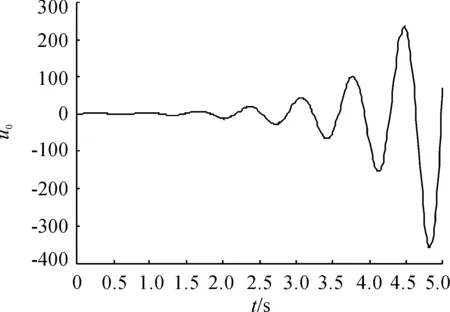
图7 Kp=0.36、Ki=4.55、Kd=0.055时

通过分析知道，PID控制器传函可以表示为

(15)

所增加的积分环节可以调整系统的稳态性能，增加两个开环零点可以调整系统的动态性能。其零点公式为

(16)

让附加的开环零点远离虚轴，最直接的方式就是增大Kp。当Kp增大至1.5时，系统响应曲线如图9所示，此时系统的超调过大。根据PID参数调节规则继续调节参数，当Kp=30，Ki=7，Kd=0.1时，系统仿真曲线如图10所示，系统的性能指标达到要求。

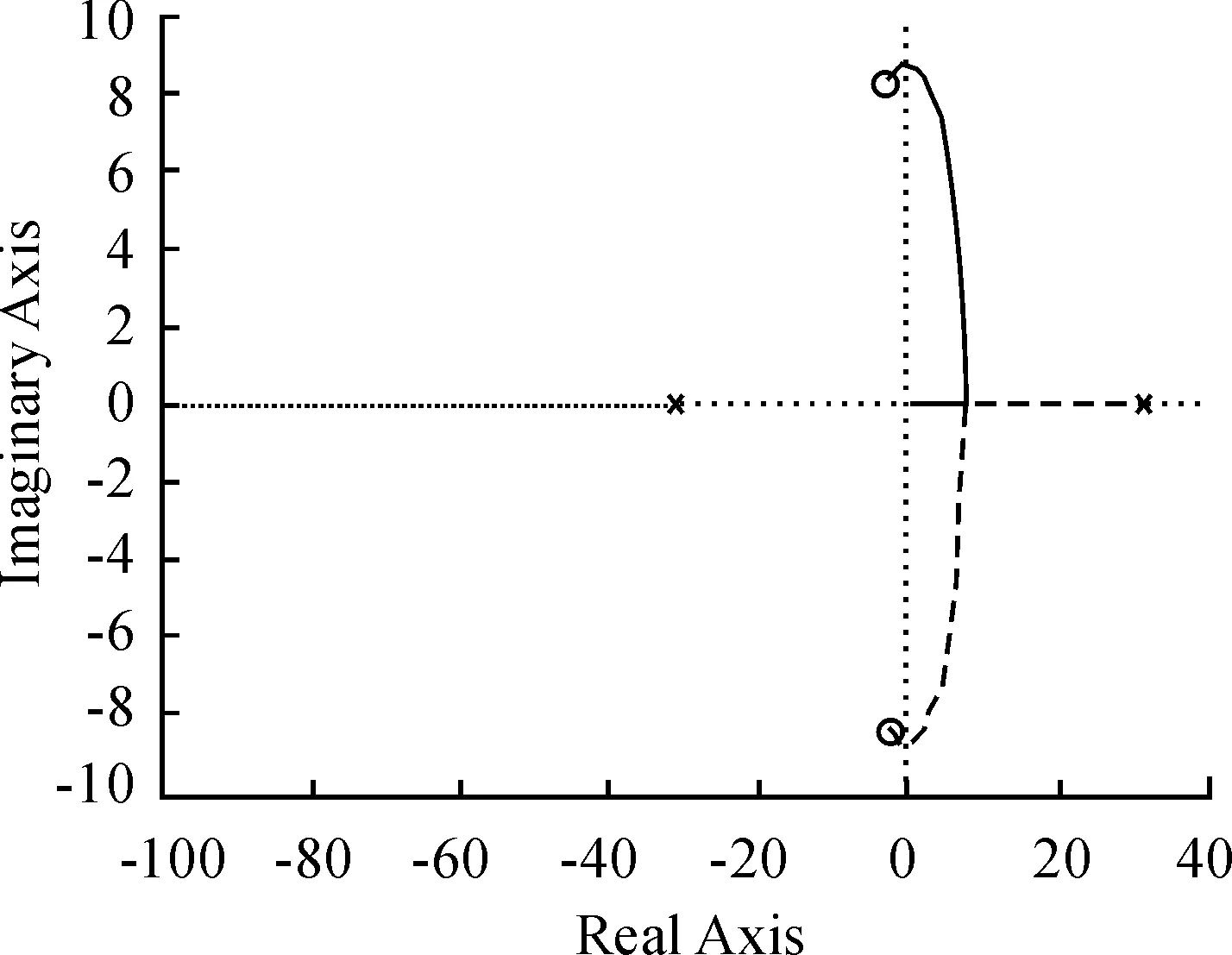
图8 Kp=0.36、Ki=4.55、Kd=0.055根轨迹图

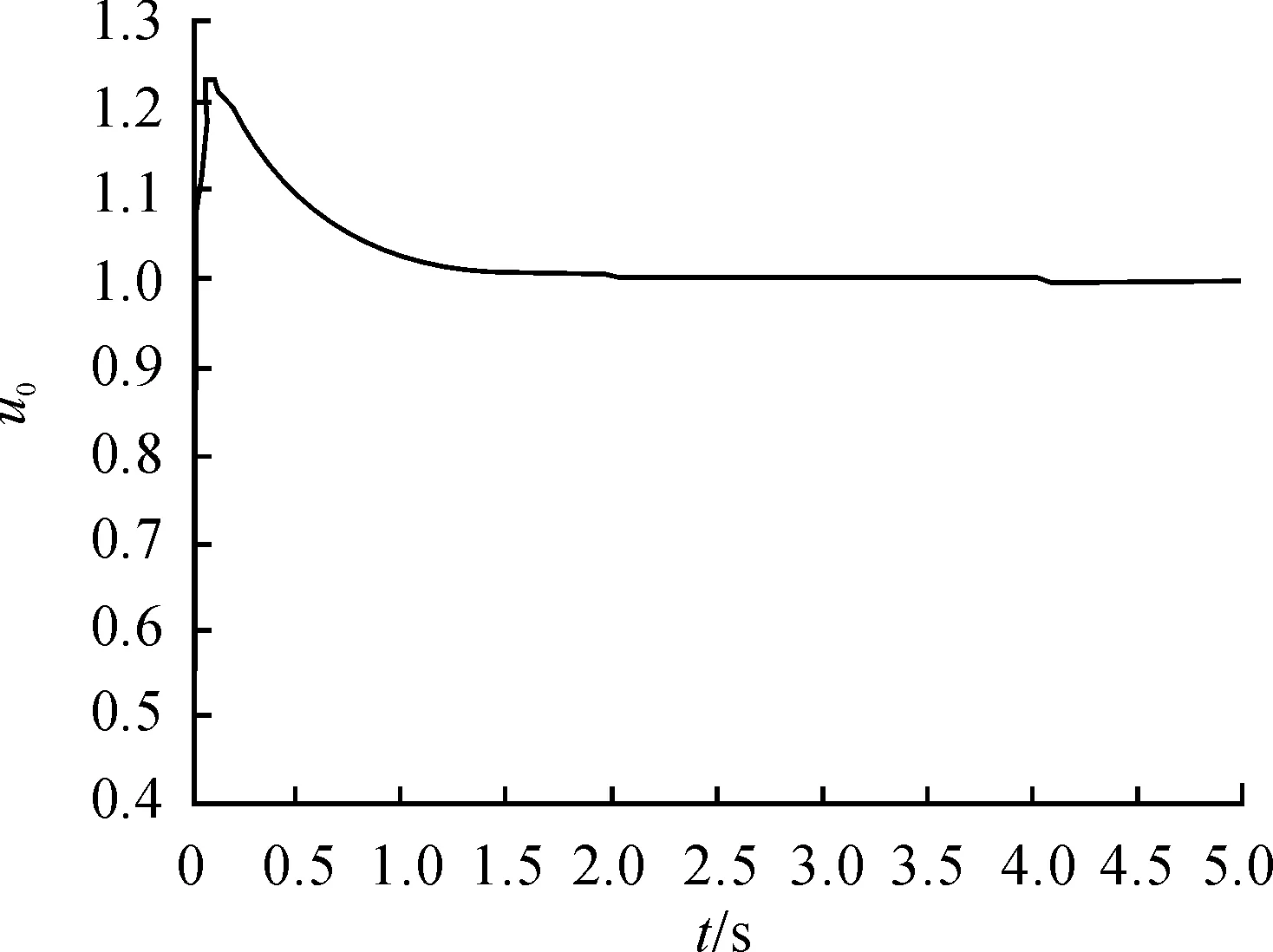
图9 Kp=1.5、Ki=4.55、Kd=0.055仿真图

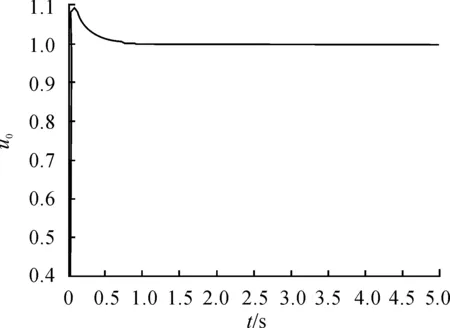
图10 Kp=30、Ki=7、Kd=0.1仿真曲线

将上述参数代入实验系统进行仿真，得到图11所示的仿真曲线，可以看出磁悬浮球系统在PID控制下可以实现稳定控制，终值范围在±0.01 mm间波动。当系统受到扰动时，可很快回复到平衡位置。

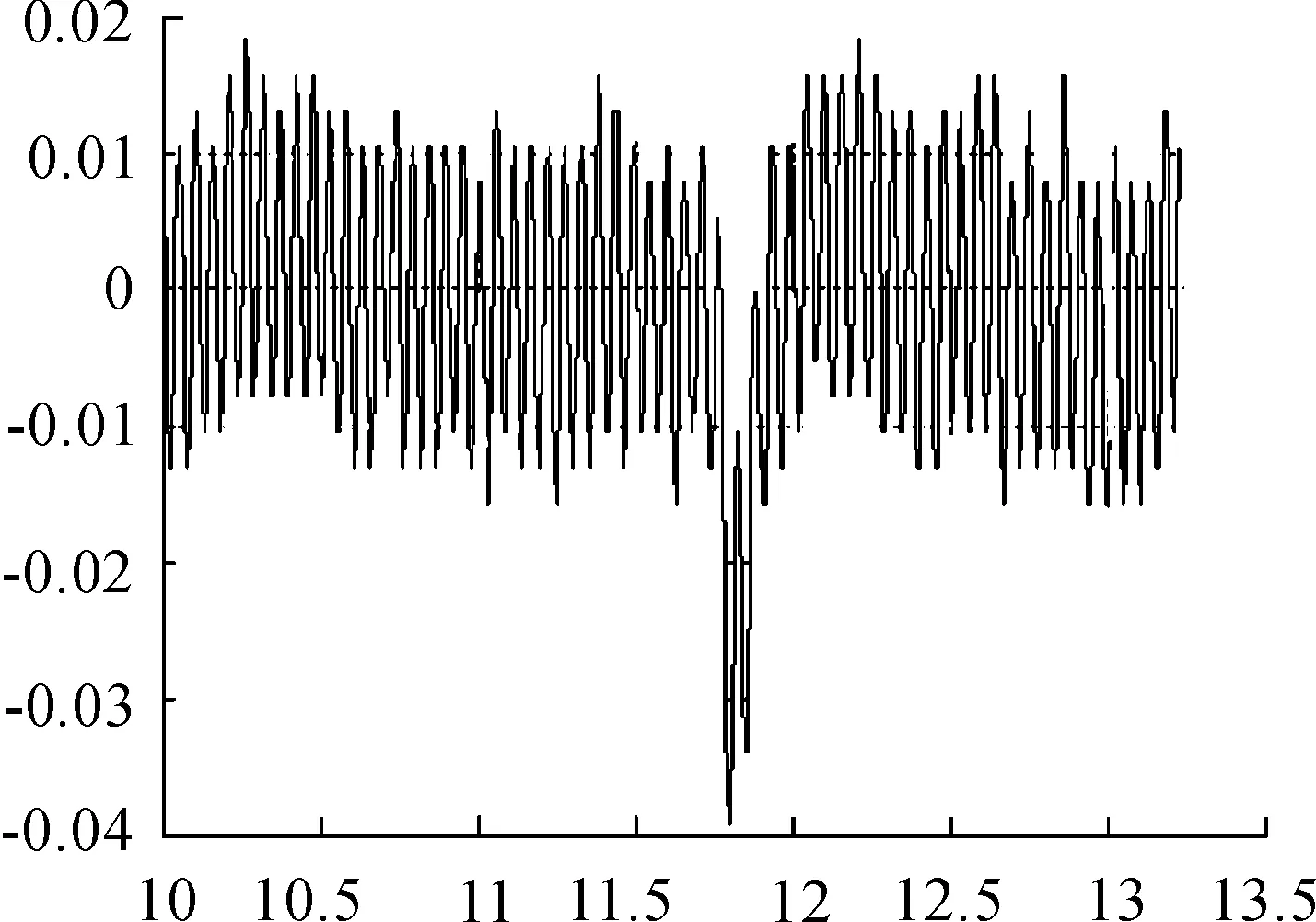
图11 磁悬浮球系统的半实物仿真曲线

5 结论

本文分析了磁悬浮球系统模型，并使用根轨迹方法进行了超前滞后控制器的设计。仿真表明超前滞后控制器仅可改善系统的稳定性，很难大幅改善动态性能。以根轨迹中开环零极点对系统性能影响的思路，设计PID控制器并进行参数调试，可以快速调整系统性能至最佳。

[1] 磁悬浮实验装置[R].固高科技(深圳)有限公司，2006.

[2] 张震.磁悬浮系统若干控制算法研究[D].上海：上海交通大学，2004年.

[3] 薛炜杰.基于MATLAB的磁悬浮控制系统研究[D].沈阳：东北大学，2008年.

[4] 张波，汤炳新.基于MatLab的磁悬浮球控制系统的设计[J].河海大学常州分校学报,2005,19(1):47-49.

[5] 张占军,林小玲.磁悬浮球系统控制器的分析设计[J].机电工程,2007,24(1):19-21.

[6] 吕辉榜，刘小静，卢长明.基于MATLAB的磁悬浮球实时控制设计及实验研究[J].仪表技术与传感器,2009(5):50-52.

[7] 彭辉，徐锦华，侯海良.模糊控制在磁悬浮球系统实时控制中的应用[J].控制工程,2009,16(3):278-281.

[8] KATSUHIKO OGATA.现代控制工程[M].4版.北京：电子工业出版社，2013.

(责任编辑 杨继森)

Simulation and Research of Magnetic Levitation Ball Control System

WANG Ling-ling, WANG Hong, LIANG Yong

(Naval Aeronautical and Astronautical University, Yantai 264000, China)

In order to solve the nature unstable feature of the magnetic levitation ball system, PID control algorithm was designed to realize the stability of the system. But traditional method for parameters adjustments had some subjectivity. Firstly, the dynamic model of the magnetic levitation ball system was established, and the nonlinear part of the system was linearized at the equilibrium point. Then the root locus method was used to design the lead lag compensator, and it was shown by the simulation results that the dynamic performance was difficult to meet the demands, although it can be stable. Thus PID control was adopted. And the thinking of the influence of open loop zeros and poles on root locus was adopted to correct parameters, which made the parameters adjustments have guidance. Finally the system was compensated to meet the requirements for stability, accuracy and swiftness.

magnetic levitation ball system; PID; root locus method; compensation

2016-11-26；

2016-12-26 作者简介：王玲玲(1984—)，女，硕士，讲师，主要从事控制技术研究。

10.11809/scbgxb2017.04.027

王玲玲，王宏，梁勇.磁悬浮球控制系统的仿真研究[J].兵器装备工程学报，2017(4):122-126.

format:WANG Ling-ling, WANG Hong, LIANG Yong.Simulation and Research of Magnetic Levitation Ball Control System[J].Journal of Ordnance Equipment Engineering,2017(4):122-126.

TP27

A

2096-2304(2017)04-0122-05