变形体超临界翼型动态气动特性
2017-04-28施文奎王元靖
施文奎, 王元靖, 张 兆
(中国空气动力研究与发展中心, 四川 绵阳 621000)
变形体超临界翼型动态气动特性
施文奎, 王元靖*, 张 兆
(中国空气动力研究与发展中心, 四川 绵阳 621000)
为实现飞行器外形根据来流条件变化做出相应调整,需深入了解变形体非定常气动现象和机理。以典型超临界翼型为研究对象,分别制定了翼型厚度及弯度变形方案,实现了翼型柔性变形。利用数值仿真方法在高雷诺数条件下开展了翼型厚度、弯度连续变形带来的非定常效应。结果表明,翼型厚度、弯度连续变形均会形成明显的升、阻力系数迟滞环,且频率越高、幅度越大,变形导致的非定常效应也越强;相对而言,翼型弯度变形产生的非定常效应较厚度变形产生的非定常效应更明显。最后通过分析流线图及压力系数分布图发现,流动结构随几何变形的迟滞性会导致非定常效应的产生。
超临界翼型;变形机翼;非定常效应;气动特性;流动结构
0 引 言
伴随科学技术的不断进步和发展,飞行器功能、性能和品质要求越来越受到关注。如今人们希望飞行器外形在飞行过程中根据来流条件的改变做出相应的调整,从而实现全飞行阶段性能最优[1-2],因此变形体飞行器技术逐步发展起来。但伴随飞机变形出现的气动外形变化与绕流结构之间的响应问题,会制约飞行器性能提升,甚至危及飞行安全。掌握超临界翼型变形与流动之间的响应规律,可为今后实现大型客机机翼变形打下基础,从而提升其经济型和安全性。
智能变形飞行器技术及相关研究在国外开展的较早,如美国NASA、DAPPA[3-5]机构,开展了大量可变形飞行器气动问题研究。Ajaj[6]等根据功能、操作和结构分布等对飞行器变形技术进行了分类,并且在功能单一化的变形技术基础上提出了连续变形理念。NEKOUBIN[7]针对跨声速条件下NACA0012翼型尾缘变形进行了数值计算,并对不同控制参数的影响作了说明。Walker[8]推导得出了简谐变形薄翼的非定常气动升力、阻力以及俯仰力矩,并以切比雪夫多项式的形式表达出来。Gandhi[9]等研究了变弯度机翼的蒙皮结构,Andersen[10]等理论推导得出了变尾缘翼型的动态失速模型。
国内相关研究起步较晚。徐国武[11]等给出了几种初步的翼型变形方案。郝南松[12]等用实验方法分析了低Re数下变弯度翼型准定常和非定常气动特性。陈钱[13]等研究了机翼两种变后掠大尺度全局变形方式对气动特性的影响,并且分析了气动特性机理。高彦峰等[14-15]利用解析解和离散涡的方法对可变形儒可夫斯基翼型亚声速、超声速情况下的非定常气动力做了详细研究。
以往对于变形机翼气动特性研究主要采用准定常方法,且研究集中在简单对称翼型上,对于跨声速条件下的超临界翼型研究较少。本文以RAE2822超临界翼型为对象,利用数值仿真方法重点研究了翼型厚度、弯度的变形幅度和变形频率对非定常气动力和流态结构的影响规律,并且通过分析流线图及压力系数分布图对非定常现象流动机理作了初步探索。研究结果可为今后超临界机翼变形技术提供技术支撑。
1 数值方法
1.1 计算模型
通过有限差分法离散N-S方程,非定常计算的时间离散采用双时间步法。翼型绕流问题采用远场边界条件。采用SA湍流模型计算。编写程序实现翼型厚度及弯度变形方案。
1.2 计算网格及算例验证
1.2.1 网格生成技术
采用C型网格(图1),941×144(流向×法向)。分成两个区域,其目的是防止由于远场端网格长细比过大导致网格变形时出现负体积,故只允许靠近翼型的网格变形。主要考察RAE2822翼型在高雷诺数全湍流情况下的气动特性,选取y+=25。计算得到网格第一层高度ymin=0.000 026 64,边界层厚度deta=0.011 91。

图1 RAE2822翼型网格Fig.1 RAE2822 grid configuration
1.2.2 算例验证
[16],来流条件取Case9对RAE2822翼型网格及计算方法有效性进行验证计算。参数经过修正后见表1。

表1 计算条件Table 1 Computational condition
图2为壁面压力系数的计算结果和试验结果对比图。试验数据参见文献[16],SA和SST数据为计算所得。可以看出计算对于激波位置和强度的捕捉都很准确。由于SA模型计算效率更高,后续计算中均采用SA模型。
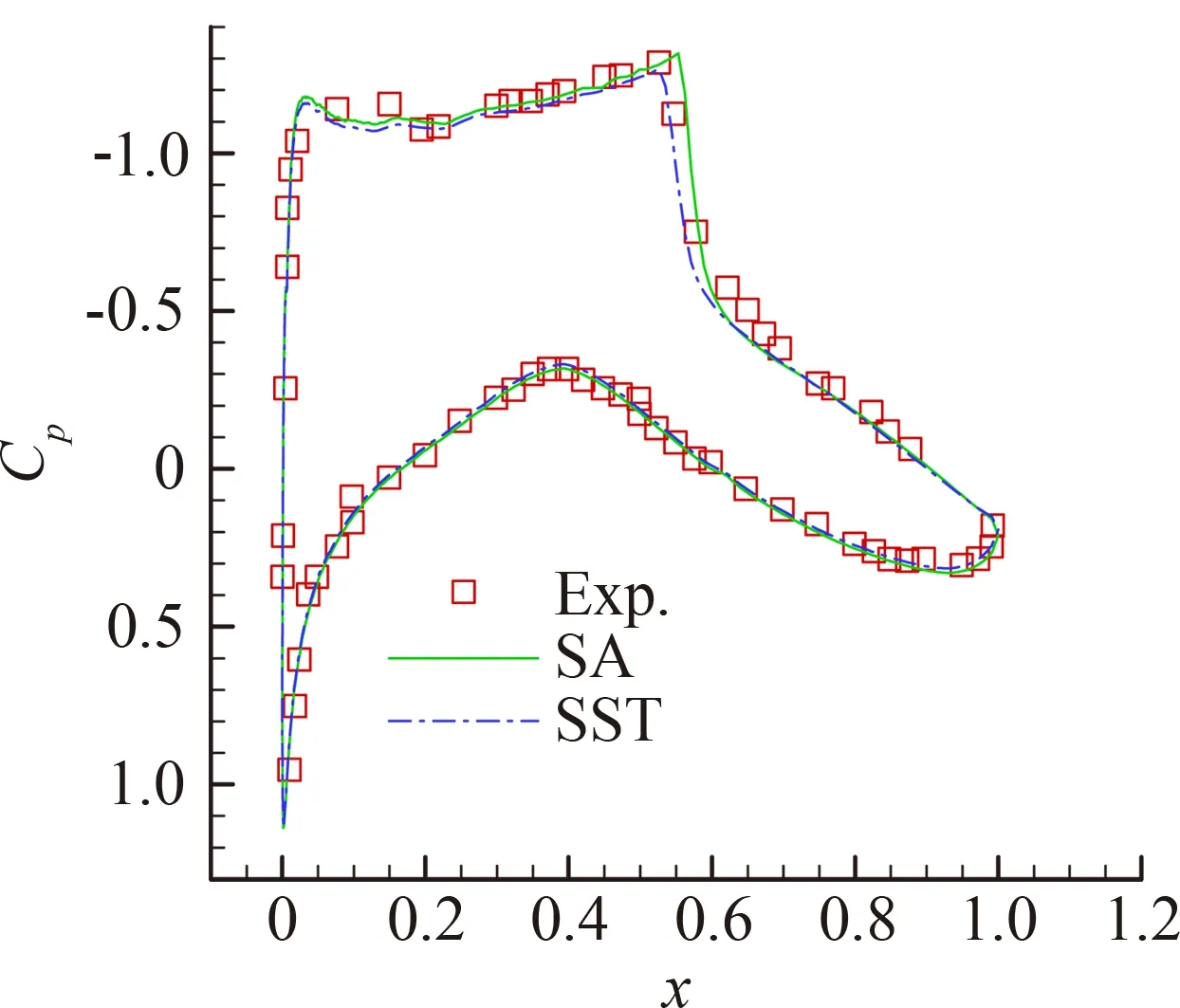
图2 本文计算壁面压力值与试验值的比较Fig.2 Comparison of pressure coefficient between calculated and test value
1.3 翼型变形方法及实现
为实现柔性变形,采用三角函数来实现往复变形过程。
1.3.1 变厚度方法
翼型厚度变形方式是将翼面所有控制点纵坐标在原有基础上等幅度增加。翼形表面控制点坐标变化方程为:
y=yinit[1+Asin(2πft)]
其中,yinit为翼面控制点初始坐标,A为厚度相对变化幅值,f为翼型变形频率。厚度相对变化量随时间变化关系如图3所示。

图3 厚度相对变化量随时间变化Fig.3 Relative change in thickness varies over time
1.3.2 变弯度方法
翼型的中线方程不易代数表达,故将弦线定义成一段抛物线。抛物线与x轴交点为翼型两端点,顶点纵坐标随时间正弦改变,并在瞬时弦线基础上加上原始翼型上下翼面的纵坐标。这样得到的变弯度翼型每个位置的厚度变化不大。变形公式如下:
P=Asin(2πft)
Δy=-4Px2+4Px
其中,P为顶点瞬时坐标,A为顶点变形幅值,f为变形频率,Δy是翼面控制点纵坐标的增加值。
为方便起见,采用变形后的弦线在(1,0)点处切线与横坐标夹角θ(单位:°)来衡量弯度大小。抛物线顶点在上时(图4)规定弯度度数为正,顶点在下时为负。弯度随时间变化关系见图5。
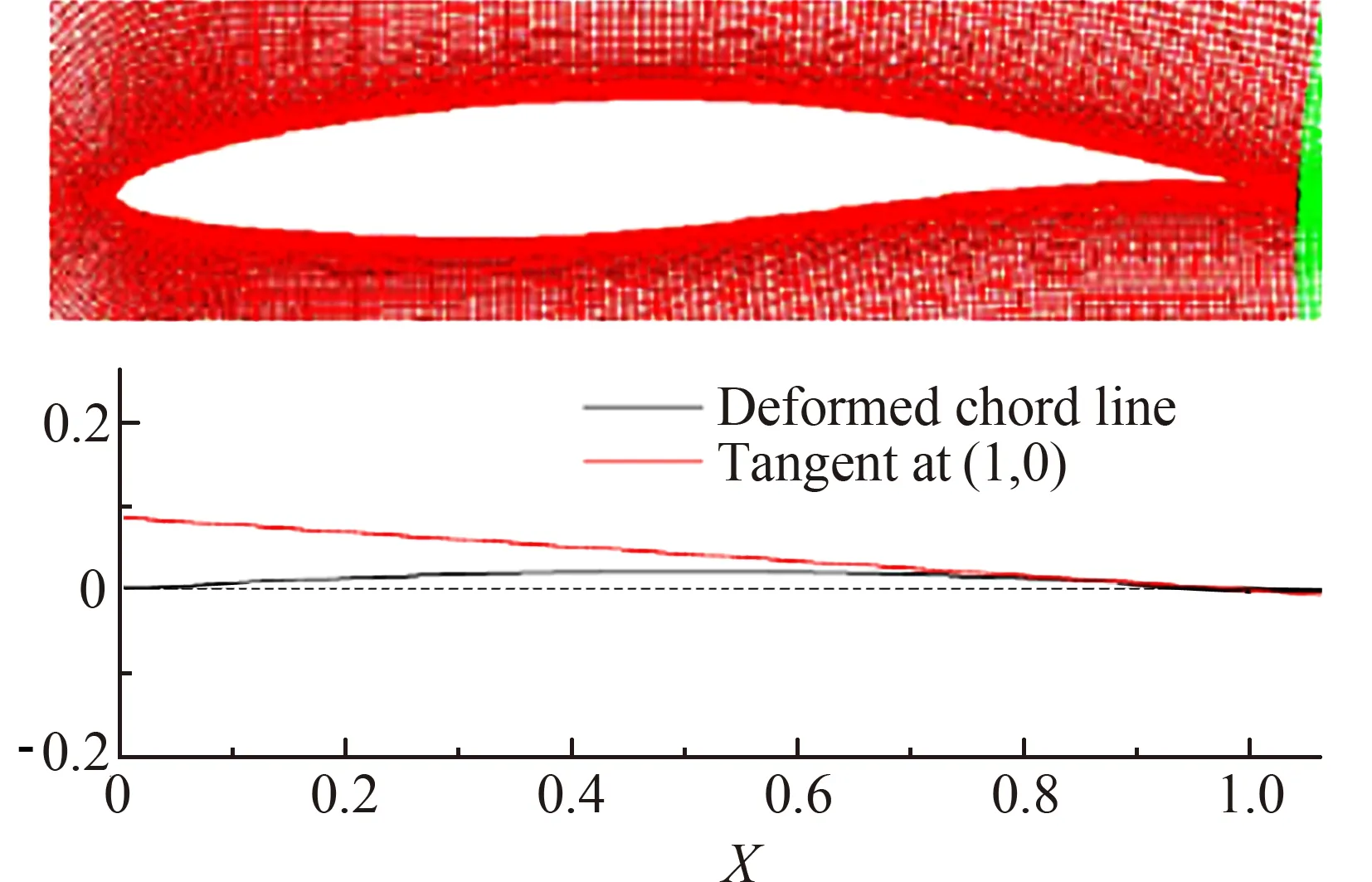
图4 θ=5°变形翼型Fig.4 θ=5° deformable airfoil
1.4 时间步长的选取
以厚度为例,在Ma=0.74、α=2°、相对变形幅值A=15%、变形周期f=1 Hz的情况下,分析内迭代步数取50步时,外时间步变化对升力系数计算结果的影响(图6)。结果表明外迭代步数取1000步时结果已收敛。故此类变形条件下外迭代步取1000,内迭代步取50。弯度及不同变形参数下的步长选取方法是一致的。
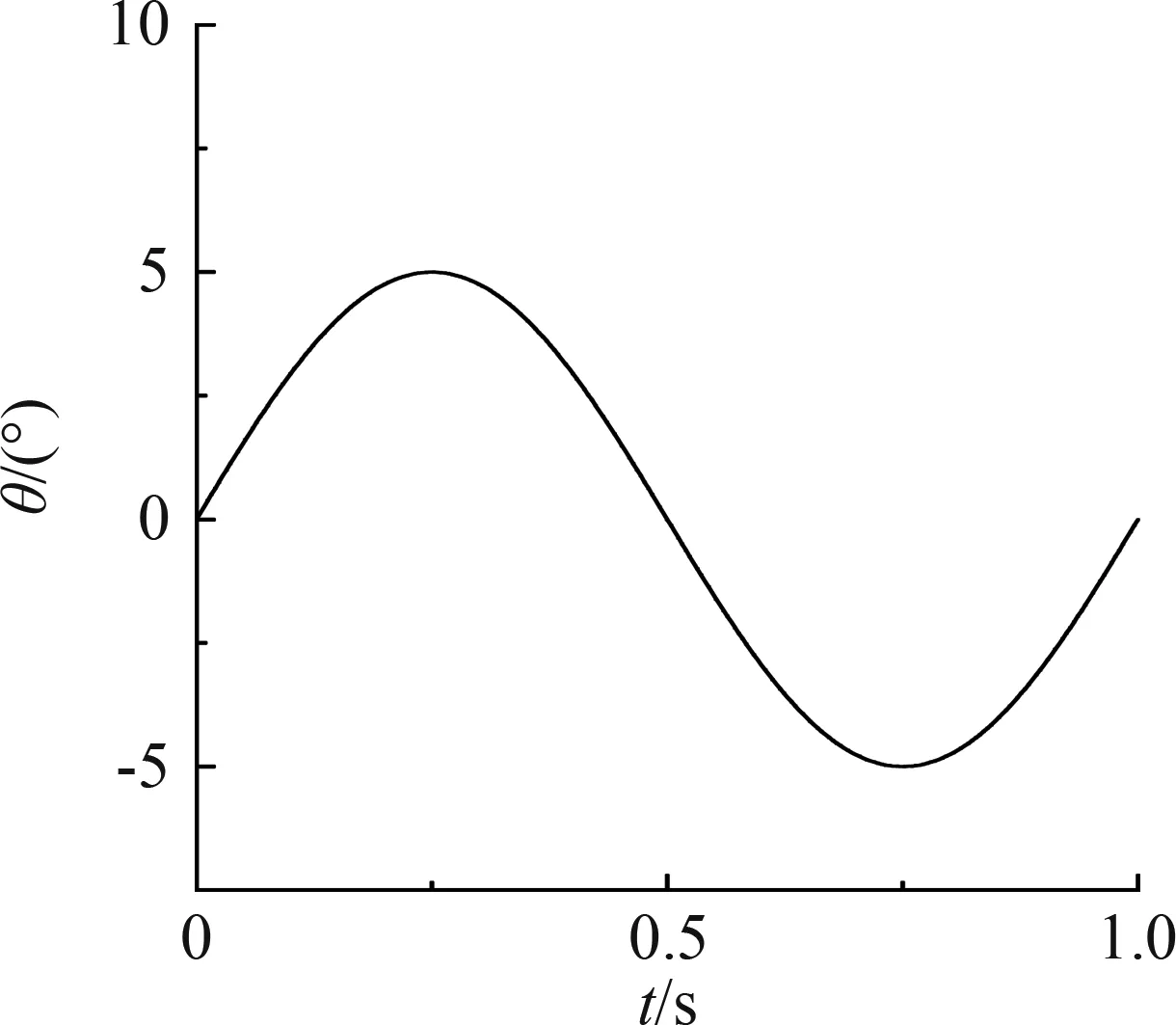
图5 弯度随时间变化Fig.5 Camber varies over time
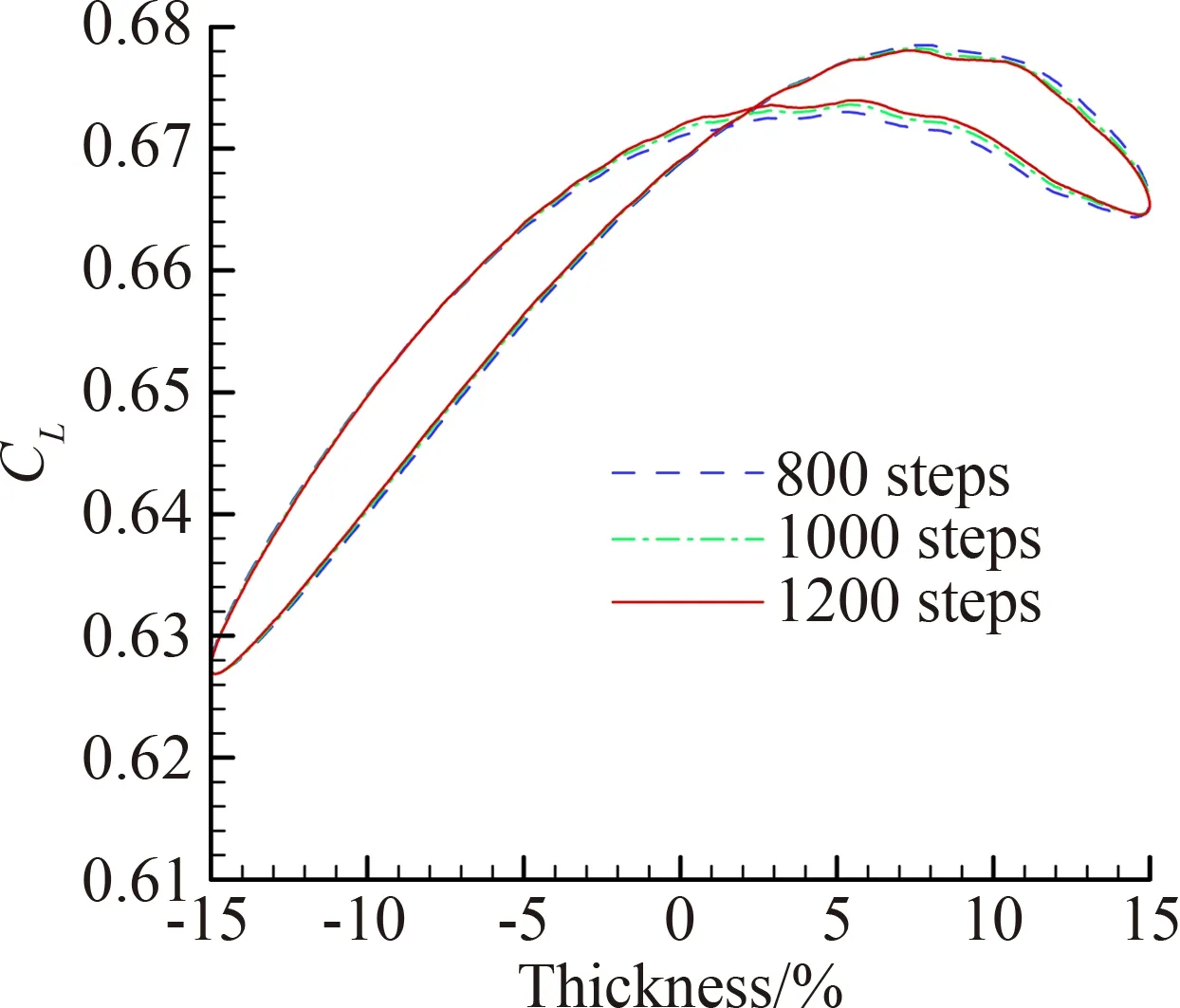
图6 不同外时间步下升力系数的比较Fig.6 Comparison of CL in different time step sizes
2 计算结果与分析
本文采用上述的数值方法,在Ma=0.74,α=2°条件下对RAE2822超临界翼型进行了数值模拟研究,主要考察了翼型厚度、弯度的变形幅度和变形频率对气动力的影响规律。
2.1 厚度变形对气动特性影响及分析
图7给出了Ma=0.74、α=2°,厚度相对变化分别为10%、15%、20%三种幅值下的气动力变化规律。由图可知,随着厚度变形幅值的增大,迟滞现象愈加明显。升力系数所形成迟滞环的面积,可以理解为机翼变形过程中外界所需输入的功,面积越大所需功越大[17]。图8给出了变形幅值为15%时,0.5 Hz、1 Hz、2 Hz三种变形频率的影响结果。由图可知,变形频率越高,升/阻力系数迟滞环面积越大。这表明厚度变形频率越快,其流场速度势随时间变化率所引起的非定常附加升、阻力系数也越大[17]。
总体来看,在一定幅值和频率范围内,往复变形经过同一位置时升力系数差别可达0.015,阻力系数差别可达0.001 9。

(a) 升力系数
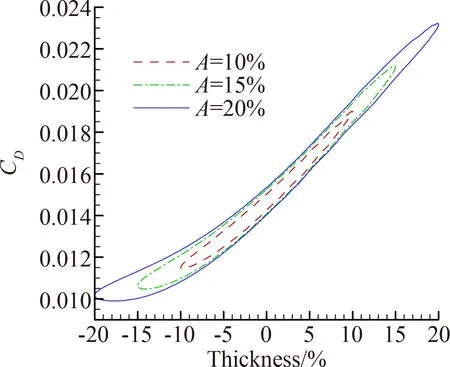
(b) 阻力系数
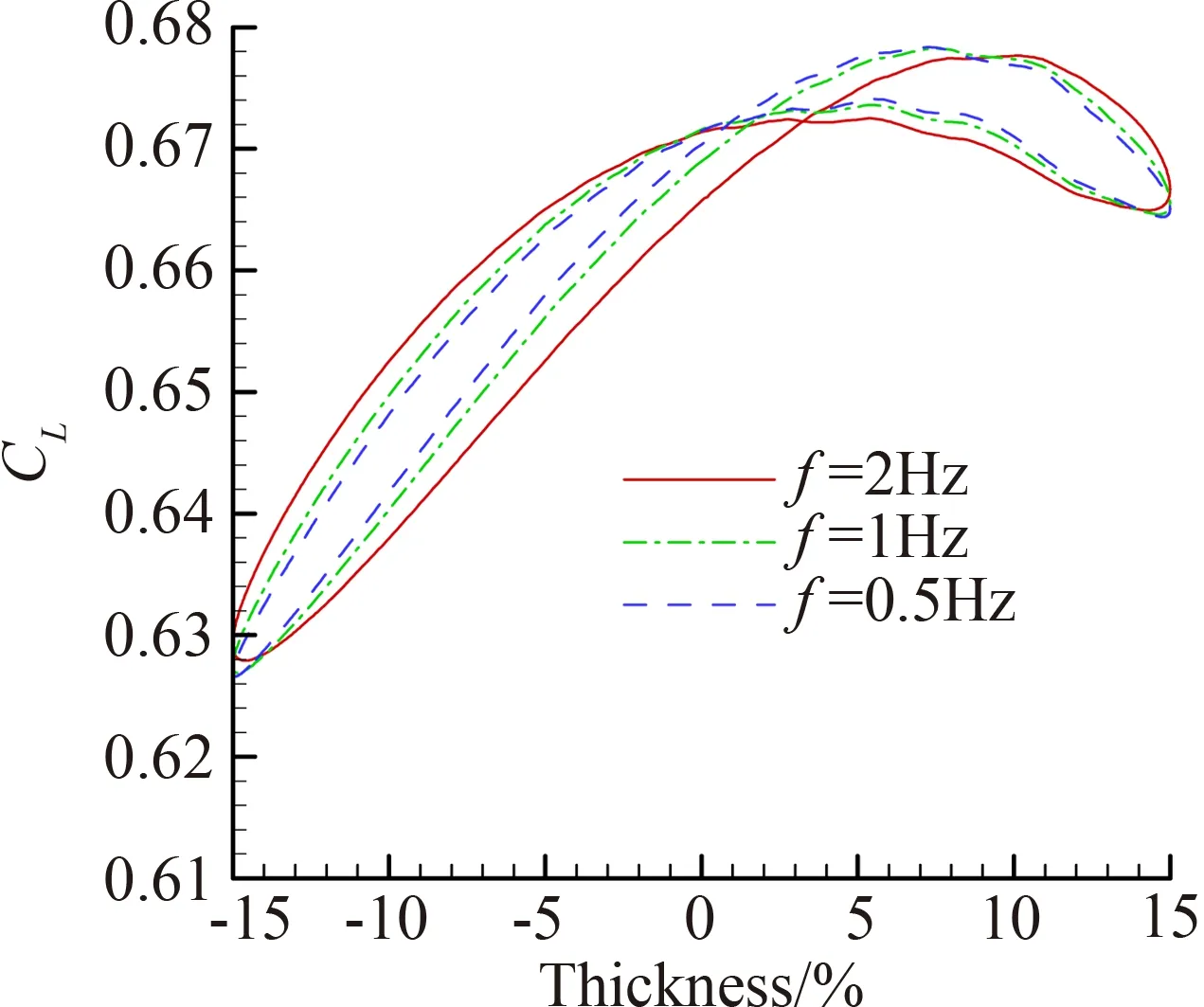
(a) 升力系数
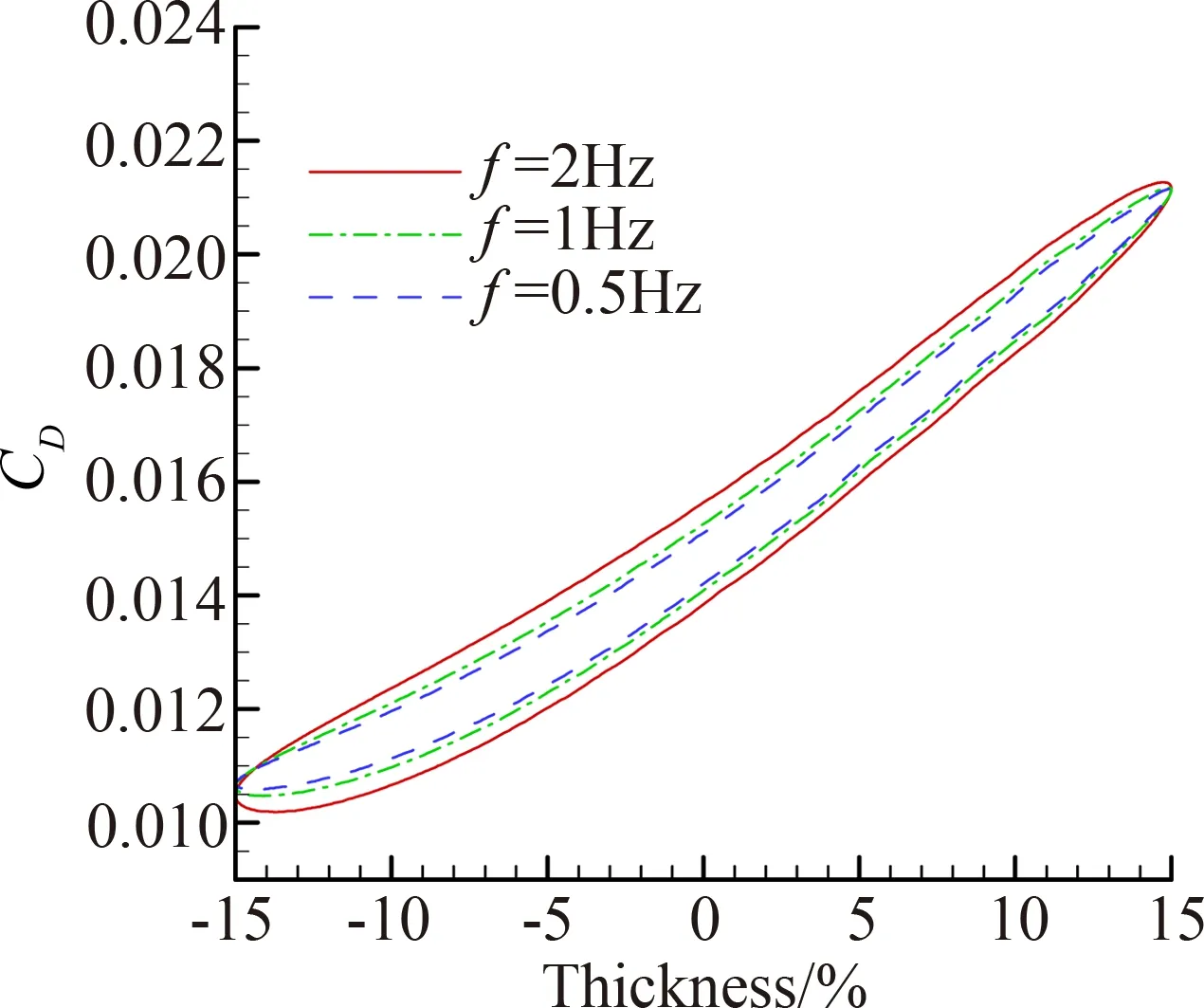
(b) 阻力系数
2.2 弯度变形对气动特性影响及分析
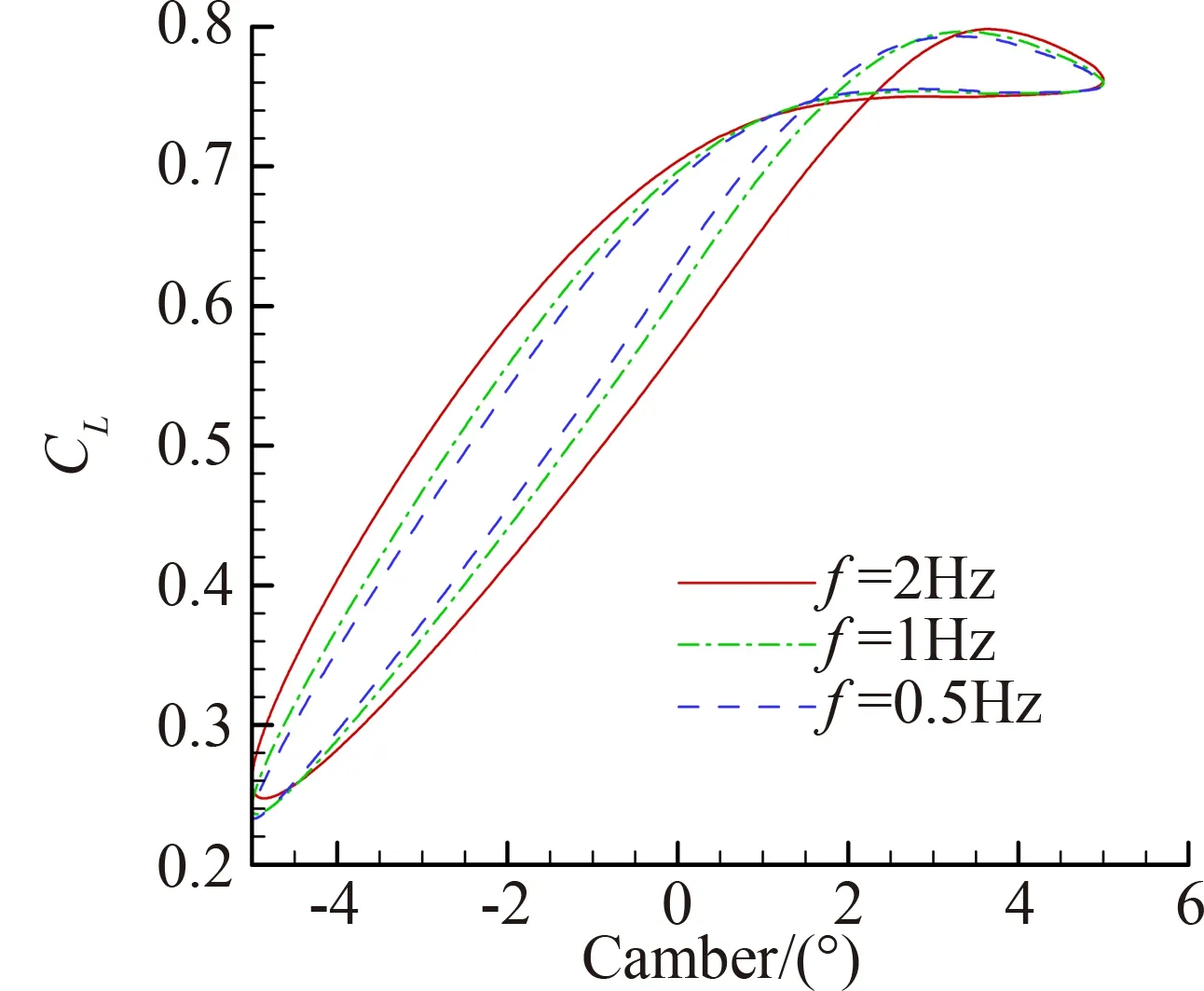
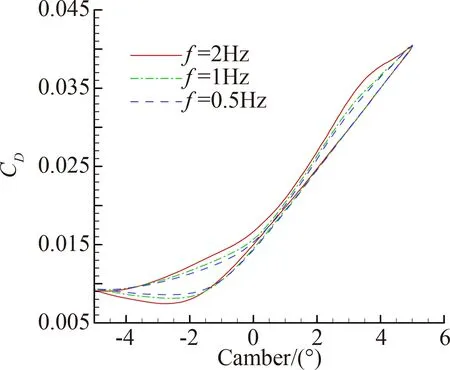
图9给出了Ma=0.74、α=2°,1°、2°、5°三种弯度变形幅值下的升/阻力系数变化规律。图中“θ=5°”代表弯度变形幅值为5°。由图可知,变形幅值越大,非定常效应越强,具体表现为迟滞环面积越大。相比于厚度变形,在一定幅值范围内弯度变形引起的非定常附加气动力更大,往复变形经过同一位置时升力系数差别可达0.117,阻力系数差别可达0.003 4,非定常效应更不容忽视。
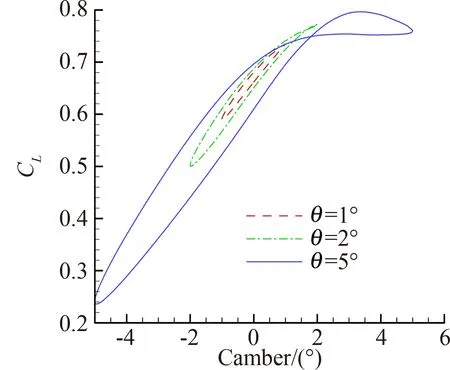
(a) 升力系数

(b) 阻力系数
图10给出了变形幅值为5°时,弯度变形频率对翼型气动特性的影响。由图可知,弯度变形频率越高,迟滞环面积越大。流场速度势[17]随时间变化率所引起的非定常附加升力系数也越大。
以上研究表明翼型厚度及弯度变化均会带来流动非定常性,表现在气动力系数具有明显迟滞特性。同时翼型几何参数变形幅值越大、变形频率越高,流动的非定常效应越强。与厚度变形影响相比,在上述条件下翼型弯度变形引起的非定常附加气动力更大,非定常效应更强。
2.3 非定常现象流动机理
Ma=0.74,α=2°,弯度变形幅值为5°,f=1 Hz,考察往复变形经过θ=3.5°时翼型压力分布变化情况(图11)。结果表明,第二次经过这个弯度时激波位置更加靠前,这是由于激波强度和位置相对于几何变形的迟滞造成的。
(a) 升力系数
(b) 阻力系数
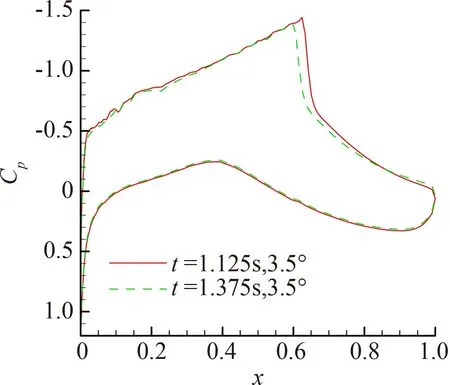
图11 往复变形经过3.5°时的Cp对比图(α=2°)Fig.11 Cp contrast diagram of reciprocating deformation after 3.5° (α=2°)
考虑另一情形:α=6°,其它变形参数与α=2°时一样。此时翼型的分离现象已经很严重。图12给出了同一周期往复变形两次经过θ=-3°时的流线图,可以看出第二次经过-3°时比第一次经过-3°时分离点位置前移。
图13给出了α=2°时弯度变形幅值和变形频率对压力分布的影响。结果显示,弯度变形幅值越大、变形频率越高,翼型两次经过同一弯度时的压力分布变化幅度越大,如激波强度大幅增强,激波位置后移幅度更大而使得压力系数曲线所包围的面积更大,即非定常附加升力系数更大。
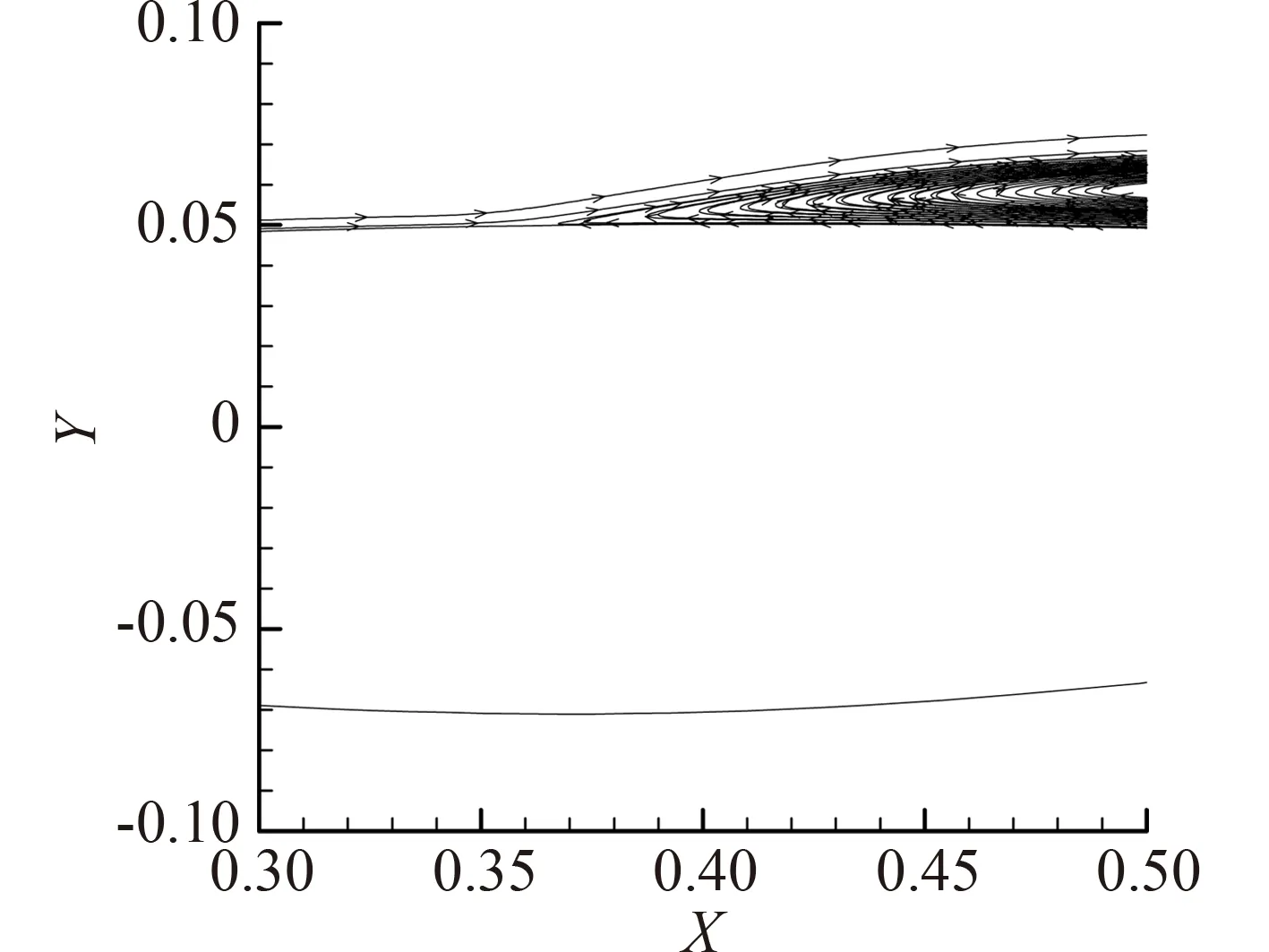
(a) t=1.6s

(b) t=1.9s
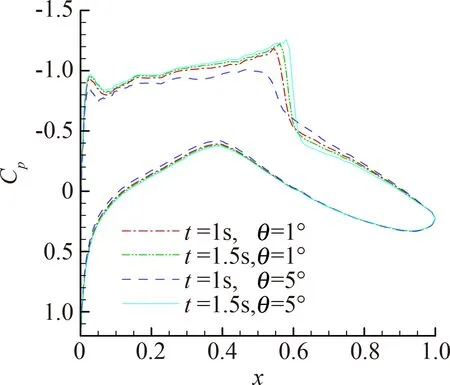
(a) 变形幅值对压力分布影响(f=1 Hz)
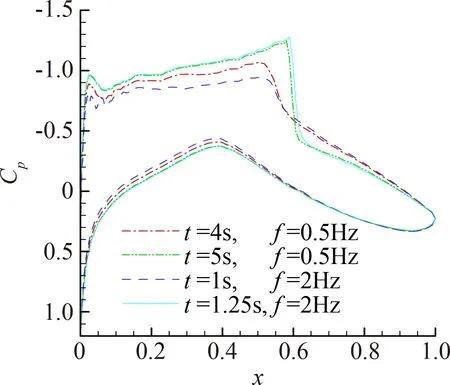
(b) 变形频率对压力分布影响(幅值5°)
通过研究发现激波位置、强度及附面层分离等流动结构随几何变形的迟滞性会导致非定常效应的产生,这与文献[18]的分析是相吻合的。
3 结 论
本文重点研究了超临界翼型RAE2822厚度及弯度柔性变形时幅值和频率对非定常效应强弱的影响,并初步分析了非定常效应产生的流动机理,通过研究发现:
1) 翼型厚度、弯度变化会引起流动非定常性,表现在气动力系数具有明显迟滞特性,形成明显的升、阻力系数迟滞环。表明在工程设计中需要对翼型变形过程中的非定常气动特性予以重视。
2) 翼型几何参数变形幅值越大、变形频率越高,流动的迟滞特性越明显,非定常效应越强。与厚度变形影响相比,翼型弯度变形带来的非定常效应更不可忽视。
3) 这种非定常效应源自激波位置、强度和附面层分离特性对几何变形的迟滞响应,以及由此导致的非定常附加气动力。
参 考 文 献:
[1]Secanell M, Suleman A, Gamboa P. Design of a morphing airfoil for a light unmanned aerial vehicle using high-fidelity aerodynamic shape optimization[C]//Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, 2005. Austin, TX, United States: American Inst. Aeronautics and Astronautics Inc.
[2]Cui Erjie, Bai peng, Yang Jiming. Development road of smart morphing aircraft[J]. Aeronautical Manufacturing Technology, 2007, (8): 38-41. (in Chinese)崔尔杰, 白鹏, 杨基明. 智能变形飞行器的发展道路[J]. 航空制造技术, 2007, (8): 38-41.
[3]Florance J P, Burner A W, Fleming G A, et al. Contributions of the NASA Langley research center to the DARPA/AFRL/NASA/Northrop Grumman smart wing program[C]//Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2003. Norfolk, VA, United states: American Inst. Aeronautics and Astronautics Inc.
[4]Kudva J N, Martin C A, Scherer L B, et al. Overview of the DARPA/AFRL/NASA Smart Wing Program[C]//Proceedings of SPIE Conference on Industrial and Commercial Applications of Smart Structures Technologies, 1999: 230.
[5]Kudva J N. Overview of the DARPA smart wing project[J]. Journal of Intelligent Material Systems and Structures, 2004, 15(4): 261-267.
[6]Ajaj R M, Beaverstock C S, Friswell M I. Morphing aircraft:The need for a new design philosophy[J]. Aerospace Science and Technology, 2016, 49: 154-166.
[7]Nekoubin N, Nobari M R H. Numerical investigation of transonic flow over deformable airfoil with plunging motion[J]. Applied Mathematics and Mechanics, 2015, 37(1): 75-96.
[8]Walker W P, Patil M J. Unsteady aerodynamics of deformable thin airfoils[J]. Journal of Aircraft, 2014, 51(6): 1673-80.
[9]Gandhi F, Anusonti-Inthra P. Skin design studies for variable camber morphing airfoils[J]. Smart Materials and Structures, 2008, 17(1): 015025. [10]Andersen P B, Gaunaa M, Bak C, et al. A dynamic stall model for airfoils with deformable trailing edges[J]. Journal of Physics: Conference Series, 2007, 75: 012028.
[11]Xu Guowu, Bai Peng, Shi Wen. Primary research of morphing scheme over 2D airfoil[J]. Chinese Quarterly of Mechanics, 2011, (4): 570-576. (in Chinese)徐国武, 白鹏, 石文. 二维翼型可变形方案初步研究[J]. 力学季刊, 2011, (4): 570-6.
[12]Hao Nansong, Yang Wenchao, Yang Jiming. Experimental study of unsteady aerodynamic characteristics of variable camber wing at low Reynolds number[J]. Journal of Experimental Mechanics, 2014, (3): 294-301. (in Chinese)郝南松, 杨文超, 杨基明. 低Re数下变弯度机翼的非定常气动特性实验研究[J]. 实验力学, 2014, (3): 294-301.
[13]Chen Qian, Bai Peng, Li Feng. Morphing aircraft wing variable-sweep: two practical methods and their aerodynamic characteristics[J]. Acta Aerodynamica Sinica, 2012, 30(5): 658-663. (in Chinese)陈钱, 白鹏, 李锋. 可变形飞行器机翼两种变后掠方式及其气动特性机理[J]. 空气动力学学报, 2012, 30(5): 658-63.
[14]Gao Yanfeng, Liu Zhifan, Wang Xiaohong. Study on the supersonic unsteady aerodynamic force for the morphing airfoil[J]. Acta Aerodynamica Sinica, 2014, 32(1): 69-76. (in Chinese)高彦峰, 刘志帆, 王晓宏. 可变形翼型超声速非定常气动力的研究[J]. 空气动力学学报, 2014, 32(1): 69-76.
[15]Gao Yanfeng, Wang Xiaohong, Liu Zhifan. Study on the subsonic unsteady aerodynamic force for the morphing joukowski airfoil[J]. Chinese Quarterly of Mechanics, 2012, (1): 1-9. (in Chinese)高彦峰, 王晓宏, 刘志帆. 可变形儒可夫斯基翼型亚音速非定常气动力的研究[J]. 力学季刊, 2012, (1): 1-9.
[16]Zhang Yifan, Zhang Xiaoli. Credibility analysis of RAE2822 airfoil transonic flow computation[J]. Aeronautical Computing Technique, 2009, (4): 68-70. (in Chinese)张一帆, 张小莉. RAE2822翼型跨音速流动CFD计算的可信度分析[J]. 航空计算技术, 2009, (4): 68-70.
[17]Gao Yanfeng. Study on the unsteady aerodynamics characteristics for the morphing airfoil[D]. University of Science and Technology of China, 2012. (in Chinese)高彦峰. 可变形翼型的非定常气动特性研究[D]. 中国科学技术大学, 2012.
[18]Yang Wenchao. Experimental investigation on the flow separation behaviors of a variable camber wing[D]. University of Science and Technology of China, 2012. (in Chinese)杨文超. 可变弯度机翼流动分离特性的实验研究[D]. 中国科学技术大学, 2012.
Unsteady aerodynamic characteristics of deformable supercritical airfoil
Shi Wenkui, Wang Yuanjing*, Zhang Zhao
(ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China)
People hope that aircraft shape can adjust according to the change of flow condition, thus it is essential to learn about the unsteady aerodynamic phenomenon and mechanism of deformable aircrafts. Then the deformation vehicle performance can be improved, and the safety of flight can be ensured. In this paper, supercritical airfoil was focused on, and airfoil thickness and camber deformation schemes were designed, respectively. Numerical simulation method was used to simulate the unsteady effect due to the airfoil thickness or camber deformed in high Reynolds number condition. The results show that the unsteady effect is strong with distinguishable lift and drag hysteresis loops. In addition, as the deformation frequency and amplitude increase, the unsteady effects are significantly strengthened. The unsteady effect resulted from the camber deformation is relatively stronger than that from the thickness deformation. Finally, by analysing the flow streamline and pressure coefficient distribution, the unsteady effects with geometric distortion can be produced by the hysteresis of the flow structure, such as the strength and location of shock, and the boundary layer separation.
supercritical airfoil; morphing wing; unsteady effects; aerodynamic characteristics; flow structures
0258-1825(2017)02-0192-06
2016-09-15;
2016-12-10
试验技术青年基金
施文奎(1993-),男,研究实习员,研究方向:光滑粒子流体动力学. E-mail: helloswk@126.com
王元靖*,男,副研究员,E-mail: 15209307@qq.com
施文奎, 王元靖, 张兆. 变形体超临界翼型动态气动特性[J]. 空气动力学学报, 2017, 35(2): 192-197.
10.7638/kqdlxxb-2016.0110 Shi W K, Wang Y J, Zhang Z. Unsteady aerodynamic characteristics of deformable supercritical airfoil[J]. Acta Aerodynamica Sinica, 2017, 35(2): 192-197.
V211.3
A doi: 10.7638/kqdlxxb-2016.0110
