有关近空间高超声速飞行器边界层转捩和湍流的两个问题

周 恒, 张涵信

(1.天津大学 力学系, 天津 300072; 2. 中国空气动力研究与发展中心 国家计算流体力学实验室, 北京 100191)



有关近空间高超声速飞行器边界层转捩和湍流的两个问题

周 恒1,*, 张涵信2

(1.天津大学 力学系, 天津 300072; 2. 中国空气动力研究与发展中心 国家计算流体力学实验室, 北京 100191)

和一般的飞行器一样，在近空间飞行器的研制中，其边界层的转捩和湍流也是需要考虑的两个重要问题。但即使是对一般的飞行器，“转捩”和“湍流”也还是两个历经百年而仍未很好解决的问题，而对近空间飞行器来说，空气动力学本身就还存在若干新的需要研究解决的基础问题，边界层的转捩和湍流就更是没有很好解决的问题。本文讨论了两个问题：1) 为增强对高超声速飞行器边界层转捩预测的能力，需要开展哪些方面的研究工作及其困难；2) 是否有可能当飞行器飞行高度足够大时，其边界层就不会再有湍流问题?

近空间飞行器；转捩；湍流；预测能力

1 转捩预测问题

转捩问题历经百年的研究，在低速流方面已经有了不小的进展。而对高超声速边界层的转捩问题，近年来的研究虽有一些进展，但仍存在严重的不足[1-2]。

可以肯定，整个转捩过程可分为三个阶段或作为三个问题来研究。1) 感受性问题，即边界层外的扰动如何引发边界层内以不稳定波形式出现的扰动？2) 被引发的不稳定波在边界层内的演化。如果开始时幅值很小，例如一般认为，如果不稳定波的速度的幅值小于边界层外缘速度的1%，则可以用线性理论；而大于1%，则要用非线性理论。3) 扰动演化到什么情况将触发转捩？即预测转捩发生的判据。

以上的第二个问题研究的时间最长也最充分。特别是现在有了计算机和各种计算方法，只要知道扰动的初始条件，已经没有原则上的困难了。

第三个问题原来是一个难题。长期以来人们提出多种边界层内扰动演化的非线性理论，但始终无法和第三个问题，即演化到什么程度将触发转捩，联系起来。在文献[2]中，作者通过多种转捩的直接数值模拟，发现了转捩过程的机理是：扰动通过非线性作用对平均流进行修正，使得平均流剖面的线性稳定性发生变化。如果修正的结果是线性不稳定的参数区(例如线性稳定性理论的中性曲线所包含的区域)扩大，则会形成不稳定性的正反馈，从而触发转捩。他们并总结出，在技术人员喜欢用的半经验转捩预测方法eN法中，当不稳定波幅值达到1.5%时转捩将发生。这可以认为第三个问题在一定程度上已经解决。

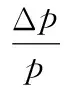
现今已有不少作者从事这方面的计算研究工作，例如Zhong等采用激波装配法[4-9]，Balakurma等则采用了激波捕捉法[10-11]，然而他们对激波捕捉法的正确使用和激波后的扰动的非定常分析均存在缺陷。有文给出了线性扰动解，还用平行流假定作声波、熵波和涡波分析，对高超声速绕流这都是欠适当的。对有复杂激波系的问题，用激波装配法来研究扰动通过激波经历的变化是不现实的，而用激波捕捉法是否能可靠地反映这一变化则有待于新的能证实其可靠性的研究结果。

因此，为了解决转捩预测问题，当前最需要做的基础研究就是超声速/高超声速条件下的感受性问题。

前文已述，解决感受性问题的一个拦路虎就是飞行环境下的扰动是什么不清楚，为此就要做实地测量的飞行试验。

从Zhong等已有的直接数值模拟结果来看，激波后的声波在感受性问题中起主要作用，而激波前的声波又在产生激波后的声波中起主要作用。但在流体中，声波的产生只有三种来源：一是由流体中的外来物体的体积周期性变化所引起；二是由外来物体对流体的周期性作用力所引起；三是由流体本身的运动产生了周期性的雷诺应力所引起。而在高空，实际上不存在外来物体(不算飞行器本身)，因此可以认为不存在前两种声源。但第三种声源激发声波的效率很低，可以忽略不计。所以，飞行试验的目标就是测出大气中的以速度和温度扰动出现的涡波和熵波。

但这是非常困难的任务。首先，如果用超声速/高超声速飞行器作为仪器载体，则仪器只能感受飞行器头激波后的扰动。要还原成大气中原来的扰动，是要解一个反问题，而反问题的解是不唯一的。其次，仪器的传感器要有非常高的灵敏度。例如，一般估计对马赫数为20的飞行器，速度背景扰动的幅值为万分之一的量级。而如果马赫数为6时，同样的扰动对应的无量纲幅值就是万分之三的量级。因此，测量时仪器就要有能分辨速度的万分之一或万分之三的变化的能力。而频率范围则要高达几十万赫兹，对温度传感器的要求也类似。如果要用亚声速的飞行器作为仪器载体，则对仪器传感器的灵敏度和频响范围的要求低得多，但如何将该飞行器送上高空后能有一段亚声速的平飞段是一难题，而且亚声速的飞行器本身对大气流动的干扰会反映到传感器上，如何排除？有人认为在30 km以下似乎可以用探空气球作为仪器载体。但探空气球的存在改变了周围相当大的一片区域的流场，仪器的传感器能否伸出到离气球足够远的地方？

通常，在飞行器的设计中，地面的风洞实验起了很大的作用，但要将地面风洞作为工程问题的转捩预测的手段，是不够的。如前所述，人们早就认识到对超声速流而言，小扰动可分解为三种扰动。风洞的实验段收缩比加大后，三种扰动更小，于是就认为风洞气流几乎没有声、熵、涡扰动。这在最初只是从减小背景扰动幅值的结果来考虑的。但现在知道，从感受性的角度看，声波扰动、涡波扰动及熵波扰动的作用是不同的。同样幅值的声波和涡波导致的转捩结果是不同的[3]。而上面的讨论中已提到，高空大气中本质上不存在声波。而静风洞的出现则在不自觉的条件下正好满足了这一要求(静风洞的出现比文献[3]中所纪录的声波扰动和涡波扰动导致的小钝头锥上的转捩线定性上就不同的研究结果要早得多)。但如果要模拟真实的转捩，则静风洞中的剩余扰动必须和真实情况下的背景扰动一致(无量纲化后一致)，而我们实际上并不知道实际扰动是什么(如上所述，需要由飞行试验测定)。而且即使知道了，要在风洞中实现(至少是对转捩起作用的扰动频率段的谱要一致)也是很大的难题。

此外，还有其他问题使得现有的风洞不能完全满足预测工程问题中的转捩的要求。这是因为：1)N-S方程无量纲化后，和不可压缩流的情况不同，方程的系数并不是常数，而还有无量纲化后的粘性系数和普朗特数。粘性系数和温度有关，而且对高超声速流来说，实际飞行中边界层的温度还可能很高，从而粘性系数还要受气体分子内能被激发、离解、甚至化学反应的影响。因此，要做到模型和实际飞行器的无量纲方程中的粘性系数一致，只有二者的温度场完全一致才行，而这在现有的风洞中是不可能做到的。2)模型和实际飞行器的表面温度还要一致，因为边界层内的不稳定波的演化受温度边界条件的影响是很大的，而这一项的要求显然也不可能在实验中实现。因此，做到风洞试验和工程实际的完全相似目前是做不到的。

既然这样，那风洞实验还能起什么作用呢？我们认为，目前它能起的最大作用是能提供有较完备参数的实验结果，可以作为检验转捩预测方法的依据。即将转捩预测方法先直接面对风洞和模型的参数，而不是针对实际飞行器的参数，以检验其预测转捩的结果是否和风洞实验结果相符。但这样做，就要求给出风洞实验段的背景扰动的频率谱及模型壁面温度(不是实验开始前的温度，而是实验过程中的温度)分布。

2 湍流问题

迄今为止，在近空间以高超声速飞行的飞行器是否必须考虑湍流问题还没有一个可靠的说法。实际飞行实验的结果非常少。经常被引用的只有几篇文章，都还是20世纪七、八十年代的。文献[12]是关于一个长近4 m、半锥角为5°的小钝头锥，从约100 km高空返回地面的过程中做的试验。从100 km高空到约13 km高空，其飞行马赫数都在20左右。结果发现一直降到30 km左右，才开始在尾部出现湍流。随着高度不断降低，转捩线往前移，即湍流区不断扩大。文献[13]是1974年发表的，研究对象为长67.23 cm、鼻锥半径16.09 cm、底部直径48.69 cm的9°鼻锥。由拖曳火箭把它送上天，以5 km/s、迎角12.5°再入飞行，锥面有泰氟隆涂层，实验结果用粗糙度稍大的转捩准则处理。当飞行高度是36.58 km以上，气流全为层流；30.48 km时，湍流区已扩展至鼻端，即高度为36.58 km以下会有湍流的影响。文献[14]也有类似的结果。后来美国根据自由飞和风洞实验结果，提出了不同粗糙度转捩准则的转捩公式[15]。我们要求近空间飞行器和航天飞行器一样，基本上是光滑的，即实际粗糙度比上述实验的粗糙度小，则可以合理地认为，开始发生转捩的高度至少应在40 km到45 km间。2015年又有几篇有关美国HIFiRE-1计划的分析试验报告，但其飞行高度值仅达到稍高于25 km。

型号设计中总提出一个问题：什么高度就可以不考虑湍流和转捩影响，特别是近空间滑翔飞行器?从上面的分析来看，似乎可以认为飞行高度在45km以上就可以不考虑转捩和湍流问题，但实际上问题也许不是这么简单。

首先，为了验证我们的结论，我们努力收集了国外飞行器的飞行结果，包括双子星座、Apollo、美国各种航天飞机、苏联的飞船、英国的Hermes航天器、日本的小型飞船、美国的HTV-2以及中国的飞船，特别是哥伦比亚失事调查、复飞以及HTV-2前部的破坏等，都没有发现是因为在40～50 km以上没有考虑转捩和湍流所导致的。最近美国正在改造世界最大的高超声速风洞(九号)，其一个重要目的是能够做边界层自然转捩的实验，他们把对应的飞行高度上限定为50 km。 以上是从已有的实际情况总结出来的结论，或许我们也可以从另一个角度对此问题做一些分析，即从气体稀薄程度来判断是否会有湍流。

本文作者曾在另一篇文章中[16]指出，对不同的问题，判断是否要考虑气体的稀薄效应要用不同的标准，否则按早年的观点，高度在80 km以下的范围，对飞行器的设计来说，都可以用连续介质模型。2005年黄章峰等在他们的一篇文章[17]中，报告了他们所做的一个在30 km高空、以马赫数4.5飞行的平板边界层的湍流直接数值模拟。结果发现，所得到的湍流和低速边界层的湍流有几乎完全相同的特征。例如，在壁面区存在低速条纹，其间距约为100个粘性长度，此间距会随离壁面的距离增加而逐渐加大。在湍流近壁区，存在相干结构，其特征也和低速边界层中的湍流相似。因此，我们可以假定在近壁区出现低速条纹，且条纹间距约为100粘性长度，是湍流边界层的普适现象。在判断是否有湍流问题时，判断气体稀薄与否的参考长度也许就应取这一长度。

我们也可以先假定连续介质模型可用，对在更高空处飞行的平板做类似的计算，但要计算多种工况则工作量较大，而采用以下的从层流解来估计则要方便得多。

设在某一高度有一平板以0°迎角及某一速度飞行，则可按相似性解得到层流边界层的解，从而得到相应的粘性长度。

例如，对位于10 000 m和30 000 m高空的平板层流边界层，采用相似性解，得到马赫数为0.85和4时，位于离前缘2 m处的粘性长度l+见表1。

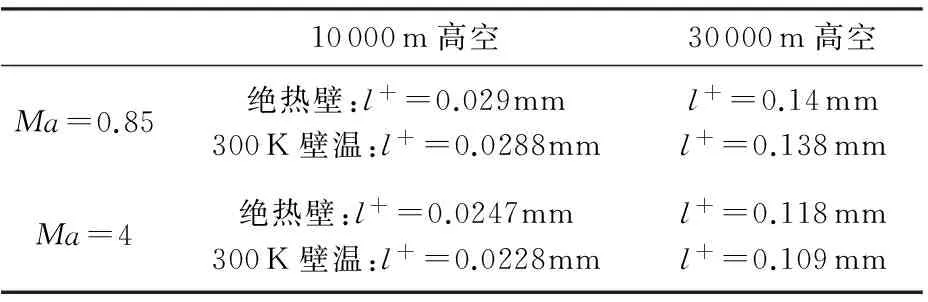
表1 不同高空、不同马赫数下的粘性长度Table 1 Viscous length at different altitude and different Mach number

由以上结果看，马赫数和壁面的温度条件对粘性长度的影响不大，而高度则影响较大。高度从10 000 m增至30 000 m，l+就增加为原来的约4.8倍。

黄章峰的DNS显示，从层流转捩为湍流时，壁面摩擦系数增为原来的3～4倍。其他人对不可压边界层做的转捩直接数值模拟，也得到类似的结果。如果取3，则对应于湍流边界层，粘性长度单位约相当于层流的(1/3)1/2≈0.58倍。因此，对湍流边界层来说，粘性长度和高度变化的规律也不变，在高度从10 000 m增加到30 000 m时，也是增为原来的4.8倍，或高度每增加10 000 m，粘性长度约增加约2.2倍。在比30 000 m更高的高空，这一增加的比例变化不会有量级的变化。

但是从10 000 m高空开始，高度只要每增加10 000 m，大气分子自由程就增为原来的约4.7倍。因此，高度每增加10 000 m，湍流边界层近壁区的低速条纹间距和当地分子自由程之比就要降为原来的约2.2/4.7=0.47倍。当这个比值降到一定的程度，低速条纹就无法维持了，即不会有湍流了。

10 000 m高空分子自由程约为0.22μ，30 000 m高空时约为4.7μ。对300 K壁温情况：马赫数为4时，在靠近壁面处，温度升高很少，当地分子自由程和来流的分子自由程基本相同。而相应地湍流边界层低速条纹间距(0.58×100l+)则分别约为1.322 mm和6.322 mm，间距和分子自由程之比分别为6009和1345。

如果马赫数达20，则对定温壁(300 K)，在层流边界层厚度的1/8处，温度约为来流温度的11倍[18](对湍流边界层应更高一些)。相应地，对30 000 m高空，该处的分子自由程可达52μ，或0.052 mm。一个低速条纹间距对应仅121个分子自由程。

按一般湍流研究结果看，湍流边界层近壁区的低速条纹是一种“大”结构，充分发展湍流中还应有比它尺度至少小一个量级的小结构。而要形成一个结构，其尺度又不能太小，必须包含足够多的分子，或者说，其尺度应该至少比分子自由程大一个量级。因此，低速条纹的间距至少应该比分子自由程大两个量级，或约100倍。否则，至少连续介质模型下的那种湍流是否能存在要存疑。但这也许还不能完全否定可能存在湍流。事实上，也许在一般的湍流和完全没有湍流之间存在一个过渡区，就像从层流到湍流存在一个转捩过程那样。在那个范围内，可能存在既非层流又非充分发展的湍流。

同样地分析，到40 000 m高空时，一个低速条纹仅对应约56个分子自由程。从物理上讲，应已不能形成通常意义下的湍流。

如果近空间飞行器采取的是耐高温材料防热，则壁面接近于绝热情况。马赫数为8时，壁面温度即可达来流温度的约11倍(层流相似性解)，即在40 km高空已不会有湍流。

由于长航程的高超声速飞行器一般都要飞行于较高的高度，例如至少是40 km或更高，飞行马赫数也较大，因此可能的确不需要考虑湍流和转捩的问题。

但是，不能无条件地应用这一结论。

实际上，前面的分析都是针对0°迎角飞行的平板而做的，其隐含的假定就是边界层内的压力和环境压力相同。对有迎角平板，情况就不一样了。

例如，假定平板以速度v，迎角θ飞行，则按牛顿理论，平板迎风面单位面积所受压力约为:

在海平面，空气单位重量约为1.29kg/m3，大气压约为10 339kg/m2。在30 km高空，空气单位重量和大气压力分别降为约0.0189kg/m3和119kg/m2。而在50 km高空，空气单位重量约为0.000 89kg/m3(以上数据不是精确值，因为高空的大气温度、密度和压力都是不断变动的)。如果马赫数为15，则其速度约为4500 m/s，代入式(1)，得

如果要求和30 km高空处大气压相当，即约为119kg/m2，则Sin2θ=0.0647，或θ=14.7°。即迎角达到14.7°时，其边界层内的压力就和在30 km高空以同样速度飞行但迎角为0°的平板一样，也就有可能发生转捩。

对于像锥体那样的飞行体，即使有迎角，在迎风面的压力升高显然远小于平板的情况，因此在飞行试验中未发现高度超过30 km时发生转捩也是可以理解的。但对有升力面的飞行器，则在升力面上，要根据实际边界层中的压力和温度，看边界层中的分子自由程和按连续介质模型所得湍流边界层中低速条纹间距(约100个粘性长度)相比的值。可以考虑暂时将这一临界值定为1%，大于它则多半不能维持湍流，也就不存在转捩问题了。

3 结束语

上面讨论了研制近空间飞行器需要研究考虑的两个空气动力学问题。给出了它们的研究现状，提出了为解决它们需要开展的研究及可能遇到的困难。由于问题的复杂，也由于已有的研究成果很少，因此提出的看法和建议不能说是完全正确的，也不能说是很全面的。随着研究的开展，可能还会发现新的问题，或者发现文中的观点不准确甚至不正确，这都是正常的。如果我们的观点或建议对今后的研究中能起到一定的促进作用，我们就很满意了。

[1]Berin J J, Cummings R M. Critical hypersonic aerothermodunamic phenomena[J]. Annual Review of Fluid Mechanics, 2006, 38: 129-157.

[2]周恒, 苏彩虹, 张永明. 超声速/高超声速边界层的转捩机理及预测[M]. 北京: 科学出版社, 2015: 1-49, 88-96.

[3]Pope A, Goin V L. High speed wind tunnel testing[M]. United Kingdom: Wiley, 1965.

[4]Zhong X. Leading-edgereceptivity to free-stream disturbance waves for hypersonic flow over aparabola[J]. Journal of Fluid Mechanics, 2001, 441: 315-367.

[5]Ma Y, Zhong X. Receptivity of asupersonic boundary layer overaflatplate. Part1. Waves tructures and interactions[J]. Journal of Fluid Mechanics, 2003, 488: 31-78.

[6]Ma Y, Zhong X. Receptivity of asupersonic boundary layer overaflatplate. Part2. Recep-tivity to free stream sound[J]. Journal of Fluid Mechanics, 2003, 488: 79-121.

[7]Ma Y, Zhong X. Receptivity of asupersonic boundary layer overaflatplate. Part3. Effects of different types of free-stream disturbances[J]. Journal of Fluid Mechanics, 2005, 532: 63-109.

[8]Ma Y, Zhong X. Boundary-layer receptivity of Mach 7.99 flow overabluntcone to free-stream acoustic waves[J]. Journal of Fluid Mechanics, 2006, 556(1): 55-103.

[9]Zhong X, Wang X. Directnumerical simulation on there ceptivity, instability and transition of hypersonic boundary layers[J]. Annual Review of Fluid Mechanics, 2012, 44(1): 527-561.

[10]Balakumar P. Receptivity of asupersonic boundary layer to acoustic disturbances[J]. AIAA J., 2009, 47(5): 1069-1078.

[11]Balakumar P, Kegerise M A. Receptivity of hypersonic boundary layers over straight and flared cones[J]. AIAA J., 2010, 53.

[12]Wright R L, Zoby E V. Flight measuement of boundary layer transition of a 50 half angle cone at free stream Mach number of 20 (reentry)[R]. NASA TM X-2253, 1971.

[13]Hayer D T, Herskovitz S B, Lennon J F, et al. An ablation technique for enhancing reentry antenna performance, flight test results[R]. FACRL-TR-74-0572, ADA012250, 1974.

[14]Hayer D T, Herskovitz S B, Lennon J F, et al. Flight test data comparing electron attachment by ablation products and by liquid injection. AIAA-75-181[R]. Reston: AIAA, 1975.

[15]Batt R Q, Legner H H. A review of roughness-induced nosetiptransition[J]. AIAA J., 1983, 21(1).

[16]周恒, 张涵信. 空气动力学的新问题[J]. 中国科学(中文版), 2015, 40(10): 104709.

[17]Huang Zhangfeng, Zhou Heng, Luo Jisheng. Direct numerical simulation of a supersonic turbulent boundary layer on a flat plate and its analysis[J]. Science in China G, 2005, 48(5): 626-640.

[18]Anderson J D Jr. Hypersonic and high-temperature gas dynamics[M]. Second Edition, AIAA Education Series, 2006, 293-296.

Two problems in the transition and turbulence for near space
hypersonic flying vehicles

Zhou Heng1,*, Zhang Hanxin2

(1.MechanicalSystemofTianjinUniversity,Tianjin300072,China;2.NationalLaboratoryforComputationalFluidDynamics,ChinaAerodynamicsResearchandDevelopmentCenter,Beijing100191,China)

For the research and development of near space flying vehicles, also as the same for conventional flying vehiclessuch as airplanes, the problems of transition and turbulence of the boundary layers are two important issues must be taken into consideration. However, even for conventional flying vehicles, these two problems are still not fully resolved, even though the investigations have been lasted for more than 100 years already. For near space flying vehicles, not only the related aerodynamics has its own unsolved fundamental scientific problems, let along the problems of transition and turbulence. In this paper, two related problems are focused on: 1) In order to enhance our capability of predicting the transition of the boundary layer of a hypersonic flying vehicle, what kinds of research work should we do and what difficulties we might face? 2) Would it be possible that there would be no problem of turbulence for its boundary layer if the attitude of the flying vehicle is sufficiently high?

near space flying vehicles; transition; turbulence; capability of predicting

0258-1825(2017)02-0151-05

2017-02-17;

2017-03-23

周恒*(1929-),男，中国科学院院士，研究方向：边界层转捩，流动稳定性非线性理论. E-mail: hzhou1@tju.edu.cn

周恒, 张涵信. 有关近空间高超声速飞行器边界层转捩和湍流的两个问题[J]. 空气动力学学报, 2017, 35(2): 151-155.

10.7638/kqdlxxb-2017.0016. Zhou H, Zhang H X. Two problems in the transition and turbulence for near space hypersonic flying vehicles[J]. Acta Aerodynamica Sinica, 2017, 35(2): 151-155.

V211.3

A doi: 10.7638/kqdlxxb-2017.0016