高分辨率超声Lamb波频散曲线测量与板厚估计*

2017-04-27许凯亮张正罡他得安

数据采集与处理 2017年2期

许凯亮张正罡刘丹他得安,3 胡波

(1. 巴黎第六大学、法国国家科学研究院、国家卫生与医学研究院生物医学成像实验室(LIB)，巴黎，75006，法国；2. 复旦大学电子工程系，上海，200433; 3. 上海市医学图像处理与计算机辅助手术重点实验室，上海，200032)

许凯亮1张正罡2刘丹2他得安2,3胡波2

超声Lamb波在工业无损检测与评价中具有广阔的应用前景。但受制于超声导波多模式频散与混叠的影响，如何实现高分辨率超声导波的模式分离与频散曲线提取，进而定量分析材料的健康状况一直是研究的热点与难点。本文旨在将现代信号处理中广泛采用的谱估计技术应用于超声Lamb波阵列信号分析，并通过提取频散曲线定量测量板厚度。以经典参数谱估计法中的Yule-Walker法与Burg法为例，实验测量和分析了3 mm,4 mm和 5 mm厚铝板中的宽带多模式Lamb波信号，准确地提取了铝板中的宽带Lamb波频散曲线，并比较了两种经典谱估计方法与二维傅氏变换法的性能，最终实现了铝板厚度估计。

超声Lamb波；经典谱估计法；频散曲线；厚度估计；无损检测

引言

超声导波技术在大规模工业无损检测与评价的应用中已经展现出巨大潜力[1]。它能被应用于输油管道、工业轨道[2]以及板材[3]等的现场检测与实时监测。最新研究表明，超声导波技术甚至具有应用于包括人体长骨[4-6]以及血管、心肌[7]等层状或管状软组织在内的多层复杂波导结构与材料特性评价的前景。同时，利用超声导波的非线性效应[8]，还能对包括人体长骨组织在内的波导材料疲劳状况进行评价[9]。但受到导波多模式混叠与模式转换等因素的影响，导波模式分离与频散实验测量一直是研究的热点与难点[10-13]。应用时域反转技术能够获得相对简单的导波模式脉冲，并可能有助于长骨皮质骨裂纹评价[14-15]。但是传统的时间反转技术并未解决单一模式导波的选择性激发问题，接收到的时间反转信号仍会受到多模式的困扰。最近提出的频散反转技术虽可选择性激励单一模式脉冲[16]，但需要已知材料的特性与结构形状，在诸如长骨等复杂不规则结构的实践中仍有一定困难。频散曲线的准确测量是上述应用的工作基础[6,17]。

实验中导波频散测量方法为用二维傅里叶变换(2DFT)将阵列接收探头所测得的时间与距离矩阵变换至频率与波数域，依据模式能量的分布实现曲线求解[18]。该求解方法易受到噪声水平以及频率混叠的影响，特别是接收通道数量限制了不同位置的采样点数量，从而限定了波数测量分辨率。如何从较少的距离采样通道中估计波数实质上等效于经典的谱估计问题。同时，阵列导波信号在波数上具有明显的稀疏性，这确保了波数估计的合理性[17,19]。现已提出一些基于导波信号稀疏性增强频散曲线的方法，如基于稀疏SVD法的频散曲线提取技术[20]以及高分辨率的Radon变换法[21]。但将经典谱估计技术应用于导波频散曲线提取以及基于频散曲线估计材料参数的研究仍待继续深入。

经典的谱估计方法大体可分为非参数估计法、参数估计法以及子空间估计法等[22]。非参数估计法是从信号中直接估计功率谱密度函数，典型的有周期图法以及加窗改进后的Welch法。参数估计法的基本思想是将时域信号视为一个线性系统的冲击响应，典型的有Yule-Walker法与Burg法，其主要实现原理均为通过线性系统的传递函数进行功率谱估计。当信号采样点数较少时，参数估计法能获得优于经典非参数谱估计法的效果。本研究旨在将参数功率谱估计法应用于波数频率的测量，提高波数谱分辨力，进而结合不同厚度的铝板实验，分析算法性能并初步讨论导波频散估计板厚的可行性。

1 理论与方法

1.1 导波频散理论

板状材料中因横波纵波的多次反射与转换，会产生新的稳定传播的波包，通常被称为Lamb波[23]。根据其振动形态可分为对称模态与反对称模式，常被简写为An模式与Sn模式，数字n用于表示模式阶数。若板材厚度为2h，其横、纵波速度分别为VL与VT，则其Lamb频散方程可定义为

对称模式

(k2-q2)2tan(qh)+4k2pqtan(ph)=0

(1)

(k2-q2)2tan(ph)+4k2pqtan(qh)=0

(2)

(3)

(4)

满足上式的波数k与角频率ω的解被称为Lamb频散曲线。式(4)给出了波数与相速度VP的变换关系。

1.2 频散信号传递函数

阵列导波信号g(t,x)与波数和频率能量谱H(k,ω)满足2DFT关系[18]，即有

(5)

式中：t与x分别为时间与距离。导波频散曲线的测量实质上是从不同位置处的测量矩阵g(t,x)中估计波数频率域中H(k,ω)的问题。而H(k,ω)在各点处的能量分布则反映该组测量中各波数频率处信号的能量。实验中，时间的记录点通常比较充分，然而距离的记录点则有赖于测量范围、探头尺寸以及阵列单元等因素。在超声导波的测量系统中，通常只有数十个或者上百个测量单元，相对有限，距离上的移动既费时也不适于工业现场需要[24-25]。该局限性对波数的估计问题提出了客观需要。

1.3 谱估计技术

现代谱估计技术已有长足的进步，但是目前不少导波研究中仍往往采用经典的二维傅氏变换法求解频散问题，这并不能实现波数的最优估计。因而有必要吸收谱估计技术的发展成果加以改进。导波频散过程可视为一个线性系统响应。线性系统响应估计中最常用的是全极点模型，该模型对于白噪声的输入可视为自回归过程，所以基于全极点模型的谱估计法又被称为自回归谱估计，相关实现方法[22]在此不做赘述。其主要优点是在较少的采样点数下也可以获得很高的估计精度，这正适用于导波测量所面临的如何用较少的距离采样点估计较为稀疏的波数的问题。本文将比较两种基础的自回归谱估计技术，Yule-Walker法与Burg法[22]。其中，Yule-Walker法基于Levinson算法实现线性系统响应的无偏估计；而Burg法采用最小化前后向估计误差的方式从而避免了求解自相关函数，它能在保证计算效率的同时实现高精度谱估计。

通过口袋书和口头解答的方式，为群众提供便民咨询，工作人员为群众提供办事指导，实现了“让群众少跑一趟”的目标。

1.4 实验参数

本文采用轴向传输法分别测量3.0，4.0和5.0mm厚铝板中的多通路超声Lamb信号，材料参数见表1。根据式(1)和 (2)可解析计算出铝板中的理论波数-频率频散曲线和相速度-频率频散曲线。

表1 铝板材料参数

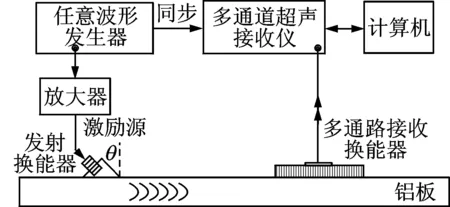
图1 实验框图Fig.1 Block diagram of experiments

图1为超声Lamb测量的实验框图。由任意波形发生器(33220A, Agilent, CA, USA)激励出中心频率为2 MHz，1周期的高斯窗调制源信号，经由放大器后输入到发射换能器(AT014, Valpey-Fisher, MA, USA)。本实验中发射换能器的中心频率为1 MHz，倾斜角度为45°。铝板中超声Lamb信号由多通道超声换能器(P4-1, Bothell, WA, USA)转化为电信号后，接入多通道超声接收仪(Vantage-128, Verasonics, WA, USA)采集数据，并在计算机中作进一步处理。接收换能器的-3 dB频带范围为1.0～4.0 MHz，共96个通道，相邻通道的间隔为0.25 mm。发射与接收换能器之间的距离为60 mm。

2 结果与讨论

2.1 铝板中阵列探头测量结果与2DFT计算结果

图2 铝板中多通路超声Lamb波距离-时间图 Fig.2 Distance-time plot of multi-channel ultrasonic Lamb wave in aluminum plate

图4 Yule-Walker法计算结果和理论频散曲线Fig.4 Results of Yule-Walker method and theoretical dispersion curves

图5 Burg法计算结果和理论频散曲线Fig.5 Results of Burg method and theoretical dispersion curves

以5 mm厚铝板为例，分别给出其超声Lamb时域信号，以及2DFT计算结果。图2为5 mm厚铝板中96通道超声Lamb距离-时间图；图3(a)为2DFT法算得的波数与频率模式能量分布，红色与蓝色分别表示高能量与低能量区域，白色为0。图3(a)中曲线系理论频散曲线(实线为反对称模式，虚线为对称模式)。图 3(b)为2DFT法计算结果，相速度与频厚积的关系；背景曲线为理论频散曲线，其中实线为反对称模式，虚线为对称模式。图3可知，主要获得了前10个基本导波模式，即对称模式S0至S4以及反对称模式A0至A4，但是用2DFT的方法仍有一些背景噪声。

2.2 改进的谱估计算法计算结果

以厚度为5 mm的铝板为例，给出两种谱估计方法的计算结果。Yule-Walker与Burg谱估计法波数与相速度计算结果如图4所示，Burg法的计算结果见图5。可见Yule-Walker法与Burg法都有效地抑制了背景噪声。图6给出了3种方式的幅度对比结果。图6(a)为波数为3.5 rad/mm时，3种方法算得的频谱结果，图中的3个峰值分别对应了A2，S2与A3模式。图6(b)为2.8 MHz时3种方法计算出的波数谱结果，两个峰值依次对应了A3与S2模式。可见，Burg法和Yule-Walker法均增强了波数与频率轴的谱线的计算精度，显著地压缩了谱线宽度，波数与频率谱线都较为锐利。但值得注意的是两种谱估计方法也会改变谱线的幅度。如图6(a)所示，2.64 MHz处的A3模式谱峰在Burg法和Yule-Walker法估计结果中接近于0。又如图6(b)所示，在2.8 MHz时，3.9 rad/mm波数处的A3模式谱峰相对幅度相比于2DFT结果从0.66降至0.22。

图6 2DFT法、Burg法和Yule-Walker法计算结果比较Fig.6 Comparison of computation results by three methods (2DFT, Yule-Walker and Burg)

2.3 厚度估计

从波数、频率能量图估计板厚的问题，可通过构造一系列不同厚度的频散曲线掩模矩阵来解决。在某一厚度下，计算包入掩模矩阵的频散能量与总能量的百分比(掩模能量百分比)，以及包入掩模矩阵能量与掩模区域面积之比(掩模能量密度)，当两者都达到最大时就对应了最优的厚度估计值。本文将两个比值的乘积曲线，归一化后用于厚度参数估计。图7给出了对3，4和 5 mm厚铝板，利用2DFT法、Burg法和Yule-Walker法的板厚估计结果。可看出，3种方法的板厚估计曲线均在相同的厚度估计值下达到了最大，对应于3块铝板的最优厚度估计值分别为3，3.75和4.75 mm，相应的误差百分比为0%， 6.25%和5%，逆问题求解中所用的估计精度为0.05 mm。

3种方法都较好地实现了板厚的估计。与2DFT法相比，Burg法和Yule-Walker法的厚度估计结果具有更好的对比度。值得注意的是，直接用模式能量面积与频散曲线相匹配的方法也可能会给出错误的估计结果。如图7(a)中，3 mm厚度铝板的结果在6 mm附近有一个较强的峰值。这是由于当厚度增加时，频散曲线掩模所覆盖的面积也在增加，而6 mm时正好将大多数能量都包在一组更密的频散曲线掩模之中，虽然模式能量密度也会下降，但是在这一组数据中下降并不明显，其部分原因为计算中固定了掩模矩阵的模式个数，随着厚度增加，掩模矩阵的面积并未大幅增加，因而导致了一些计算误差。

本文只讨论了两种比较经典的谱估计方法。还有改进的参数谱估计方法以及子空间谱估计方法，甚至比较新颖的稀疏谱估计方法等。但是从实验结果来看，参数谱估计方法已经较好地实现了高分辨率的超声导波频散曲线估计并可以实现比较准确的板厚估计。本实验结果的信噪比较高，一些实际条件下的测量可能会面对较复杂的低信噪比的情况[21]，未来应面向实际测量需要开展相关的探索。本文的不足之处主要在于从频散能量到板厚估计之间的逆问题仍有一定的误判可能性，应改进逆问题求解技术获得更为准确的估计精度，以更好地服务于工业现场检测的需要。

3 结束语

本文以参数谱估计法中的Yule-Walker法与Burg法为例实现了高分辨率铝板中超声导波频散曲线求解，进而分析了铝板厚度评价。结果表明，2DFT方法获得的结果对低能量谱线有较好的识别性，缺点是谱线较宽；Yule-Walker法与Burg法所获得的谱估计结果更为稀疏，但也容易在降噪的同时去除了低能模式能量。总体而言，参数谱估计法较2DFT法能获得更为准确的厚度估计结果，本研究对基于超声导波技术的无损检测有一定帮助。

[1] Su Z Q, Ye L. Identification of damage using Lamb waves: From fundamentals to applications[M]. Berlin: Springer, 2009.

[2] Hong M, Wang Q, Su Z Q, et al. In situ health monitoring for bogie systems of CRH380 train on Beijing-Shanghai high-speed railway[J]. Mechanical Systems and Signal Processing, 2014, 45(2):378-395.

[3] Li W B, Cho Y, Achenbach J D. Detection of thermal fatigue in composites by second harmonic Lamb waves[J]. Smart Materials and Structures, 2012, 21(8): 085019.

[4] Foiret J, Minonzio J G, Chappard C, et al. Combined estimation of thickness and velocities using ultrasound guided waves:A pioneering study on in vitro cortical bone samples[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2014, 61(9): 1478-1488.

[5] Xu K L, Liu D, Ta D A, et al. Quantification of guided mode propagation in fractured long bones[J]. Ultrasonics, 2014, 54(5): 1210-1218.

[6] Xu K L, Ta D A, He R X, et al. Axial transmission method for long bone fracture evaluation by ultrasonic guided waves: Simulation, phantom and in vitro experiments[J]. Ultrasound in Medicine and Biology, 2014, 40(4): 817-827.

[7] Urban M, Pislaru C, Nenadic I, et al. Measurement of viscoelastic properties of in vivo swine myocardium using Lamb wave dispersion ultrasound vibrometry (LDUV)[J]. IEEE Transactions on Medical Imaging, 2012, 32(2): 247-261.

[8] Deng M X. Cumulative second-harmonic generation of Lamb-mode propagation in a solid plate[J]. Journal of Applied Physics, 1999, 85(6): 3051-3058.

[9] Zhang Z Z, Liu D, Deng M X, et al. Experimental observation of cumulative second-harmonic generation of Lamb waves propagating in long bones[J]. Ultrasound in Medicine and Biology, 2014, 40(7): 1660-1670.

[10]Xu K L, Ta D A, Wang W Q, et al. Multiridge-based analysis for separating individual modes from multimodal guided wave signals in long bones[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2010, 57(11): 2480-2490.

[11]Song X J, Ta D A, Wang W Q. Analysis of superimposed ultrasonic guided waves in long bones by the joint approximate diagonalization of eigen-matrices algorithm[J]. Ultrasound in Medicine and Biology, 2011, 37(10): 1704-1713.

[12]Xu K L, Ta D A, Moilanen P, et al. Mode separation of Lamb waves based on dispersion compensation method[J]. Journal of the Acoustical Society of America, 2012, 131(4): 2714-2722.

[13]Zhao Ming, Zeng Liang, Lin Jing, et al. Mode identification and extraction of broadband ultrasonic guided waves[J]. Measurement Science and Technology, 2014, 25(11): 115005.

[14]Ing R K, Fink M. Time-reversed Lamb waves[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1998, 45(4): 1032-1043.

[15]刘洋，郭霞生，章东，等．基于时间反转的骨裂纹超声成像模拟研究[J]．声学学报，2011，36(2)：179-184．

Liu Yang, Guo Xiasheng, Zhang Dong, et al. A simulation study of ultrasonic imaging of micro-crack in bone based on time-reversed approach[J]. Acta Acustica, 2011, 36(2): 179-184.

[16]Xu K L, Ta D A, Hu B. Wideband dispersion reversal of Lamb waves[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2014, 61(6): 997-1005.

[17]Harley J B, Moura J M F. Sparse recovery of the multimodal and dispersive characteristics of Lamb waves[J]. Journal of the Acoustical Society of America, 2013, 133(5): 2732-2745.

[18]Alleyne D, Cawley P. A two-dimensional Fourier transform method for the measurement of propagating multimode signals[J]. Journal of the Acoustical Society of America, 1991, 89(3): 1159-1168.

[19]Minonzio J G, Talmant M and Laugier P. Guided wave phase velocity measurement using multi-emitter and multi-receiver arrays in the axial transmission configuration[J]. Journal of the Acoustical Society of America, 2010, 127：2913-2919.

[20]Xu K L, Minonzio L G, Ta D A, et al. Sparse SVD method for high resolution extraction of the dispersion curves of ultrasonic guided waves[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 2016, 63：1514-1524.

[21]Xu K L, Ta D A, Cassereau D, et al. Multichannel processing for dispersion curves extraction of ultrasonic axial-transmission signals: Comparisons and case studies[J]. Journal of the Acoustical Society of America, 2016, 140：1758-1770.

[22]Castanié F. Digital spectral analysis: Parametric, non-parametric and advanced methods[M]. London:ISTE Ltd, 2010.

[23]Viktorov I A. Rayleigh and Lamb waves: Physical theory and applications[M]. New York: Plenum Press, 1967.

[24]Harley J B, Moura J M. Data-driven matched field processing for Lamb wave structural health monitoring[J]. Journal of the Acoustical Society of America, 2014, 135(3): 1231-1244.

[25]Ngo S, Minonzio J G, Legros M, et al. A capacitive micromachined ultrasonic transducer probe for assessment of cortical bone[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2014, 61(4): 710-723.

张正罡 (1990-)，男，博士研究生，研究方向：医学非线性超声和图像处理。

胡波(1968-)，男，教授，博士生导师，研究方向：数字图像处理、信息传输与数字通信和数字系统设计等。

刘丹(1991-)，男，硕士研究生，研究方向：医学非线性超声和编码技术。

High-Resolution Ultrasonic Lamb Waves Dispersion Measurement and Plate Thickness Evaluation

Xu Kailiang1, Zhang Zhenggang2, Liu Dan2, Ta Dean2,3, Hu Bo2

(1.Laboratoire d′Imagerie Biomedicale(LIB), Sorbonne Universites, UPMC Univ Paris 06,CNRS,INSERM,75006, Paris, France; 2. Department of Electronic Engineering, Fudan University, Shanghai, 200433, China; 3. Key Lab of Med Imag Computing and Computer Assisted Intervention (MICCAI) of Shanghai, Shanghai, 200032, China)

As one of the most promising technologies, ultrasonic Lamb waves have been widely analyzed in the non-destructive evaluation. However, due to the guided dispersion and mode overlap, mode identification and dispersion determination are still challenging, thereby attacting considerable attentions. Here, we use two traditional spectrum estimation methods, i.e., the Yule-Walker method and the Burg method to analyze the array-transducer signals for high-resolution ultrasonic Lamb waves dispersion measurement. An inverse method was also designed to estimate the aluminum plate thickness from the extracted wideband dispersion curves. Experiments on three aluminate plates with different thicknesses (3 mm, 4 mm and 5 mm) demonstrated that the spectrum estimation methods were helpful for the ultrasonic Lamb waves based non-destructive evaluation.

ultrasonic Lamb waves; traditional spectrum estimation methods; dispersion curves; thickness estimation; non-destructive evaluation

国家自然科学基金(11304043,11327405，11525416)资助项目。

2015-01-08；

2015-03-16

R445.1