一种改进型DRNN神经网络自学习PID控制

刘甘霖+沈玲+左是

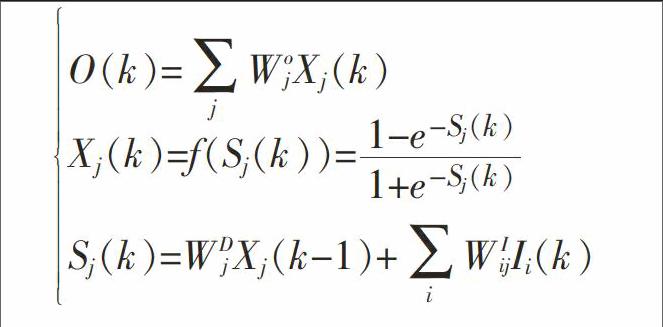
摘 要： 本文针对多变量耦合系统，采用DRNN神经网络对PID控制器参数进行自学习，提出了将学习因子在学习过程中进行动态调整，与传统DRNN神经网络自学习PID控制整定结果进行比较，使用matlab进行仿真，仿真结果表明，学习因子动态调整后的参数结果在超调量、调节时间、稳态性能上明显优于传统DRNN算法。

关键词： DRNN；收敛；学习速率；matlab；仿真

中图分类号： TP183 文献标识码： A 文章编号： 2095-8153（2016）06-0104-04

在工业被控对象中，具有多变量强耦合特性的较多，对其进行控制必须采取一定的解耦措施，否则难以取得满意的控制效果，现代控制理论提供的一般方法是需要知道被控对象的相关参数，进行解耦再设计控制器[1][2]。其控制器设计方法较复杂，而且依赖被控对象精确的数学模型，在实际现场中很难获得。

本文采用一种优化学习速率的对角递归神经网絡（DRNN）对多变量耦合系统进行动态辨识，学习算法采用梯度下降法，在传统DRNN算法的网络学习过程中对学习速率？浊I、？浊D、？浊O进行动态调整，使得比传统算法具有更快的收敛速度。由DRNN获得敏感信息？坠y/？坠u可以在线调整PID控制器参数，从而利用传统的PID控制器输出控制量到被控对象，并完成系统的解耦与控制工作。使用matlab对其进行仿真，仿真结果表明对学习速率进行动态调整后PID参数调整时间有所降低，使系统的动态性能有所加强。

1 对角神经网络（DRNN）及其算法改进

1.1 DRNN基本结构

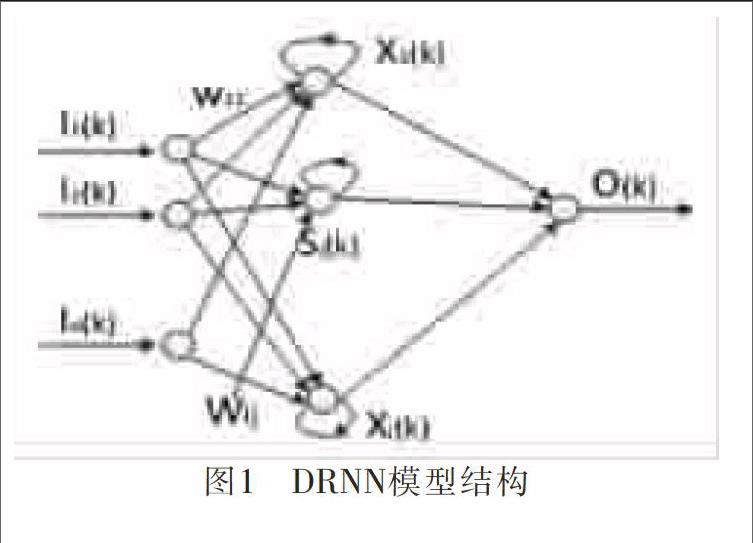
DRNN是在部分递归网络Elman网的基础上，将隐含层权值矩阵WD进一步简化为对角矩阵，即隐含层的每一个神经元仅接受自己输出反馈，而与其他神经元无反馈连接。DRNN的模型结构如图1所示。

在DRNN神经网络中，设I=[I1，I2，…In]为网络输入向量，Ii（k）为输入层第i个神经元的输入，网络回归层第j个神经元的输出为Xj（k），Sj（k）为第j个回归神经元输入总和，f（*）为S函数，O（k）为DRNN网络的输出。DRNN神经网络算法为：

O（k）=■WojXj（k）Xj（k）=f（Sj（k））=■Sj（k）=WDjXj（k-1）+■WIijIi（k）（1）

式1中，WD和WO为网络回归层和输出层的权值向量，WI为网络输入层的权值向量，O（k）为网络输出层输出，Xj（k）为网络回归层输出，Sj（k）为网络回归层输入。

1.2 DRNN网络辨识算法改进

辨识误差：em（k）=y（k）-O（k），其中y（k）为系统的实际输出，k为网络迭代步骤。辨识指标：Em（k）=■em（k）2

学习算法采用梯度下降法：

？驻woj（k）=-■=em（k）■=em（k）Xj（k）（2）

woj（k）=woj（k-1）+？浊O？驻woj（k）+？坠（woj（k-1）-woj（k-2））（3）

？驻wIij（k）=-■=em（k）■=em（k）■ ■=em（k）wojQij（k）（4）

wIij（k）=wIij（k-1）+？浊I？驻wIij（k）+a（wIij（k-1）-wIij（k-2））（5）

？驻wDj（k）=-■=em（k）■ ■=em（k）wojPj（k）（6）

wDj（k）=wDj（k-1）+？浊D？驻wDj（k）+a（wDj（k-1）-wDj（k-2））（7）

其中，Pj（k）=■=■Xj（k-1），Qij（k）=■=■Ii（k）

式中，？浊I、？浊D、？浊O分别为输入层、回归层和输出层的学习速率，？坠为惯性系数。对象的Jacobian信息为：

■≈■=■wOj■wIij

当学习速率？浊加大时，可使收敛速度加快，但易产生振荡和不稳定；反之，当？浊减小时，可维持算法的稳定但却可能导致缓慢收敛[3][4]。传统DRNN算法只取一组固定值。根据这一信息，对学习速率？浊进行动态调整，由于算法前期学习过程中可以快速收敛，以降低调节时间，在学习后期可以适当降低学习速率以达到输出稳定。本文对？浊调整的规则为依据误差变化率的绝对值选取适当的？浊值，其调整规则为：若em（k）的变化率的绝对值小于1，？浊I、？浊D、？浊O取一组较小值，反之取一组较大值。

2. DRNN神经网络参数自学习PID控制策略

本文的控制策略由DRNN作为辨识器，根据系统信息的变化，对权值进行自动调整，DRNN获得Jacobian信息进行在线调整PID控制器的比例、积分、微分系数[5]。系统仍由PID控制器控制，其结构如图2所示。

以控制器u1为例，控制算法如下：

u1（k）=kp1（k）x1（k）+ki1（k）x2（k）+kd1（k）x3（k）（8）

error1（k）=r1（k）-y1（k）（9）

且有：x1（k）=error1（k）

x2（k）=■（error1（k）×T）

x3（k）=■

式中T为采样时间。PID三项系数kp1（k），ki1（k），kd1（k）采用神经网络进行整定。

定义如下指标：

E1（k）=■（r1（k）-y1（k））2（10）

kp1（k）=kp1（k-1）-？浊p■=kp1（k-1）+？浊p（r1（k）-y1（k））■ ■=kp1（k-1）+？浊p（r1（k）-y1（k））■x1（k） （11）

ki1（k）=ki1（k-1）-？浊i■=ki1（k-1）+？浊i（r1（k）-y1（k））■ ■=ki1（k-1）+？浊i（r1（k）-y1（k））■x2（k） （12）

kd1（k）=kd1（k-1）-？浊d■=kd1（k-1）+？浊d（r1（k）-y1（k））■ ■=kd1（k-1）+？浊d（r1（k）-y1（k））■x3（k）（13）

式中■为Jacobian信息，由DRNN网络进行辨识。

3 仿真分析

为了验证DRNN神经网络算法在学习过程中对学习因子进行动态调整后PID参数整定效果比传统DRNN算法整定效果更优，使用文献中所描述二变量耦合被控對象为例：

y1（k）=1.0/（1+y1（k-1））2（0.8y1（k-1）+u1（k-2）+0.2u2（k-3））y2（k）=1.0/（1+y2（k-1））2（0.9y2（k-1）+0.3u1（k-3）+u2（k-3））

设采样时间为1s，传统DRNN中学习速率？浊I=0.4、？浊D=0.4、？浊O=0.4，？坠=0.04。权值取[-1，+1]之间随机值。网络学习后Jacobian信息以及调整后的kp1，ki1，kd1以及kp2，ki2，kd2分别如图3、图5、图7所示。对于学习速率随em（k）的变化率动态调整后的Jacobian信息以及kp1，ki1，kd1以及kp2，ki2，kd2分别如图4、图6、图8所示。

从仿真结果可以看出，采用学习速率动态优化后的Jacobian信息明显比传统DRNN中收敛快，后期稳定性好。在整定kp1，ki1，kd1与kp2，ki2，kd2值达到稳定时间只需10 s，超调量明显减小。

4 结语

DRNN神经网络自学习PID控制在解耦控制、非线性控制中对PID参数进行在线整定的应用较多，不需要建立被控对象精确数学模型就能对其进行很好地控制，本文对传统DRNN神经网络的学习速率进行在线调整，并通过matlab仿真验证了改进型DRNN神经网络在PID参数整定上具有一定的优势性，其收敛速度明显加快，以及降低了超调量，稳态性能也得到加强。这对后续将模糊控制融入DRNN神经网络学习过程有一定的借鉴意义。

[参考文献]

[1]周东华，胡艳艳.动态系统的故障诊断技术[J].自动化学报，2009（06）：748-758.

[2]薛美盛，吴 刚，孙德敏，王 永.工业过程的先进控制[J].化工自动化及仪表，2002（02）：1-9.

[3]杨 青，党选举.基于DRNN的多变量解耦控制系统[J].自动化技术与应用，2004（03）：14-17.

[4]韩贵金.一种基于对角递归神经网络的PID解耦控制器[J].电子科技，2007（09）：22-26.

[5]王万召，李 利.钢球磨煤机制粉系统DRNN神经网络解耦控制研究[J].东北电力技术，2008（01）：23-25.

[6]刘金琨.先进PID控制及其MATLAB仿真[M].北京：电子工业出版社，2004：166-167.

Abstract： Self learning is made with Multivariable coupling system by DRNN neural network on PID controller parameters. This paper makes the comparison between dynamic adjustment of learning factor in the learning process and traditional DRNN neural network self-learning PID control setting the result. Mat-lab simulation is made for this comparison and the result shows that parameters adjusted dynamic of learning factor are superior to traditional DRNN algorithm in overshoot，adjustment time and steady state performance.

Key words： DRNN；convergence；learning velocity；mat-lab；simulation