交通环境振动测试数据中暗振动去除的ANFIS法*

耿传飞， 卢文良， 俞 醒

(1.北京交通大学土木建筑工程学院 北京，100044) (2.中铁第四勘察设计院集团有限公司 武汉，430063) (2.金丽温铁路有限责任公司 温州，325003)



交通环境振动测试数据中暗振动去除的ANFIS法*

耿传飞1，2， 卢文良1， 俞 醒3

(1.北京交通大学土木建筑工程学院 北京，100044) (2.中铁第四勘察设计院集团有限公司 武汉，430063) (2.金丽温铁路有限责任公司 温州，325003)

轨道交通引起的环境振动测试数据中混杂着暗振动的成分。提出了一种去除暗振动的自适应神经模糊推理系统(adaptive neuro-fuzzy inference system,简称ANFIS)法，阐述了其基本原理，给出了该法的具体实现步骤。通过一条列车引起的地面振动加速度时程与一条暗振动加速度时程叠加得到现场实测振动加速度时程，采用提出的ANFIS法及其他几种已有方法对该算例进行了去除暗振动的计算，并进行了对比分析。几种方法计算的时程均方根误差分别为：谱幅值修正法0.414 mm/s2，自功率谱法0.363 mm/s2，自互功率谱法0.261 mm/s2，ANFIS法0.074 mm/s2，可见，ANFIS法均方根误差最小；几种方法计算的加权振级VLz分别为：振动级修正法63.842 dB，谱幅值修正法62.894 dB，自功率谱法63.859 dB，自互功率谱法63.802 dB，ANFIS法63.805 dB，ANFIS法计算结果与真实交通振动值63.815 dB最接近。结果表明，在时程、傅里叶谱、功率谱密度及振动级的计算上，ANFIS法计算结果都与真实交通振动值非常接近，产生的误差比其他已有方法更小。

轨道交通；环境振动；测试数据；暗振动；自适应神经模糊推理系统法；自功率谱法；自互功率谱法

引 言

随着轨道交通建设的发展，交通引起的振动问题日益突出，国际上已把振动列为七大环境公害之一，逐步引起了人们的高度重视。振动会影响人的身心健康，影响精密仪器的正常运行，也可能对建筑物造成损害。为了直接获得轨道交通引起的地面振动数据，常采用的方法是现场实测[1-2]。现场实测数据往往不只是交通系统引起的振动，周围工厂的机器振动、附近工地施工引起的振动、地脉动以及由观测设备、观测方法产生的观测误差等都不可避免地掺杂进测试振动数据中，此类干扰振动或误差通常称为暗振动[3]。

目前，去除实测振动数据中暗振动的方法主要有4种：振动级修正法[4-6]去除暗振动，这种方法的缺点是不能得到真实的加速度时程和功率谱密度；Fourier谱幅值修正法[7](简称谱幅值修正法)去除暗振动；还有自功率谱法[3]和自互功率谱法[8]也可用于去除暗振动。以上4种都是基于频域分析的方法，而实测值是时域内的一系列离散数据，基于频域的数据处理方法需将时域数据转换到频域，不太方便。笔者提出基于时域分析的自适应神经模糊推理系统(ANFIS)法，具有简单、易行的特点，经算例验证，在去除暗振动方面具有很好的效果。

1 ANFIS法去除暗振动的基本原理

1.1 自适应神经模糊推理系统(ANFIS)

自适应神经模糊推理系统(ANFIS)是Roger[9]提出的一种将模糊推理系统和神经元网络相结合的产物。模糊推理系统能较好地仿效人的思维方式，反映和总结人的经验，神经网络具有自学习自适应的功能，ANFIS充分利用二者优良特性，具有以任意精度逼近任何线性或非线性函数的功能，且所需训练样本少、收敛速度快、结果误差小。ANFIS将模糊推理系统中的模糊逻辑规则和隶属度函数参数通过神经网络自学习来设定，自动产生模糊规则和调整隶属度函数，而不是基于经验或直觉给定，解决了控制精度不高、缺乏自学习能力等问题。ANFIS使用给定的输入输出数据集构建一个模糊推理系统，与神经网络相比，不仅有学习功能，而且可以表达模糊语言变量[10]。ANFIS是一种高木-关野(Takagi-Sugeno)型模糊推理系统，能自动产生“if-then”规则，其中，对于2个输入和1个输出的一阶Takagi-Sugeno型模糊系统，有以下2条规则[11]

(1)

以此类推，可以写出与模糊系统对应的多条if-then规则。

ANFIS结构图如图1所示：(a)为m个输入量x1,x2,…,xm和n条模糊if-then规则的情况；(b)为m=1,n=5的情形。图中方形节点表示其参数是可调节的，圆形节点表示其参数是不可调节的；节点间的连线仅表示信号的流向，没有权值与之关联。ANFIS的结构可分为5层。

图1 ANFIS结构图Fig.1 ANFIS structure diagram

第1层输入变量模糊化，输出对应模糊集的隶属度，其中每个节点的传递函数可表示为

(2)

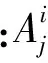
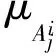
(3)

隶属函数的形状随这些参数的改变而改变。实际上，隶属函数可以取任意分段连续函数，如梯形函数或三角形函数。

第2层形成模糊化规则,输出每条规则的适用度，即将各输入信号的隶属度相乘，乘积作为本条规则的适用度

(4)

第3层各条规则的适用度归一化，即计算每条规则适用度与所有规则适用度之和的比值

(5)

第4层计算每条规则的输出

(6)

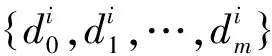
第5层计算模糊系统的总输出,即所有规则的输出之和

(7)

ANFIS采用反向传播算法和最小二乘估计算法的混合算法[12]来调整模糊系统的前提参数和结论参数，具体为：

1) 固定前提参数不变，逐层计算输入向量在网络中神经元节点的输出值直到第4层，用最小二乘公式进行辨识，得到结论参数；

2) 信号继续沿网络正向传递至输出层(即第5层)，采用得到的结论参数计算误差信号，再将误差信号从输出端反向传播，对前提参数进行调节，改变隶属度函数的形状。

这种混合算法对于给定的前提参数，可以得到结论参数的全局最优点，不仅降低了搜索空间的维数，通常还大大提高了参数的收敛速度。

1.2ANFIS法去除暗振动原理

(8)

展开，得

(9)

其中：<,>表示内积。

式(9)两边同除以振动时长T，得

(10)

即

(11)

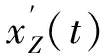
(12)

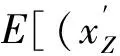
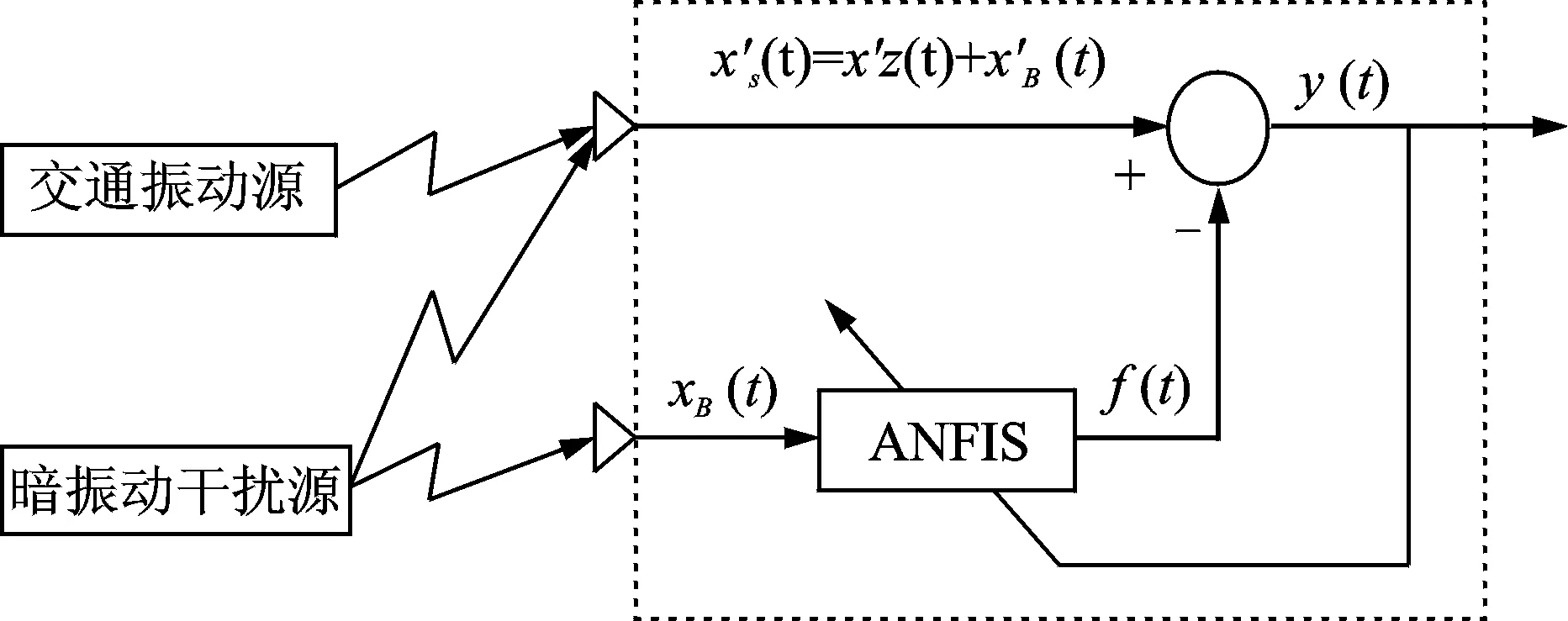
图2 ANFIS法原理图Fig.2 ANFIS schematic diagram

2 ANFIS法去除暗振动的实现方法

2.1 程序实现

编制程序实现时，采用Matlab中函数genfis1和anfis实现自适应神经模糊推理系统的初始化和训练。函数genfis1采用网格分割的方法，从给定的训练数据集生成一个初始模糊推理系统，初始模糊系统的输入输出隶属度函数的类型可以在函数中指定，也可以采用缺省值。函数anfis采用混合算法进行模糊系统的训练，在训练过程中，已经给定的初始模糊推理系统的结构即隶属度函数个数和模糊规则数目不会改变，只是对相应的结构参数进行调整和优化。完成模糊系统的训练后，利用evalfis函数计算对应的输出值就可以去除实测振动中的暗振动。

2.2 图形界面编辑器实现

通过Matlab图形界面编辑器实现时，首先利用anfisedit命令打开编辑器，加载指定输入输出数据文件作为训练数据，然后生成一个初始模糊推理系统，设定训练周期，对模糊推理系统进行训练，训练过程中不断调整隶属函数参数，并在编辑器窗口中动态显示训练数据对应误差随周期变化的曲线图，训练完成后，计算对应的输出结果。

本研究选用图形界面编辑器实现实测振动中暗振动去除的ANFIS法,将无车时的振动数据和实测振动数据保存在数据文件中，作为训练数据，对建立的初始模糊推理系统进行训练，每次输入赋予5个一般的钟形隶属函数(见式(3))，初始将训练周期数设定为50，得到误差随训练周期的增加逐渐减小，此时，将周期调为100。计算表明，训练开始阶段，误差随训练周期增加而变小，大约70个周期后误差已基本不再变化，说明选择的周期数是合适的，将训练好的模糊推理系统导出，计算对应的输出值就可进行去除实测振动中暗振动的处理。

3 算例验证及对比分析

3.1 算例简介

为了验证所提方法的可靠性，采用东华DHDAS5956测试仪对金温扩能改造工程V标段浦北桥现场振动加速度进行了实测，测试仪如图3所示，现场测试情况如图4所示。选取了一条振动加速度时程作为列车引起的地面振动(简称交通振动)，另选一条无车时的实测地面加速度时程作为暗振动，将交通振动和暗振动相加，人工合成现场环境振动(简称实测振动)。在工程中，无车时的振动和实测振动是可以测得的，去除暗振动的真实交通振动是未知的(本算例中的真实交通振动事先已知)。

图3 东华DHDAS5956测试仪Fig.3 Dong Hua DHDAS5956 test instrument

图4 现场测试图Fig.4 Field test diagram

3.2ANFIS方法与其他方法的对比分析

3.2.1 时程比较

图6分别给出了各种方法计算出的交通振动时程与真实交通振动时程的对比，为清晰的作比较，图中只截取了22.5～23．0s时间区间。不难看出，在某些时间段上，谱幅值修正法、自功率谱法和自互功率谱法计算的时程与真实振动时程曲线均有偏差，ANFIS法能够很好地改善这种偏差，得到的时程曲线与原真实曲线基本一致。

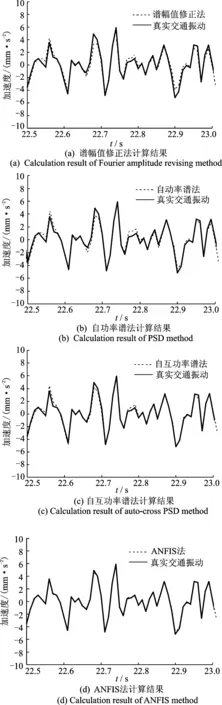
图6 加速度时程曲线比较Fig.6 Comparison of acceleration time history curves

进一步比较加速度时程的绝对误差，如图7所示，在大多数时间点上，ANFIS法的绝对误差比谱幅值修正法、自功率谱法和自互功率谱法均小。此外，几种方法计算出的交通振动加速度时程均方根误差分别为：0.414mm/s2(谱幅值修正法)、0.363mm/s2(自功率谱法)、0.261mm/s2(自互功率谱法)、0.074mm/s2(ANFIS法)，可以看出，ANFIS法误差最小。

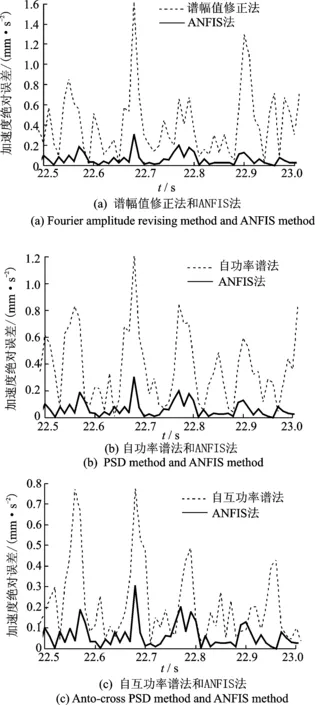
图7 加速度时程曲线绝对误差Fig.7 Absolute errors of acceleration time history curves

3.2.2 傅里叶谱比较

傅里叶谱分析法在工程振动数据分析中被广泛运用，图8是真实交通振动的傅里叶谱与各种方法计算的傅里叶谱对比，为了方便查看，图中截取了6.7～8.2Hz频率段。由图8知，谱幅值修正法计算出的傅里叶谱与真实值偏差较大；自功率谱法计算出的傅里叶谱与真实值之间偏差略微减小，但仍有一定偏差；自互功率谱法计算傅里叶谱与真实值之间偏差较小；ANFIS法计算出的傅里叶谱与真实值基本一致，符合较好。进一步比较自互功率谱法和ANFIS法计算的傅里叶谱，将二者计算傅里叶谱的绝对误差绘于图9中，由图9知，ANFIS法计算傅里叶谱绝对误差值在大多数频率点上小于自互功率法，表明ANFIS法计算结果更加准确。

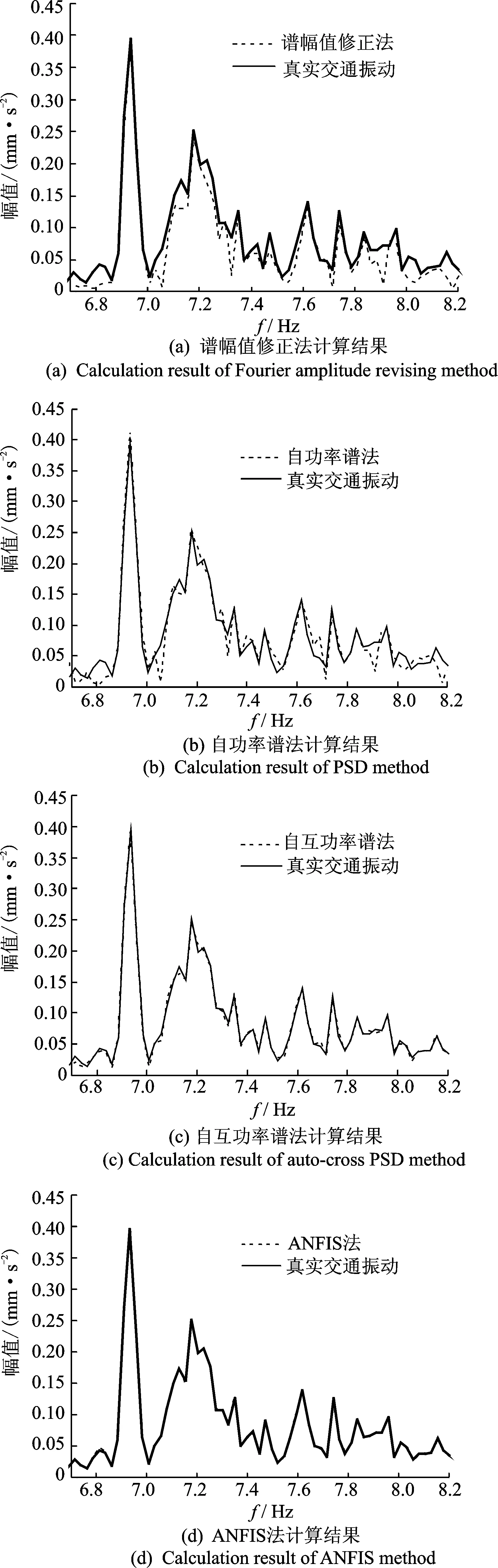
图8 傅里叶谱曲线比较Fig.8 Comparison of Fourier spectrum curves

图9 傅里叶谱曲线绝对误差Fig.9 Absolute errors of Fourier spectrum curves

3.2.3 功率谱密度比较

功率谱密度也是研究环境振动影响的一个重要手段，图10分别显示了ANFIS法和其他几种方法计算的功率谱密度曲线与真实交通振动的功率谱密度曲线的对比。为了方便查看，图中截取了6.7～8.2Hz频率段。由图10可知，谱幅值修正法计算结果与真实值偏差较大，自功率谱法计算结果也有一定偏差，自互功率谱法计算结果能减小这种偏差，而文中提出的ANFIS法计算结果与真实值较为一致，产生的偏差较小，表明ANFIS法是可靠的。为进一步比较自互功率谱法和ANFIS法计算的功率谱密度，将功率谱密度绝对误差计算结果绘于图11中，可以看出，在大多数频率点上，ANFIS法的绝对误差都要小于自互功率谱法。

3.2.4 振动级比较

几种方法计算的1/3倍频程中心频率处的振动加速度级与真实交通振动的振动加速度级对比示于图12中，可以看出，谱幅值修正法与真实交通振动的振动加速度级偏差较大，在大多数频率处低于真实值，表明谱幅值修正法在去除暗振动过程中过多削弱了实测振动；在某些频率处，振动级修正法和自功率谱法与真实交通振动加速度级也有偏差；ANFIS法在整个频率段都符合得较好，与真实交通振动加速度级较为一致。

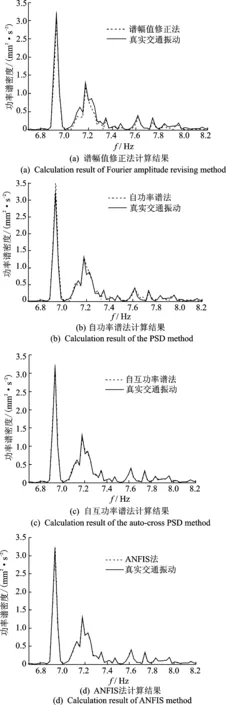
图10 功率谱密度曲线比较 Fig.10 Comparison of power spectral density curves

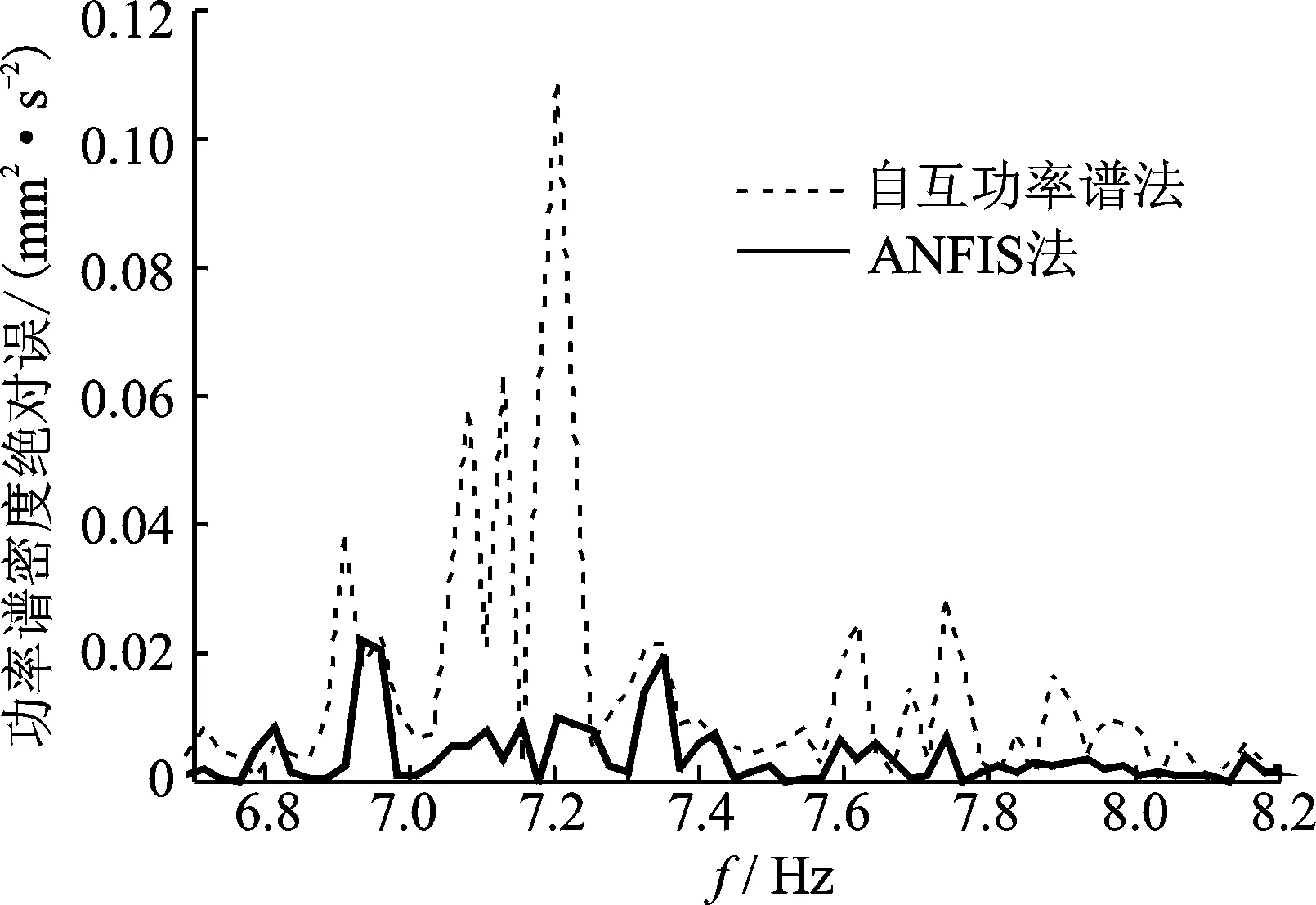
图11 功率谱密度曲线绝对误差Fig.11 Absolute errors of power spectral density curves

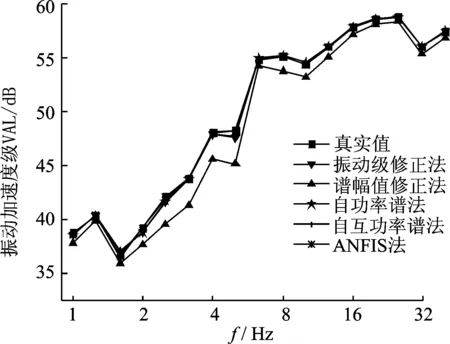
图12 振动加速度级比较 Fig.12 Comparison of vibration acceleration levels

图13为各1/3倍频程中心频率处振动加速度级绝对误差值对比，由图13可知，谱幅值修正法无论是在高频段，还是在低频段，计算的振动加速度级误差都相对比较大，在8Hz以下表现更加明显；振动级修正法和自功率谱法在8Hz以上符合较好，但在8Hz以下频段，误差也比较大；自互功率谱法和ANFIS法在整个频段内，符合都比较好。

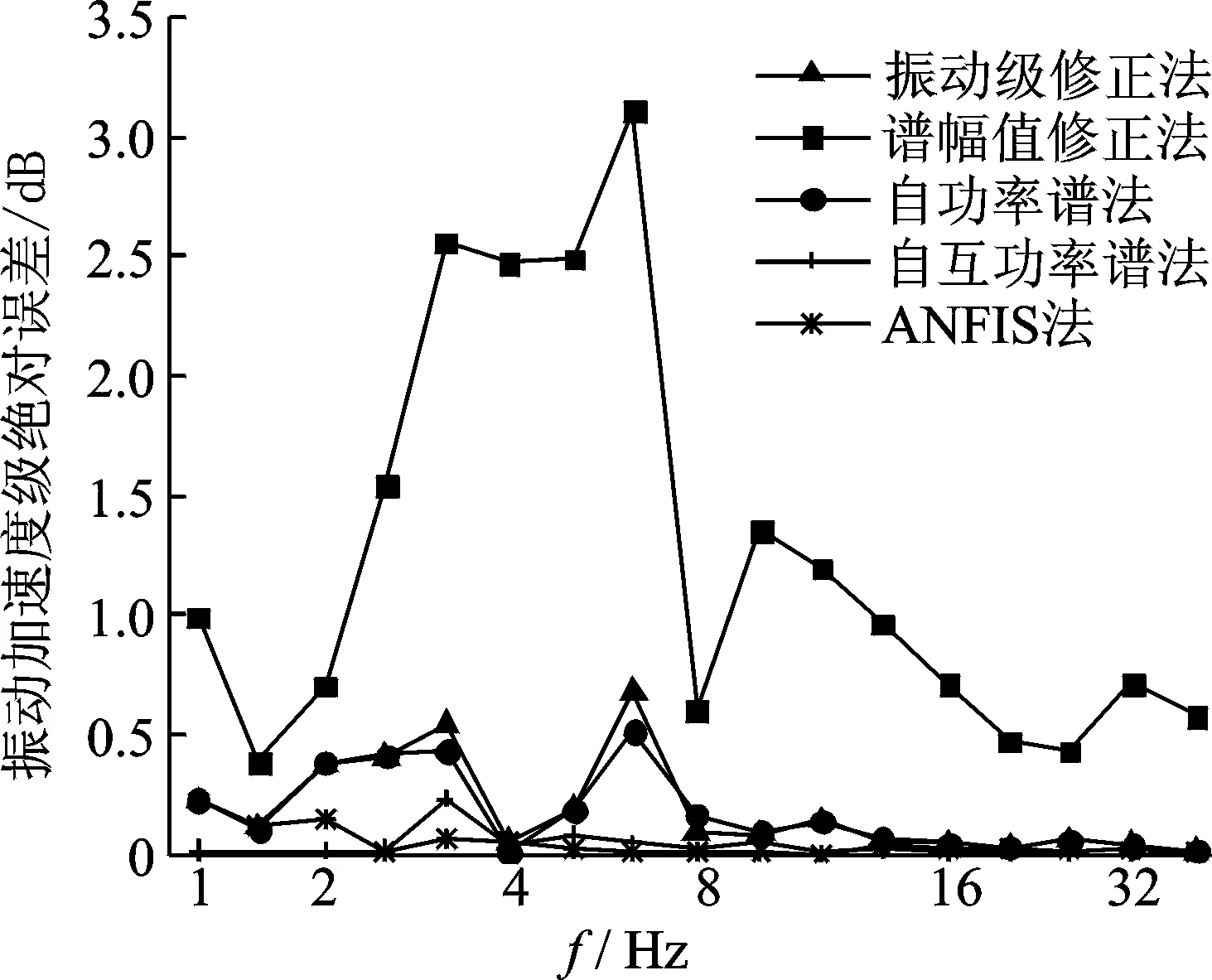
图13 振动加速度级绝对误差Fig.13 Absolute errors of vibration acceleration levels

经计权因子处理后的振级VLz分别为：63.842(振动级修正法)，62.894(谱幅值修正法)、63.859(自功率谱法)63.802(自互功率谱法)及63.805dB(ANFIS法)，与真实交通振动63.815dB相比，自互功率谱法和本研究的ANFIS法与真实值最为接近，进一步比较，ANFIS法计算的振级误差最小。

4 结束语

ANFIS法可以有效地将实测振动中的暗振动剥离出去，得到真实交通振动的时程曲线、傅里叶谱曲线、功率谱密度曲线和振动级，为进一步研究交通环境振动提供数据支持。笔者提出的ANFIS法与谱幅值修正法、自功率谱法、自互功率谱法等去除暗振动方法相比，无论是在时程、傅里叶谱和功率谱密度计算上，还是在振动级的计算上，计算结果都更加准确、可靠。

[1] 盛涛，张善莉，单伽钲，等.地铁诱发的环境振动及振源减振效应的实测与分析[J].振动、测试与诊断，2015,35(2):352-358.

Sheng Tao, Zhang Shanli, Shan Jiazheng, et al. In-situ measurement and analysis of subway-induced environmental vibrations and the effectiveness of vibration-source suppression methods[J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(2): 352-358. ( in Chinese)

[2] 常乐，闫维明，任珉，等.高架路交通诱发的地面振动测试与分析[J].振动、测试与诊断,2009,29(2):175-178.

Chang Le, Yan Weiming, Ren Min, et al. Test and analysis of ground vibration induced by elevated road traffic[J]. Journal of Vibration, Measurement & Diagnosis, 2009,29(2):175-178. ( in Chinese)

[3] 福彤，陶夏新，郑鑫，等. 交通环境振动观测中本底振动去除的功率谱修正法[J].振动与冲击，2011,30(4):124-126,172.

Wang Futong, Tao Xiaxin, Zheng Xin, et al. PSD correction method for removing background vibration from traffic environmental vibration observation[J]. Journal of Vibration and Shock, 2011,30(4):124-126,172. ( in Chinese)

[4] 张昕.高架轨道交通引起环境振动的实测和理论分析研究[D].上海：同济大学，2002.

[5] 邱俊杰.高架轨道交通引起环境振动的实测与评价方法研究[D].武汉：武汉理工大学，2005.

[6] 崔高航，陶夏新，陈宪麦.城轨交通地面线路产生环境振动频域分析[J].沈阳建筑大学学报：自然科学版，2008,24(2)：239-243.

Cui Gaohang, Tao Xiaxin, Chen Xianmai. Analysis of environmental vibration induced by urban rail transit on ground in frequency domain.[J]. Shenyang Jianzhu University：Natural Science, 2008,24(2): 239-243. (in Chinese)

[7] 张向东，闫维明，任珉，等.交通环境振动测试中的本底振动分析[J].振动与冲击，2009,28(4)：177-179,197.

Zhang Xiangdong, Yan Weiming, Ren Min, et al. Background vibration analysis for traffic environmental vibration testing[J]. Journal of Vibration and Shock, 2009,28(4)：177-179,197. ( in Chinese)

[8] 郑鑫，陶夏新，王福彤，等.去除交通环境振动观测记录中本底振动的自互功率谱法[J].地球物理学报，2013,56(1):348-353.

Zheng Xin, Tao Xiaxin, Wang Futong, et al. An auto-cross PSD method to remove background vibration from observational records of traffic environment vibration[J]. Chinese Journal of Geophysics, 2013,56(1):348-353. ( in Chinese)

[9] Roger Jang J S. ANFIS: adaptive-network-based fuzzy inference system[J].IEEE Transactions on Systems, Man and Cybernetics, 1993,23(3):665-685.

[10] 王卓，王艳辉，贾利民，等.基于ANFIS的高速列车制动控制仿真研究[J].铁道学报,2005,27(3):113-117.

Wang Zhuo, Wang Yanhui, Jia Limin, et al. Study on high-speed train braking control simulation based on ANFIS[J]. Journal of the China Railway Society， 2005,27(3):113-117. ( in Chinese)

[11] 马细霞，郭慧芳，陈鑫.基于ANFIS的水质评价模型及其应用[J].水资源保护，2007,23(6):12-14,69.

Ma Xixia, Guo Huifang, Chen Xin. Water quality evaluation model based on ANFIS and its application[J]. Water Resources Protection, 2007,23(6):12-14,69. ( in Chinese)

[12] 梁得亮，丁文，鱼振民.基于自适应网络模糊推理系统的开关磁阻电机建模方法[J].中国电机工程学报，2008,28(9)：86-92.

Liang Deliang, Ding Wen, Yu Zhenmin. Modeling for switched reluctance motor based on adaptive network-based fuzzy inference system[J]. Proceedings of the CSEE, 2008,28(9)：86-92. ( in Chinese)

*中央高校基本科研业务费专项资金资助项目(2011JBM275)

2015-03-10；

2015-07-21

10.16450/j.cnki.issn.1004-6801.2017.02.029

X593；TH113．1

耿传飞，男，1990年10月生，硕士、助理工程师。主要研究方向为桥梁结构理论与应用、轨道交通环境振动控制等。曾发表《Test study on ground vibration induced by moving trains on existing bridges》(《Construction and Maintenance of Railway Infrastructure in Complex Environment: The 3rd International Conference on Railway Engineering (ICRE2014)》, Beijing: China Railway Publishing House,2014)等论文。 E-mail:cfgeng@163.com