新型机械弹性车轮包容特性的力学研究*

王 强， 赵又群， 林 棻， 杜现斌， 付宏勋

(南京航空航天大学能源与动力学院 南京，210016)



新型机械弹性车轮包容特性的力学研究*

王 强， 赵又群， 林 棻， 杜现斌， 付宏勋

(南京航空航天大学能源与动力学院 南京，210016)

利用有限元分析和试验测试方法对新型机械弹性车轮的包容特性进行了力学研究。通过平面及障碍物作用下车轮垂向力学特性的分析，揭示了障碍物截面形状对车轮垂向力学响应的影响规律，并验证了所建模型的可靠性。基于车轮非线性有限元模型和台架试验，分析了车轮在三种不同截面障碍物作用下的低速稳态包容特性，并研究了车轮通过障碍物后的垂向和纵向动态力学响应的变化规律，及负荷和障碍物截面形状对包容特性的影响。结果表明：车轮垂向力响应随负荷的增加由抛物线形过渡到马鞍形，车轮纵向力响应随负荷的增加而增大，其变化曲线类似为正弦形状；且车轮垂向力和纵向力响应随障碍物高度的增加而增大；其响应峰值相对较低、变化较平缓，在一定载荷条件下，车轮表现出典型的包容特性。

机械弹性车轮； 包容特性； 垂向刚度； 障碍物； 力学响应

引 言

轮胎作为汽车的主要组成部件，其结构参数和力学特性直接影响到车辆的操纵稳定性、动力性及平顺性等性能。但当轮胎刺破受损时，会造成车辆通过性降低，甚至丧失机动性能，且高速行驶时还存在爆胎隐患，为了改变现有轮胎状况，安全轮胎技术越来越受到轮胎工业的重视。因此，国内外学者研发了不同结构的非充气轮胎，但存在自重和刚度较大、加工工艺复杂和散热难等问题，仍处于概念研发阶段。为解决以上问题，本课题组提出了一种新型非充气弹性车轮，该车轮是通过机械弹性复合连接结构代替传统轮胎的充气弹性结构，在实现充气轮胎基本功用的同时，能够避免刺扎、爆胎和爆损等问题，所以该弹性车轮更满足于特种车辆(军事车辆、越野车及抢险救灾车等)的安全使用要求。

当轮胎滚动时，轮胎对路面不平度及来自路面的垂直作用力进行滤波的特性称为轮胎包容特性，轮胎包容特性随轮胎结构、尺寸和负荷大小的变化而变化，国内外学者就充气轮胎的包容特性已进行了系统的仿真和试验研究。文献[1-2]根据弹性滚子接触模型和台架试验对考虑滤波效应的有效路形和轮胎包容的特点与规律进行了系统分析，并基于环模型理论进一步对轮胎低速稳态包容特性进行了仿真分析和试验验证。文献[3-6]基于试验模态参数建立了轮胎的静垂直特性模型，对轮胎的包容特性进行了定量分析，并根据固定轴高和固定垂直轴荷的试验方法对其分析结果进行了试验验证。Alkan等[7-8]对轮胎的径向刚度和包容特性进行了仿真和试验研究，并定量分析了车轮包容特性的影响因素。

在前期研究的基础上[9-10]，基于有限元分析和试验测试方法，笔者对机械弹性车轮在不同障碍物作用下的垂向力学特性和低速稳态包容特性进行分析，并研究车轮通过障碍物后的垂向和纵向动态力学响应的变化规律，及负荷和障碍物截面形状对包容特性的影响，为车轮结构优化设计及整车动力学特性的研究提供参考。

1 车轮结构与包容特性分析

1.1 机械弹性车轮结构

新型机械弹性车轮主要由輮轮(橡胶胎圈、弹性钢丝环、卡环)、轮毂、销轴及铰链组等部件构成，结构如图1所示。

图1 机械弹性车轮结构Fig.1 Structure of mechanical elastic wheel

机械弹性车轮工作过程中，车轴传给轮毂的垂直载荷与扭矩使得铰链组由平衡状态变为预紧状态，进而拉动輮轮产生拉力，该力沿车轮外圆的切向分力克服车轮与地面的静摩擦力，使得车轮滚动。由于轮毂依靠铰链组的拉力悬挂于輮轮内，当受垂直载荷影响时，轮毂相对于自由状态向下移动一段距离，位于轮毂距地面较近区域的铰链组不受力呈微曲状，輮轮上部因受到轮毂向下的拉力，使其具有一定范畴内的类椭圆弹性变形；当车轮滚动时，来自路面的激励，大部分将为輮轮所承受，并瞬时随其弹性变形和相应铰链组的瞬时弯曲所缓解，故该车轮具有不同于普通充气轮胎的缓冲减振性能[11]。

1.2 包容特性分析

当轮胎在不平路面上滚动时，路面的垂直扰动输入并不是真实路形，而是由轮胎垂直弹性和几何尺寸滤波后的有效路形，表征轮胎包容特性的系统可用四端网格来表示，如图2所示。

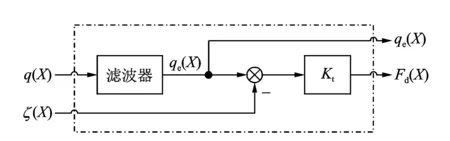
图2 轮胎包容特性模型Fig.2 Tire enveloping characteristics model

图中：q(X)为真实路形；qe(X)为滤波后的有效路形；ζ(X)为轮心的垂直位移；Kt为轮胎的垂直刚度；Fd(X)为路面对轮胎的动态垂直作用力；X为轮胎纵向滚动距离；滤波器为轮胎的滤波效应。

建立轮胎包容特性模型就是确定Fd(X)或qe(X)与q(X)之间的数学关系，即为

(1)

当轮胎低速直线滚动时，其轮心的垂直位移ζ(X)就是有效路形，即：qe(X)=ζ(X)。针对新型机械弹性车轮的整体结构，鉴于輮轮橡胶体和弹性钢丝环的双重迟滞作用，使其车轮具有更加良好的包容凸块、减小冲击和延长作用时间的特性。

2 机械弹性车轮有限元模型的建立

机械弹性车轮的輮轮主要由橡胶体、帘布、弹性钢丝环等多种材料构成，如图3所示。輮轮中的胎胶层、帘布层、弹性钢丝环层等结构组份材料的分布决定机械弹性车轮不同的刚度特性，为了尽可能准确地模拟车轮性能，需要对輮轮结构的复合材料进行力学性能研究[12]。

图3 层合结构模型Fig.3 Laminated structure model

輮轮中的帘布复合材料属于三维正交各向异性复合材料，具有近似体积不可压缩性和非线性的本构关系。初始构型中，帘线的方向向量和基体的法向向量相同，为了较好地表征橡胶材料力学特性，通常采用Mooney-Rivlin超弹性本构模型进行描述，其应变能函数W是变形张量不变量(I1,I2,I3)的函数，即W=W(I1,I2,I3)，橡胶又为不可压缩性材料，即I3=1，则应变能函数模型为

(2)

其中：I1，I2为左Cauchy-Green变形张量中的第1和2基本不变量；Cij为材料参数。

则有

(3)

(4)

其中：I1，I2，I3为二阶张量不变量，下角标1，2和3表示3个相互垂直的方向。

材料只有单方向拉伸，则有：λ1λ2λ3=1。

对于輮轮的橡胶材料，∂W/∂I2远远小于∂W/∂I1，且近似为零，故有Yeoh模型为

W=C10(I1-3)+C20(I1-3)2+C30(I1-3)3

(5)

Yeoh模型能够充分地描述橡胶-帘布复合材料的性能，并且仅可由单轴拉伸试验确定其材料参数。采用Instron公司万能拉伸测试仪对輮轮橡胶体材料进行单向拉伸试验，试样取件为胎面层和胎内层等橡胶-帘布复合材料。通过对单向拉伸应力-应变测试结果的分析，可得Yeoh模型的材料参数，如表1所示。机械弹性车轮不同组件的材料性能参数如表2所示。

表1 胶料Yeoh模型材料参数

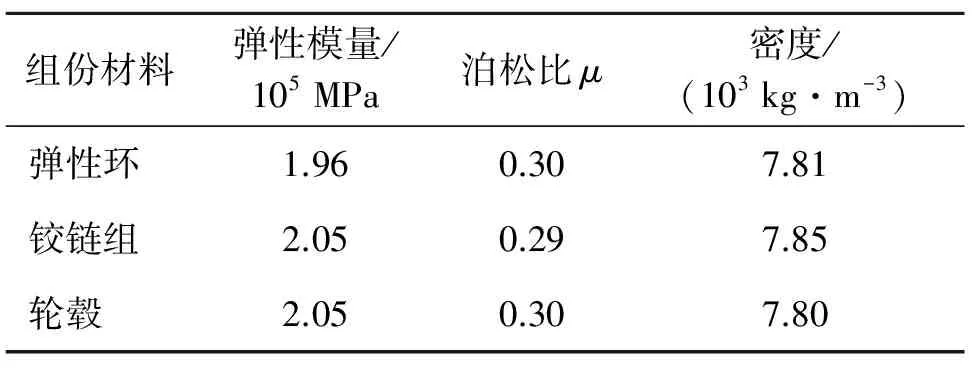
表2 机械弹性车轮各部件材料性能参数

将机械弹性车轮模型进行适当的简化，忽略车轮花纹和轮毂形状对分析的影响，将铰链组简化为12组沿輮轮周向均匀分布的三节连杆结构，使用Pro/E建立輮轮、铰链组、轮毂等三维几何模型，并将几何模型导入有限元分析软件ABAQUS中。采用rebar单元模拟帘布-橡胶复合材料的性能，并采用C3D10M单元分别对橡胶体、弹性钢丝环、铰链组及轮毂进行网格划分，根据各部件材料性能参数对其赋值，生成的车轮三维有限元模型如图4所示。

图4 车轮与障碍物有限元模型Fig.4 Finite element model of wheel and cleats

在机械弹性车轮垂向承载过程中，车轮和接触面之间的变形属于大变形非线性的接触问题，为防止接触节点之间的穿透，地面采用刚性墙进行模拟。在静态分析过程中，将台面固定不动，施加垂向载荷使车轮产生变形；准静态分析过程中，施加一定预载荷使车轮产生垂向变形，并使车轮以某一速度水平移动。

3 车轮垂向刚度特性分析

不同条件下的垂向刚度是影响车轮包容特性的重要参数。为验证路面不平度对车轮垂向刚度的影响，利用轮胎加载变形测试试验和有限元分析方法，对平面及障碍物作用下机械弹性车轮的垂向刚度特性进行研究。在试验过程中，将障碍物移至轮心正下方，采用静态差量加载法对其车轮的垂向刚度特性进行测试[13-15]。由于橡胶材料和弹性钢丝环的迟滞作用，为准确表达车轮的静刚度特性进行多次试验，取加、卸载变形的均值来表示车轮的静刚度特性。

在平面情况下，对车轮垂向刚度进行测试。由图5可知，有限元模型的负荷特性曲线与静态加载试验值具有较好的一致性，验证了所建模型的可靠性，表明该有限元模型可用于车轮包容特性的进一步研究。

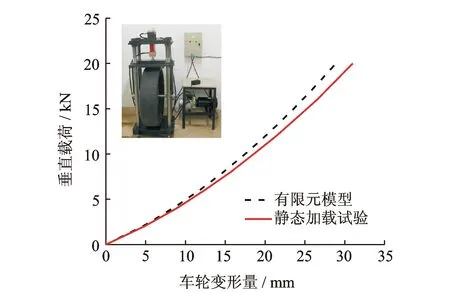
图5 试验结果与有限元计算的负荷特性对比Fig.5 Comparison of experimental results with finite element calculation of load characteristics

在相同加载条件下，将矩形1截面(高为10 mm，宽为20 mm)、矩形2截面(高为15 mm，宽为20 mm)和三角形截面(高为15 mm，底部宽为30 mm)的障碍物分别移至车轮轮心正下方，利用有限元分析方法和加载变形试验，对不同障碍物作用下的车轮垂向力学特性进行分析，车轮垂向载荷与变形量之间的关系如图6所示。

图6 车轮垂向刚度曲线Fig.6 Vertical stiffness curve of wheel

分析加载载荷和车轮变形量之间的关系时，选取台面基础表面为参考平面，设车轮胎面与台面接触时的车轮变形量为“0”。通过上述数据分析可知，由于障碍物截面形状的不同，当加载载荷达到某一定值时，车轮垂向位移才从零开始变化。由图6(a)和6(b)对比可知，垂向位移的初始加载值随障碍物高度的增加而增大；由图6(b)和6(c)对比可知，在障碍物高度相同的情况下，所产生的垂向刚度随障碍物截面形状的不同而变化。

为更有效地验证车轮的静态包容特性，根据车轮关于中心平面对称，将三角形障碍物移至距车轮轴心66.5和133 mm处进行分析，试验结果如图7所示。

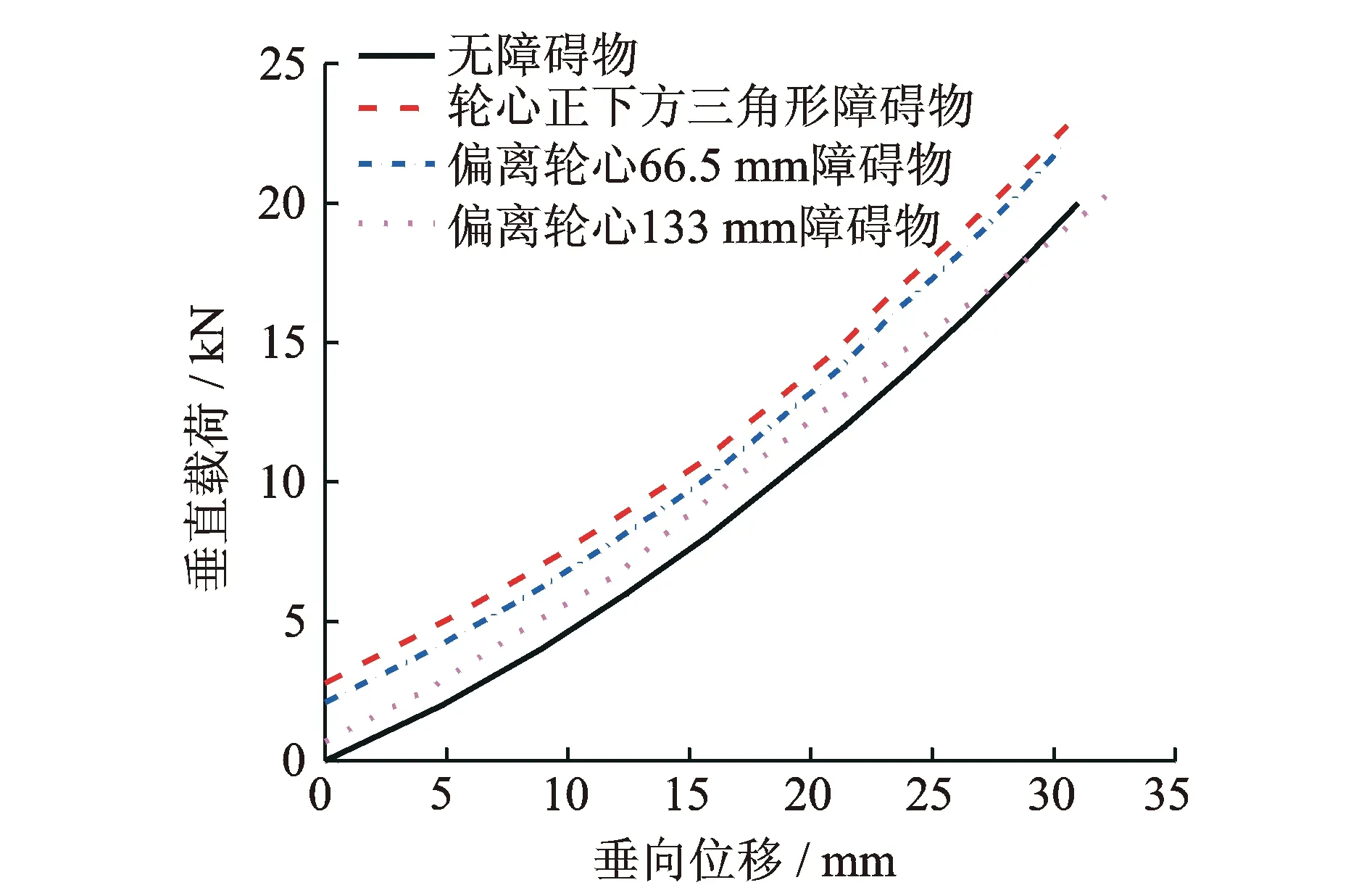
图7 三角形障碍物不同位置下的车轮垂向刚度Fig.7 Vertical stiffness of wheel in different position of triangular obstacles

由图7可知，垂向刚度随障碍物距轮心的位移而发生变化，但位于车轮轮心两侧相同位置的垂向刚度是相等的，从而说明了车轮具有较好的对称包容特性。在有限元建模时，材料模型没有考虑能量的耗散，以致有限元计算和试验测试存在较小差异，但有限元计算与试验测试结果整体具有较好的一致性，表明了所建模型的有效性。基于车轮有限元分析和加载试验，在某一载荷条件下，位于车轮轮心下方的障碍物被车轮完全包容，表现出车轮典型的静包容特性。

4 车轮包容特性力学分析

车轮与路面的接触是一个面接触的过程，路面的凹凸不平程度决定着车轮的刚度沿垂向或纵向是不均等的，而车轮负荷和障碍物横截面尺寸及形状是影响车轮包容力学特性的主要参数。自主研发的平板式多功能轮胎试验台结构如图8所示。试验台轴头在液压机构控制下只作上下移动，障碍物凸块固定于试验台面上随台面移动，在保持轴头高度不变的情况下，对车轮进行固定载荷的包容特性试验。

图8 多功能轮胎试验台Fig.8 Tire multifunctional testbed

设置台面匀速移动的速度为0.02 m/s，试验工况如表3所示，通过力和位移传感器可测得轴头的垂向力和纵向力，及轴头垂直位移和试验台面的水平位移，通过数据显示仪记录数据。

表3 机械弹性车轮包容特性试验工况

Tab.3 Experimental conditions of mechanical elastic wheel enveloping

凸块截面形状/mm载荷/N与车轮中心面的夹角/(°)矩形1(10×20)370090矩形2(15×20)510090三角形(15×30)680090

4.1 车轮垂向力响应分析

当车轮滚过不同截面障碍物时，通过有限元计算和台架试验可知，车轮垂向力响应随移动位置的变化而变化，如图9所示，当垂直载荷(3 700 N)较小时，车轮垂向力变化曲线只有一个最大值；随垂直载荷达到某一值(5 100 N)时，曲线中间出现下榻，变成马鞍形；进一步加大载荷，当载荷为6 800 N时，轮心变化曲线在中间部分略有升高，处于障碍物正下方的车轮轮心高度接近于在水平台面上的值，这种现象称为典型的包容特性。

图9 车轮垂向力变化曲线Fig.9 Variation curve of wheel vertical force

通过上述分析可知，有限元计算结果和试验值吻合较好，但由于有限元模型的垂直刚度比试验值偏高，所以计算的垂向力值比试验值也略高，误差基本在5%以内，从而表明了所建有限元模型的正确性。由图9(a)和9(b)对比分析可知，垂向力值随障碍物高度的增加而增大，鉴于车轮下沉量，随障碍物高度的增加，垂向力较快达到最大值；由图9(b)和9(c)对比，在障碍物高度相同的情况下，所产生的垂向力随障碍物截面形状的不同而变化，但都表现出良好的车轮包容特性。

4.2 车轮纵向力响应分析

通过有限元计算和台架试验可知，车轮纵向作用力仿真值和试验值基本保持一致，变化曲线类似为正弦曲线形状，如图10所示。在轮心处于障碍物正上方处，纵向作用力接近为零，且纵向作用力被分为左右两部分，出现了一个负的和正的最大值，从而说明所产生的纵向作用力对车轮越障特性起到决定作用。

图10 车轮纵向力变化曲线Fig.10 Variation curve of wheel longitudinal force

通过上述数据分析可知，当车轮位于试验平台面和障碍物正上方时，纵向作用力基本为零，出现的较小偏差是由车轮自身锥度效应所产生的。纵向力响应随障碍物高度的增加而增大，且障碍物截面形状的不同对其变化规律和大小都有影响。

综上所述，负荷的增加对车轮垂向作用力的影响比对纵向作用力的影响更加显著。在相同负荷(5 100 N)条件下，车轮通过矩形1截面、矩形2截面和三角形截面三种障碍物的最大垂向力分别为6 135,6 514和6 306 N，最大纵向力分别为447.5,769.3和589.3 N。对比分析可得，车轮垂向力和纵向力响应随障碍物高度的增加而增大，而障碍物截面形状的不同对其变化规律和大小都有影响。根据对比并得出垂向力和纵向力响应峰值相对较低，变化较平缓，车轮表现出良好的包容性能。

5 结束语

通过有限元计算和车轮加载试验分析可知，有限元模型的负荷特性曲线与静态加载试验值具有较好的一致性，验证了所建模型的可靠性。位于车轮正下方的障碍物截面尺寸和形状不同时，产生的垂向位移初始加载值随障碍物高度的增加而增大，随形状的不同而变化；垂向刚度随障碍物距轮心的位移而发生变化，但位于车轮轮心两侧相同位置的垂向刚度是相等的。

车轮越过三种障碍物后的垂向力学响应具有相似的变化规律，随负荷的增加由抛物线形过渡到马鞍形；车轮纵向动态力学响应随负荷的增加而增大，其变化曲线类似为正弦形状；且车轮垂向力和纵向力响应随障碍物高度的增加而增大。在一定载荷条件下，位于车轮轴心下方的障碍物被车轮完全包容，表现出典型的包容特性，根据对比得出垂向力和纵向力响应峰值相对较低，变化较平缓，表明了该车轮具有良好的包容性能。

[1] 郭孔辉，刘青，丁国峰.轮胎包容特性分析及其在汽车振动系统建模中的应用[J].汽车工程，1999，21(2)：65-71.

Guo Konghui, Liu Qing, Ding Guofeng. Analysis of tire enveloping properties and its application in modeling of vehicle vibration systems[J]. Automotive Engineering, 1999,21(2):65-71. (in Chinese)

[2] 邱恩超，郭孔辉.基于环模型的轮胎有限元建模与仿真研究[J].汽车技术，2009(7)：4-9.

Qiu Enchao, Guo Konghui. Tire FE modeling based on circle model and simulation study [J]. Automobile Technology, 2009(7):4-9. (in Chinese)

[3] 安宏伟，管迪华，范成建.轮胎静包容特性的试验研究[J].汽车工程，2004，26(1)：57-60.

An Hongwei, Guan Dihua, Fan Chengjian. An experimental study on tire static enveloping properties[J]. Automotive Engineering, 2004,26(1):57-60. (in Chinese)

[4] 范成建，管迪华.利用试验模态参数对轮胎包容特性的建模及试验验证[J].汽车工程，2006，28(2)：138-142.

Fan Chengjian, Guan Dihua. Modeling and experimental verify cation of tire enveloping properties using experimental modal parameters[J]. Automotive Engineering, 2006,28(2):138-142. (in Chinese)

[5] Guan Dihua, Fan Chengjian, Xie Xianhai. A dynamic tyre model of vertical performance rolling over cleats[J]. Vehicle System Dynamics, 2005,43(1):209-222.

[6] 管迪华，范成建.用于不平路面车辆动力学仿真的轮胎模型综述[J].汽车工程，2004，26(2)：162-167.

Guan Dihua, Fan Chengjian. A review of tire models for vehicle dynamics simulation on uneven road[J]. Automotive Engineering, 2004,26(2):162-167. (in Chinese)

[7] Alkan V, Karamihas S M, Anlas G. Experimental analysis of tyre-enveloping characteristics at low speed[J]. Vehicle System Dynamics, 2009,47(5):575-587.

[8] Alkan V, Karamihas S M, Anlas G. Finite element modeling of static tire enveloping characteristics[J]. International Journal of Automotive Technology, 2011,12(4):529-535.

[9] Li Bo, Zhao Youqun, Zang Liguo. Closed-form solution of curved beam model of elastic mechanical wheel[J]. Journal of Vibroengineering, 2014,16(8):3951-3962.

[10]臧利国，赵又群，李波，等.非充气机械弹性安全车轮静态径刚度特性研究[J].兵工学报，2015，36(2)：354-362.

Zang Liguo, Zhao Youqun, Li Bo, et al. Static radical stiffness characteristics of non-pneumatic mechanical elastic wheel[J]. Acta Armamentarii, 2015,36(2):354-362. (in Chinese)

[11]汪伟，赵又群，姜成，等.新型机械弹性车轮的力学传递特性分析[J].江苏大学学报：自然科学版，2013，34(3)：261-266.

Wang Wei, Zhao Youqun, Jiang Cheng, et al. Characteristics analysis of mechanical transmission for a new mechanical elastic wheel [J]. Journal of Jiangsu University ：Natural Science Edition, 2013,34(3):261-266. (in Chinese)

[12]程钢.子午线轮胎力学行为仿真及试验方法研究[D].济南:山东大学,2005.

[13]Wang Wei, Yan Shan, Zhao Shugao. Experimental verification and finite element modeling of radial truck tire under static loading[J]. Journal of Reinforced Plastics and Composites, 2013,32(7):490-498.

[14]Tae K L, Byoung S K. Vibration analysis of automobile tire due to bump impact[J]. Applied Acoustics, 2008,69(6):473-478.

[15]Kang N. Prediction of tire natural frequency with consideration of the enveloping property[J]. International Journal of Automotive Technology, 2009,10(1):65-71.

*总装备部探索研究重大资助项目(NHA13002)；江苏省普通高校研究生科研创新计划资助项目(KYLX-0241)；中央高校基本科研业务费专项资金资助项目(NS2015015)

2016-01-03；

2016-05-10

10.16450/j.cnki.issn.1004-6801.2017.02.009

U463.3； TH114

王强，男，1985年4月生，博士生。主要研究方向为汽车动态仿真与控制。曾发表《Equivalent stiffness and dynamic response of new mechanical elastic wheel》(《Journal of Vibroengineering》2016，Vol.18,No.1)等论文。 E-mail:wqyp2014@163.com