扫描隧道显微镜扫描器的迟滞非线性控制*

季宏丽, 孙宏君, 裘进浩, 陈远晟, 朱孔军

(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016) (2.南京理工大学能源与动力工程学院 南京,210094)



扫描隧道显微镜扫描器的迟滞非线性控制*

季宏丽1, 孙宏君1, 裘进浩1, 陈远晟2, 朱孔军1

(1.南京航空航天大学机械结构力学及控制国家重点实验室 南京，210016) (2.南京理工大学能源与动力工程学院 南京,210094)

压电驱动器被广泛应用于扫描隧道显微镜(scanning tunneling microscope,简称STM)的扫描器，但压电材料本身的迟滞非线性特性影响了STM的扫描精度。为了补偿由于迟滞非线性带来的扫描器控制误差，提高STM的扫描精度，基于迟滞非线性模型，设计了前馈控制器，并与PID反馈控制相结合。利用所设计的控制器进行了扫描实验，并与位移反馈控制扫描进行对比。实验结果表明，采用位移反馈控制时光栅周期相对测量误差和光栅线宽相对测量误差分别为4.41%和2.65%，采用迟滞逆模型与PID反馈的复合控制后，光栅周期相对测量误差和光栅线宽相对测量误差分别减小到1.26%和0.27%，迟滞引起的非线性误差得到了补偿，减小了扫描器控制误差，提高了扫描精度。

扫描隧道显微镜； 压电驱动器； 迟滞控制； 扫描控制

引 言

STM作为研究纳米技术等当今前沿科技领域的主要工具而备受重视。STM的基本工作原理是在探针和被测样品表面加上偏压，当探针尖与样品之间产生隧道电流时，通过对隧道电流的检测得到样品的表面信息。STM在扫描过程中要求扫描器的位移精度高，响应速度快，所以其扫描器大多采用压电驱动器。这种驱动器具有响应速度快，功耗低，不需传动机构等特点，但压电驱动器本身所具有的迟滞特性，很大程度上影响了STM的扫描精度。目前大多数STM的扫描器采用位移反馈的方法减小控制误差，提高扫描精度。Abramovitch等[1]设计了PID参数自调整的方法代替手动调节，用于STM的扫描器控制。Mahmood等[2]设计了一种正位置反馈的方法，与PI控制器结合使用对STM的扫描器进行控制，得到了很好的结果。杨学恒等[3]设计了积分比例调节用于STM的扫描器控制。这些方法的优点是可以减小控制误差， 获得较准确的扫描结果，但其补偿信息中不包括对应的迟滞特性[4]，因而不能准确地针对迟滞特性进行补偿，而且为了得到更好的控制效果，有时需要很高的反馈系数，但是过高的反馈系数容易导致系统失稳[5]。文献[6-9]设计了基于迟滞逆模型的控制器，将其应用于压电驱动器的控制中。目前被用于描述压电驱动器迟滞非线性现象的模型，根据其建模原理，可分为物理模型和现象模型两类。其中，现象模型是用尽量精确的数学模型描述压电驱动器输入与输出的关系而不考虑迟滞现象发生的物理成因，因此方便建模并易于控制器设计。Song等[6]针对压电双晶片的迟滞问题，基于Preisach模型逆模型设计了跟踪控制器，减小了控制误差。Ang等[7]基于PI模型逆模型设计了相应的控制器，成功地补偿了压电驱动器的迟滞非线性问题。针对压电驱动器与直流电机的复合微定位平台的迟滞问题，Juhász等[8]基于Maxwell模型设计了控制器，提高了控制精度。Jiang等[9]针对PI模型不能描述非对称迟滞现象的问题设计了改进模型，解决了PI模型非对称建模的问题。文献[10-11]建立了动态迟滞模型, 获得了较好的控制效果。

本研究将迟滞逆模型控制应用于STM的扫描器控制系统中，补偿扫描器的迟滞，并且通过与PID反馈结合的复合控制，进一步减小控制误差，得到了较准确的扫描结果。与位移反馈控制相比，利用迟滞逆模型与PID反馈复合控制的方法补偿扫描器的迟滞特性，控制更加精确，不会产生因反馈系数过大而使系统失稳的情况，且可用于大范围扫描控制。

1 STM控制系统

1.1 工作原理

STM控制系统工作过程分为：a．隧道电流搜索控制；b．扫描控制。隧道电流搜索控制，控制系统驱动粗调定位机构使样品逼近探针针尖，并通过与竖直方向的扫描器配合使样品进入隧道区，保持隧道电流稳定。扫描控制阶段，控制系统驱动STM的扫描器进行竖直方向上的间距保持和水平方向上的扫描轨迹跟踪。扫描轨迹跟踪如图1所示，控制过程如图2所示。

图1 水平方向上的扫描轨迹跟踪示意图Fig.1 Diagram of scanning track in horizontal direction

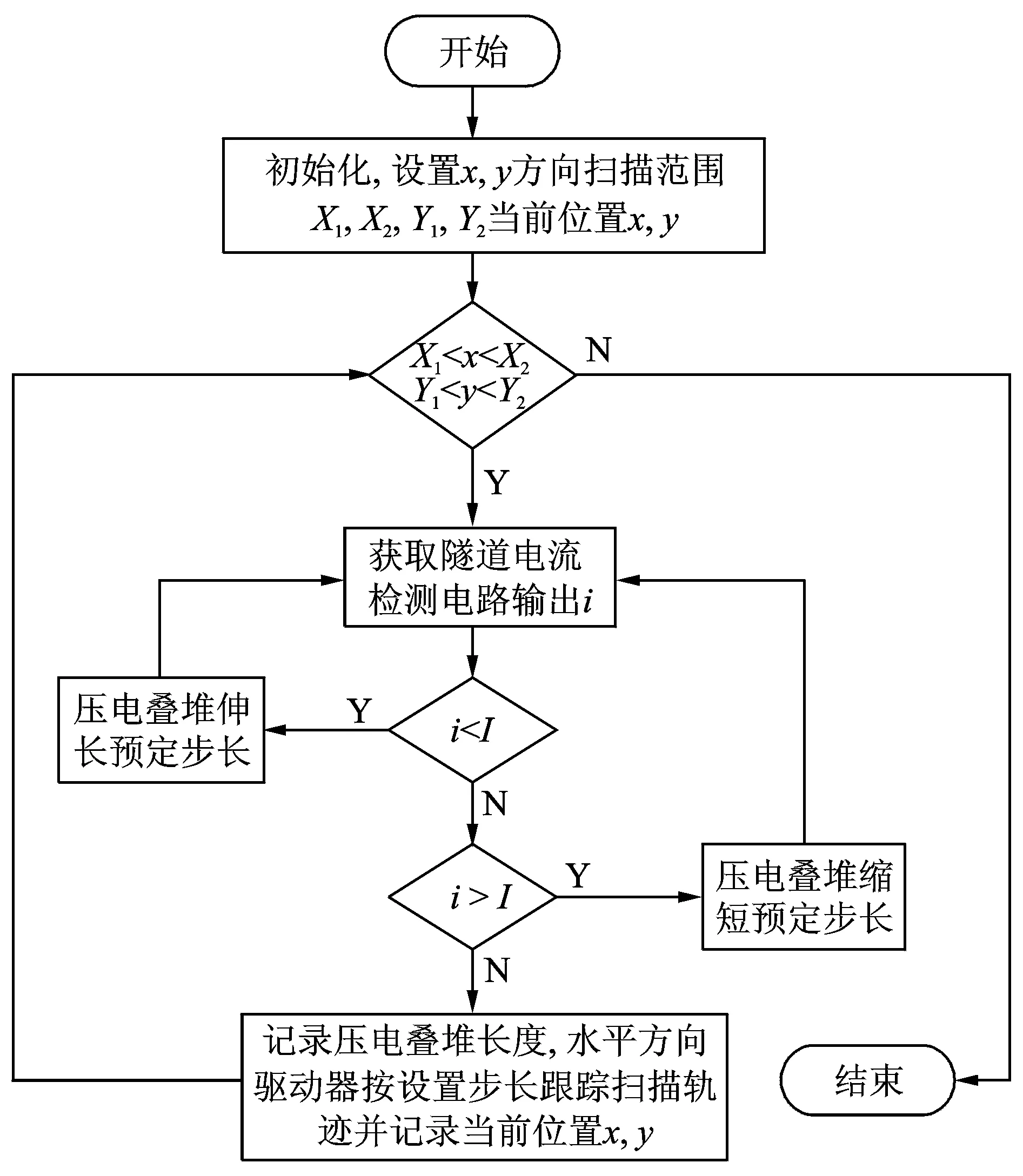
图2 扫描控制流程图Fig.2 Flow chart of scanning control

STM的扫描器采用压电驱动器, 压电驱动器本身具有迟滞非线性特性。压电驱动器的迟滞特性表现为输入电压与输出位移之间的非线性关系，升压降压位移曲线有明显的位移差，如图3所示[12]。

图3 输入电压与位移关系的迟滞特性Fig.3 Hysteresis property between input voltage and displacement

当STM检测样品表面起伏时，在水平面内，x方向上的扫描电压信号采用正弦信号，y方向的扫描电压信号采用上升信号。结合图1可知，扫描过程中主要依靠x方向扫描器的连续移动得到各点的起伏状态，因此，x方向扫描器的迟滞问题会导致扫描结果有较大的误差。所以，将迟滞逆模型控制及其与PID反馈的复合控制加入到x方向扫描器的控制中，用以解决其迟滞非线性问题。

1.2 基于迟滞模型的微位移控制

压电驱动器迟滞逆模型控制原理如图4所示，期望位移信号通过迟滞逆模型时，计算出相应的输出电压，该电压加到压电驱动器上，压电驱动器会产生相应的位移。期望位移信号与输出电压信号，输出电压信号与输出位移信号间均存在迟滞关系，但是期望位移与输出位移间是线性关系。

图4 迟滞逆模型控制原理Fig.4 Principal of inverse model control

迟滞逆模型控制结构简单，在理想条件下能够有效减小压电驱动器的迟滞非线性现象，提高控制精度。为进一步提高控制精度，引进PID反馈与迟滞逆模型控制相结合，形成复合控制。

迟滞逆模型与PID反馈的复合控制原理如图5所示[4]。在迟滞逆模型控制的基础上增加一个反馈支路，该支路通过PID控制器补偿由于外界干扰等带来的误差。

图5 迟滞逆模型与PID复合控制原理Fig.5 Compound control of inverse hysteresis model and PID controller

Maxwell迟滞模型是用摩擦力和弹簧系统描述具有迟滞特性的位移与力的关系[13]。Maxwell模型是由多个被称作弹性滑动单元(见图6)的基础单元并联叠加构成[13]，如图7所示。系统的表达式[13]为

(1)

(2)

其中：F为总输出力；Fi为第i个弹性滑动单元的输出力；n为弹性滑动单元个数；ki为第i个弹性滑动单元弹簧的刚度系数；x为输入位移；fi=μNi为第i个弹性滑动单元物块运动时需要克服的摩擦力；xbi为第i个弹性滑动单元物块的位移。

图6 弹性滑动单元 图7 Maxwell模型Fig.6 Elasto-slide element Fig.7 Maxwell model

与其他迟滞模型相比，Maxwell模型的各弹簧之间是并联的，而且弹性滑动单元没有质量，因此增加弹性滑动单元的数目便可提高模型的精度，并且不增加模型的阶数[14]。但Maxwell模型的缺点是只能描述对称的迟滞现象。而常用的压电驱动器所具有的迟滞特性都是非对称的，针对Maxwell迟滞模型不能描述非对称迟滞特性的问题，文献[4]对弹性滑动单元进行了改进，将弹性滑动单元由原来上升段和下降段特性相同的单元，转变为上升段和下降段特性不同的新单元[4]，如图8所示，其表达式为增量式[4]

Fi(kT)=

(3)

这种改进的Maxwell模型具有经典Maxwell模型的所有优点, 同时可以描述经典Maxwell模型无法描述的非对称迟滞特性。利用改进的Maxwell模型设计迟滞逆模型控制器，用于STM的x方向扫描器控制。改进的Maxwell模型仍然是一种现象模型，其数学表达式仅描述压电驱动器输入与输出的关系而不考虑迟滞现象发生的物理成因，所以其逆模型与正模型可以有相同的形式。为了获得逆模型的参数，仅需要将迟滞特性数据的输出位移作为逆模型的输入，将输入电压作为逆模型的输出进行辨识即可[15-16]。

图8 改进后的弹性滑动单元Fig.8 Modified elasto-slide element

2 实验与分析

2.1 实验系统搭建

笔者设计了用于实验的STM硬件系统，主要由驱动机构、钨探针、前置放大电路、工控机与dSPACE系统以及隔振平台组成。

驱动机构包含粗调定位用驱动器与精密定位用扫描器。竖直方向的粗调定位用驱动器采用电动升降台，其行程为50 mm，分辨率0.019 5 μm。水平方向的粗调定位用驱动器采用手动位移台，其行程为50 mm，最小调整量2 μm。另外，为了尽量保持探针与样品之间的垂直度，选用了手动倾斜台，调整范围±4°，最小调整量5′。 精密定位用扫描器采用压电驱动器。竖直方向扫描器采用压电叠堆，行程13 μm，分辨率0.13 nm。 水平方向驱动器采用美国Npoint公司的XY100A型纳米位移平台，行程100 μm，内置电容位移传感器。

STM主要是通过检测探针尖与样品表面距离足够小时产生的隧道电流来工作的，因此探针的制备非常关键。作为一项比较成熟的技术，本研究采用了电化学腐蚀法制备钨探针[17-19]，制备的探针经扫描电镜检测符合要求。前置放大电路的作用是将极其微弱的隧道电流信号转换成较大的，可检测的电压信号[20]。本研究采用的是两级放大，即基本前置放大电路后接一个电压放大电路。电路的电流电压转换系数为0.2 V/nA。

实验样品为一维导电光栅，使用扫描电子显微镜(SEM)对样品进行观察，如图9所示，样品的周期与线宽均匀。通过局部放大的图像如图10所示，取一个周期进行观测，光栅周期为20.64 μm， 线宽为11.32 μm(在下面的STM扫描实验分析中认为该数据为真实值)。

图9 SEM扫描图像Fig.9 SEM scanned image

图10 SEM局部扫描图像Fig.10 SEM partial scanned image

扫描范围设定为60.00 μm×60.00 μm. 扫描预设采样率为2.5 kHz，x方向扫描器的控制频率为0.1 Hz。STM作为一种精密仪器，虽然已经对其进行了隔振等处理，但是外界的任何扰动仍然可能使已经进入隧道区的探针在当前时刻脱离隧道区，这时采集到的信号不准确。尤其在大范围扫描时，保证在每个采样点都能得到稳定的隧道电流是非常重要的。因此，笔者设计了竖直方向间距保持和水平方向扫描轨迹跟踪的联动控制，即如果在扫描过程中探针尖脱离隧道区，水平方向扫描器会保持在当前位置，当竖直方向扫描器驱动探针重新进入隧道区后，水平方向扫描器继续跟踪扫描轨迹，所以实验中的x方向扫描器的频率会略低于0.1 Hz。得到原始信号中含有高频噪声干扰，通常情况下可以使用低通滤波或小波去噪的方法进行处理，但是扫描光栅信号中有突变成分，为了在去掉噪声的同时保留信号的有用成分，本研究采用小波去噪。

2.2 电压控制扫描

取一个周期的扫描结果，如图11所示。一个扫描周期内，光栅平均周期和平均线宽分别为23.22和12.87 μm；沿x正方向扫描时，光栅平均周期和平均线宽分别为25.28和14.00 μm；沿x负方向扫描时，光栅平均周期和平均线宽分别为21.15和11.73 μm。一个扫描周期内，光栅周期和线宽相对测量误差(相对测量误差=(测量值-真实值)/真实值)分别为12.50%和13.69%；沿x正向扫描时，光栅周期和线宽相对测量误差分别为22.48%和23.67%；沿x负向扫描时，光栅周期和线宽相对测量误差分别为19.32%和3.62%。

图11 电压控制扫描结果Fig.11 Result of voltage controlled scanning

2.3 位移反馈控制扫描

将位移信号作为反馈量，利用PID控制器进行位移反馈控制。取一个周期的扫描结果，如图12所示。一个扫描周期内，光栅平均周期和平均线宽分别为19.73和11.02 μm；沿x正方向扫描时，光栅平均周期和平均线宽分别为19.65和10.94 μm；沿x负方向扫描时，光栅平均周期和平均线宽分别为19.82和11.09 μm。一个扫描周期内，光栅周期和线宽相对测量误差分别为4.41%和2.65%；沿x正向扫描时，光栅周期和线宽相对测量误差分别为4.80%和3.36%；沿x负向扫描时，光栅周期和线宽相对测量误差分别为3.97%和2.07%。

图12 位移反馈控制扫描结果Fig.12 Scanning results with displacement feedback control

2.4 迟滞逆模型控制扫描

取一个周期的扫描结果，如图13所示。一个扫描周期内，光栅平均周期和平均线宽分别为19.96和11.20 μm；沿x正方向扫描,光栅平均周期和平均线宽分别为19.94和11.17 μm；沿x负方向扫描，光栅平均周期和平均线宽分别为19.98和11.22 μm。一个扫描周期内，光栅周期和线宽相对测量误差分别为3.29%和1.06%；沿x正向扫描时，光栅周期和线宽相对测量误差分别为3.39%和1.33%；沿x负向扫描时，光栅周期和线宽相对测量误差分别为3.20%和0.88%。

图13 迟滞逆模型控制扫描结果Fig.13 Result of tracking control with inverse hysteresis model

2.5 迟滞逆模型与PID复合控制扫描

取一个周期的扫描结果，如图14所示。一个扫描周期内，光栅平均周期和平均线宽分别为20.38和11.35 μm；沿x正方向扫描，光栅平均周期和平均线宽分别为20.35和11.42 μm，沿x负方向扫描，光栅平均周期和平均线宽分别为20.40和11.28 μm。一个扫描周期内，光栅周期和线宽相对测量误差分别为1.26%和0.27%；沿x正向扫描时，光栅周期和线宽相对测量误差分别为1.41%和0.88%，沿x负向扫描时，光栅周期和线宽相对测量误差分别为1.16%和0.35%。

图14 迟滞逆模型与PID复合控制扫描结果Fig.14 Result of tracking control with inverse hysteresis model

2.6 扫描结果分析

三种控制条件下的x方向扫描器跟踪误差，实际位移与期望位移关系如图15所示。

如图15(a)所示，单独电控制时，x方向扫描器在控制前其定位精度不高，最大跟踪误差(跟踪误差=期望位移-实际位移)达到了6.78 μm，均方根误差为3.08 μm，而且沿x负方向运动时误差更大。从迟滞曲线上可以看出，驱动器迟滞现象明显，且迟滞曲线呈不对称性。所以单独电压控制扫描时得到的扫描结果误差很大，且正负两个方向扫描时结果相差较大，如图11所示。

如图15(b)所示，位移反馈控制时，最大跟踪误差减小到0.99 μm，均方根减小到0.28 μm。其控制误差明显减小，所以其扫描精度比单独电压控制时有显著提高。但是对扫描器迟滞非线性的控制效果不够理想，尤其在位移两端的位置，有明显的迟滞现象。

如图15(c)所示，x方向扫描器加入迟滞模型控制后，其控制误差也明显减小，最大跟踪误差减小到0.45 μm，均方根误差减小到0.15 μm。相比于位移反馈控制，对迟滞现象控制效果明显变好。所以其扫描效果较位移反馈控制时有明显改善。

如图15(d)所示，x方向驱动器加入迟滞逆模型与PID结合的闭环控制后，其控制误差进一步减小，最大跟踪误差减小到0.09 μm，均方根误差减小到0.02 μm，迟滞现象基本得到补偿。所以其扫描精度比位移反馈控制和迟滞逆模型前馈控制时有很大提高。

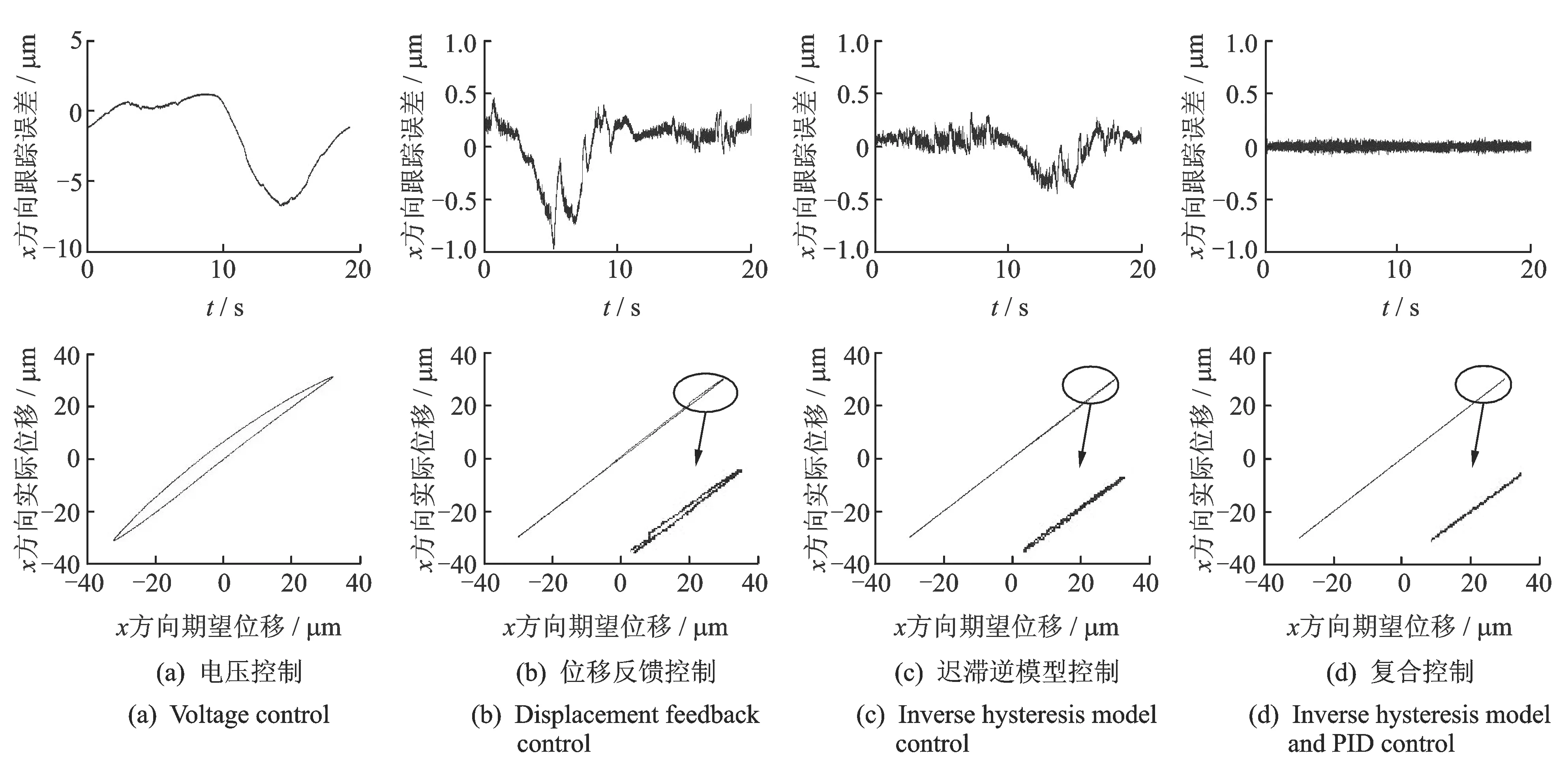
图15 不同控制条件下的扫描器跟踪误差、实际位移与期望位移关系Fig.15 Tracking error, relationship between desired and actual displacement of scanning stage in different control conditions

3 结束语

压电驱动器因具有响应速度快、功耗低、不需传动机构等特点而被用作STM扫描器。但压电驱动器所具有的迟滞非线性特性，很大程度上影响了STM的扫描精度，本研究将迟滞逆模型控制用于STM扫描器控制系统中，并最终通过迟滞逆模型与PID复合控制，使光栅周期相对测量误差由位移反馈控制的4.41%降低到1.26%，线宽相对测量误差由2.65%降低到0.27%。迟滞获得补偿，得到了较为准确的扫描结果。

[1] Abramovitch D Y, Hoen S, Workman R. Semi‐automatic tuning of PID gains for atomic force microscopes[J]. Asian Journal of Control, 2009,11(2):188-195.

[2] Mahmood I A, Moheimani S O R. Making a commercial atomic force microscope more accurate and faster using positive position feedback control[J]. Review of Scientific Instruments, 2009,80(6):063705.

[3] 杨学恒, 陈安, 何光宏,等. 扫描隧道显微镜系统[J]. 重庆大学学报：自然科学版, 2001,24(3):137-141.

Yang Xueheng, Chen An, He Guanghong, et al. System of scanning tunneling microscope[J]. JournaI of Chongqing University：NaturaI Science Edition, 2001,24(3):137-141. (in Chinese)

[4] 裘进浩, 陈海荣, 陈远晟, 等. 压电驱动器的非对称迟滞模型[J]. 纳米技术与精密工程, 2012,10(3):189-197.

Qiu Jinhao, Chen Hairong, Chen Yuansheng, et al. A model for asymmetric hysteresis of piezoelectric actuators[J]. Nanotechnology and Precision Engineering, 2012,10(3):189-197. (in Chinese)

[5] Ge P, Jouaneh M. Tracking control of a piezoceramic actuator[J]. IEEE Transactions on Control Systems Technology, 1996,4(3):209-216.

[6] Song G, Zhao Jinqiang, Zhou Xiaoqin, et al. Tracking control of a piezoceramic actuator with hysteresis compensation using inverse Preisach model[J]. Mechatronics, IEEE/ASME Transactions on Mechatronics, 2005, 10(2): 198-209.

[7] Ang W T, Khosla P K, Riviere C N. Feedforward controller with inverse rate-dependent model for piezoelectric actuators in trajectory-tracking applications[J]. Mechatronics, IEEE/ASME Transactions on Mechatronics, 2007,12(2):134-142.

[8] Juhász L, Maas J, Borovac B. Parameter identification and hysteresis compensation of embedded piezoelectric stack actuators[J]. Mechatronics, 2011,21(1):329-338.

[9] Jiang Hao, Ji Hongli, Qiu Jinhao, et al. A modified prandtl-ishlinskii model for modeling asymmetric hysteresis of piezoelectric actuators[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2010,57(5):1200-1210.

[10]陈辉, 谭永红, 周杏鹏, 等. 压电陶瓷执行器的动态模型辨识与控制[J]. 光学精密工程, 2012, 20(1):88-95.

Chen Hui, Tan Yonghong, Zhou Xxingpeng, et al. Identification and control of dynamic modeling for piezoceramic actuator[J]. Optics and Precision Engineering, 2012,20(1):88-95. (in Chinese)

[11]王贞艳, 张臻, 周克敏, 等. 压电作动器的动态迟滞建模与H∞鲁棒控制[J]. 控制理论与应用,2014,31(1):35-41.

Wang Zhenyan, Zhang Zhen, Zhou Kemin, et al. Dynamic hysteresis modeling and H-infinity robust control of piezoelectric actuators[J]. Control Theory & Applications, 2014,31(1):35-41. (in Chinese)

[12]彭超,徐红兵,张健.扫描探针显微镜的控制技术综述[J].控制理论与应用, 2011,28(3):285-293.

Peng Chao, Xu Hongbing, Zhang Jian. Control technologies for scanning probe microscope—a review[J]. Control Theory & Applications, 2011,28(3):285-293. (in Chinese)

[13]Goldfarb M, Celanovic N. Modeling piezoelectric stack actuators for control of micromanipulation[J]. IEEE Control Systems, 1997,17(3):69-79.

[14]陈远晟.压电驱动器的迟滞非线性建模与控制[D].南京：南京航空航天大学, 2013.

[15]Badel A, Qiu J, Nakano T. A new simple asymmetric hysteresis operator and its application to inverse control of piezoelectric actuators[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2008, 55(5): 1086-1094.

[16]Chen Y, Qiu J, Palacios J, et al. Tracking control of piezoelectric stack actuator using modified Prandtl-Ishlinskii model[J]. Journal of Intelligent Material Systems and Structures, 2012, 24(6):753-760.

[17]Müller A D, Müller F, Hietschold M, et al. Characterization of electrochemically etched tungsten tips for scanning tunneling microscopy[J]. Review of Scientific Instruments, 1999,70(10):3970-3972.

[18]Cavallini M, Biscarini F. Electrochemically etched nickel tips for spin polarized scanning tunneling microscopy[J]. Review of Scientific Instruments, 2000,71(12):4457-4460.

[19]黄强先,高桥健,初泽毅.基于电化学研磨的 SPM 钨探针制备方法研究[J]. 仪器仪表学报,2005,26(3):258-263.

Huang Qiangxian, Ken Takahashi, Hatsuzawa Takeshi. Research on preparation m ethods of tungsten probe for spm based on electrochem ical pol ish ing[J]. Chinese Journal of Scientific Instrument, 2005, 26(3): 258-263. (in Chinese)

[20]王卫勋. 微电流检测方法的研究[D]. 西安: 西安理工大学, 2007.

*国家重点基础研究发展计划(“九七三”计划)资助项目(2015CB057501)；国家自然科学基金资助项目(11372133&51405235);中央高校基本科研业务费专项资金资助项目(NE2015001&NE2015101)；中国博士后特别资助项目(2014T70514)；江苏省基金重点资助项目(BK20150061);江苏高校优势学科建设工程资助项目

2015-05-15；

2015-06-10

10.16450/j.cnki.issn.1004-6801.2017.02.002

TP271; TH702

季宏丽，女，1983年2月生，博士、副教授、硕士生导师。主要研究方向为智能材料与结构，包括高性能压电材料与器件、结构的振动与噪声控制、流动控制、健康监测、能量回收、自适应结构、压电器件的精密传感与驱动技术等。曾发表《基TMS320F2812的悬臂梁振动半主动控制》(《光学精密工程》2009年第17卷第1期)等论文。 E-mail: jihongli@nuaa.edu.cn