Significant intervals of energy transforms in bubbles freely oscillating in liquids＊

Karel Vokurka

Physics Department, Technical University of Liberec, Liberec, Czech Republic, E-mail: karel.vokurka@tul.cz

Significant intervals of energy transforms in bubbles freely oscillating in liquids＊

Karel Vokurka

Physics Department, Technical University of Liberec, Liberec, Czech Republic, E-mail: karel.vokurka@tul.cz

A wall motion of a bubble freely oscillating in a liquid is studied from the point of view of energy conversions at different instants. It is shown that the time of the bubble oscillation can be divided into two distinct intervals. In the first long interval (here called PK and KP intervals) the prevailing energy conversion is between the potential energy of the bubble and the kinetic energy of the liquid. In the second short interval (here called KI and IK intervals) the kinetic energy of the liquid is transformed into the internal energy of the gas/vapor in the bubble interior and into some other forms of energy. By observing the bubble wall motion in the PK and KP intervals, it is shown that only the value of the maximum bubble radius in the corresponding oscillation can be determined. However, only the knowledge of the maximum bubble radii is insufficient for formulation of a correct theoretical model. Unfortunately this fact is often not noticed in the literature.

Energy transforms, free bubble oscillations, energy conversions in bubbles

Introduction

Bubble oscillations remain an important topic in fluid dynamics. While they are traditionally associated with erosion damage[1-5], recent efforts are aiming at medical applications, such as contrast-enhancing in ultrasonic imaging[6-9]and shock wave lithotripsy[10,11]. More recent studies are aiming at seismic airgun development[12-14], acoustic emission monitoring[15], bubble augmented waterjet propulsion[16], effects of liquid compressibility[17], microbubble dynamics monitoring[18], standing cavitation bubbles generation[19], and optimization of an augmented Prosperetti-Lezzi model[20]. In experimental studies of free bubble oscillations both spark generated bubbles[1,21-25]and laser generated bubbles[2,3,26-33]represent very useful tools.

In spite of many works dealing with physics of bubble oscillations (Ref.[34] is a recent extensive review of this topic), there still remain many unanswered questions. One important point concerns energy transforms in oscillating bubbles. Analyses of energy transforms either theoretical, or even based on experimental data, are rare in literature and an analysis of energy transforms encompassing different time intervals is missing completely. This has serious consequences. For example, when reviewing the literature it can be seen that many authors fit their experimental radius vs. time data with theoretical variations computed using models based on the assumption of an ideal gas bubble oscillating adiabatically. After selecting a suitable intensity of the bubble oscillation the correspondence over a relatively large part of the time of the bubble oscillation can be obtained. The theoretical model is thus considered to be validated and is further used to compute, e.g., pressure and temperature in the bubble at its maximum contraction. As will be shown, such an approach, which at first sight might seem to be correct, leads to incorrect results.

1. Experiment vs. theory

As an introduction to the following discussion, selected experimental results are compared with theoretical ones in this section. The experimental data have been obtained when studying the spark generated bubbles. These bubbles have been produced by discharging a capacitor bank via a sparker submerged in a laboratory water tank having dimensions of 6 m (length)×4 m (width)×5.5 m (depth). The sparker electrodes have been made of tungsten wires of diameter 1 mm and the gap between the two electrodes has been set at approximately 1 mm. The sparker has been positioned at a depth of 2.5 m with a distance to thenearest water tank wall of 1.2 m. The capacitance of the capacitor bank could be varied in steps by connecting 1 to 10 capacitors in parallel. Each of these capacitors had a capacitance of 40 mF. The capacitors have been charged with a high voltage source whose voltage could be varied from 2.0 kV to 2.5 kV. An air-gap switch has been used to trigger the discharge through the sparker.

Fig.1 (Color online) Selected frames from a high-speed camera record. The bubble size is, the intensity of bubble oscillation is, the framing rate is 2 800 fps. The time at each frame refers to the time scale origin, which has been selected to coincide with a time, when the bubble attains the maximum radius(see also Fig.2). At the sides of the bubble two conical brass holders of the tungsten electrodes can be seen. The tungsten electrodes themselves can be seen penetrating into the bubble. Small bright objects with tube like traces moving outside the bubble are plasma packets. The two bright objects at the sides of the frames are illuminating lamps

Both the spark discharge and subsequent bubble oscillations are accompanied by intensive optical and acoustic radiations. These radiations have been monitored by a broadband hydrophone and an optical detector. A limited number of high-speed camera records have also been taken with framing rates ranging from 2 800 to 3 000 fps (frames/second). A more detailed description of the experimental setup can be found in Refs.[35-37].

The size of the bubbles studied in these experiments is described by the first maximum radiusand the bubble oscillation intensity is described by the non-dimensional peak pressure in the first acoustic pulseis the peak pressure in the first acoustic pulsethat has been radiated by the bubble during its first contraction,is the ambient (hydrostatic) pressure at the place of the sparker, andis the hydrophone distance from the sparker center.

In the following the results from one particular experiment will be described. In this experiment the bubble size was, the hydrophone distance from the sparker center wasand the intensity of this bubble oscillation, as determined from the pressure record, was. Selected frames from a film record obtained by a high-speed camera are displayed in Fig.1. In these frames the bubble is shown at different instants during the first contraction phase. Throughout this paper this bubble will be used as a reference.

The bubble radii corresponding to different instants can be determined from the frames. Values of the bubble radii obtained in this way are displayed in Fig.2. As the experimental bubble is not ideally spherical (it is slightly elongated in a vertical direction), the data points represent an average from two perpendicular directions (horizontal and vertical). The time interval between two points is given by the framing rate of the camera.

In Fig.2 the experimental points are plotted together with theoretical variations of the bubble radiusThe theoretical variations have been computed using four different bubble models. One of these theoretical curves has been obtained under assu-mption of a non-compressible liquid (that is, using the Rayleighʼs model[38]). The remaining three curves have been computed under assumption of liquid compressibility using the Gilmoreʼs, Herringʼs, and Herringʼs modified model[38]. In all theoretical models a spherical gas bubble oscillating adiabatically has been assumed. The constants used in these computations had the values corresponding to the experimental conditions: the ambient pressure, liquid density, velocity of sound in the liquid, the ratio of the specific heats of the gas in the bubble, constants in the Tait equation of state for the liquidthe bubble size, and the non-linear amplitude of the first bubble oscillation(the non-linear amplitude is defined aswhereis an “equilibrium” radius). The value ofhas been determined from the experimental value ofusing the theoretical scaling functionand the procedure described in Ref.[36].

Fig.2 Comparison between experimental data and theoretical variations of the bubble radiusRwith timetduring the first contraction phase (experimental data for the following expansion phase originating from the same experiment are shown in Fig.4). The time scale origin has been selected as an instant when the theoretical computations start, i.e., when the bubble radius isand the bubble wall velocityThe experimental points have then been shifted along the time scale until the best agreement with the theoretical curves has been obtained. The position of the first data point then determines a time reference for the remaining experimental points. The final stages of the bubble contraction are shown enlarged in the inset. Letters HM, R, H, and G stand for Herring’s modified, Rayleighʼs, Herringʼs, and Gilmoreʼs models respectively

As can be seen in Fig.2 at first sight, all theoretical models yield a reasonable fit to the experimental points. Even more, the curves corresponding to different theoretical models are almost indistinguishable mutually in the scales used in Fig.2. The overall shapes of the theoretical curvesresemble an “inverted tea cup” (in Fig.2 only a half of this “cup” is displayed), and from what has been said it follows that this shape is independent of the form of the equations used to approximate the liquid compressibility. Or, in other words, it is independent of the theoretical model used in computations. The theoretical curves start to differ from each other only at the final stages of the bubble contraction (shown enlarged in the inset), where, unfortunately, no experimental points are available for comparison. To explain this relative independence of thecurve shape on the liquid compressibility, the transforms of energy in a freely oscillating bubble must be analyzed. This will be done in the following Section.

2. Intervals of energy transform

In the experiments described in Section 1 the spark generated bubbles have been studied. As it has been shown earlier by analyzing the radiated pressure waves[39], the spark generated bubbles are basically vapor bubbles (that is, except that the bubble contains a limited amount of gases, the vapor evaporation and condensation at the bubble wall play an important role for them), they do not behave adiabatically[37], and their oscillations are accompanied by certain energy transforms, character of which is still not very well understood[35-37]. At present time there is no theoretical model available in the literature taking into account all these features. Therefore Herringʼs modified model will be used here. This model has an advantage in a relatively high acoustic radiation and is relatively simple so that the analysis is more transparent. It will be shown later that this model meets the expectations of its role in this paper well.

The model assumes a spherical gas bubble freely oscillating in a compressible and extended liquid. The thermal behavior of the bubble is assumed to be adiabatic. The excitation of the bubble for free oscillation is assumed to be done by initially decreasing its energy. The analysis will be limited to the first contraction and expansion phases. It will be shown that even if this simple model is used to represent a real spark generated bubble, a useful insight into the transforms of energies can be obtained.

Consider a spherical gas bubble of radiusand let the bubble be initially at rest. At the momentthe pressure of the gas in the bubble interior is instantaneously decreased to a value. Due to the excess pressure,, the bubble will start contracting to a first minimum radius(the first contraction phase lastingand then will expandto a second maximum radius(the first expansion phase lasting

The initial potential energy of the bubble is

The liquid, which was initially at rest, is streaming towards the bubble during the contraction phase and acquires a kinetic energy

where the dot denotes time differentiation.

As said above, during the bubble contraction and expansion the gas pressure,P, is supposed to change according to the adiabatic law

The initial internal energy of the gas (referred to an infinite expansion of the bubble, at which the internal energy is defined to be zero) is

The work done on the gas during the compression fromwill manifest itself as the increase of the internal energy

The oscillation of this bubble is governed by the energy relation

In Eq.(8) the bubble oscillation intensity is determined by the ratio of the initial pressureto the ambient pressure that is byHowever, as shown in Ref.[39], in theoretical computations a more convenient intensity measure is the nonlinear amplitude of the first oscillationThe “equilibrium” radiusused in computingis defined by a condition thatAnother measure of the bubble oscillation intensity, convenient above all in experimental works, is the non-dimensional peak pressure in the first acoustic pulse,introduced already in Section 1.

As said above, in this work the Herringʼs modified Eq.(8) has been selected for two reasons. First, it is a relatively simple equation. However, the second reason is even more important. As has been shown in many experiments with spark and laser generated bubbles, cavitation bubbles and bubbles generated by underwater chemical explosions, oscillations of real bubbles are strongly damped. At present, unfortunately, some energy transforms, which are responsible for this damping, are not sufficiently known[3,26,35-37,39]. Thus a significant part of the damping, because its nature is not known, is not taken into account in any theoretical computations published in literature. The unknown energy transforms certainly limit the validity of any present theoretical model and thus the results obtained with any model have to be interpreted with extreme caution. Herringʼs modified equation, when compared with Gilmoreʼs equation, gives a stronger acoustic radiation, and such a stronger acoustic radiation may be used to cover a part of the unknown energy losses. Thus for the same intensity of oscillations Herringʼs modified equation gives less extreme results, which seems to be closer to reality than the results obtained for the same initial intensity with Gilmoreʼs equation.

An example of computed variations of energieswith timetis given in Fig.3. The variations shown in Fig.3 are a graphicalrepresentation of Eq.(7) and thusrepresents a decrease ofan increase ofFor convenience the energies are displayed in a normalized form defined asWhen solving Eqs.(2), (3), (6), and (8) the values of physical constants and of other parameters given in Section 1 have been used.

Fig.3 Variations of the normalized energiesandwith timetin the first contraction (compression) and expansion phases. The contraction phase is lastingthe expansion phase is lastingTime scale origin was set to coincide with the beginning of the contraction phase.is a normalized bubble radius andis an instant, when the kinetic energyattains a maximum value

As can be seen in Fig.3 the transform of the bubble potential energy into the kinetic energy of the liquid is dominating during almost 97% of the contraction phase. The transform of the potential energy into the internal energy of the gas or into the radiated acoustic energy is not significant in this interval. And as follows from Eqs.(2)-(3), both the potential and kinetic energies are independent of the liquid compressibility. Thus in this interval the bubble wall motion is almost independent of the liquid compressibility and of any thermodynamic processes in the bubble or at the bubble wall. It follows then that the motion of the wall of any real bubble is well modeled by the present theory in this interval.

It does not mean that the thermodynamic processes in this interval play no role in the bubble wall motion. However, these processes will manifest themselves significantly only during the last 3% of the contraction phase. In other words, the processes that take place in the bubble and at the bubble wall in this interval are accumulating their effects to show them in full strength just in the last few moments of the bubble contraction, lasting only about 3% of the contraction phase. Only in these last instants an important information can be obtained (e.g., by observing the bubble wall motion) regarding the processes occurring in the whole contraction phase. And only such information can then serve as a solid base when defining a correct mathematical model of the real bubble.

In the last moments of the contraction phase, when the kinetic energy and partially also the remaining part of the potential energy are being intensively transformed into the internal energy of the gas, a part of these energies is being dissipated as the acoustic energy in the theoretical model. However, analysis of the experimental data shows[3,26,35-37,39]that in the real bubble a part of the potential and kinetic energy is dissipated not only as the acoustic energy, but also by some further, yet unknown processes. Therefore any further computation at the final stages of the bubble contraction and in the following expansion phase must be done (and interpreted) with utmost care, because the present theoretical model begins to depart from reality significantly.

Hence, if the computation continues further beyond the first contraction phase that is in the first expansion phase, a picture similar to that obtained above can be seen again. Now the flow of the energies is inverted. The energy accumulated in the gas as the internal energy is transformed extremely fast mainly into the kinetic energy of the liquid (now the liquid is streaming outwards away from the bubble), partially also into the potential energy of the bubble. In the theoretical model it is also partially dissipated as the acoustic energy, whereas in a real bubble it is dissipated as the acoustic energy and also (as already mentioned above) by some yet unknown processes. These initial transforms will last about 3% of the first expansion phase again. However, because a large part of the energies has been dissipated in the vicinity of the minimum radius, the magnitude of the kinetic and potential energies will be smaller now (see Fig.3). At the end of this short interval the kinetic energy attains a maximum value and in the following long interval, lasting about 97% of the expansion phase, this kinetic energy and the remaining part of the internal energy are being transformed back into the potential energy of the bubble. And again, the energy transforms in this long interval are independent of the liquid compressibility and of the thermodynamic processes in the bubble and at the bubble wall. Resulting form of the radius vs. time curve will be the same as in the case of the first oscillation. However, now the size of thecurve (characterized by the value of) will be smaller, because a large part of the energies has been dissipated during the bubble wall motion in the vicinity of the minimum radius(see Fig.4).

From what has been said (and what can be seen in Fig.3) it follows that both the contraction and expansion phases can be divided into two distinct intervals. The first interval, which includes about 97% of each phase, in which the governing energy trans-form is between the potential and kinetic energy, and the second interval, which includes about 3% of each phase, in which the governing energy transform is between the kinetic and internal energy. And in this short second interval a large part of the internal energy is dissipated as the acoustic energy (in the theoretical model) or as the acoustic energy and some other experimentally yet not sufficiently studied energies.

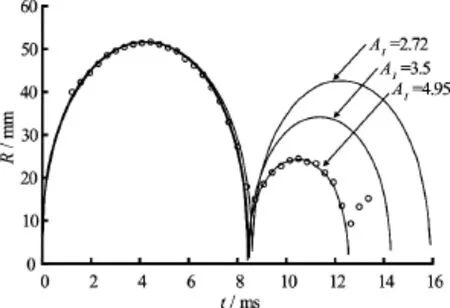
Fig.4 Fitting the experimental data with theoretical curves computed for different bubble oscillation intensities. The time scale origin is set at the beginning of the growth phase. The experimental data originate from the same experiment as those shown in Fig.2. However, now all the experimental data available both for the first growth phase, the first contraction phase and the second and third oscillations are displayed. The theoretical variations ofhave been computed with Herringʼs modified model starting atand the growth phases have been obtained by inverting the first contraction phases. The physical constants and parameters used in computations are given in Section 1

With respect to the governing energy transforms the first large interval can be called the PK interval (“potential-kinetic” interval), and the second short interval can be called the KI interval (“kineticinternal” interval). In these abbreviations the acoustic energy has been omitted for the sake of simplicity.

It follows from the previous discussion that the shape of thecurve is determined in the PK interval. The previous discussion also explains why this shape is independent of the liquid compressibility and of the thermodynamic processes in the bubble and at the bubble wall. On the other hand all important thermodynamic and dissipative processes will manifests their effects in the KI interval.

An instant the kinetic energy attains the maximum value will be denotedand it can be used as a suitable boundary point between the PK and KI intervals (see also Fig.3). The extent of the KI interval is thenand it may be convenient to express this extent as a percentage of the contraction phase duration, that is as. It is evident that the value ofalso depends on the bubble oscillation intensity. Thus for(medium intensity oscillations) is obtainedis obtained(high intensity oscillations) is obtained. These values ofhave been computed with the bubble model described above.

It is possible to define similar intervals as above for the first expansion phase as well. One will obtain the IK (“internal-kinetic”) and KP (“kinetic-potential”) intervals now.

The discussion of the energy transforms in a freely oscillating bubble just presented also explains why the value ofis only very weakly dependent on the bubble oscillation intensity, liquid compressibility, the thermodynamic processes in the bubble interior and at the bubble wall (e.g., whether the bubble interior contains gas or vapor), and on the dissipative processes accompanying the bubble oscillations. In other words, the discussion reveals whydetermined in the classical Rayleighʼs model of an empty bubble fits so well the experimental data, and also why, when measuring in experiments only, not much can be learned about the observed bubble.

3. Discussion

In Sections 1 and 2 it has been shown that by observing the bubble wall motion in the PK and KP intervals nothing significant can be obtained about the bubble (with the exception of the maximum radiiIn case of bubbles oscillating sufficiently intensively, the shape of the curvesin the first and second oscillations, apart from the size, is almost the same. This is true for both the gas and vapor bubbles, that is, not only for spark and laser generated bubbles, but also for cavitation bubbles (generated both in hydrodynamic and acoustic cavitation) and for bubbles generated by underwater chemical explosions. By observing this shape no conclusion about liquid evaporation or vapor condensation, gas diffusion, heat conduction, etc., can be made. If the bubble oscillation intensity is specified properly, all bubble models commonly used (Rayleighʼs, Herringʼs, Herringʼs modified, Gilmoreʼs, etc.) yield almost the same variation of the bubble radius with time in these intervals (see Fig.2). This very good fitting of all bubble models to the experimental data testifies that any unaccounted for process in the PK and KP intervals has a negligible effect on the shape of thecurve. If the intention is to learn more about the bubble or to verify the validity of a theoretical model, then the bubble wall motion must be observed in the KI and IK intervals first of all and the study of the wall motion must always beaccompanied by investigation of other processes (such as the acoustic and optical radiations from the bubble) as well.

So far, only a limited number of “probes” into the IK and KI intervals have been reported in the literature[27,28]. Since the knowledge of bubble behavior in the IK and KI intervals is severely limited at present, it cannot be decided by comparing the experiments with theory which mathematical model (Gilmoreʼs, Herringʼs, etc.) gives the best results. Therefore at present time it is rather irrelevant which bubble model is used for the analysis. This is also one of the reasons why the Herringʼs modified model is used in this work.

As said above, for bubbles oscillating sufficiently intensively the shape of the radius vs. time curves will always be the “inverted tea cup”, both in the first and second bubble oscillation. The size of thecurve in the first oscillation will be determined by the energy available for the growth phase minus energy dissipated at the initial instant of the bubble growth (the growth phase of spark generated bubbles has not been discussed in this paper). The size of thecurve in the second oscillation will depend on the energies remaining from the first oscillation after the dissipated energies are subtracted. Thus in the graphical presentation of the first and second bubble oscillations there are always two “inverted tea cups” next to each other. First, a larger “cup” corresponding to the first bubble oscillation, followed by a smalle “cup” corresponding to the second bubble oscillation (for the sake of brevity further bubble oscillations are omitted from the discussion). How small the second “cup” is, as compared with the first one depends on the energy dissipated in the KI and IK intervals first of all. However, it follows from the results presented in Section 2 that as far as the shape of thecurve and its size are concerned, the nature of the dissipative mechanism (whether it is the acoustic radiation, thermal radiation, heat conduction, liquid evaporation, vapor condensation, etc.) plays no role. As can be verified in literature, this fact is very often ignored and this leads to misinterpretation of the measured data.

Because at present the role of the different dissipative processes has not been clarified yet (and thus these processes cannot be included in the respective theoretical models correctly), some researchers try to fit the size of thecurve in the second oscillation by using the dissipative mechanisms already known. These are, first of all, the acoustic radiation, and in the case of smaller bubbles also the viscous losses (which are unimportant for the large bubbles considered here). The amount of the radiated acoustic energy increases with the bubble oscillation intensity. Thus by increasing the bubble oscillation intensitysufficiently, the required cumulative dissipated energy can be obtained and thus also the required fit to the experimentally determined size of thecurve in the second oscillation can be achieved. Such a procedure is shown in Fig.4.

To illustrate possible pitfalls arising from using the excessive bubble oscillation intensities, let us have a look at the densityof the gas in a theoretical bubble. Assuming the conservation of the mass in an ideal gas bubble (such assumption is implicitly present in Eq.(4)) it follows thatis the gas density at the equilibrium radiusis the gas density at the first minimum radius. This equation can be rearranged easily to yieldFor the given amplitudethe value ofcan be computed using, e.g., the Herringʼs modified model. Thus for a bubble oscillating with the amplitude(this is the intensity of oscillation determined fromearlier) one obtainsAssuming further that(approximately the density of saturated vapor at the pressure100 kPa and temperature3 189 kg/m. For(this is the bubble oscillation intensity used in Fig.4 to fit the experimental data both in the contraction and expansion phases) one obtains, and hence. However, if the computation is done with Gilmoreʼs model as it is common in the literature, then to obtain a fit to the second maximum bubble radius, the bubble oscillation intensity must be increased from(Gilmoreʼsmodel radiates acoustically less intensively than Herringʼs modified model and therefore higheris needed now). In this case the corresponding value of the non-dimensional minimum radius isand the density is. Let us remind here that the highest densities of solids given in physical tables are approximately(e.g., for tungsten). To emphasize the fact that the computed values ofare physically unrealistic, the signs “almost equal to”have been used here.

It can be seen immediately that the value ofobtained with the Gilmore’s model is unrealistically high from the physical point of view. However, when reviewing the literature on bubble oscillations, numerous examples of computations can be found where the authors use similar extremely high values of bubble oscillation intensity in order to obtain the required fit to the experimental data (this approach has been used by Lauterborn and his students first[34], and it is extensively used in theoretical computations on bubbles oscillating in acoustic resonators nowadays). Such a procedure is possible because from the mathematical point of view there is no limit on the theoretical bubble oscillation intensity. To solve the problem concerning these excessive gas densities, some authors have been considering the so-called van der Waals hard core. However, this is a cosmetic procedure only, which cannot overcome the physical incorrectness caused by not considering all dissipative processes existing in a bubble. In real bubbles these dissipative processes “soften” the bubble oscillations significantly so that the usage of van der Waals core in theoretical computations is then most probably unnecessary (see the value ofcomputed above for the intensity of oscillation

4. Conclusions

At the beginning of Section 2 a number of simplifying assumptions have been made. These assumptions concerned, e.g., the liquid compressibility, the thermal behavior of the bubble, and the method of the bubble excitation for free oscillation. In the following analysis it has been verified that in the PK and KP intervals these assumptions play, if any, only a minor role. However, in the KI and IK intervals these assumptions cannot be used. Nevertheless, the analysis in the KI and IK intervals has been purposefully limited to a minimum, with the exception of a few points discussed in Section 3.

It has been shown that by observing the bubble wall motion in the PK and KP intervals only, not much information about the processes in a bubble can be obtained. This fact certainly represents a serious limit regarding the correct formulation of a bubble model. Thus it is not possible to agree with the authors of the recent review paper[34], who claim that “a remarkable agreement can be obtained” between experimental points and theoretical computations based on Keller-Miksis model (cf. a remark at Fig.38 of Ref.[34]). In this case the theoretical bubble oscillates with the amplitude(the nomenclature used in Ref.[34] forhas been adopted here). As far as the densityat such high oscillation intensities is concerned, we refer to the numerical examples given in Section 3. Unfortunately, similar procedures, which are based on using excessive and unrealistic intensities of bubble oscillation, are very common in literature.

It is our opinion that to obtain a better understanding of the bubble behavior a lot of work still must be done. New experiments should concentrate on the bubble wall motion in the KI and IK intervals first of all. For example, it is already known that the bubble shape at the final stages of the contraction phase is not spherical[27,28]. However, no further details of this shape are known. And the observations of the bubble wall motion must always be accompanied by measurements of the acoustic and optical radiation and by studying other processes as well. This is a very challenging task. However, no further progress in the correct understanding of bubble oscillations can be obtained without completing this task.

Acknowledgements

This work was supported by the Ministry of Education of the Czech Republic (Research Grant No. MSM 245100304). The author also wishes to thank Dr. Silvano Buogo from the Italian Acoustics Institute, CNR, Rome, Italy, for a very valuable help with taking the high-speed camera records.

[1] Jayaprakash A., Hsiao C.-T., Chahine G. Numerical and experimental study of the interaction of a spark-generated bubble and a vertical wall [J].Journal of Fluid Engineering, 2012, 134(3): 031301.

[2] Shaw S. J., Schiffers W. P., Emmony D. C. Experimental observation of the stress experienced by a solid surface when a laser-created bubble oscillates in its vicinity [J].Journal of the Acoustical Society of America, 2001, 110(4): 1822-1827.

[3] Isselin J.-C., Alloncle A.-P., Autric M. On laser induced single bubble near a solid boundary: Contribution to the understanding of erosion phenomena [J].Journal of Applied Physics, 1998, 84(10): 5766-5771.

[4] Wang Q. X., Yang Y. X., Tan D. S. et al. Non-spherical multi-oscillations of a bubble in a compressible liquid [J].Journal of Hydrodynamics, 2014, 26(6): 848-855.

[5] Yang Y. X., Wang Q. X., Keat T. S. Dynamic features of a laser-induced cavitation bubble near a solid boundary [J].Ultrasonics Sonochemistry, 2013, 20(4): 1098-1103.

[6] Sboros V. Response of contrast agents to ultrasound [J].Advanced Drug Delivery Reviews, 2008, 60(10): 1117-1136.

[7] Stride E. P., Coussios C. C. Cavitation and contrast: The use of bubbles in ultrasound imaging and therapy [J].Proceedings of the Institution of Mechanical Engineers Part H-Journal of Engineering in Medicine, 2010, 224(42): 171-191.

[8] Thomas D. H., Butler M., Pelekasis N. et al. The acoustic signature of decaying resonant phospholipid microbubbles [J].Physics in Medicine and Biology, 2013, 58(3): 589-599.

[9] Faez T., Emmer M., Kooiman K. et al. 20 years of ultrasound contrast agent modeling [J].IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2013, 60(1): 7-20.

[10] Leighton T. G., Turangan C. K., Jamaluddin A. R. et al. Prediction of far-field acoustic emissions from cavitation clouds during shock wave lithotripsy for development of a clinical device [J].Proceedings of the Royal Society A-Mathematical Physical and Engineering Sciences, 2013, 469(2165): 20120538.

[11] Kang G., Cho S. C., Coleman A. J. et al. Characterization of the shock pulse-induced cavitation bubble activities recorded by an optical fiber hydrophone [J].Journal of the Acoustical Society of America, 2014, 135(3): 1139-1148.

[12] De Graaf K. L., Brandner P. A., Penesis I. Bubble dynamics of a seismic airgun [J].Experimental Thermal and Fluid Science, 2014, 55: 228-238.

[13] De Graaf K. L., Brandner P. A., Penesis I. The pressure field generated by a seismic airgun [J].Experimental Thermal and Fluid Science, 2014, 55: 239-249.

[14] De Graaf K. L., Penesis I., Brandner P. A. Modelling of seismic airgun bubble dynamics and pressure field using the Gilmore equation with additional damping factors [J].Ocean Engineering, 2014, 76: 32-39.

[15] Husin S., Addali A., Mba D. Observation of acoustic emission from gas bubble inception and burst [J].Proceedings of the Institution of Mechanical Engineers Part E-Journal of Process Mechanical Engineering, 2012, 226(E1): 79-78.

[16] Wu X., Choi J.-K., Singh S. et al. Experimental and numerical investigation of bubble augmented waterjet propulsion [J].Journal of Hydrodynamics, 2012, 24(5): 635-647.

[17] Zhang Y. N., Li S. C. Effects of liquid compressibility on radial oscillations of gas bubbles in liquids [J].Journal of Hydrodynamics, 2012, 24(5): 760-766.

[18] Fouan D., Achaoui Y., Payan C. et al. Microbubble dynamics monitoring using a dual modulation method [J].Journal of the Acoustical Society of America, 2015, 137(2): EL144-EL150.

[19] Iwata Y., Takada N., Sasaki K. A simple method for efficient generation of standing cavitation bubbles [J].Applied Physics Express, 2013, 6(12): 127301.

[20] Geers T. L. Optimization of an augmented Prosperetti-Lezzi bubble model [J].Journal of the Acoustical Society of America, 2014, 136(1): 30-36.

[21] Buogo S., Cannelli G. B. Implosion of an underwater spark-generated bubble and acoustic energy evaluation using the Rayleigh model [J].Journal of the Acoustical Society of America, 2002, 111(9): 2594-2600.

[22] Krieger J. R., Chahine G. L. Acoustic signals of underwater explosions near surfaces [J].Journal of the Acoustical Society of America, 2005, 118(5): 2961-2974.

[23] Khoo B. C., Adikhari D., Fong S. W. et al. Multiple sparkgenerated bubble interactions [J].Modern Physics Letters B, 2009, 23(3): 229-232.

[24] Fong S. W., Adhikari D., Klaseboer E. et al. Interactions of multiple spark-generated bubbles with phase differences [J].Experiments in Fluids, 2009, 46(4): 705-724.

[25] Huang Y., Yan H., Wang B. et al. The electro-acoustic transition process of pulsed corona discharge in conductive water [J].Journal of Physics D: Applied Physics, 2014, 47(25): 255204.

[26] Ward B., Emmony D. C. Interferometric studies of the pressures developed in a liquid during infrared-laser-induced cavitation-bubble oscillation [J].Infrared Physics, 1991, 32(91): 489-515.

[27] Baghdassarian O., Chu H.-C., Tabbert B. et al. Spectrum of luminescence from laser-created bubbles in water[J].Physical Review Letters, 2001, 86(21): 4934-4937.

[28] Lindau O. Investigation of laser generated cavitation (Untersuchungen zur lasererzeugten kavitation) [D]. Doctoral Thesis, Göttingen, Germany: Universität Göttingen, 2001(in German).

[29] Gregorčič P., Jezeršek M., Možina J. Optodynamic energy-conversion efficiency during an Er: YAG-laser-pulse delivery into a liquid through different fiber-tip geometries [J].Journal of Biomedical Optics, 2012, 17(7): 075006.

[30] Obreschkow D., Tinguely M., Dorsaz N. et al. The quest for the most spherical bubble: experimental setup and data overview [J].Experiments in Fluids, 2013, 54(4): 1-18.

[31] Hegedüs F., Koch S., Garen W. et al. The effect of high viscosity on compressible and incompressible Rayleigh-Plesset-type bubble models [J].International Journal of Heat and Fluid Flow, 2013, 42(4): 200-208.

[32] Bulanov A.V., Nagornyi I. G., Sosedko E. V. Specific features of the acoustic emission upon the optical breakdown in liquid induced by the radiation of Nd: YAG laser [J].Technical Physics, 2013, 58(8): 1201-1204.

[33] Sato T., Tinguely M., Oizumi M. et al. Evidence for hydrogen generation in laser- or spark-induced cavitation bubbles [J].Applied Physics Letters, 2013, 102(7): 074105.

[34] Lauterborn W., Kurz T. Physics of bubble oscillations [J].Reports on Progress in Physics, 2010, 73(10): 106501.

[35] Buogo S., Plocek J., Vokurka K. Efficiency of energy conversion in underwater spark discharges and associated bubble oscillations: Experimental results [J].Acta Acustica united with Acustica, 2009, 95(1): 46-59.

[36] Buogo S., Vokurka K. Intensity of oscillation of sparkgenerated bubbles [J].Journal of Sound and Vibrations, 2010, 329(20): 4266-4278.

[37] Vokurka K., Plocek J. Experimental study of the thermal behavior of spark generated bubbles in water [J].Experimental Thermal and Fluid Science, 2013, 51(1): 84-93.

[38] Vokurka K. Comparison of Rayleighʼs, Herringʼs, and Gilmoreʼs models of gas bubbles [J].Acustica, 1986, 59(3): 214-219.

[39] Vokurka K. Amplitudes of free bubble oscillations in liquids [J].Journal of Sound and Vibration, 1990, 141(2): 259-275.

(Received November 17, 2015, Revised April 19, 2016)

* Biography: Karel Vokurka (1944-), Male, Ph. D., Professor